I released AZdecrypt 1.08 and it has a cool new feature.
We have seen putative period 15/19 solutions that have a score of around 21000 or otherwise have interesting readable fragments that seem to relate to eachother. If the 340 truly is a sequential homophonic substitution + transposition cipher then AZdecrypt 1.08 has a new stat that will us help sort if any of these solutions is really interesting or not. This stat, PC-cycles, measures plaintext to ciphertext cycles and its score should spike if a solution is somewhat close.
Here is an example of such on a cipher by Largo, note that the PC-cycles score is 4181, which is too high to be random, while the AZdecrypt substitution score is only 20813 and the plaintext is not really readable. Anything around the 2000 mark could potentially be interesting and if you happen to find such for the 340 I would love to see them.
Score: 20813.74 Ioc: 0.07076 Ngrams: 442 PC-cycles: 4181 <--- Columnar(19*18,TP,C:3) Offset column order(57*6,X:2) Offset(X:69) TPOINTSTHISROBETH EOLINEESHEDTOLIMI NHECORRONELHGROUN DANDRERBYHITEELEM ISMOUNGAABUTSLIDE LTYINAREEPITSAREE SPEANCARNINAGROMA NNANDHISMONESEALC OSLERATEOUTSINSOU RTICARANPRODUCTOR NEDMSPINGOTANDTHE PHINPRODUCEDMSBAR IPIIBISAIDSTDANED DINALINOLONEHIDEL INHIMESPARESEAPOO RETTOCHATMOTISATL EDAPRAYAPRIESSPEN NESAGOORATTOCLAYM OSANESSEAHANDALBO URATHERATHOMESOMO
Thanks for 1.08. I downloaded it this morning. I have been taking a needed break these last couple of weeks.
Okay smokie,
I am very happy with 2017 so far and divided my cryptology work between the development of AZdecrypt, the 340 and a few other ciphers. For the homophonic substitution + transposition hypothesis we debunked that a reasonable message is divided cleanly over the period 15/19 lines thanks to your row solver concept. My transposition solver has likely debunked all of the simple transpositions that it supports and your statistical debunking of digraph substitution was excellent.
Furthermore, in a homophonic substitution + normal/mirrored/flipped/reversed direction I looked at more than 50 languages, aperiodical polyalphabetism, vigenère and combinations of whole symbol groups acting as nulls. I came up with a solver that merges sequential homophones and looked at encoding nulls. While at the same time making all of this functionality available in AZdecrypt. I have one more AZdecrypt update planned to fix some bugs and probably not much more — time will tell — rest and reinspire for 2018.
Perpetual motion: https://www.youtube.com/watch?v=nifWUdA … A&index=10
Okay smokie,
I am very happy with 2017 so far and divided my cryptology work between the development of AZdecrypt, the 340 and a few other ciphers. For the homophonic substitution + transposition hypothesis we debunked that a reasonable message is divided cleanly over the period 15/19 lines thanks to your row solver concept. My transposition solver has likely debunked all of the simple transpositions that it supports and your statistical debunking of digraph substitution was excellent.
Furthermore, in a homophonic substitution + normal/mirrored/flipped/reversed direction I looked at more than 50 languages, aperiodical polyalphabetism, vigenère and combinations of whole symbol groups acting as nulls. I came up with a solver that merges sequential homophones and looked at encoding nulls. While at the same time making all of this functionality available in AZdecrypt. I have one more AZdecrypt update planned to fix some bugs and probably not much more — time will tell — rest and reinspire for 2018.
Perpetual motion: https://www.youtube.com/watch?v=nifWUdA … A&index=10
I am happy with 2017 as well.
Digraph + transposition + homophonic drives up the average probability score of the bigram repeats because the +/- 63 homophonic symbols are distributed more evenly across all 26 letters of the alphabet, actually the digraph symbols. It is easier to make messages where the bigram repeat count spike and the bigram repeat probability score spike are at the same period with digraph, and that is what we have with the 340. However, untransposing and then checking for odd / even bias does not show any bias. Even when sliding one skip or null. However, that doesn’t consider transposition anomalies such as incomplete inscription rectangles or multiple skips or nulls. I am not convinced that it is digraph or not.
I don’t see why, though, if someone was going to make a transposition + homophonic, realizing that it would be very difficult to detect and solve, given the educational resources available at the time, why they would include another coding step before transposition. The classified military cryptanalysis books of the day discuss transposition, but don’t even discuss detection of inscription shapes at all. So he wouldn’t even know that you could do that and why use digraph. I hope it is just transposition + digraph, but… I don’t know.
You asked me to slide two groups of same configuration as in pivots, both vertical and horizontal. Not much with results except that with the vertical I came up with period 38. I went back to test for accuracy with horizontal . It is not as accurate because of the smaller distortion zone. With vertical *** it is very accurate because of the big distortion zone. So the horizontals could still be nulls. I took them out and there are still a lot of P 15/19. Just a few less.
I am still working on it. We had a lot of ideas, and only touched on a lot of them. I am going back to refine and expand on some of them. I’ll be back.
Hi,
yesterday I’ve worked a bit on z340 and found something interesting. It is based on Doranchaks discovery that shifting the whole cipher one column to the right increases the bigram count at period 19. I wrote a small test that checked the bigram and trigram counts for all combinations of row and column shifts. One of those tests leads to an interesting result:
– Shift the whole cipher one column to the right
– Shift the whole cipher two rows upwards
– Untranspose period 19
– Mirror the cipher
This transposition creates 48 bigrams and 8 trigrams. Unfortunately there is no solve though. What do you think? Is this discovery worth a closer look? Or just a strange coincidence? To me it looks promising.
Jarlve: A lot of my recent experiments created many "ill", "illi" and "illin" fragments. Does AZDecrypt prefer words like "killing"?
KBSnKoFuKFtygc+bJ oH+jsN#FBrNUOubBq TFO4dzgrAYt-1vrN8 cbzpSnO#uXo2dsbh- dC7rtU4+Ghhct+HC5 Egkc+-9VCIwMBE+jW 4+RR-Lme7o+jRaqBm NJ5uKuFFVUkaMtIpa I7chLaPxZObDIqMV0 1Unzg+bGlcHFbQUmI VMjD3OWDdNe+GZt7o +GI4+jWVbh+L7VF7E gke+qYPeWqR-4BTI+ 7jRLmeSnWtg1t4Dd0 bKknIuvCTI+jMYJ+J 5uofZ1u+t+8mB+Zp+ HKLOBWLmrw+bOR2Kw pTwytfxB+30bgkQRy GAYP#uXcBTvFOldzg gIOOCBfGRMnB+8FMS
Interesting find, Largo. There are some interesting repeating patterns in there:

It is based on Doranchaks discovery that shifting the whole cipher one column to the right increases the bigram count at period 19.
This was my find. doranchak found column period 2. I think these bigram peaks are special and possibly/hopefully related to a transposition scheme used in the 340.
This transposition creates 48 bigrams and 8 trigrams. Unfortunately there is no solve though. What do you think? Is this discovery worth a closer look? Or just a strange coincidence?
Very interesting. Need to take a closer look.
Jarlve: A lot of my recent experiments created many "ill", "illi" and "illin" fragments. Does AZDecrypt prefer words like "killing"?
It biases towards the ngrams.
Hi,
sorry Jarlve for my mistake.
I have experimented a little bit and got some interesting results. I don’t want to be presumptuous at this point, but I think that my discovery of the 48 Bigram + 8 Trigrams is the most interesting and promising one in a long time. You’re welcome to correct me, but here are some numbers:
I ran the standard test, which you have used several times for comparisons. z340 is shuffled a total of 10 million times and the number of repeating bigramms and trigrams are counted. Here’s the result:
Results out of 10000000 tests Maximum repeated bigrams: 44 Maximum repeated trigrams: 8 More or equal 37 bigrams: 247 (percentage: 0.00247 %) More or equal 8 trigrams: 1 (percentage: 0.00008 %)
Only in one of 10 million shuffles were 8 trigrams achieved (!!!). 48 bigramms have never (!!!) been reached, the maximum was 44, what looks more than significant to me.
Furthermore, I did other tests where z340 is shifted vertically and horizontally. In one of these tests, 6 "+"-symbols were found next to each other. This didn’t seem to me anything special at first, but here too a random test showed that in 10 million shuffles only in 287 ciphers 6 or more identical symbols in a row showed up.
This result is by far not as significant as the upper one, but it is worth taking a closer look.
I will investigate this further and can only explain the current results as follows: z340 consists of extremely repetitive text. It is possible that two different transpositions are overlapping. For example, one half transposed with scheme A, the second with scheme B. The results were then merged into z340. This leads to spikes, which do not lead to a solution. I think this or a similar idea has already been discussed.
And I still can imagine that the plus-symbols maybe form some pattern when the cipher is transposed in the correct way
– Shift the whole cipher one column to the right
– Shift the whole cipher two rows upwards
– Untranspose period 19
– Mirror the cipher
Largo: Do you mean to move column 17 to column 1, and rows 1 and 2 to rows 19 and 20?
Have you any ideas about a mechanism, a cipher that could cause a transposed message to turn out with columns and rows on the wrong side of the cryptogram? Just wondering.
Here is an example smokie:
Original ipher:
ABCD EFGH IJKL MNOP QRST UVWX
Shift one column to the right:
DABC HEFG LIJK PMNO TQRS XUVW
Shift two rows upwards:
LIJK PMNO TQRS XUVW DABC HEFG
Maybe "rotate" or "roll" would be better terms.
I don’t think this shift/rotation is an effect of a certain kind of a common transposition. I also don’t think that z340 is based on continuous and regular transposition. If I’m not mistaken, the P15/P19 spikes are only partial hits, but they don’t refer to the whole extent of z340. If z340 consists of two mixed transpositions, then the P19 spike could simply be the result of convergence. I find it difficult to put that into words. Imagine that you have two plaintexts of length 170, one transposed with P3, the other with P6, and now the two transposed parts are joined together to form one. Either consecutively or alternately one letter per half. If you look for period spikes in the finished cipher, you will surely find references to P3, because P6 is quasi immament. The basic principle has been discovered, but the solution remains hidden.
My experiment basically does nothing else but a shifted starting point for a P19 transposition. I hoped to discover possible breaks in the transposition method. Maybe that’s exactly what we’re seeing now.
Largo:
I’m glad that you are thinking about transposition. I am about 90% convinced that Zodiac transposed the plaintext before encoding. Old cryptography books show different inscription and transcription shapes, with different routes, etc.
The simplest explanation is that he saw those pictures and made his own variation. Only a few skipped plaintext during transcription, and some gibberish in parts of the message result in an un-solvable jigsaw puzzle even if un-transposed at the correct period.
After that simple explanation, I think that one of the next most simple explanations is that of three shapes. One inscription shape, one intermediate shape, and a final shape of 17 x 20. Here is an example using position numbers instead of a message.
1. Inscribe left right top bottom into a 15 x 22 rectangle.
2. Read top down left right.
3. Transcribe into intermediate shape, another 15 x 22 rectangle, left right top bottom.
4. Decide to do it again just for good measure.
5. Read top down left right.
6. Transcribe left right top bottom into 17 x 20 rectangle.
The result makes what were originally period 2 bigrams in the plaintext into period 19 bigrams, and it is not too difficult to make a message with period 2 predominate, depending on the message and the diffusion. Scroll down to see all three shapes.
There are a lot of possibilities, though. ![]()
Hello!
since I’m running out of ideas for z340 at the moment, I’ve collected lots of statistics. For this purpose I obtained free books from Project Gutenberg, split them into 340-character pieces, encoded them into homophones and then examined them. In the meantime, however, I have felt that this is just as meaningful as adding up our telephone numbers and calculating our average telephone number.
The whole thing is not yet finished, but one of the encryptions is quite interesting.
Cipher:
a;XQxkd:un3IyG+Ab 0oL=YVXmPewEr8fq9 gtJasFxI=U:Xlh7E1 3RNyAb+lcL2DewCQ0 u5qjz8=Xn=spPGh;; fBciNgZbeaKMLXwFx IvU:YV=m3b8JSsy74 +tEN;uCe0RoP;r1Ld YYfDnYGX;5AgqwUTl 2a7xQ3ViRTb=YTXIZ Yt=mye8Jvs+A90nEN ;lXGjdqTl=VjX7lph bFL2PYptDzfYn=mge wJS8aR4xGEiYY3ZVK XtlcsFl2CbpNFyY2n dM+YG=m0eLJrwPA9f VE5oD1zXbhi8gHcKZ ebaMoxkBC1Y:dT3HY ytI=n;+kQ50lPBeXY hfH=GkczsVC4vNgBL
Solution:
EMOVEDALLREFERENC ESTOPROJECTGUTENB ERGETHEFOLLOWINGS ENTENCEWITHACTIVE LINKSTOOROTHERIMM EDIATEACCESSTOTHE FULLPROJECTGUTENB ERGTMLICENSEMUSTA PPEARPROMINENTLYW HENEVERANYCOPYOFA PROJECTGUTENBERGT MWORKANYWORKONWHI CHTHEPHRASEPROJEC TGUTENBERGAPPEARS ORWITHWHICHTHEPHR ASEPROJECTGUTENBE RGISASSOCIATEDISA CCESSEDDISPLAYEDP ERFORMEDVIEWEDCOP IEDORDISTRIBUTEDT
Key:
dDiZ94bekBHax3y+0PfgIEJF2phcC5mj:uU;Aq7RX=YOnGVto1zKMLw8sNrvSQl-TW AAAABBCCDDDEEEEEEEEEFGGHHHIIIIJKLLLMNNNNOOPQRRRRSSSSSTTTTTUUUVWXYZ
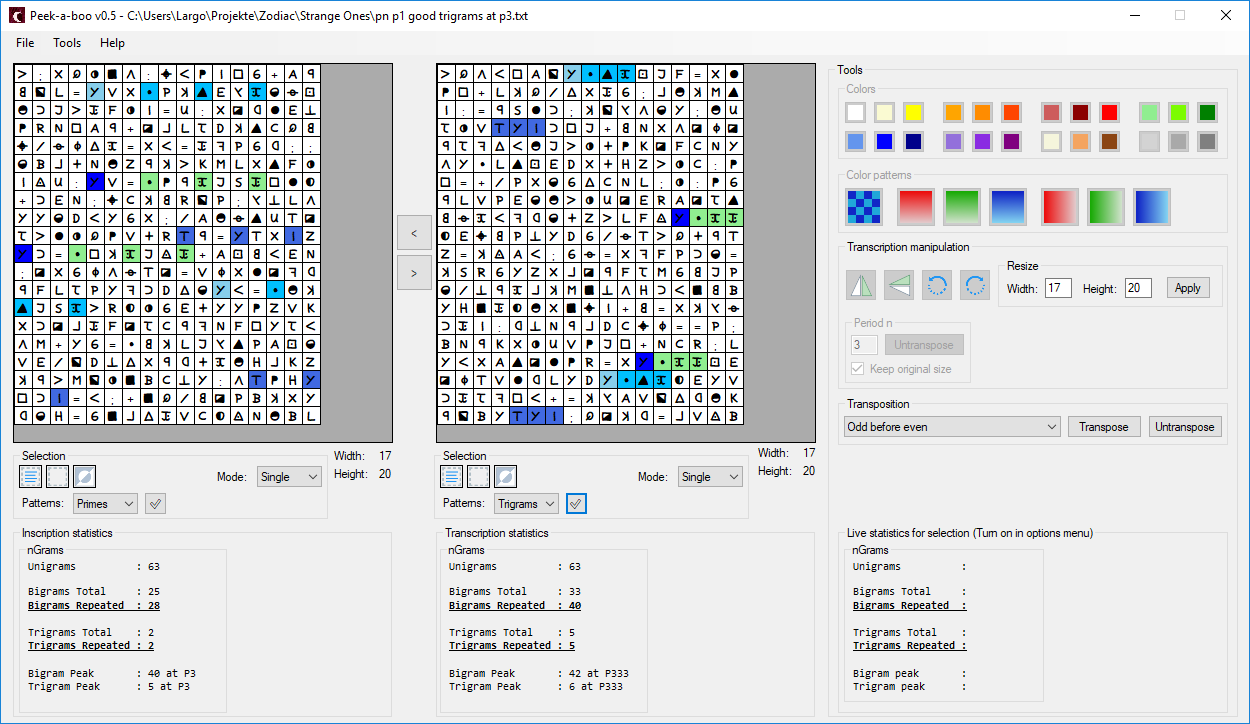
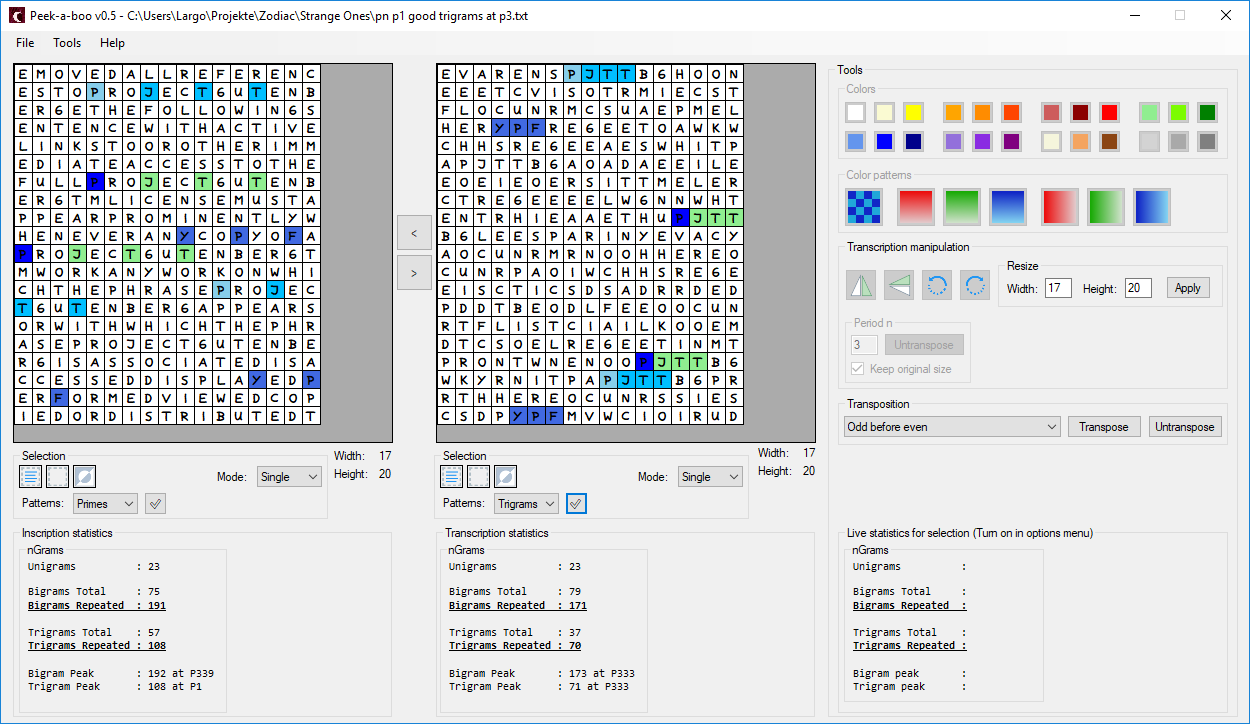
AZDecrypt solves this encryption without any problems. But let us assume that this is not the case and that we would investigate it further. First of all, we would discover a very clear bi- and trigram peak at P3. This is statistically not quite as impressive as P15/P19 at z340, but nevertheless remarkable. One could therefore conclude that there is a transposition. This is obviously not the case. If you decipher the example, it quickly becomes clear where the peak at P3 comes from: There are many repetitive text passages. The following pictures should show what is meant:
The upper picture shows the encrypted variant, the lower picture shows the decrypted one. The original is on the left, P3 untransposed on the right.
I am almost certain that it has already been discussed that P15/P19 does not necessarily have to indicate transposition. Repeated passages of text are also a possible explanation. What do you think of that?
Finally, I have a little challenge. Can someone solve the following cipher? No fancy manipulations, just an easy one. I noticed something during my statistical examinations that gave me an idea. Probably you will succeed very quickly. If not, I maybe have discovered something interesting ![]()
+7vg=rqmyPNHjmasi VZcG;efbnY4Qy3xSI cmPb+j45k:mjC8Rtw H5eigjFJn9KKmCHEj KCjnIt8mclzVZkf+G -B+m;GP52jWmEi049 gjFcVsyhmLjfTXpJ0 9I5ZmB8CvbqWryxaN ;e:opOm+Szni2jLEt h37mj:FVZKmJ1Gcjk nRlIWtgmCWjfQ4PL0 jc+Tzed=J5bi-9Exa uI2UYg5NzsLuL3CmF Eojq:OpmzXv+WjryL 5jDC4KmxajWcmkJG7 mQgYtKXj=1m3FVSRd xul9IKjZP+n8mjaUW i1b-JoGKqjEOm3fjm r::NF=s98VTZLyHjm SUCKj8gnYfct7vzmP
I am almost certain that it has already been discussed that P15/P19 does not necessarily have to indicate transposition. Repeated passages of text are also a possible explanation. What do you think of that?
I am interested to know whether if you slide a large corpus of plain text through homophonic keys of varying efficiency ( from high diffusion of high frequency plain text to low diffusion of high frequency plain text with the symbols spread out more evenly on the key ), whether any will have a spike like P15/19. And then maybe a large corpus of poetry with a lot of rhyming words. I don’t know if it is transposition or not, but take into consideration the count of bigram repeats at P1. It is low while P15/19 is high.
Here is smokie18e, which diffuses the plaint text in period 1 repeats more and in period 19 less. I had to use trial and error and keep fiddling around with the key to do it
2 29 30 52 23 12 54 45 2 6 13 50 43 15 3 16 16
24 37 25 55 63 61 26 52 22 40 46 7 41 36 51 8 27
42 56 52 38 14 50 51 43 15 53 22 23 4 12 39 62 57
55 16 54 14 1 54 61 13 6 2 37 11 24 52 6 40 59
23 45 3 37 11 52 21 23 63 1 48 12 60 14 49 63 17
14 62 2 23 23 50 58 8 23 3 51 53 41 15 1 59 42
56 14 54 14 25 52 10 3 55 12 52 14 13 43 38 32 63
6 39 33 44 55 14 53 23 44 3 55 3 29 30 12 30 53
40 55 21 13 16 3 5 29 14 26 50 17 41 56 36 9 27
37 52 22 23 24 7 12 55 3 38 9 25 8 51 1 19 2
42 17 19 45 13 53 54 25 46 61 23 41 27 52 3 28 24
36 11 39 16 37 40 47 55 14 14 48 38 21 23 49 8 56
31 12 50 52 22 27 51 23 13 23 41 44 14 14 17 39 14
34 52 33 2 36 63 20 45 23 2 53 16 13 3 54 50 4
56 55 52 14 13 46 14 1 47 23 53 21 45 12 13 61 22
26 7 23 5 14 30 43 37 18 54 43 54 22 23 51 57 44
12 49 37 2 52 58 55 3 31 27 36 43 37 23 41 16 53
21 13 52 12 22 12 61 14 14 50 54 32 14 52 62 24 55
23 1 15 24 23 37 9 6 2 55 29 12 10 19 30 3 33
1 37 11 28 26 30 32 52 14 27 34 2 37 11 52 21 42
I really like the pictures.
AZDecrypt solves this encryption without any problems. But let us assume that this is not the case and that we would investigate it further. First of all, we would discover a very clear bi- and trigram peak at P3. This is statistically not quite as impressive as P15/P19 at z340, but nevertheless remarkable. One could therefore conclude that there is a transposition. This is obviously not the case.
I understand your concern and agree that it is a possibility. However, it is vital that you match the ioc of the 340 if you want to do meaningful comparisons. Your cipher has a raw ioc of 1857 while the 340 has 2237. A higher ioc means more bigrams and lessens the chance of outliers.
Finally, I have a little challenge. Can someone solve the following cipher? No fancy manipulations, just an easy one.
Excerpt from the book Dracula by Bram Stoker.
Here is smokie18e, which diffuses the plaint text in period 1 repeats more and in period 19 less. I had to use trial and error and keep fiddling around with the key to do it
It has a raw ioc of 2607, that means it is much harder to transform the bigrams from one period into another. Using the same ioc as the 340 would make it easier, but probably still somewhat difficult.