Sometimes it takes me a while to grasp a certain concept. You are saying that if you look at each row, then there are only 18 symbols repeated in the entire message, but if you shuffle the message that is not going to happen. I do not understand about the frequencies of unique sequence lengths peak at 17 with 26 repeats. And you are saying that if Zodiac encoded before transposing, then the same symbols would more frequently appear in the same rows as compared to the 340. I do understand that, and would like to test it.
Yes, most transposition schemes greatly increase unigram repeats per row (or window) when applied after encoding. doranchak’s explanation is spot on.
With perfect cycles, there are zero unigram repeats when checking by row.
Yes, perfect cycling does decrease the unigram repeats allot. But we find no extensive cycling in the 340. So "do not repeat characters in a certain window, no intentional cycling" becomes the most likely thing because it is also in line with the high peak in the unique sequence lengths and there’s no indication of polyalphabetism. It would not be entirely fair to compare your cipher to the 340 in lights of unigram repeats since it has less repeat potential than the 340.
Why is the problem for me. If he did this intentionally, then what was he thinking? I do not see how this would make a homophonic substitution cryptogram more difficult to solve. Unless of course he was trying to avoid creating period 1 bigram repeats. But then we have the period 15 / 19 repeats. So I wonder if this is created by the cipher unintentionally instead of intentionally.
I think it is easier to apply the encoding this way, since you only need to check your window for repeats. It does indeed not increase the difficulty though figuring out cycles becomes a problem.
I have always preferred transposition before encoding, but have never been able to reconcile the strange cycle score left right top bottom.
The "do not repeat characters in a certain window, no intentional cycling" actually does create cycling very similar to what we see in the 340. Because there is still cycling going on in order not to repeat characters (but not intentional).
I believe Jarlve discovered that Z340 has a peak of 26 occurrences of non-repeating segments of length 17, which is a statistically significant anomaly when compared to randomizations. And especially interesting since the row lengths happen to be 17.
Did I get this right?
Yes, thank you.
Here’s my plot. The red graph is the normal 340. The green graph is the mirrored 340. If his window was equal to the width of the rows (17) then I wonder why the peak would diminish in such a manner after mirroring the cipher. Checking unigram repeats for various row lengths does indicate a window of about 17.
AZdecrypt combine statistics for: 340.txt -------------------------------------------------- Dimension(1,340): 0 Dimension(2,170): 2 Dimension(3,114): 3 Dimension(4,85): 4 Dimension(5,68): 3 Dimension(6,57): 6 Dimension(7,49): 6 Dimension(8,43): 7 Dimension(9,38): 9 Dimension(10,34): 7 Dimension(11,31): 14 Dimension(12,29): 11 Dimension(13,27): 14 Dimension(14,25): 17 Dimension(15,23): 16 Dimension(16,22): 17 Dimension(17,20): 18 Dimension(18,19): 24 Dimension(19,18): 24 Dimension(20,17): 25 Dimension(21,17): 29 Dimension(22,16): 30 Dimension(23,15): 35 Dimension(24,15): 33 Dimension(25,14): 44 Dimension(26,14): 40 Dimension(27,13): 40 Dimension(28,13): 42 Dimension(29,12): 45 Dimension(30,12): 45 Dimension(31,11): 46 Dimension(32,11): 48 Dimension(33,11): 55 Dimension(34,10): 56

And to reiterate. The 340 has a lower flatness than the 408. So if you consider a hypothesis such as cycle randomization due to transposition, you have yet to explain the lower flatness of the symbol frequencies. An inefficient key could do the trick, and is possibly a partial explanation (the "+" symbol, a possible 1:1 substitute) but increased randomization in the symbol selection process does seem the more likely element to me. And that falls into its place with "no intentional cycling".
O.k., I think I am starting to grasp to no repeat window idea. I tend to think that these stats are directly correlated with cycle scores.
Let’s say we have a key, and for letter E these are the symbols: 1 2 3 4 5.
Have you considered that maybe he cycled like this for 9 occurrences for the letter E: 1 2 3 4 5 4 3 2 1 ?
Letter E should appear about 12% of the time, or about 1 of 8 letters + / -. So with this scheme, the two 4s would maybe cause the 26 occurrences of unique symbol strings 17 positions long?
Thanks doranchak and Jarlve for explaining.
I am wondering exactly what symbols are involved, and where these occurrences are.
Hey smokie,
I like your conversion chart, well done there.
Have you considered that maybe he cycled like this for 9 occurrences for the letter E: 1 2 3 4 5 4 3 2 1 ?
No, and that is what moonrock refers to as a palindromic cycle (moonrock did an excellent job at defining different cycle systems) viewtopic.php?f=81&t=3179 So, take a cycle system and come up with a test I guess. I’m kinda skeptic at the moment, I really wonder if Zodiac would have dabbled with such.
1. The perfect cycle, which has substitutions arranged in an unchanging pattern throughout the entire cipher: 12345 – 12345 – 12345 – 12345.
2. The increasingly random cycle, which has substitutions start off in an organized cycle and gradually become random: 12345 – 12345 – 12435 – 24153.
3. The decreasingly random cycle, which is the opposite of the increasingly random cycle: 24153 – 12435 – 12345 – 12345.
4. The random cycle, which has the substitutions arranged in random order: 32415 – 12543 – 41352 – 53124.
5. The concurrent cycle, which has two separate cycles existing at the same time for a single substitution; 1 and 5 cycling, and 2, 3, and 4 cycling in the following example: 12345 – 21354 – 23154 – 23415.
6. The palindromic cycle, which has the substitutions arranged in an order that reads the same forward and backward: 11211 – 11211 – 11211, 12321 – 12321 – 12321, and 123454321.
7. The inverted cycle, which has a uniform cycle inverted to be the opposite of what it was beyond a certain point: 12345 – 12345 – 54321 – 54321, and 11211 – 11211 – 22122 – 22122. The former example is an example of a perfect cycle being inverted, which creates a palindrome, and the latter example is of a palindromic cycle being inverted.
8. The shortened cycle, which has a cycle decrease in length as the ciphertext progresses: 12345 – 12345 – 1234 – 1234 – 123 – 123.
9. The lengthened cycle, which is the opposite of the shortened cycle: 123 – 123 – 1234 – 1234 – 12345 – 12345.
10. The regional cycle, which restricts substitutions to or from specific regions, or areas, of the ciphertext; this restriction typically manifests as either a restriction to specific rows or to specific columns, and, if used exclusively, is the equivalent of a series of simple substitutions.
11. The semi-regional cycle, which has the frequency of substitutions fluctuate between different regions, or areas, of the ciphertext in a similar way to regional cycling. When regional and semi-regional cycles are combined, it increases their level of security. Both regional and semi-regional cycles are capable of being accompanied by non-regional assignment of substitutions.
12. The sequential cycle, which is when one type of cycle is followed by another type of cycle: 12345 – 12345 – 123454321 – 1234321 – 12321; in this example, a perfect cycle changes to a palindromic cycle, which is then shortened.
I am wondering exactly what symbols are involved, and where these occurrences are.
Scroll down in the code box, everything you asked for is there. The positional occurance is displayed in brackets.
Unique sequence frequencies: -------------------------------------------------- Length 1: 5 Length 2: 6 Length 3: 8 Length 4: 9 Length 5: 11 Length 6: 11 Length 7: 14 Length 8: 15 Length 9: 15 Length 10: 18 Length 11: 19 Length 12: 20 Length 13: 20 Length 14: 21 Length 15: 22 Length 16: 23 Length 17: 26 Length 18: 20 Length 19: 15 Length 20: 9 Length 21: 9 Length 22: 8 Length 23: 5 Length 24: 3 Length 25: 3 Length 26: 2 Length 27: 1 Length 28: 1 Length 29: 1 Unique sequences by length and appearance -------------------------------------------------- 1: p (53) 1: + (64) 1: + (237) 1: + (290) 1: + (340) 2: Sp (52) 2: O+ (63) 2: +b (140) 2: t+ (236) 2: L+ (289) 2: ;+ (339) 3: JSp (51) 3: pO+ (62) 3: M+b (139) 3: +^J (159) 3: 4t+ (235) 3: )L+ (288) 3: WCz (293) 3: K;+ (338) 4: HJSp (50) 4: 3pO+ (61) 4: <M+b (138) 4: V+^J (158) 4: V4t+ (234) 4: |)L+ (287) 4: )WCz (292) 4: B_YO (315) 4: |K;+ (337) 5: zHJSp (49) 5: V3pO+ (60) 5: +_NYz (128) 5: d<M+b (137) 5: UV+^J (157) 5: 4b.cV (230) 5: cV4t+ (233) 5: B|)L+ (286) 5: +)WCz (291) 5: tB_YO (314) 5: A|K;+ (336) 6: #zHJSp (48) 6: *V3pO+ (59) 6: O+_NYz (127) 6: 9d<M+b (136) 6: lUV+^J (156) 6: 24b.cV (229) 6: .cV4t+ (232) 6: +L16C< (276) 6: WB|)L+ (285) 6: 7tB_YO (313) 6: 8A|K;+ (335) 7: L#zHJSp (47) 7: 8*V3pO+ (58) 7: +RK2_9M (65) 7: GV.zL|( (114) 7: #O+_NYz (126) 7: +@L9d<M (133) 7: L9d<M+b (135) 7: zlUV+^J (155) 7: 524b.cV (228) 7: b.cV4t+ (231) 7: T+L16C< (275) 7: lWB|)L+ (284) 7: <7tB_YO (312) 7: O8A|K;+ (334) 8: )L#zHJSp (46) 8: p7^l8*V3 (54) 8: l8*V3pO+ (57) 8: FlO-*dCk (90) 8: XGV.zL|( (113) 8: j#O+_NYz (125) 8: z+@L9d<M (132) 8: @L9d<M+b (134) 8: -zlUV+^J (154) 8: f524b.cV (227) 8: cT+L16C< (274) 8: +FlWB|)L (282) 8: FlWB|)L+ (283) 8: W<7tB_YO (311) 8: ZO8A|K;+ (333) 9: ()L#zHJSp (45) 9: ^l8*V3pO+ (56) 9: +ztjd|5FP (72) 9: ^FlO-*dCk (89) 9: cXGV.zL|( (112) 9: fj#O+_NYz (124) 9: Yz+@L9d<M (131) 9: K-zlUV+^J (153) 9: FBc(;8RlG (215) 9: ^f524b.cV (226) 9: .3zBK(Op^ (258) 9: RcT+L16C< (273) 9: <+FlWB|)L (281) 9: dW<7tB_YO (310) 9: zZO8A|K;+ (332) 10: W()L#zHJSp (44) 10: 7^l8*V3pO+ (55) 10: M+ztjd|5FP (71) 10: R^FlO-*dCk (88) 10: 2D(#5+Kq%; (100) 10: UcXGV.zL|( (111) 10: Jfj#O+_NYz (123) 10: NYz+@L9d<M (130) 10: 4K-zlUV+^J (152) 10: +Op7<FBy-U (162) 10: +&BFz69Sy# (201) 10: 5FBc(;8RlG (214) 10: N^f524b.cV (225) 10: c.3zBK(Op^ (257) 10: 2RcT+L16C< (272) 10: C<+FlWB|)L (280) 10: kdW<7tB_YO (309) 10: SzZO8A|K;+ (331) 11: GW()L#zHJSp (43) 11: 9M+ztjd|5FP (70) 11: FP+&4k/p8R^ (79) 11: 8R^FlO-*dCk (87) 11: >2D(#5+Kq%; (99) 11: 2UcXGV.zL|( (110) 11: 2Jfj#O+_NYz (122) 11: _NYz+@L9d<M (129) 11: 64K-zlUV+^J (151) 11: J+Op7<FBy-U (161) 11: .+&BFz69Sy# (200) 11: Fz69Sy#+N|5 (204) 11: |5FBc(;8RlG (213) 11: FN^f524b.cV (224) 11: |c.3zBK(Op^ (256) 11: G2RcT+L16C< (271) 11: 6C<+FlWB|)L (279) 11: FkdW<7tB_YO (308) 11: kSzZO8A|K;+ (330) 12: )By:cM+UZGW( (34) 12: ZGW()L#zHJSp (42) 12: _9M+ztjd|5FP (69) 12: 5FP+&4k/p8R^ (78) 12: p8R^FlO-*dCk (86) 12: F>2D(#5+Kq%; (98) 12: ;2UcXGV.zL|( (109) 12: G2Jfj#O+_NYz (121) 12: A64K-zlUV+^J (150) 12: ^J+Op7<FBy-U (160) 12: M.+&BFz69Sy# (199) 12: BFz69Sy#+N|5 (203) 12: N|5FBc(;8RlG (212) 12: GFN^f524b.cV (223) 12: +|c.3zBK(Op^ (255) 12: qG2RcT+L16C< (270) 12: L16C<+FlWB|) (277) 12: 16C<+FlWB|)L (278) 12: |FkdW<7tB_YO (307) 12: pkSzZO8A|K;+ (329) 13: f)By:cM+UZGW( (33) 13: UZGW()L#zHJSp (41) 13: 2_9M+ztjd|5FP (68) 13: |5FP+&4k/p8R^ (77) 13: k/p8R^FlO-*dC (84) 13: /p8R^FlO-*dCk (85) 13: kF>2D(#5+Kq%; (97) 13: %;2UcXGV.zL|( (108) 13: (G2Jfj#O+_NYz (120) 13: yA64K-zlUV+^J (149) 13: By-U+R/5tE|DY (168) 13: TMKO2<clRJ|*5 (184) 13: 4M.+&BFz69Sy# (198) 13: &BFz69Sy#+N|5 (202) 13: +N|5FBc(;8RlG (211) 13: lGFN^f524b.cV (222) 13: -+|c.3zBK(Op^ (254) 13: MqG2RcT+L16C< (269) 13: p|FkdW<7tB_YO (306) 13: NpkSzZO8A|K;+ (328) 14: pl^VPk|1LTG2dN (5) 14: B(#O%DWY.<*Kf) (21) 14: Kf)By:cM+UZGW( (32) 14: +UZGW()L#zHJSp (40) 14: K2_9M+ztjd|5FP (67) 14: d|5FP+&4k/p8R^ (76) 14: 4k/p8R^FlO-*dC (83) 14: CkF>2D(#5+Kq%; (96) 14: q%;2UcXGV.zL|( (107) 14: |(G2Jfj#O+_NYz (119) 14: cyA64K-zlUV+^J (148) 14: FBy-U+R/5tE|DY (167) 14: bTMKO2<clRJ|*5 (183) 14: MKO2<clRJ|*5T4 (185) 14: T4M.+&BFz69Sy# (197) 14: #+N|5FBc(;8RlG (210) 14: RlGFN^f524b.cV (221) 14: 5-+|c.3zBK(Op^ (253) 14: fMqG2RcT+L16C< (268) 14: )p|FkdW<7tB_YO (305) 14: HNpkSzZO8A|K;+ (327) 15: >pl^VPk|1LTG2dN (4) 15: +B(#O%DWY.<*Kf) (20) 15: *Kf)By:cM+UZGW( (31) 15: M+UZGW()L#zHJSp (39) 15: RK2_9M+ztjd|5FP (66) 15: jd|5FP+&4k/p8R^ (75) 15: &4k/p8R^FlO-*dC (82) 15: dCkF>2D(#5+Kq%; (95) 15: Kq%;2UcXGV.zL|( (106) 15: zL|(G2Jfj#O+_NY (117) 15: L|(G2Jfj#O+_NYz (118) 15: BcyA64K-zlUV+^J (147) 15: <FBy-U+R/5tE|DY (166) 15: pbTMKO2<clRJ|*5 (182) 15: 5T4M.+&BFz69Sy# (196) 15: y#+N|5FBc(;8RlG (209) 15: 8RlGFN^f524b.cV (220) 15: Z5-+|c.3zBK(Op^ (252) 15: .fMqG2RcT+L16C< (267) 15: WcPOSHT/()p|Fkd (296) 15: ()p|FkdW<7tB_YO (304) 15: DHNpkSzZO8A|K;+ (326) 16: R>pl^VPk|1LTG2dN (3) 16: p+B(#O%DWY.<*Kf) (19) 16: <*Kf)By:cM+UZGW( (30) 16: cM+UZGW()L#zHJSp (38) 16: tjd|5FP+&4k/p8R^ (74) 16: +&4k/p8R^FlO-*dC (81) 16: *dCkF>2D(#5+Kq%; (94) 16: +Kq%;2UcXGV.zL|( (105) 16: .zL|(G2Jfj#O+_NY (116) 16: FBcyA64K-zlUV+^J (146) 16: 7<FBy-U+R/5tE|DY (165) 16: |DYBpbTMKO2<clRJ (178) 16: BpbTMKO2<clRJ|*5 (181) 16: *5T4M.+&BFz69Sy# (195) 16: Sy#+N|5FBc(;8RlG (208) 16: c(;8RlGFN^f524b. (217) 16: ;8RlGFN^f524b.cV (219) 16: UZ5-+|c.3zBK(Op^ (251) 16: ^.fMqG2RcT+L16C< (266) 16: zWcPOSHT/()p|Fkd (295) 16: /()p|FkdW<7tB_YO (303) 16: OB*-Cc>MDHNpkSzZ (318) 16: MDHNpkSzZO8A|K;+ (325) 17: ER>pl^VPk|1LTG2dN (2) 17: Np+B(#O%DWY.<*Kf) (18) 17: WY.<*Kf)By:cM+UZG (27) 17: .<*Kf)By:cM+UZGW( (29) 17: :cM+UZGW()L#zHJSp (37) 17: ztjd|5FP+&4k/p8R^ (73) 17: P+&4k/p8R^FlO-*dC (80) 17: -*dCkF>2D(#5+Kq%; (93) 17: 5+Kq%;2UcXGV.zL|( (104) 17: V.zL|(G2Jfj#O+_NY (115) 17: +ZR2FBcyA64K-zlUV (142) 17: 2FBcyA64K-zlUV+^J (145) 17: p7<FBy-U+R/5tE|DY (164) 17: E|DYBpbTMKO2<clRJ (177) 17: YBpbTMKO2<clRJ|*5 (180) 17: |*5T4M.+&BFz69Sy# (194) 17: 9Sy#+N|5FBc(;8RlG (207) 17: Bc(;8RlGFN^f524b. (216) 17: (;8RlGFN^f524b.cV (218) 17: +yBX1*:49CE>VUZ5- (238) 17: VUZ5-+|c.3zBK(Op^ (250) 17: p^.fMqG2RcT+L16C< (265) 17: CzWcPOSHT/()p|Fkd (294) 17: T/()p|FkdW<7tB_YO (302) 17: YOB*-Cc>MDHNpkSzZ (317) 17: >MDHNpkSzZO8A|K;+ (324) 18: HER>pl^VPk|1LTG2dN (1) 18: dNp+B(#O%DWY.<*Kf) (17) 18: DWY.<*Kf)By:cM+UZG (26) 18: Y.<*Kf)By:cM+UZGW( (28) 18: y:cM+UZGW()L#zHJSp (36) 18: O-*dCkF>2D(#5+Kq%; (92) 18: (#5+Kq%;2UcXGV.zL| (102) 18: #5+Kq%;2UcXGV.zL|( (103) 18: b+ZR2FBcyA64K-zlUV (141) 18: R2FBcyA64K-zlUV+^J (144) 18: Op7<FBy-U+R/5tE|DY (163) 18: tE|DYBpbTMKO2<clRJ (176) 18: DYBpbTMKO2<clRJ|*5 (179) 18: J|*5T4M.+&BFz69Sy# (193) 18: 69Sy#+N|5FBc(;8RlG (206) 18: >VUZ5-+|c.3zBK(Op^ (249) 18: Op^.fMqG2RcT+L16C< (264) 18: HT/()p|FkdW<7tB_YO (301) 18: _YOB*-Cc>MDHNpkSzZ (316) 18: c>MDHNpkSzZO8A|K;+ (323) 19: 2dNp+B(#O%DWY.<*Kf) (16) 19: %DWY.<*Kf)By:cM+UZG (25) 19: By:cM+UZGW()L#zHJSp (35) 19: lO-*dCkF>2D(#5+Kq%; (91) 19: D(#5+Kq%;2UcXGV.zL| (101) 19: ZR2FBcyA64K-zlUV+^J (143) 19: R/5tE|DYBpbTMKO2<cl (173) 19: 5tE|DYBpbTMKO2<clRJ (175) 19: RJ|*5T4M.+&BFz69Sy# (192) 19: z69Sy#+N|5FBc(;8RlG (205) 19: E>VUZ5-+|c.3zBK(Op^ (248) 19: (Op^.fMqG2RcT+L16C< (263) 19: OSHT/()p|FkdW<7tB_Y (299) 19: SHT/()p|FkdW<7tB_YO (300) 19: Cc>MDHNpkSzZO8A|K;+ (322) 20: G2dNp+B(#O%DWY.<*Kf) (15) 20: O%DWY.<*Kf)By:cM+UZG (24) 20: +R/5tE|DYBpbTMKO2<cl (172) 20: /5tE|DYBpbTMKO2<clRJ (174) 20: lRJ|*5T4M.+&BFz69Sy# (191) 20: CE>VUZ5-+|c.3zBK(Op^ (247) 20: K(Op^.fMqG2RcT+L16C< (262) 20: POSHT/()p|FkdW<7tB_Y (298) 20: -Cc>MDHNpkSzZO8A|K;+ (321) 21: TG2dNp+B(#O%DWY.<*Kf) (14) 21: #O%DWY.<*Kf)By:cM+UZG (23) 21: U+R/5tE|DYBpbTMKO2<cl (171) 21: clRJ|*5T4M.+&BFz69Sy# (190) 21: BX1*:49CE>VUZ5-+|c.3z (240) 21: 9CE>VUZ5-+|c.3zBK(Op^ (246) 21: BK(Op^.fMqG2RcT+L16C< (261) 21: cPOSHT/()p|FkdW<7tB_Y (297) 21: *-Cc>MDHNpkSzZO8A|K;+ (320) 22: LTG2dNp+B(#O%DWY.<*Kf) (13) 22: (#O%DWY.<*Kf)By:cM+UZG (22) 22: -U+R/5tE|DYBpbTMKO2<cl (170) 22: <clRJ|*5T4M.+&BFz69Sy# (189) 22: yBX1*:49CE>VUZ5-+|c.3z (239) 22: 49CE>VUZ5-+|c.3zBK(Op^ (245) 22: zBK(Op^.fMqG2RcT+L16C< (260) 22: B*-Cc>MDHNpkSzZO8A|K;+ (319) 23: 1LTG2dNp+B(#O%DWY.<*Kf) (12) 23: y-U+R/5tE|DYBpbTMKO2<cl (169) 23: 2<clRJ|*5T4M.+&BFz69Sy# (188) 23: :49CE>VUZ5-+|c.3zBK(Op^ (244) 23: 3zBK(Op^.fMqG2RcT+L16C< (259) 24: |1LTG2dNp+B(#O%DWY.<*Kf) (11) 24: O2<clRJ|*5T4M.+&BFz69Sy# (187) 24: *:49CE>VUZ5-+|c.3zBK(Op^ (243) 25: k|1LTG2dNp+B(#O%DWY.<*Kf) (10) 25: KO2<clRJ|*5T4M.+&BFz69Sy# (186) 25: 1*:49CE>VUZ5-+|c.3zBK(Op^ (242) 26: Pk|1LTG2dNp+B(#O%DWY.<*Kf) (9) 26: X1*:49CE>VUZ5-+|c.3zBK(Op^ (241) 27: VPk|1LTG2dNp+B(#O%DWY.<*Kf) (8) 28: ^VPk|1LTG2dNp+B(#O%DWY.<*Kf) (7) 29: l^VPk|1LTG2dNp+B(#O%DWY.<*Kf) (6) Unique sequence frequency mapping -------------------------------------------------- 18 17 16 15 14 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 22 21 20 19 18 17 18 17 16 15 14 13 12 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 8 10 9 8 7 6 5 4 3 2 1 7 15 14 13 12 11 10 9 17 16 15 14 13 12 11 17 16 15 14 13 13 12 11 10 9 8 19 18 17 16 15 14 13 12 11 10 19 18 18 17 16 15 14 13 12 11 10 9 8 7 17 16 15 15 14 13 12 11 10 9 8 7 6 5 11 10 9 8 7 8 7 6 5 4 3 2 18 17 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 12 11 10 18 17 16 15 14 13 23 22 21 20 19 20 19 18 17 16 18 17 16 15 14 13 14 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 13 12 11 19 18 17 16 15 14 13 12 11 10 9 17 16 17 16 15 14 13 12 11 10 9 8 7 6 5 7 6 5 4 3 2 1 17 22 21 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 12 12 11 10 9 8 8 7 6 5 4 3 2 1 5 4 3 17 16 15 21 20 19 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 18 17 16 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1
Mapping to color, brighter is a longer unique sequence length. A strong reboot can be noticed around row 10 and 11, it shows as a square.

moonrock did an excellent job at defining different cycle systems
Yes I agree. I am adding a link to his classification system to my first post. I really like the effort that he put into it and am going to have to use words like "palindromic" whenever possible.
Thanks for the info. I will ponder it. And maybe at some point re-tool my encoder spreadsheet so that I can encode with some of moonrock’s cycle types. See what happens.
I believe Jarlve discovered that Z340 has a peak of 26 occurrences of non-repeating segments of length 17, which is a statistically significant anomaly when compared to randomizations. And especially interesting since the row lengths happen to be 17.
Did I get this right?Yes, thank you.
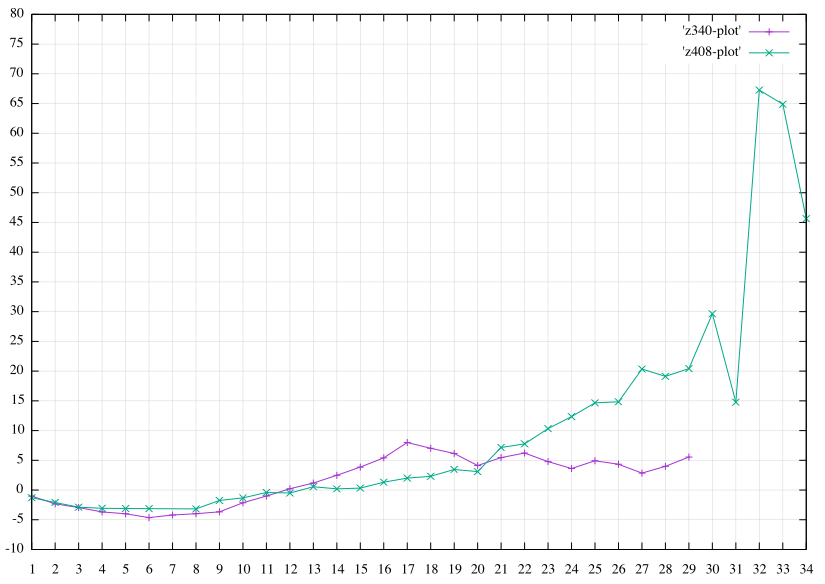
I was curious about the statistical significance of your observation when compared to randomizations, especially when compared to z408. I found that z408’s longer non-repeating segments are much more statistically significant than z340’s non-repeating segments. Thus the effect in z340 is muted a bit when compared to z408. Nevertheless, the peak at length 17 in z340 has the highest significance for z340 when compared to all other segment lengths. Consider this plot of both z340 and z408 together:
The x-axis is the non-repeating segment length. The y-axis is the "sigma" value which indicates statistical significance. First, I found mean and standard deviation of non-repeating segments for 100,000 randomizations of the ciphers. Then sigma is computed as the number of standard deviations the actual z340’s or z408’s observation is seen to be from the mean of the randomizations.
I don’t know what to conclude from this. The peak at length 17 for z340 is still very interesting. But the significance is muted compared to z408’s longer non-repeating segments. Much like the cycles in z340 are muted compared to z408, and z340’s bigrams are muted compared to z408’s.
Hey doranchak,
I think you must have an error somewhere. Your test shows sigma 7.5 for segment length 17 with 26 repeats in the 340. And sigma 45 for segment length 34 with 1 repeat in the 408. I ran a couple of tests and even within only 100.000 randomizations a segment with a length of 39 and 1 repeat was returned for the 408 which should then at least equal a sigma of 45. Also, easily a segment length of 32 with 3 repeats just as in the 408 (sigma 67.5) was recovered from 1.000.000 randomizations of the 408. In 10.000.000 randomizations nothing matched the 340’s peak at segment length 17 with 26 repeats.
Following my hypothesis "do not repeat characters in a certain window, no intentional cycling" the 340 should have a higher sigma than the 408 on your test because it was then the author’s goal not to repeat characters per.
Hey doranchak,
I think you must have an error somewhere. Your test shows sigma 7.5 for segment length 17 with 26 repeats in the 340. And sigma 45 for segment length 34 with 1 repeat in the 408. I ran a couple of tests and even within only 100.000 randomizations a segment with a length of 39 and 1 repeat was returned for the 408 which should then at least equal a sigma of 45.
Z408 does not have a non-repeat segment of length 39 so I did not include looking for it in the randomizations. The longest was 34.
The reason sigma is 45 for segment length 34 in z408 is because for the 100,000 randomizations, the mean repeats for segment length 45 was very close to zero, and the standard deviation is also very small. Actual z408’s number of repeats for length 34 is 1 which is a big number when compared to the small standard deviation of the randomizations. But the number of repeats for length 39 in the actual z408 is zero, which is very close to the mean, so it is a small fraction of standard deviations away from the randomizations’ mean. In other words, the actual z408 meets expectations for length 39 but greatly exceeds them for length 34. I hope I thought that through correctly. Does it make sense?
Also, easily a segment length of 32 with 3 repeats just as in the 408 (sigma 67.5) was recovered from 1.000.000 randomizations of the 408. In 10.000.000 randomizations nothing matched the 340’s peak at segment length 17 with 26 repeats.
I repeated the test for those lengths to help make this clear. The numbers are slightly different but here is the reasoning:
Among 100,000 shuffles of Z340, the average number of repeats for length 17 was found to be 6.25 with a standard deviation of 2.46. The actual number of repeats in Z340 is observed to be 26. Thus the sigma = (repeats-mean)/stddev = (26-6.25)/2.46 = 8.03.
Among 100,000 shuffles of Z408, the average number of repeats for length 32 was found to be 0.0018 with a standard deviation of 0.045. The actual number of repeats in Z408 is observed to be 3. Thus the sigma = (repeats-mean)/stddev = (3-0.0018)/0.045 = 66.6.
What I could conclude from this is it is much harder to see 3 occurrences of non-repeating substrings of length 32 in randomizations of z408 than it is to see 26 occurrences of non-repeating substrings of length 17 in randomizations of z340. But you are right that a peak of 26 was not observed in any of the randomizations. I’m not sure how to reconcile that with the actual values for mean and standard deviation for these randomizations. I’ll run some more tests to see if I can uncover any mistakes.
Among 100,000 shuffles of Z340, the average number of repeats for length 17 was found to be 6.25 with a standard deviation of 2.46. The actual number of repeats in Z340 is observed to be 26. Thus the sigma = (repeats-mean)/stddev = (26-6.25)/2.46 = 8.03.
Among 100,000 shuffles of Z408, the average number of repeats for length 32 was found to be 0.0018 with a standard deviation of 0.045. The actual number of repeats in Z408 is observed to be 3. Thus the sigma = (repeats-mean)/stddev = (3-0.0018)/0.045 = 66.6.
Okay. I’m not 100% sure but this calculation does seem to expect a linear range of values, where each value (number of repeats) have an equal chance of occuring. So perhaps you need to come up with the sigmas for each repeat value and then base the final calculation of that?
I’m working on a frequency table, hold on.
OK here’s a run of 1,000,000 randomizations:
Z408 (non-repeating segments of length 32):
Min: 0
Max: 3
Mean: 0.00178699999999983
Std dev: 0.044652084215366414
Sigma: 67.14609301413539
Frequencies: {0=998314, 1=1589, 2=93, 3=4}
Z340 (non-repeating segments of length 17):
Min: 0
Max: 24
Mean: 6.2571610000000035
Std dev: 2.4665711633876595
Sigma: 8.00416355021544
Frequencies: {0=1694, 1=11041, 2=35718, 3=76917, 4=123054, 5=154859, 6=162316, 7=144531, 8=112690, 9=77434, 10=47950, 11=26694, 12=13797, 13=6534, 14=2873, 15=1209, 17=157, 16=449, 19=22, 18=55, 21=1, 20=4, 24=1}
Frequencies: {0=998314, 1=1589, 2=93, 3=4}
So based on that, we can say: Three non-repeat segments of length 32 were seen in only 4 of 1,000,000 shuffles. So the mean is (4/1,000,000).
The deviations would then be:
999,996 * (0 – 4/1,000,000)^2 = 0.000015999936
4 * (1 – 4/1,000,000)^2 = 3.999968000064
Variance is then the average of the deviations: (3.999968000064 + 0.000015999936) / 1,000,000 = 0.000003999984
Standard deviation is the square root of the variance: 0.002
So, in actual z408, we have 1 occurrence where non-repeat segment of length of 32 was seen 3 times. Therefore, sigma = (1-4/1,000,000)/0.002 = 500.
We can’t really follow a similar logic with Z340 since a count of 26 is never observed for any of the randomizations. So in this case, the direct comparison seems to show how rare the event truly is. But I can’t figure out why the means and standard deviations of the counts themselves don’t show us this. Maybe you are right and it has to do with assuming the counts are linear or something.
I fully understand the calculations and your reasoning. I think you can only compare sigmas if the distribution curves are similar.
Frequencies: {0=998314, 1=1589, 2=93, 3=4} and Frequencies: {0=1694, 1=11041, 2=35718, 3=76917, 4=123054, 5=154859, 6=162316, 7=144531, 8=112690, 9=77434, 10=47950, 11=26694, 12=13797, 13=6534, 14=2873, 15=1209, 17=157, 16=449, 19=22, 18=55, 21=1, 20=4, 24=1} do not follow similar curves and cannot be directly compared to eachother.
The practical value of understanding the standard deviation of a set of values is in appreciating how much variation there is from the average (mean).
Then it seems unpractical to use the standard deviation as a replacement for actual chance values (without proper normalization of some kind) because it is a tool to measure the distance from the mean given the nature of the curve.
10.000.000 randomizations:
340: ---------------- 17, 1: 110992 17, 2: 360243 17, 3: 771592 17, 4: 1226283 17, 5: 1549050 17, 6: 1620484 17, 7: 1445301 17, 8: 1124017 17, 9: 775980 17, 10: 479126 17, 11: 268887 17, 12: 137745 17, 13: 65463 17, 14: 28714 17, 15: 11791 17, 16: 4566 17, 17: 1665 17, 18: 565 17, 19: 181 17, 20: 61 17, 21: 15 17, 22: 3 17, 23: 3 408: ---------------- 32, 1: 14858 32, 2: 867 32, 3: 56 32, 4: 4
Unique String Length Statistic
I made 400 cryptograms with certain rules to see how they compare to the Zodiac 340 unique string length statistics.
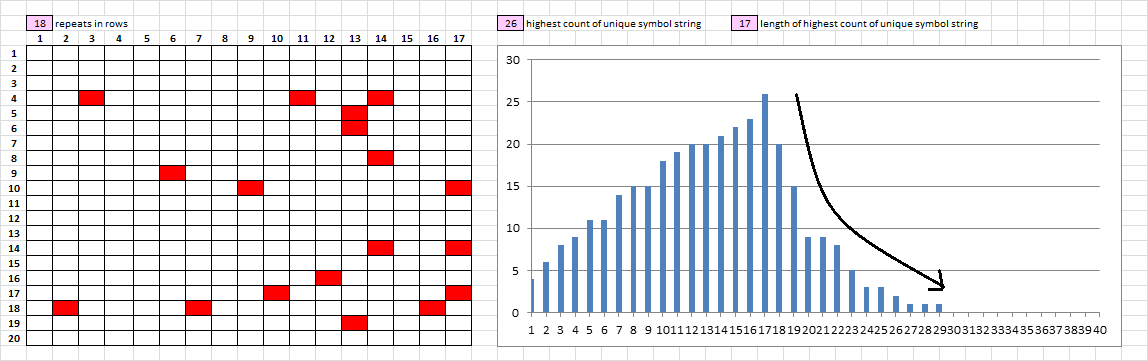
1. Below left are the positions where, going row by row, repeats occur. There are 18 total. Below right x axis is unique string length; y axis is count. It is very interesting how, after the spike at 26 count unique strings of length 17, the counts drop very quickly for longer string lengths. The messages that I made generally had more bell curve shapes.
2. O.k., here are the rules. 1 of each of Jarlve’s 100 plaintext message library with homophonic encoding at 0% random symbol selection ( perfect cycles ), 10% random symbol selection, 20% random symbol selection, and 30% random symbol selection. The 340 cycle scores, as compared to practice homophonic cryptograms, puts the 340 at about 25% to 30% random symbol selection. I mapped one symbol to the three highest count plaintext to simulate the + symbol. It has a count in the mid twenties, and doesn’t appear to cycle well with other symbols. If the plaintext was transposed before encoding, then it would be heavily represented in the period repeats.
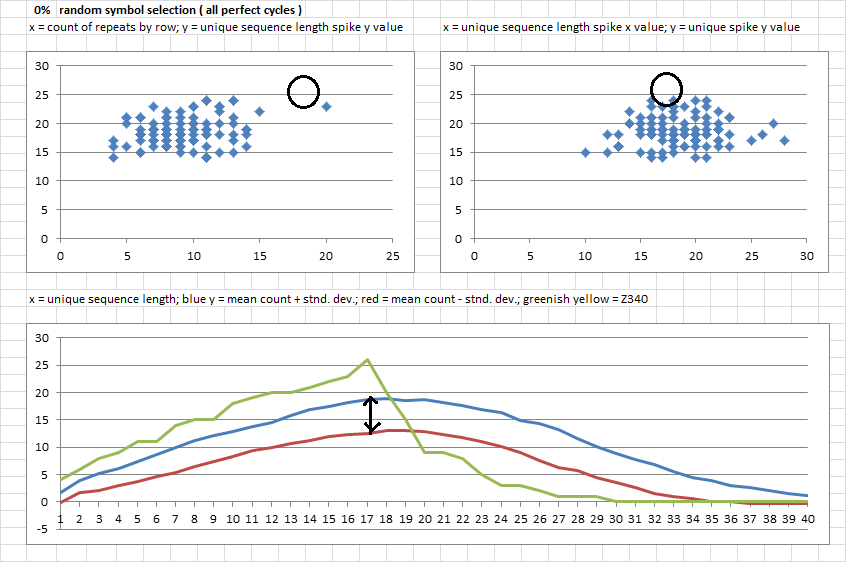
3. Here is how to interpret the charts. With perfect cycles, upper left scatter graph. X axis is the count of repeats by row; Y axis is the spike y value for the unique string lengths. The circle is about where the 340 is. You can see with perfect cycles, all but one of the 100 messages had lower counts of repeats by row. But none had a spike as high as 26 for any unique string length.
Upper right scatter graph. X axis is the unique string length and Y axis is the spike y value. Circle is about where the 340 is. With perfect cycles, it was easy to generate unique stings longer than 17, but none of the string lengths had a count of 26.
Chart below. I calculated the mean value of all of the messages for each unique string length and the standard deviation. The blue line is the mean plus the standard deviation, and the red line is the mean minus the standard deviation. The greenish yellow line is the 340. The black line that I made shows that of the 100 messages, the count of unique strings length 17 was between about 13 and 19. The spike was generally about length 19 but below count of 20.