Also, if you relocated letters (the skips) to the end of the message then you better remove them manually since these act as additional nulls.
What about the n grams? Do you think that 6 grams is better than 5 grams for null skip detection, or maybe lower n grams? I would think higher, but maybe not.
What about the n grams? Do you think that 6 grams is better than 5 grams for null skip detection, or maybe lower n grams? I would think higher, but maybe not.
It is hard to say but I will try it eventually as part of the optimization process. It solved all three of your latest ciphers in about 2 hours so now I feel confident that 10 to 12 nulls/skips should be crackable.
Thinking of adding a heatmap, let the solver run for a while, then after stopping the run AZdecrypt outputs a null and skip heatmap showing the most frequent assigned positions.
How is a "transposition period 20" defined? Are you taking the 1st, then the 21st, then the 41st etc until end to get a first line of 17 symbols, then 2nd, 22nd, 42nd, etc to get a second line of 17 symbols, etc, and then concatenate the 20 lines into one string? That would be like flipping the cipher diagonally, or taking the columns as rows, one after the other.
When applied this way, then smokie treats cipher at Wed Mar 21, 2018 1:49 pm, which was:
28 20 16 31 12 1 13 21 39 14 3 32 3 24 4 8 57 31 1 18 2 25 22 13 45 47 17 12 49 13 43 9 56 29 50 40 47 14 36 6 33 51 15 10 52 34 15 63 33 14 32 14 41 60 15 39 58 6 49 11 39 12 5 8 40 13 50 14 3 6 4 63 48 57 4 26 36 54 12 51 27 2 52 41 23 16 12 55 31 37 58 49 24 56 50 38 32 26 16 42 35 48 61 9 4 16 31 39 26 63 10 34 46 17 40 27 24 62 53 41 36 18 11 3 62 8 25 20 54 38 55 43 42 26 16 56 53 39 60 45 51 40 1 50 17 54 56 13 48 18 21 49 57 54 53 19 61 36 4 12 3 35 54 50 12 23 32 45 62 5 12 33 18 60 23 41 13 14 51 63 4 36 3 61 22 31 15 27 58 55 2 46 3 21 4 12 24 32 60 22 16 8 31 1 24 56 52 30 6 42 7 1 10 3 51 61 38 32 2 1 53 23 39 47 59 48 29 12 5 19 30 27 14 50 54 2 18 55 62 31 15 12 60 11 13 3 25 7 14 15 24 51 56 52 21 55 54 21 55 17 45 61 8 49 46 60 63 35 47 9 56 35 12 22 4 24 13 40 14 41 1 36 2 26 34 27 4 43 42 21 50 53 10 12 37 51 47 6 45 17 38 39 52 59 12 35 49 13 4 24 42 41 19 33 11 7 61 14 15 25 20 39 50 26 1 18 27 12 29 49 34 54 41 17 44 40 21 32 60 36
changes to
28 31 50 14 3 16 61 41 53 54 12 27 24 23 62 55 12 21 49 26 20 1 40 41 6 12 9 36 39 53 33 58 56 39 31 54 22 50 13 1 16 18 47 60 4 55 4 18 60 19 18 55 52 47 15 21 4 53 4 18 31 2 14 15 63 31 16 11 45 61 60 2 30 59 12 55 24 10 24 27 12 25 36 39 48 37 31 3 51 36 23 46 6 48 60 17 13 12 42 12 1 22 6 58 57 58 39 62 40 4 41 3 42 29 11 45 40 37 41 29 13 13 33 6 4 49 26 8 1 12 13 21 7 12 13 61 14 51 19 49 21 45 51 49 26 24 63 25 50 3 14 4 1 5 3 8 41 47 33 34 39 47 15 11 36 56 10 20 17 35 51 12 10 19 25 49 1 6 11 54 14 17 10 39 54 50 34 54 54 54 63 24 3 30 7 46 36 45 7 41 3 12 52 12 12 38 46 38 56 50 4 32 51 27 14 60 2 17 61 17 32 49 34 5 51 32 17 55 13 12 36 60 61 14 15 63 26 38 14 44 3 13 15 8 27 26 40 43 48 23 3 22 38 50 24 35 34 39 15 40 24 43 63 40 2 16 27 42 18 32 61 16 32 54 51 47 27 52 25 21 4 9 33 13 52 42 24 26 21 45 22 8 2 2 56 9 4 59 20 32 8 56 14 50 41 35 62 16 49 62 31 31 1 18 52 56 43 12 39 60 57 29 32 14 23 48 53 56 57 5 15 1 53 55 21 35 42 35 50 36
which conflicts with the solution of
Null(73), Null(110), Null(45), Null(267), Null(177) JAMESWASSHINERING 28 31 50 14 3 16 61 41 53 54 12 27 24 23 62 55 12 DISBODYFELTRAWASI 21 49 26 20 1 40 41 6 12 9 36 39 53 33 58 56 39 etc
on the symbol 41, which in first line is a S on 8th position, and a Y in second line on 7th position.
So that I guess I somehow misunderstood what "P20" stands for.
Can you explain more what the transposition is that you apply? Is there within the blocks of 20 another degree of freedom, eg. instead of going sequentially 1,2,3 … 20 in a different order?
How is a "transposition period 20" defined?
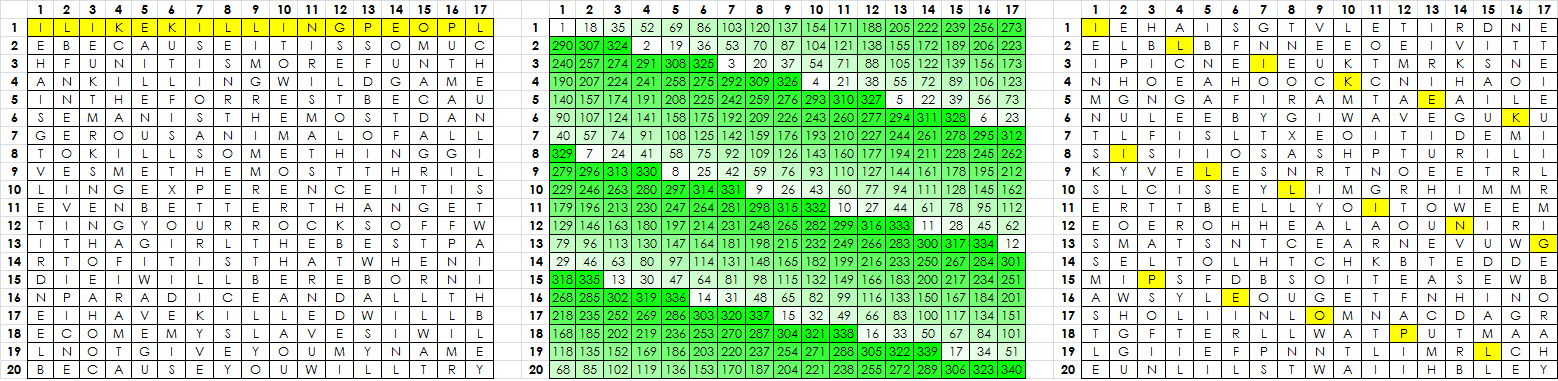
Example of a period 20 transposition applied to a line of numbers from 1 to 340:
1 18 35 52 69 86 103 120 137 154 171 188 205 222 239 256 273 290 307 324 2 19 36 53 70 87 104 121 138 155 172 189 206 223 240 257 274 291 308 325 3 20 37 54 71 88 105 122 139 156 173 190 207 224 241 258 275 292 309 326 4 21 38 55 72 89 106 123 140 157 174 191 208 225 242 259 276 293 310 327 5 22 39 56 73 90 107 124 141 158 175 192 209 226 243 260 277 294 311 328 6 23 40 57 74 91 108 125 142 159 176 193 210 227 244 261 278 295 312 329 7 24 41 58 75 92 109 126 143 160 177 194 211 228 245 262 279 296 313 330 8 25 42 59 76 93 110 127 144 161 178 195 212 229 246 263 280 297 314 331 9 26 43 60 77 94 111 128 145 162 179 196 213 230 247 264 281 298 315 332 10 27 44 61 78 95 112 129 146 163 180 197 214 231 248 265 282 299 316 333 11 28 45 62 79 96 113 130 147 164 181 198 215 232 249 266 283 300 317 334 12 29 46 63 80 97 114 131 148 165 182 199 216 233 250 267 284 301 318 335 13 30 47 64 81 98 115 132 149 166 183 200 217 234 251 268 285 302 319 336 14 31 48 65 82 99 116 133 150 167 184 201 218 235 252 269 286 303 320 337 15 32 49 66 83 100 117 134 151 168 185 202 219 236 253 270 287 304 321 338 16 33 50 67 84 101 118 135 152 169 186 203 220 237 254 271 288 305 322 339 17 34 51 68 85 102 119 136 153 170 187 204 221 238 255 272 289 306 323 340
The nulls are removed before untransposing period 20. The positions of the candidate nulls 45, 73, 110, 177 and 267 are marked as symbol 99:
28 20 16 31 12 1 13 21 39 14 3 32 3 24 4 8 57 31 1 18 2 25 22 13 45 47 17 12 49 13 43 9 56 29 50 40 47 14 36 6 33 51 15 10 99 34 15 63 33 14 32 14 41 60 15 39 58 6 49 11 39 12 5 8 40 13 50 14 3 6 4 63 99 57 4 26 36 54 12 51 27 2 52 41 23 16 12 55 31 37 58 49 24 56 50 38 32 26 16 42 35 48 61 9 4 16 31 39 26 99 10 34 46 17 40 27 24 62 53 41 36 18 11 3 62 8 25 20 54 38 55 43 42 26 16 56 53 39 60 45 51 40 1 50 17 54 56 13 48 18 21 49 57 54 53 19 61 36 4 12 3 35 54 50 12 23 32 45 62 5 12 33 18 60 23 41 99 14 51 63 4 36 3 61 22 31 15 27 58 55 2 46 3 21 4 12 24 32 60 22 16 8 31 1 24 56 52 30 6 42 7 1 10 3 51 61 38 32 2 1 53 23 39 47 59 48 29 12 5 19 30 27 14 50 54 2 18 55 62 31 15 12 60 11 13 3 25 7 14 15 24 51 56 52 21 55 54 21 55 17 45 61 8 49 46 60 99 35 47 9 56 35 12 22 4 24 13 40 14 41 1 36 2 26 34 27 4 43 42 21 50 53 10 12 37 51 47 6 45 17 38 39 52 59 12 35 49 13 4 24 42 41 19 33 11 7 61 14 15 25 20 39 50 26 1 18 27 12 29 49 34 54 41 17 44 40 21 32 60 36
Are then removed going from left-to-right, top-to-bottom:
28 20 16 31 12 1 13 21 39 14 3 32 3 24 4 8 57 31 1 18 2 25 22 13 45 47 17 12 49 13 43 9 56 29 50 40 47 14 36 6 33 51 15 10 34 15 63 33 14 32 14 41 60 15 39 58 6 49 11 39 12 5 8 40 13 50 14 3 6 4 63 57 4 26 36 54 12 51 27 2 52 41 23 16 12 55 31 37 58 49 24 56 50 38 32 26 16 42 35 48 61 9 4 16 31 39 26 10 34 46 17 40 27 24 62 53 41 36 18 11 3 62 8 25 20 54 38 55 43 42 26 16 56 53 39 60 45 51 40 1 50 17 54 56 13 48 18 21 49 57 54 53 19 61 36 4 12 3 35 54 50 12 23 32 45 62 5 12 33 18 60 23 41 14 51 63 4 36 3 61 22 31 15 27 58 55 2 46 3 21 4 12 24 32 60 22 16 8 31 1 24 56 52 30 6 42 7 1 10 3 51 61 38 32 2 1 53 23 39 47 59 48 29 12 5 19 30 27 14 50 54 2 18 55 62 31 15 12 60 11 13 3 25 7 14 15 24 51 56 52 21 55 54 21 55 17 45 61 8 49 46 60 35 47 9 56 35 12 22 4 24 13 40 14 41 1 36 2 26 34 27 4 43 42 21 50 53 10 12 37 51 47 6 45 17 38 39 52 59 12 35 49 13 4 24 42 41 19 33 11 7 61 14 15 25 20 39 50 26 1 18 27 12 29 49 34 54 41 17 44 40 21 32 60 36
Untranspose period 20 gives:
28 2 33 12 52 61 3 50 50 22 24 59 13 46 27 35 18 20 25 51 5 41 9 62 17 12 31 56 48 3 60 4 49 27 16 22 15 8 23 4 8 54 23 15 52 29 25 35 43 13 12 31 13 10 40 16 16 25 56 32 27 30 12 7 47 42 4 29 12 45 34 13 12 31 20 13 45 58 6 5 14 9 21 24 49 1 47 15 50 55 39 54 48 62 55 42 19 15 56 50 42 34 13 17 63 14 31 26 38 18 5 2 7 30 24 35 53 41 54 21 12 33 3 37 10 55 21 12 46 1 27 51 12 10 19 41 39 49 14 6 58 34 43 49 33 3 10 14 56 22 12 33 17 14 13 32 4 49 46 42 57 18 21 3 50 52 4 37 11 44 3 43 14 63 24 17 26 54 60 4 51 54 21 24 51 7 40 32 9 41 57 56 40 16 53 23 12 61 2 55 13 47 61 21 3 56 60 4 50 27 56 19 41 24 38 18 54 40 6 14 32 24 29 15 26 38 24 53 61 14 32 32 55 21 14 45 15 60 4 50 39 36 32 62 39 36 51 60 2 62 55 41 17 25 36 8 40 58 54 26 53 60 4 63 22 1 31 17 1 38 20 57 47 6 12 16 41 45 12 4 16 53 15 45 36 39 39 31 14 49 51 42 36 51 3 36 8 23 12 61 2 52 50 1 36 11 27 35 18 40 35 3 31 39 60 8 26 59 26 18 6 39 2 48 11 1 54 61 1 47 11 49 34 12 1
Which solves into (a better solution is possible, I just took the first one that appeared):
Score: 23907.02 Ioc: 0.06368 Ngrams: 391 PC-cycles: 560 JAMESWASSHINERING DISBODYFELTRAWASI FHEDHADTHESKINPEE LEDOFFITLIKECROAK ERMEELDERUBBEDHIS ARESTOTRYTOGETSOM EFRELINGBACKINTOT HEMANDTHERAISEDGO OSEBUMPSMADETHEMF EELASROUGHASSANDP APERIFITWASTHISCO LDOUTOFTHEWATERWH ATWASITGOINGTOBEL IKEINITWELLTHEREW ASONLYONSWAYTOFIN DOUTITWARHALFANDU RBEFOREAFTERNOOLE SSONSANDHEWASSAND INGONALOWDINIGBOA RDATWARDSMEA
Period transpose/untranspose FreeBASIC code:
for i=1 to period for j=i to cipher_length step period k+=1 if transpose=1 then new_cipher(j)=old_cipher(k) end if if untranspose=1 then new_cipher(k)=old_cipher(j) end if next j next i
How is a "transposition period 20" defined?
Good to see you. Simple ( not keyed ) columnar, or, route transposition. Inscribe a message left right top bottom into a 17 x 20 rectangle, read from the inscription rectangle top bottom left right, and transcribe into a 17 x 20 transcription rectangle left right top bottom. But you could inscribe horizontally from any corner, read vertically from any corner, and transcribe horizontally from any corner and get a message that is just the same as far as the solver is concerned. I make transposition matrices with original symbol position numbers transposed, for a quick way to make transposition messages.
The 340 has a bigram spike at period 19. I use period 20 for some test messages because it is simple, it uses exactly 340 letters. Feel free to ask any questions.
Thank you both. This level of detail is exactly what I need to understand why my own code does not converge on the posted ciphers. I’ll be back!
I am using the program for the 2/2 and have a partial solve. The program definitely works, but I have a small laptop that maybe is not as fast. I am getting phrases, multiple words that all go together in context. I will let it go for a while longer, but there is enough to know that there is a message.
Hill climber iterations: 1642/7400 @ 500000 Score: 23102.31 Ioc: 0.06758 Ngrams: 328 PC-cycles: 3966 Key: Nulls(4,92), Skips(8,246) ALLTHETRAHESOFAFF INITYWITHORCONSCI OUSNESSOFTHEBEOWU EFTHATWECANDISCOV ERANDTHEYAREVERYF UWARESUCHASTOFAVO URTHISDATETHEONLY COMPLETEPARALLELT OTHEFABLEISFOUNDI NTHEICELANDICSAGA OFGRETTIRWHOISAWI NDOFHORTHERNHERCU LESTEISHEROPERFOR MSMANYGREATFEATSB UTTHEREAEETHREEWH ICHBELONRTOTHESUP ERNATURAGINONEOFT HESEHEWRLSTLESWIT HAFIENDCELLEDGLAA NDWILLSAIMANDTH
but I have a small laptop that maybe is not as fast
What CPU do you have? How much MIPS do you get? If it is an i7 try putting CPU threads to 4 or 6.
I am using the program for the 2/2 and have a partial solve. The program definitely works, but I have a small laptop that maybe is not as fast. I am getting phrases, multiple words that all go together in context. I will let it go for a while longer, but there is enough to know that there is a message.
Hill climber iterations: 1642/7400 @ 500000 Score: 23102.31 Ioc: 0.06758 Ngrams: 328 PC-cycles: 3966 Key: Nulls(4,92), Skips(8,246) ALLTHETRAHESOFAFF INITYWITHORCONSCI OUSNESSOFTHEBEOWU EFTHATWECANDISCOV ERANDTHEYAREVERYF UWARESUCHASTOFAVO URTHISDATETHEONLY COMPLETEPARALLELT OTHEFABLEISFOUNDI NTHEICELANDICSAGA OFGRETTIRWHOISAWI NDOFHORTHERNHERCU LESTEISHEROPERFOR MSMANYGREATFEATSB UTTHEREAEETHREEWH ICHBELONRTOTHESUP ERNATURAGINONEOFT HESEHEWRLSTLESWIT HAFIENDCELLEDGLAA NDWILLSAIMANDTH
ALL THE TRAHES OF AFFINITY WITH OR CONSCIOUSNESS OF THE BElie
EF THAT WE CAN DISCOVER AND THEY ARE VERY F aWARE SUCH AS TO FAVO
UR THIS DATE THE ONLY COMPLETE PARALLEL TO THE FABLE IS FOUND I
N THE ICELANDIC SAGA OF GRETTIR WHO I SAW IN DOFHOR wHERe HERCU
LES ThIS HERO PERFORMS MANY GREAT FEATS BUT THERE ArE THREE WH
ICH BELONg TO THE SUPER NATURAl IN ONE OF THESE HE WReSTLES WITH
A FIEND CaLLED GLAAND WILLS AIM AND TH
That is a very slow CPU smokie, I pity you, leave the AZdecrypt CPU thread setting at 1 or 2.
What about the n grams? Do you think that 6 grams is better than 5 grams for null skip detection, or maybe lower n grams? I would think higher, but maybe not.
I did some testing and for AZdecrypt 5-grams are optimal by a wide margin for 340 length 63 symbol ciphers with a period + nulls & skips scheme.
That is a very slow CPU smokie, I pity you.
![]()
I will go to the computer store in a while and at least look at some new computers. I have some other near future expenses on the horizon that I have to plan for.
Anyway, I really do like the new solver. I did get a perfect solution for the 2/2 eventually, and am working on the 4/4 now. So what is the plan now? Start with 1, then 2, then 3, and up and up to 10, 11, 12, skips + nulls. Let the computer run for a really long time on each. And if no solution we know that this isn’t the problem? I think that if that is done we should expand the +, don’t you? Do you want another test message, one with a +, and 11 nulls in the exact same positions as the W and theta symbols?
By the way, I like the darkened triangle for a null also. It does not exist in any P15, P19, P29, P78, pivot, or isomorphic cycle pattern. It was a polyphone in the 408, a special symbol that acted differently than the others. There are four of them in the 340, and one of them is in the signature.
Thanks a lot for the solver.