So what is the plan now? Start with 1, then 2, then 3, and up and up to 10, 11, 12, skips + nulls. Let the computer run for a really long time on each. And if no solution we know that this isn’t the problem? I think that if that is done we should expand the +, don’t you?
I am currently optimizing the period + nulls & skips solver and that may take another couple of weeks.
Yes, up to about 12 nulls/skips for period 15 and 19. Include the reversed directions of each period also? And remove characters (up to how many) at the end of the cipher? How many variations are we then looking at?
Polyalphabetism could be included later on.
I will go to the computer store in a while and at least look at some new computers.
Well, you should be fine with your current laptop I guess. If you do want a new laptop get one with the Intel i5-8250U CPU. It offers incredible price-performance and will straight up be 4 to 8 times faster than your current system.
I am currently optimizing the period + nulls & skips solver and that may take another couple of weeks. Yes, up to about 12 nulls/skips for period 15 and 19. Include the reversed directions of each period also? And remove characters (up to how many) at the end of the cipher? How many variations are we then looking at?
48 if we don’t take any suspected gibberish off of the end of the message.
Here is an update, it gets the solution 2 to 3 times as fast as the previous build and fixes some bugs: https://drive.google.com/open?id=1Fp7u2 … vAw1-AlW3w
No more need to enable the performance mode though I recommend it. The performance mode can be automatically enabled by setting "(General) Use performance mode ngrams if applicable: 1" in the settings.ini file.
I downloaded the program and am working on the 3/3 test message now. Thank you.
I downloaded the program and am working on the 3/3 test message now. Thank you.
It should solve fairly quickly but you will have to remove the 3 nulls at the end of your cipher first.
I let it run all night and did not get a solution. About 8 hours at 2.1 MIPS. I removed the last three symbols also, and set the number of nulls and skips to 6. However, I am probably doing something wrong, or it is just my computer. I re-started it and now am at work. Will see when I get home. Thanks.
I am looking into it.
I let it run all night and did not get a solution. About 8 hours at 2.1 MIPS. I removed the last three symbols also, and set the number of nulls and skips to 6. However, I am probably doing something wrong, or it is just my computer. I re-started it and now am at work. Will see when I get home. Thanks.
My solving machine gets 44 MIPS so that is where we have our difference most likely. It is a tough cipher scheme though and things get really difficult starting around 5 nulls/skips. At the moment I feel that we may not be able to test over 8 nulls/skips with confidence on the 340.
I am sure that is the difference. I just got home and no solution at 2.09 MIPS. But I will let it go all night. It will be time for me to invest in a new computer soon I can see. They aren’t very expensive, so I will start looking and planning for it. Thanks.
Would you need a new modem to go with a new computer?
Don’t know about a modem.
Here is 3/3 at 21 hours, see anything wrong besides speed?
I deleted the last 3 symbols. Does 11071 / 34898 iterations mean it is about 1 / 3 done with all possibilities?
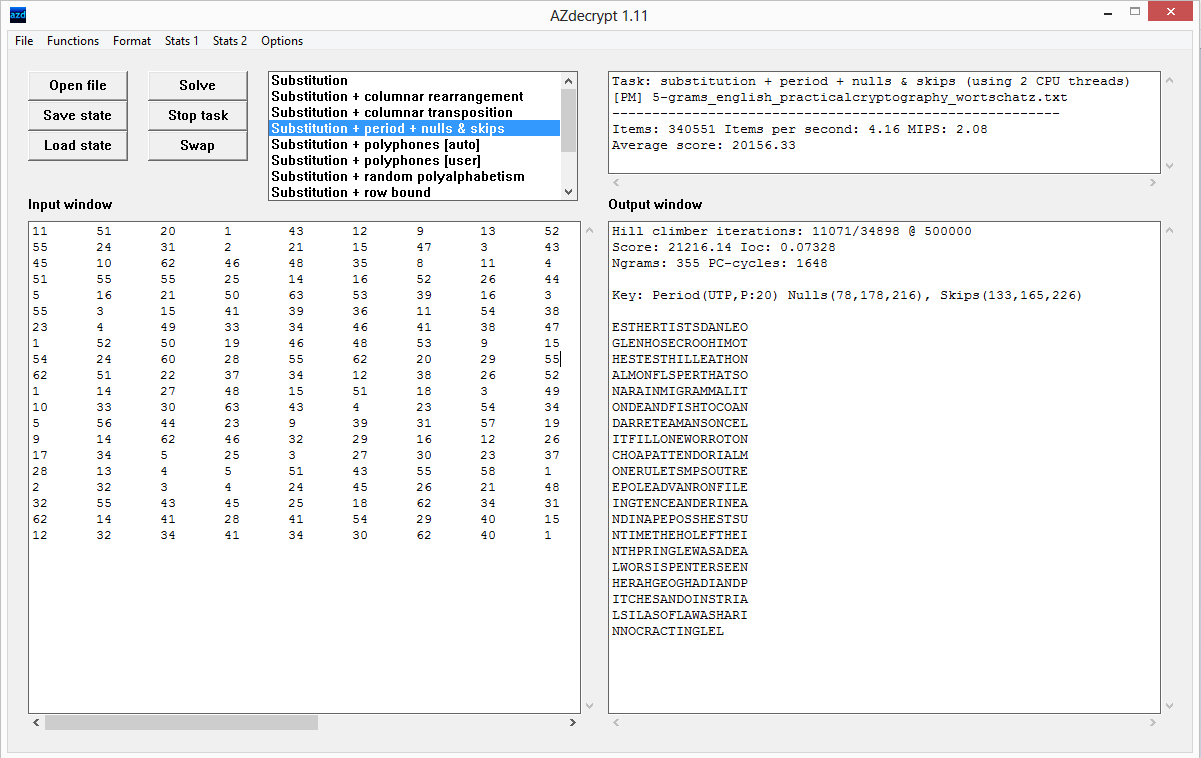
Here is 3/3 at 21 hours, see anything wrong besides speed?
Everything okay.
Does 11071 / 34898 iterations mean it is about 1 / 3 done with all possibilities?
It is the progress indicator of the current amount of hill climber iterations. It does not imply possibilities.
FYI, the output window does not only show the best result for the current amount of hill climber iterations. Check the output directory also.
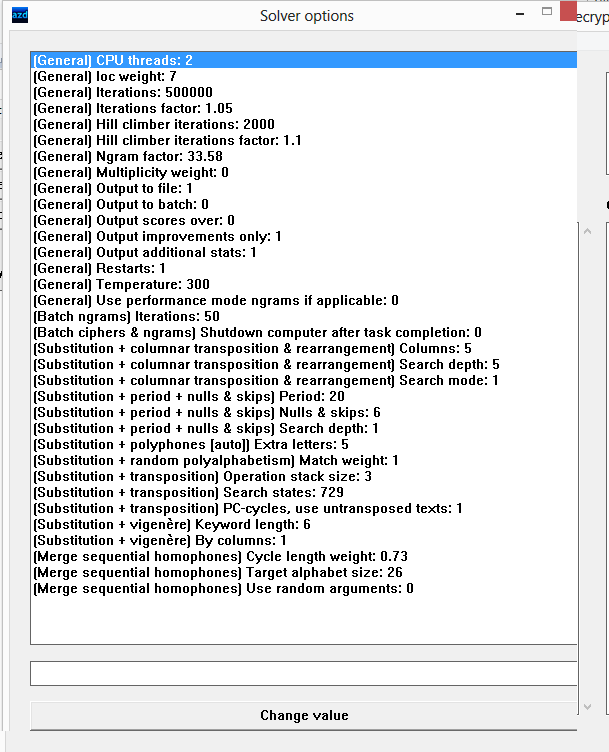
(General) Hill climber iterations: 2000 (General) Hill climber Iterations factor: 1.1
These 2 settings control the amount of hill climber iterations it throws at the problem. One iteration is usually 1 change in the key, 2000 is okay for up to 4 nulls/skips but for 5 to 6 I would recommend setting it to 10000 or 20000 to start with. The hill climber factor is the factor by which the hill climber iterations increase after it is done with the current amount. Suppose it starts with 10000, then after it is done this amount is multiplied by 1.1, 10000 times 1.1 = 11000 and so it goes on 10000, 11000, 12100, 13310 etc.
I am sure that is the difference. I just got home and no solution at 2.09 MIPS. But I will let it go all night. It will be time for me to invest in a new computer soon I can see. They aren’t very expensive, so I will start looking and planning for it. Thanks.
I am not sure about your experience with computers. When buying a laptop sellers may try to trick you in buying outdated hardware. I recommend to get one with a SDD hard drive, at least 8GB of ram and a i5-8250U or better CPU. Such a system would probably net you with something around 20 MIPS in AZdecrypt.
