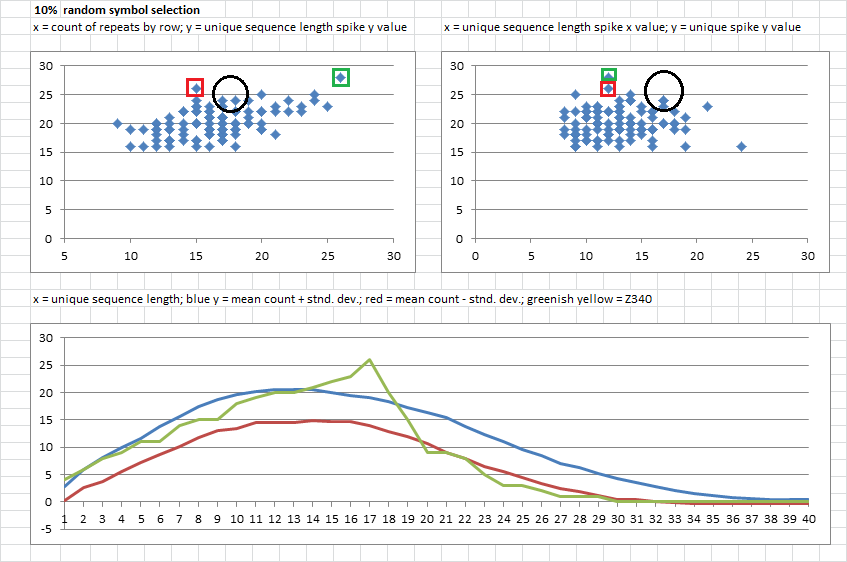
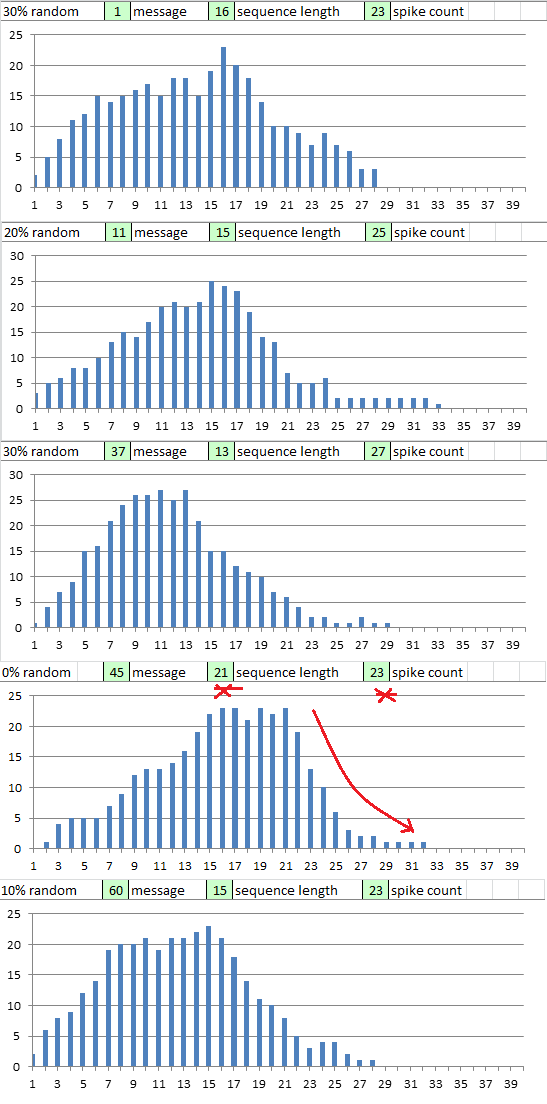
4. 10% random symbol selection. Same interpretation rules as above. Upper left and right the 340 is about in the middle with count of repeats by row, it was easy to duplicate the 340. But the spike for most except for a few was lower than for the 340. One of the messages ( red ) had 15 repeats and 26 count of unique string length of 12 ( not as long as 17 ). One of the messages ( green ) had 26 repeats, and a spike at count 28 of unique string length of 12.
Below, bell curves shift to the left of the 340 and get a little bit taller. Unique string lengths were shorter, as would be expected with some random symbol selection, and there were more of them.
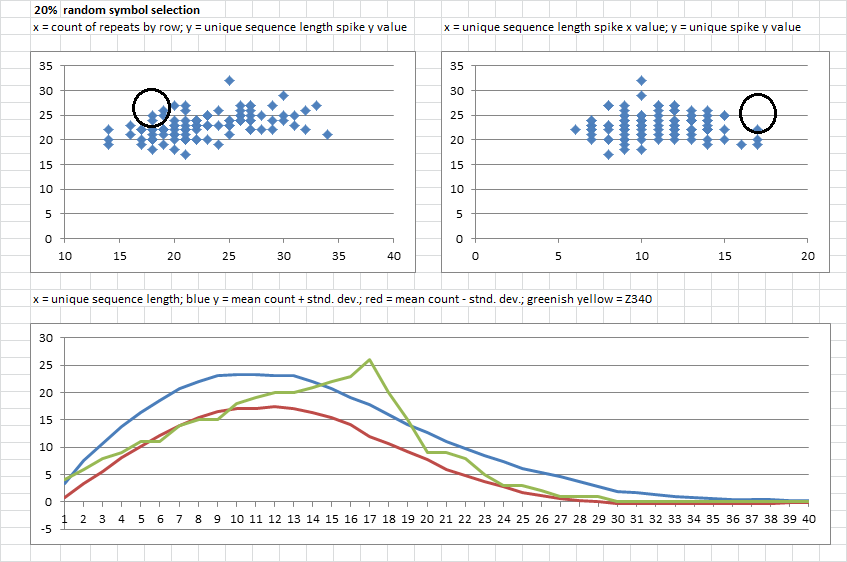
5. 20% random symbol selection. Upper left, most of the messages had higher repeats by row, which makes sense because of 20% random selection. A few of the messages had spikes higher than 26, but unique string lengths got shorter, again reflecting the 20% random selection.
Below, bell curves shift to the left again, and get taller again. Compared to the 340, unique string lengths get shorter, but the counts still do not reach 26.
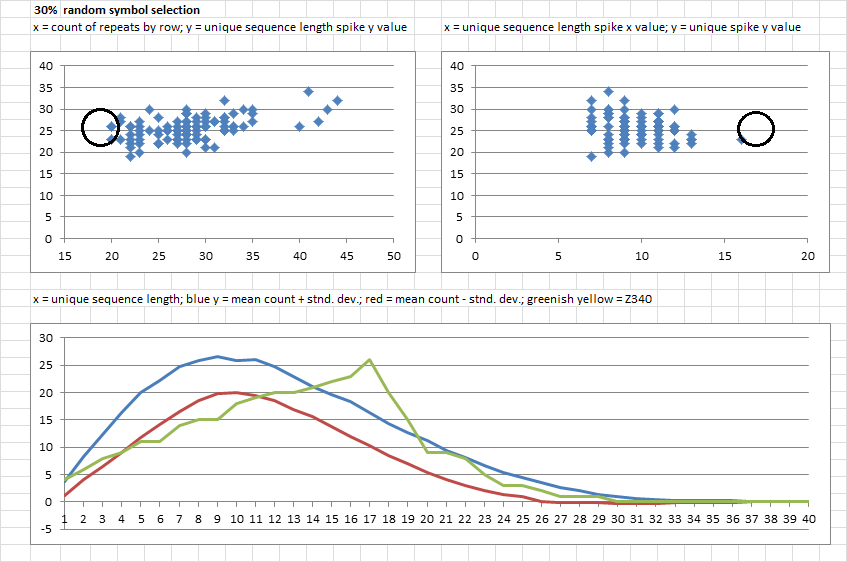
6. 30% random symbol selection. Upper left, all of the messages had more repeats by row. Upper right, unique strings lengths were all shorter than 17, and about half of the messages had spikes higher than 26.
Below, the unique string lengths got shorter and the count spikes got taller. However, the blue line should be a bit higher, so there may be some messages with really low spike counts causing a downward shift.
Conclusion: It does seem that there is some encoding mechanism at work besides just cycling homophones, and whatever is disrupting the cycles does not appear to be random symbol selection. And that slope, the sudden drop after x = 17 for the 340 may be another indicator of the mechanism.
I wonder how the start and stop positions for the unique strings of length about 17 compare with the period 19 bigram repeat symbol positions. My guess is that, since the + is highest count with 24, it is most frequently terminating unique strings. And because it is heavily represented in the period 19 repeats, I guess that those positions would match up. But I haven’t looked.
And since the + symbols avoid prime locations, I wonder if this is related somehow by chance. Maybe there is some mechanism, or some routine that he used to inadvertently cause prime phobia and the unique string length statistics.
I fully understand the calculations and your reasoning. I think you can only compare sigmas if the distribution curves are similar.
Frequencies: {0=998314, 1=1589, 2=93, 3=4} and Frequencies: {0=1694, 1=11041, 2=35718, 3=76917, 4=123054, 5=154859, 6=162316, 7=144531, 8=112690, 9=77434, 10=47950, 11=26694, 12=13797, 13=6534, 14=2873, 15=1209, 17=157, 16=449, 19=22, 18=55, 21=1, 20=4, 24=1} do not follow similar curves and cannot be directly compared to eachother.The practical value of understanding the standard deviation of a set of values is in appreciating how much variation there is from the average (mean).
Then it seems unpractical to use the standard deviation as a replacement for actual chance values (without proper normalization of some kind) because it is a tool to measure the distance from the mean given the nature of the curve.
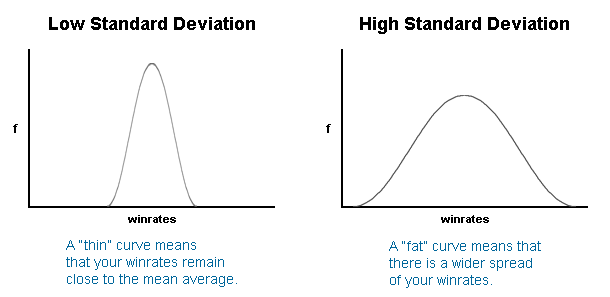
I think the fact that standard deviation is based on variance *does* have a normalizing effect when comparing two different curves. For example, we expect about 68% of samples to fall within one standard deviation of the mean, no matter if the curve is skinny or fat, because the standard deviation value will be small for the skinny curve and large for the fat curve. But, this assumes that both curves follow a normal distribution. I’m not sure what distribution the non-repeating segment counts follow. I wish we had a statistician here to help me sort this out. For now I think you are right and we should focus on chance values for the anomalous observations.
Conclusion: It does seem that there is some encoding mechanism at work besides just cycling homophones, and whatever is disrupting the cycles does not appear to be random symbol selection. And that slope, the sudden drop after x = 17 for the 340 may be another indicator of the mechanism.
I wonder how the start and stop positions for the unique strings of length about 17 compare with the period 19 bigram repeat symbol positions. My guess is that, since the + is highest count with 24, it is most frequently terminating unique strings. And because it is heavily represented in the period 19 repeats, I guess that those positions would match up. But I haven’t looked.
And since the + symbols avoid prime locations, I wonder if this is related somehow by chance. Maybe there is some mechanism, or some routine that he used to inadvertently cause prime phobia and the unique string length statistics.
Excellent analysis smokie. When I found out about the spike about 2-3 years ago I went through the same process and came to same conclusions as you. Somewhat earlier this year I experienced a small eureka moment when the observation fell into its place with the encoding hypothesis I put forward. Though it seems very likely, something else may be going on. Here is a small list.
1. Zodiac just tried not to repeat characters in a certain window, and did not cycle symbols intentionally. This creates cycles scores close to what we have observed in the 340 (depending on the window). Because there is still cycling going on due to not trying to repeat characters per window. A larger window would give rise to more cycling. It creates few unigram repeats per row and high peaks in the unique sequence lengths which drop sharply.
2. The plaintext consisted of very few unique symbols plus regular randomization of cycles. Needs further investigation, I’m not sure about this one.
3. Some sort of exotic cycling scheme which cuts the cycles short at some point.
Looking at the sequence terminators is a very good idea. Here’s the data, if I’m not mistaken then your wildcard symbol suggestions rank very highly here (perhaps due to frequency). I’m not sure about the prime phobia, the 408 also has it to quite some extent.
17: ER>pl^VPk|1LTG2dN terminator: p (2 to 18) 17: Np+B(#O%DWY.<*Kf) terminator: B (18 to 34) 17: WY.<*Kf)By:cM+UZG terminator: W (27 to 43) 17: .<*Kf)By:cM+UZGW( terminator: ) (29 to 45) 17: :cM+UZGW()L#zHJSp terminator: p (37 to 53) 17: ztjd|5FP+&4k/p8R^ terminator: F (73 to 89) 17: P+&4k/p8R^FlO-*dC terminator: k (80 to 96) 17: -*dCkF>2D(#5+Kq%; terminator: 2 (93 to 109) 17: 5+Kq%;2UcXGV.zL|( terminator: G (104 to 120) 17: V.zL|(G2Jfj#O+_NY terminator: z (115 to 131) 17: +ZR2FBcyA64K-zlUV terminator: + (142 to 158) 17: 2FBcyA64K-zlUV+^J terminator: + (145 to 161) 17: p7<FBy-U+R/5tE|DY terminator: B (164 to 180) 17: E|DYBpbTMKO2<clRJ terminator: | (177 to 193) 17: YBpbTMKO2<clRJ|*5 terminator: T (180 to 196) 17: |*5T4M.+&BFz69Sy# terminator: + (194 to 210) 17: 9Sy#+N|5FBc(;8RlG terminator: F (207 to 223) 17: Bc(;8RlGFN^f524b. terminator: c (216 to 232) 17: (;8RlGFN^f524b.cV terminator: 4 (218 to 234) 17: +yBX1*:49CE>VUZ5- terminator: + (238 to 254) 17: VUZ5-+|c.3zBK(Op^ terminator: . (250 to 266) 17: p^.fMqG2RcT+L16C< terminator: + (265 to 281) 17: CzWcPOSHT/()p|Fkd terminator: W (294 to 310) 17: T/()p|FkdW<7tB_YO terminator: B (302 to 318) 17: YOB*-Cc>MDHNpkSzZ terminator: O (317 to 333) 17: >MDHNpkSzZO8A|K;+ terminator: end of string (324 to 340) Unique sequence terminator frequencies: -------------------------------------------------- end of string: 22 (: 2 ): 7 +: 118 .: 18 2: 10 4: 13 B: 40 F: 27 G: 12 L: 1 M: 1 O: 6 R: 5 T: 6 W: 12 c: 2 k: 5 p: 25 z: 3 |: 5
Though it seems very likely, something else may be going on. Here is a small list.
1. Zodiac just tried not to repeat characters in a certain window, and did not cycle symbols intentionally. This creates cycles scores close to what we have observed in the 340 (depending on the window). Because there is still cycling going on due to not trying to repeat characters per window. A larger window would give rise to more cycling. It creates few unigram repeats per row and high peaks in the unique sequence lengths which drop sharply.
2. The plaintext consisted of very few unique symbols plus regular randomization of cycles. Needs further investigation, I’m not sure about this one.
3. Some sort of exotic cycling scheme which cuts the cycles short at some point.Looking at the sequence terminators is a very good idea. Here’s the data, if I’m not mistaken then your wildcard symbol suggestions rank very highly here (perhaps due to frequency). I’m not sure about the prime phobia, the 408 also has it to quite some extent….
Unique sequence terminator frequencies: -------------------------------------------------- end of string: 22 (: 2 ): 7 +: 118 .: 18 2: 10 4: 13 B: 40 F: 27 G: 12 L: 1 M: 1 O: 6 R: 5 T: 6 W: 12 c: 2 k: 5 p: 25 z: 3 |: 5
I agree. I need to post all of the cycle relationships in this thread. I think that the symbols that are most frequent terminators will not cycle well with other symbols.
Remember here when we first met, I identified some symbols as possible "wildcards" because they did not cycle well with other symbols. In a couple of posts on this page, I identified +, q, B, 5 and F: http://www.zodiackillersite.com/viewtop … f=81&t=267.
At least three of those are high sequence terminators listed above
In the interest of thoroughness, I looked at all 400 charts showing x axis unique sequence / string length and z axis count.
Most looked like bell curves, some were very different looking, and here are 10 that are similar to the 340.
Among others, message # 45 with perfect cycles had a unique sequence length of 21 with spike count at 23.
Among others:
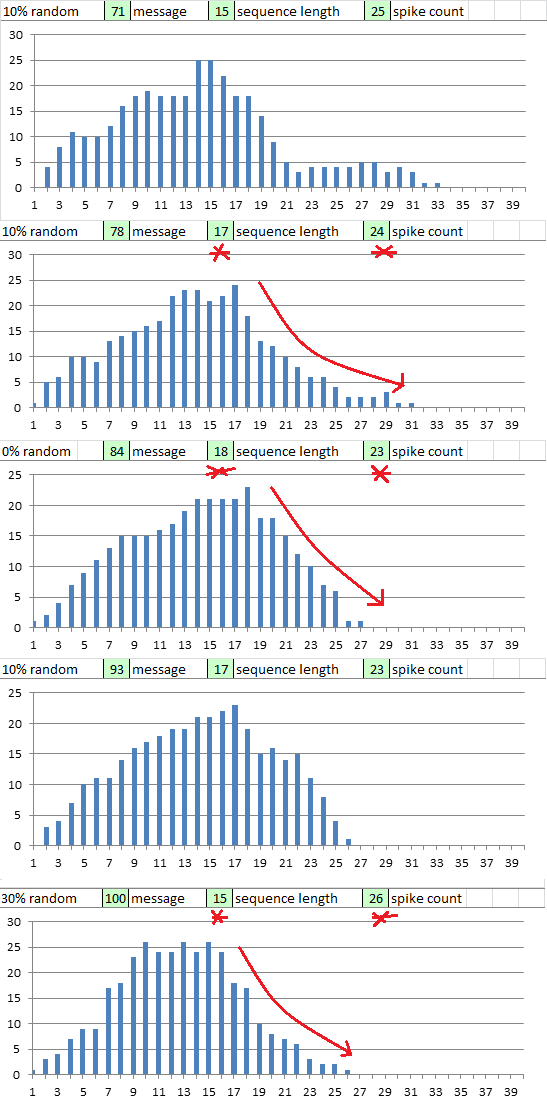
Message # 78 with 10% random selection had length of 17 with spike at 24.
Message # 84 perfect cycles had length 18 with spike at 23.
Message # 100 with 30% random selection had length 15 with spike at 26
The 340 seems to be at the margins, in a small group of messages with unique sequence length and similar spike count, and with a similar slope to the right of the spike.
OK I ran an experiment with ten million shuffles each of z340 and z408. Here are the results, sorted from most significant to least significant.
Columns are: Non-repeating segment length, number of occurrences in the actual cipher, number of times the same count appeared in 10,000,000 shuffles of the cipher
z408:
24 9 2 25 8 3 23 10 8 27 6 9 21 12 12 26 6 34 32 3 39 22 10 111 28 4 207 7 20 322 33 2 328 30 3 349 29 3 955 34 1 2528 8 23 4696 4 14 4910 5 18 5149 6 21 5332 3 10 7921 19 11 24840 31 1 33734 20 8 64893 2 8 103586 18 11 148777 17 13 207813 9 27 237130 10 26 475808 16 14 500387 1 5 710567 13 22 913864 12 22 998208 11 26 1036219 15 14 1087550 14 17 1089015
Is it interesting that segment length 24’s count of 9 occurs so rarely during shuffles? 24 happens to coincide with the total height of z408.
z340:
17 26 0 18 20 1 6 11 3 7 14 48 16 23 62 19 15 68 5 11 95 8 15 137 4 9 374 9 15 502 22 8 1092 21 9 1755 15 22 2959 3 8 7059 20 9 11545 23 5 20857 25 3 59653 2 6 61334 14 21 72623 10 18 112278 24 3 145307 26 2 168308 29 1 217333 28 1 389986 13 20 596968 27 1 668957 11 19 769939 1 5 1075177 12 20 1186750
It’s interesting that the smaller segment lengths (such as 6 and 7) are also showing counts that occur so rarely during shuffles. Didn’t you notice something like that before, Jarlve? Something to do with shorter segment lengths? The way the numbers turned out feels related to how the cipher is split in halves if you consider the non-repeats in rows 1,2,3 and rows 11,12,13.
The 340 seems to be at the margins, in a small group of messages with unique sequence length and similar spike count, and with a similar slope to the right of the spike.
Possibly the 340 is also such an outlier but there is still quite a bit of difference. Given the estimated randomization in the cycles, a peak at 17, 26 is still very high. While a peak at 15, 26 may seem close it is not. Also, unigram repeats per row.
Frequencies from 10.000.000 randomizations: 15, 26: 40 17, 23: 3 (highest observed)
Is it interesting that segment length 24’s count of 9 occurs so rarely during shuffles? 24 happens to coincide with the total height of z408.
Here is a part of my list for the 408. Seems fine to me.
23, 1: 2952593 23, 2: 1097061 23, 3: 335211 23, 4: 89542 23, 5: 21889 23, 6: 5004 23, 7: 1073 23, 8: 224 23, 9: 40 23, 10: 4 24, 1: 2257645 24, 2: 589066 24, 3: 132819 24, 4: 27515 24, 5: 5151 24, 6: 935 24, 7: 159 24, 8: 35 24, 9: 5 25, 1: 1531181 25, 2: 288692 25, 3: 49476 25, 4: 7965 25, 5: 1226 25, 6: 175 25, 7: 17 25, 8: 3
It’s interesting that the smaller segment lengths (such as 6 and 7) are also showing counts that occur so rarely during shuffles. Didn’t you notice something like that before, Jarlve? Something to do with shorter segment lengths?
As smokie pointed out, it looks like a bell curve. The reason why counts of shorter sequences are rare is because shorter sequences per cipher are quite common. Look at the following part.
2, 1: 3 2, 2: 40 2, 3: 283 2, 4: 1445 2, 5: 5651 2, 6: 18084 2, 7: 46600 2, 8: 103896 2, 9: 198299 2, 10: 338181 2, 11: 513737 2, 12: 706821 2, 13: 884815 2, 14: 1019604 2, 15: 1081340 2, 16: 1068485 2, 17: 978450 2, 18: 839788 2, 19: 677484 2, 20: 515205 2, 21: 368925 2, 22: 250168 2, 23: 161532 2, 24: 98364 2, 25: 57640 2, 26: 31847 2, 27: 16948 2, 28: 8613 2, 29: 4183 2, 30: 2026 2, 31: 874 2, 32: 389 2, 33: 172 2, 34: 78 2, 35: 21 2, 36: 8 2, 37: 1
A sequence of 2, 1 would look like this "121", now imagine there’s only one of that in the entire cipher. Following the list, very roughly, on average, there are about 15 sequences with a length of 2 per cipher.
The way the numbers turned out feels related to how the cipher is split in halves if you consider the non-repeats in rows 1,2,3 and rows 11,12,13.
My opinion on that observation is that it is most likely a coincidence. We have looked at reasoning that a secondary encoding starts at 11 (or any split for that matter), we didn’t find it. The only thing that then remains is to consider what Olson has stated, that only these lines somehow contain the message. Which I can’t reconcile with the findings of periodical bigram repeats.
Is it interesting that segment length 24’s count of 9 occurs so rarely during shuffles? 24 happens to coincide with the total height of z408.
Here is a part of my list for the 408. Seems fine to me.
Thanks for posting your numbers. The sigma for length 24 occurring 9 times in z408, which only happened twice in my 10,000,000 shuffles, comes out to about 10,062 if I did the math right. Do you think it’s just because of the normal cycling going on in z408 which naturally increases the lengths of non-repeating segments?
My opinion on that observation is that it is most likely a coincidence. We have looked at reasoning that a secondary encoding starts at 11 (or any split for that matter), we didn’t find it. The only thing that then remains is to consider what Olson has stated, that only these lines somehow contain the message. Which I can’t reconcile with the findings of periodical bigram repeats.
It still seems unusual to me that in z340, there are 11 occurrences of non-repeating segments of length 6, when only 3 out of 10,000,000 shuffles showed that same count. That works out to a sigma of about 6,700. Whereas in z408, there is no similar bias towards smaller non-repeating segment lengths.
Here is my spreadsheet showing all the results: https://docs.google.com/spreadsheets/d/ … sp=sharing The first tab shows all the segment lengths for each cipher sorted by decreasing significance when compared to shuffles. The second tab summarizes all the counts found during the 10,000,000 shuffles.
Also, I ran another experiment that shuffles the cipher until a count of 26 or higher is achieved for non-repeating segment length 17. At around 1.9 million shuffles, it encountered a count of 25 for length 17, but it just passed 600 million shuffles and still hasn’t encountered a count of 26. Very rare indeed!
Thanks for posting your numbers. The sigma for length 24 occurring 9 times in z408, which only happened twice in my 10,000,000 shuffles, comes out to about 10,062 if I did the math right. Do you think it’s just because of the normal cycling going on in z408 which naturally increases the lengths of non-repeating segments?
Yes, it is a bell curve which grows more wide with increased cycling. So the segments grow longer but the repeat counts go down.
It still seems unusual to me that in z340, there are 11 occurrences of non-repeating segments of length 6, when only 3 out of 10,000,000 shuffles showed that same count. That works out to a sigma of about 6,700. Whereas in z408, there is no similar bias towards smaller non-repeating segment lengths.
I see what you mean, you may be on to something. Or, it is just the bell curve at work. For example if there are many longer segments then there will be less room for shorter segments. Nice spreadsheet, I love it. I see that the sigma values have changed for the better, what did you do? I’m guessing you used the occurrences per 10.000.000 randomizations?
Also, I ran another experiment that shuffles the cipher until a count of 26 or higher is achieved for non-repeating segment length 17. At around 1.9 million shuffles, it encountered a count of 25 for length 17, but it just passed 600 million shuffles and still hasn’t encountered a count of 26. Very rare indeed!
Okay that made my day, not a single occurrence in 600.000.000 randomizations. That is just cool.
I see what you mean, you may be on to something. Or, it is just the bell curve at work. For example if there are many longer segments then there will be less room for shorter segments.
Yes, that’s true – also, the segment finding approach we are using is a "greedy" approach, since it prefers to find the maximal non-repeating segment at each position under consideration, rather than overcounting the shorter segments it consists of.
Nice spreadsheet, I love it. I see that the sigma values have changed for the better, what did you do? I’m guessing you used the occurrences per 10.000.000 randomizations?
That’s correct. Previously, the sigma was computed on the counts themselves. The current method is to instead compute sigma on the number of occurrences of each count. I still don’t understand why the previous method seems intuitively wrong based on the fact that a count of 26 for segment length 17 is so improbable despite the prediction of standard deviation.
Also, I ran another experiment that shuffles the cipher until a count of 26 or higher is achieved for non-repeating segment length 17. At around 1.9 million shuffles, it encountered a count of 25 for length 17, but it just passed 600 million shuffles and still hasn’t encountered a count of 26. Very rare indeed!
Okay that made my day, not a single occurrence in 600.000.000 randomizations. That is just cool.
Agreed. Your discovery is very statistically significant!
The way the numbers turned out feels related to how the cipher is split in halves if you consider the non-repeats in rows 1,2,3 and rows 11,12,13.
Before I understood what you were talking about I tried to redraft the message into even numbers of columns, then check the left half cycles and right half cycles, and I stacked the left half on top of the right half and checked those cycle scores also.
The scores are generally lower than by reading the message left right top bottom 17 columns. That is not what he did.
Here is a message with perfect palindromic cycles if anyone wants to check it. Otherwise I can check it when I get home. The cycle scores are a little bit lower than the 340, but not by much.
22 28 23 26 11 27 24 29 30 25 34 18 42 12 38 43 31
13 5 14 7 1 54 46 15 24 50 23 47 48 39 32 55 8
20 16 54 35 22 51 22 49 33 40 44 14 17 54 34 52 21
2 37 26 23 30 29 24 36 19 58 25 28 9 18 3 32 13
24 35 53 20 12 16 41 45 44 11 48 52 6 11 7 4 55
47 12 32 3 34 23 46 51 20 13 33 40 46 50 10 2 34
18 14 44 39 54 47 1 35 22 32 1 28 38 16 2 29 30
50 38 26 22 31 30 48 39 32 15 51 21 23 36 19 18 24
56 14 49 33 13 52 20 12 32 40 48 53 52 20 45 25 29
28 24 37 18 11 60 42 11 44 12 36 7 13 23 51 22 47
14 57 15 35 5 14 50 50 13 44 51 21 3 34 19 12 52
53 22 34 18 61 41 54 45 44 40 8 27 46 39 17 16 59
23 52 20 4 18 24 44 28 51 20 11 5 11 46 50 42 3
45 50 38 16 25 51 24 47 52 21 2 53 58 20 12 35 23
9 22 13 22 58 23 29 30 6 14 44 15 5 38 44 36 24
37 43 1 45 1 9 25 7 14 2 36 10 3 31 30 52 20
13 24 21 4 56 12 26 23 29 28 11 9 59 22 28 29 5
11 7 39 32 12 33 62 48 30 3 56 13 49 22 58 23 31
30 35 40 51 19 24 57 14 61 41 55 32 61 34 2 32 15
6 14 8 1 54 48 13 62 40 54 58 25 29 28 50 44 61
Yes, that’s true – also, the segment finding approach we are using is a "greedy" approach, since it prefers to find the maximal non-repeating segment at each position under consideration, rather than overcounting the shorter segments it consists of.
Indeed. Another alteration would be to accept segments with x amount of repeats.
Here is a message with perfect palindromic cycles if anyone wants to check it.
Thanks allot for your cipher. The curve peaks at 7 and then drops down and goes slightly up again for a second peak at 17. Randomization of cycles is on par with the 340. I think we all need to revise our measurements and such for different types of cycles. And the nature of the plaintext also needs to be taken in account. There’s allot of work here.

I don’t know if it is a fair thing to do, but removing some of the most frequent segment terminators does shift the peak to 16 or 15. Here’s how it looks after removing the "+" symbol. It is spread very equally around the cipher and especially the midpoint. So I wonder if there is a connection between that and the abnormally high peak at 17. doranchak how do your L2 and L3 perfect cycles measurement look for smokie’s cipher versus the 340?
Unique sequence frequencies: -------------------------------------------------- Length 1: 2 Length 2: 3 Length 3: 4 Length 4: 5 Length 5: 6 Length 6: 5 Length 7: 6 Length 8: 9 Length 9: 11 Length 10: 13 Length 11: 15 Length 12: 16 Length 13: 17 Length 14: 21 Length 15: 21 Length 16: 25 <--- Length 17: 24 Length 18: 19 Length 19: 16 Length 20: 17 Length 21: 15 Length 22: 10 Length 23: 8 Length 24: 9 Length 25: 8 Length 26: 4 Length 27: 4 Length 28: 3
After removing top 4 most frequent segment terminators "+, B, F, p".
Unique sequence frequencies: -------------------------------------------------- Length 1: 1 Length 2: 2 Length 3: 3 Length 4: 3 Length 5: 4 Length 6: 3 Length 7: 6 Length 8: 6 Length 9: 9 Length 10: 10 Length 11: 13 Length 12: 11 Length 13: 12 Length 14: 17 Length 15: 22 <--- Length 16: 18 Length 17: 15 Length 18: 20 <--- (secondary peak) Length 19: 18 Length 20: 16 Length 21: 16 Length 22: 13 Length 23: 12 Length 24: 7 Length 25: 6 Length 26: 5 Length 27: 3 Length 28: 3 Length 29: 2 Length 30: 1 Length 31: 1 Length 32: 1 Length 33: 1 Length 34: 1 Length 35: 1 Length 36: 1
Top and bottom halves compared, both peak at 17. I did a sliding through analysis once with a window of 10 rows and almost all parts peaked at 17. In other words, the phenomena is very equally spread throughout the cipher.
I am actually a little bit excited by palindromic cycles.
The message above was like this: 1 2 3 4 3 2 1 1 2 3 4 3 2 1 1 2 3 4 3 2 1.
EDIT: Message deleted. I will work on some like this 1 2 3 4 3 2 1 2 3 4 3 2 1, which should shift the spike to the right. I have to re-tool my encoder.