O.k the first palindromic message was lame, but here is a better one. Before I went like this: 1 2 3 4 3 2 1 1 2 3 4 3 2 1 1 2 3 4 3 2 1 etc.
Now this one is perfect cycles and goes like this: 1 2 3 4 3 2 1 2 3 4 3 2 1. I didn’t repeat the first symbol, which makes a big difference.
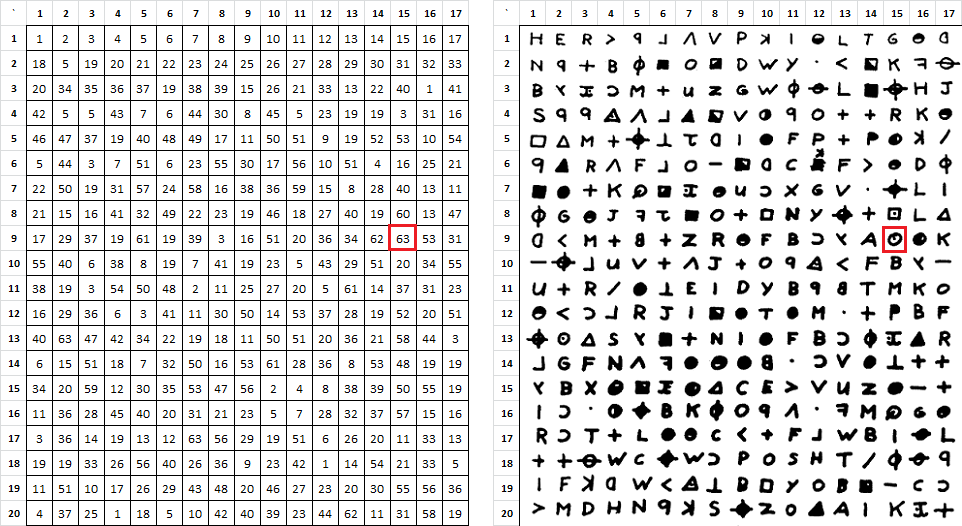
It is I like killing and here is the key:
A 1 2 3 4 3 2
B 5 6
C 7 8
D 9 10
E 11 12 13 14 15 14 13 12
F 16 17
G 18 19
H 20 21
I 22 23 24 25 24 23
J
K 26 27
L 28 29 30 31 30 29
M 32 33
N 34 35 36 37 36 35
O 38 39 40 41 40 39
P 42 43
Q
R 44 45
S 46 47 48 49 48 47
T 50 51 52 53 52 51
U 54 55
V 56 57
W 58 59
X 60
Y 61 62
Z
Here is the message. The spike shifts to the right and is in the ballpark with the 340 stats.
22 28 23 26 11 27 24 29 30 25 34 18 42 12 38 43 31
13 5 14 7 1 54 46 15 24 50 23 47 48 39 32 55 8
20 16 54 35 22 51 23 49 33 40 44 14 17 55 36 52 21
2 37 26 24 30 29 25 36 19 58 24 28 9 18 3 32 13
23 35 53 20 12 16 41 45 44 11 48 52 6 12 7 4 54
47 13 33 3 34 22 46 51 21 14 32 40 47 50 10 2 35
19 15 45 39 55 48 1 36 23 33 2 29 38 17 3 30 31
51 39 27 24 30 29 49 40 32 14 52 20 25 37 18 19 24
56 13 48 33 12 53 21 11 32 41 47 52 51 20 44 23 28
29 22 36 18 12 60 42 13 45 14 35 8 15 23 50 24 46
14 57 13 34 5 12 51 52 11 44 53 21 4 35 19 12 52
51 25 36 18 61 40 54 45 44 39 7 26 47 38 16 17 59
24 50 20 3 19 23 45 30 51 21 13 6 14 48 52 43 2
44 53 39 16 22 52 23 49 51 20 1 50 58 21 15 37 24
9 25 14 24 59 23 31 30 5 13 45 12 6 40 44 36 22
35 42 2 45 3 10 23 8 11 4 34 9 3 29 28 51 20
12 24 21 2 56 13 27 25 29 30 14 10 58 24 31 30 5
15 7 41 33 14 32 62 48 29 1 57 13 47 23 59 22 28
29 35 40 52 18 23 56 12 61 39 55 33 62 36 2 32 11
6 12 8 3 54 46 13 61 38 55 58 24 30 31 53 44 62
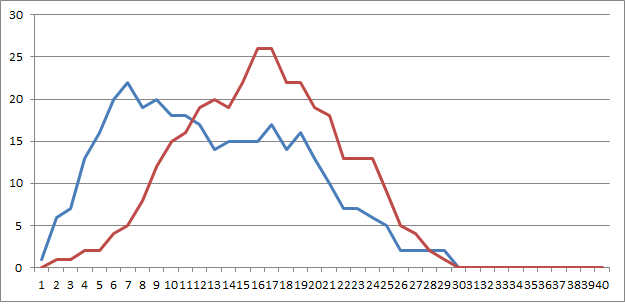
EDIT: Here is what making that subtle change not repeating the first symbol in the cycle does. First lame message is blue, new better message is red and puts us exactly where we need to be with spike.
Hey smokie,
Here’s a comparison between your latest palindromic and the 340 with the "+" symbol removed. I think that it is fair since your cipher does not have such a high frequency symbol. The graphs are a very good match, though the randomization in the cycles is less than in the 340. Bottom line: we need to come up with a test for exotic cycles.

Yes, that’s true – also, the segment finding approach we are using is a "greedy" approach, since it prefers to find the maximal non-repeating segment at each position under consideration, rather than overcounting the shorter segments it consists of.
Indeed. Another alteration would be to accept segments with x amount of repeats.
I am running this alteration now, for both z340 and z408, with x ranging from 1 to 4, and comparing to 10,000,000 shuffles each.
doranchak how do your L2 and L3 perfect cycles measurement look for smokie’s cipher versus the 340?
Here are the comparisons of various cycle-related measurements:
jarlve non-repeat score #1
z340: 4462
smokie palindromic 1: 4335
smokie palindromic 2: 5544
jarlve non-repeat score #2
z340: 1599
smokie palindromic 1: 1597
smokie palindromic 2: 1617
perfect cycle score L=2
z340: 247.85
smokie palindromic 1: 236.41
smokie palindromic 2: 525.00
perfect cycle score L=3
z340: 62.36
smokie palindromic 1: 71.48
smokie palindromic 2: 205.32
jarlve m_2s_cycles
z340: 2150.72
smokie palindromic 1: 2203.52
smokie palindromic 2: 2880.54
Thanks doranchak,
I’ve been looking at the distances between symbols and that these may be related to the encoding. While I was trying to distinguish between palindromic and randomization I stumbled upon another weird thing in the 340. If you square all the distances between the symbols and total it you will find that the 340 scores very highly compared to other ciphers. Here is why.

On average, less frequent symbols will show a greater distance between each other than more frequent occurring symbols, but why is this such a default thing in the 340 with top-bottom symmetry to boot?
AZdecrypt distance stats for: 340.txt -------------------------------------------------- H: 66078 (4) <--- E: 35666 (3) R: 12336 (8) >: 37150 (4) p: 17500 (11) l: 14012 (7) ^: 14487 (6) V: 13610 (6) P: 52565 (3) k: 51030 (5) <--- |: 14328 (10) 1: 54196 (3) <--- L: 26794 (6) T: 35882 (5) G: 18582 (6) 2: 9880 (9) d: 35535 (5) N: 30046 (5) +: 7538 (24) B: 16502 (12) (: 17412 (7) #: 11235 (5) O: 13230 (10) %: 6889 (2) D: 33318 (4) W: 58668 (6) <--- Y: 31779 (4) .: 16406 (6) <: 22402 (6) *: 20443 (6) K: 17596 (7) f: 20571 (4) ): 58893 (5) <--- y: 15669 (5) :: 42849 (2) <--- c: 11591 (10) M: 15996 (7) U: 13612 (5) Z: 28643 (4) z: 11385 (9) J: 7652 (4) S: 33761 (4) 7: 34004 (3) 8: 31755 (4) 3: 39204 (2) _: 38569 (3) 9: 10918 (4) t: 20088 (4) j: 2500 (2) 5: 7303 (7) F: 8607 (10) &: 14400 (2) 4: 8026 (6) /: 24562 (3) -: 15522 (5) C: 24870 (5) q: 26569 (2) ;: 26500 (3) X: 16384 (2) @: 0 (1) b: 4068 (3) A: 34596 (2) 6: 8354 (3) Total: 1470516
Yes, that’s true – also, the segment finding approach we are using is a "greedy" approach, since it prefers to find the maximal non-repeating segment at each position under consideration, rather than overcounting the shorter segments it consists of.
Indeed. Another alteration would be to accept segments with x amount of repeats.
I am running this alteration now, for both z340 and z408, with x ranging from 1 to 4, and comparing to 10,000,000 shuffles each.
OK, this experiment is complete. The full results are combined in the first tab here, in descending order of statistical significance:
https://docs.google.com/spreadsheets/d/ … sp=sharing
When "max repeats allowed" is zero, no symbols are allowed to repeat in the segment. When it is 1, only 1 symbol is allowed to repeat. When it is 2, only 2 symbols are allowed to repeat. Etc.
The peak of 26 at length 17 for Z340 with max repeats 0 is the only observation of Z340’s segments that never occurred in any of the 10,000,000 shuffles of Z340. A handful of segments of Z408 with max repeats > 0 also never occurred in any of the 10,000,000 shuffles of Z408.
Segment length 24 for Z408 with max repeats 0 was previously the most significant segment I found among another set of 10,000,000 shuffles, but this time it was beaten by segment length 25.
The other thing I was curious about was if it was possible to exactly calculate the probability that a given segment length with occur a specific number of times. What is the probability that non-repeating segment of length 17 will occur 26 times in Z340? First I looked at the probability of a single segment of length 17 occurring with no repeated symbols. There are 324 ways a segment of length 17 can be considered in Z340. For 323 of them, the segment has to be terminated (at the 18th position) by a symbol that has already been seen. For the 324th (last) segment, it does not have to be terminated. I did not calculate the exact probabilities but empirically computed them based on 10,000,000 shuffles. The result is 0.0192633 for the first 323 positions, and 0.0642 for the last position.
So, now you can calculate the probability that zero non-repeating segments of length 17 were observed. It is (1 – 0.0192633) ^ 323 * (1 – 0.0642) = 0.0017483. For 10,000,000 shuffles, this would work out to 17483. In my actual experiments, the result was 17006, so this probability calculation seems accurate.
What is the probability of only 1 non-repeating segment of length 17 being observed? It could occur in position 1. Or position 2. Or position 3. Etc. Probability of it appearing in position 1 is 0.0192633 times the probability that all the other positions did not produce any segment of length 17. This is equal to 0.0192633 * ((1 – 0.0192633) ^ 322) * (1 – 0.0642). But now we also have to add the probability that it happened at position 2, or position 3, etc. Therefore the the probability of only 1 non-repeating segment of length 17 being observed is 323 * 0.0192633 * ((1 – 0.0192633) ^ 322) * (1 – 0.0642) + 0.0642 * ((1 – 0.0192633) ^ 323) = 0.0112116. So we estimate that for 10,000,000 shuffles, we’d find 112116 shuffles that have exactly one segment of length 17 being observed. In my actual experiments, the result is 110943, so we seem to be on the right track.
Now what’s the probability of only 2 non-repeating segments of length 17 being observed? Now we can have 2 segments appearing somewhere in the first 323 positions (situation #1). Or, we can have one segment appearing in position 324 and the other appearing somewhere in the first 323 positions (situation #2). This means we have to add more possibilities to the calculation. Namely, there are (323 choose 2) ways for the 2 segments to appear for situation #1, and (323 choose 1) for situation #2 to happen. Now we can generalize the probability formula: p = (323 choose k) * (0.0192633 ^ k) * ((1 – 0.0192633) ^ (323 – k)) + 0.0642 * (323 choose k – 1) * (0.0192633 ^ (k – 1)) * ((1 – 0.0642) ^ (324 – k), where k is the number of occurrences.
Here is the resulting probability table computed for k=1 through k=29 for z340 length 17. The columns are: k, estimated probability, expected occurrences per 10,000,000 shuffles, actual occurrences per 10,000,000 shuffles, error percentage:
1 0.01197257315 119725.7315 110943 7.34% 2 0.03824260867 382426.0867 360452 5.75% 3 0.08117997298 811799.7298 772866 4.80% 4 0.1288369085 1288369.085 1225993 4.84% 5 0.1630596379 1630596.379 1548553 5.03% 6 0.1714321356 1714321.356 1620766 5.46% 7 0.1539955017 1539955.017 1446047 6.10% 8 0.1206548215 1206548.215 1125543 6.71% 9 0.0837601668 837601.668 773544 7.65% 10 0.05216479729 521647.9729 479149 8.15% 11 0.02943915415 294391.5415 267597 9.10% 12 0.01518031923 151803.1923 138555 8.73% 13 0.007202222151 72022.22151 65690 8.79% 14 0.003162680683 31626.80683 28458 10.02% 15 0.001292006209 12920.06209 11834 8.41% 16 4.93E-04 4932.016049 4550 7.75% 17 1.77E-04 1766.161617 1643 6.97% 18 5.95E-05 595.365241 551 7.45% 19 1.90E-05 189.505436 190 -0.26% 20 5.71E-06 57.11435834 54 5.45% 21 1.63E-06 16.33943349 8 51.04% 22 4.45E-07 4.447112989 4 10.05% 23 1.15E-07 1.15388494 4 -246.66% 24 2.86E-08 0.285961258 0 100.00% 25 6.78E-09 0.06780508721 0 100.00% 26 1.54E-09 0.01540701597 0 100.00% 27 3.36E-10 0.003359806052 0 100.00% 28 7.04E-11 7.04E-04 0 100.00% 29 1.42E-11 1.42E-04 0 100.00%
Long story short: Based on these estimates, we would expect about 1 in every 650,000,000 shuffles to produce a peak of 26 for segment length 17.
I’m interested in deriving the exact probabilities to replace the empirical probabilities 0.0192633 and 0.0642, but it might take a lot of work. You have to count the total number of possible length 17 strings. Then count the number of those that have no repeating symbols, then calculate the ratio. I lack the stamina to complete that task. ![]()
Long story short: Based on these estimates, we would expect about 1 in every 650,000,000 shuffles to produce a peak of 26 for segment length 17.
Thanks for your analysis doranchak. It’s interesting that the 408 also has very rare segments when allowing x amount of repeats. I wonder now if summing up the segment lengths to arrive for instance at 4462 for the 340 is a good scoring method since it only seems to calculate the surface area. What do you think? If not, then what could work as an approximation considering different ciphers?
Bottom line: we need to come up with a test for exotic cycles.
I’ve been revisiting the idea of using a "longest repeating substring" (LRS) search to locate repeating patterns involving sets of symbols. The problem with LRS, however, is that it produces numerous spurious results, because longer repeating sequences might seem rare but actually belong to an enormous space of possible patterns that could have turned up at random.
Anyway, since my search no longer restricts patterns to the "perfect cycle" variety, a few interesting ones turn up for Z340. Here are some patterns that repeat perfectly 3 times within the strings that result when you remove every other symbol:
K/DK; — DK [K/DK;] [K/DK;] [K/DK;]
DKZK/ — [DKZK/] [DKZK/] [DKZK/] DZK
DKfZK — [DKfZK] [DKfZK] [DKfZK] fDZK
*B6BtB — B*B*t [*B6BtB] [*B6BtB] [*B6BtB] B*
RDYR4 — [RDYR4] [RDYR4] [RDYR4] R444RYD
Note that this was an L=4 search but the LRS method discovers patterns that are longer than 4 in length.
I don’t know yet if the patterns are statistically significant (my hunch is that they are not). It may require many randomization experiments on the substrings under consideration, to see how often patterns with the same length repeat with the same frequency.
Also, I should be able to modify the LRS method to discover palindromic cycles. And I thought of another kind of cycle repeat pattern: ABC BCA CAB ABC (in each repeat, the sequence is shifted on position to the right). Maybe someone already mentioned that possibility.
I did an L=5 search and these are interesting, because they repeat perfectly:
f:Z3fZA — [f] [f]
^Y^3^qYA — [^Y^3^qYA] [^Y^3^qYA]
^D*^*3^*DA — [^D*^*3^*DA] [^D*^*3^*DA]
Note that when I use LRS, L=5 now means the alphabet size is 5 rather than the repeating pattern’s length.
Thanks for all of the hard work, doranchak and Jarlve. I plan to work on the idea of palindromic or other unique cycles as well.
With smokie palindromic 2, there are only 8 palindromic cycles. The others have only two symbols and are perfect L=2 cycles. I wonder if it is possible to find true palindromic or unique cycles amongst all of the possibilities. Perhaps reading the message right left bottom top as well as left right top bottom may help because the true cycles may show up first. Doranchak, maybe see what happens when you look at smokie palindromic 2.
I will think of a model that incorporates a high count symbol like the +. There are other considerations with the +, especially the fact that the + is heavily represented in the period 15 / 19 bigram repeats. I tried to make transposition / cyclic messages in an experiment some time ago, and it may be posted in the Homophonic Substitutions thread but I would have to look for it. I made the messages and randomly inserted 24 nulls which could also be 1:1 substitutes. The 24 symbols were not heavily represented in the period 15 / 19 repeats. Anyway, just thinking of a model that will replicate what we are observing.
I don’t know if this type of measurement would be useful, but if you have 1 2 3 4 3 2 1 2 3 4 3 2 1, the 2’s would be closer together and then farther apart. And the 3’s would be closer together and then farther apart. Maybe for each symbol, find the positions and the distances between each, alternating distances. If the odd distances are generally smaller than the even distances, or vice versa, generally for some symbols, then maybe the measurements all added up would be different than for perfect regular cycles. Jarlve, you probably already thought of something like that.
Thanks for your analysis doranchak. It’s interesting that the 408 also has very rare segments when allowing x amount of repeats. I wonder now if summing up the segment lengths to arrive for instance at 4462 for the 340 is a good scoring method since it only seems to calculate the surface area. What do you think? If not, then what could work as an approximation considering different ciphers?
Good question – I’d have to think about this for a while. Your segment addition scores are still useful for detecting when the encoding method is causing symbols to spread apart more than they would if they were selected randomly. But to refine it further to detect the presence of anomalous statistically significant segments would require either a direct way to compute the probabilities of each observed segment, or a comparison to shuffles. Shuffles would slow down the measurement process quite a bit. A direct computation of the probabilities might also be slow due to complex combinatorics sometimes involved in counting up all the possibilities for symbol placements.
I’ve been revisiting the idea of using a "longest repeating substring" (LRS) search to locate repeating patterns involving sets of symbols. The problem with LRS, however, is that it produces numerous spurious results, because longer repeating sequences might seem rare but actually belong to an enormous space of possible patterns that could have turned up at random.
I like to count alternations while sliding through the cycle. For example "123123", compare 1 with 2, compare 1 with 3 and compare 2 with 3 (if all unique then it’s 1 alternation) and then increment position and repeat. Normalization by cycle length also seems useful since homophonic substitution supresses frequencies. For example, a 3 symbol cycle would expect to take up about 16 symbols in the 340 (340/63*3).
Also, I should be able to modify the LRS method to discover palindromic cycles. And I thought of another kind of cycle repeat pattern: ABC BCA CAB ABC (in each repeat, the sequence is shifted on position to the right). Maybe someone already mentioned that possibility.
The offset cycle. Haven’t seen it mentioned, good idea.
I did an L=5 search and these are interesting, because they repeat perfectly:
f:Z3fZA — [f] [f]
^Y^3^qYA — [^Y^3^qYA] [^Y^3^qYA]
^D*^*3^*DA — [^D*^*3^*DA] [^D*^*3^*DA]Note that when I use LRS, L=5 now means the alphabet size is 5 rather than the repeating pattern’s length.
Here the length of the pattern is longer than the isnpected cycle size. I suspect that it could summon up returns which consist of 2 or more individual cycles.
I will think of a model that incorporates a high count symbol like the +. There are other considerations with the +, especially the fact that the + is heavily represented in the period 15 / 19 bigram repeats. I tried to make transposition / cyclic messages in an experiment some time ago, and it may be posted in the Homophonic Substitutions thread but I would have to look for it. I made the messages and randomly inserted 24 nulls which could also be 1:1 substitutes. The 24 symbols were not heavily represented in the period 15 / 19 repeats. Anyway, just thinking of a model that will replicate what we are observing.
I also wondered about the strong representation of the "+" symbol in the bigram repeats. First of all, if you expand (make all instances unique) of the symbols that occur 10 or more times, bigram repeats will still peak at period 15 /19. Secondly, I was able to recreate the number of bigram repeats occupied by such a high frequency symbol in test ciphers IF it was a 1:1 substitute. Looking at p1 of my plaintext library the most frequently occuring bigrams are "il" and "th" with a count of 11 both. It are exactly bigrams like these which have the highest chance of surviving the homophonic substitution process. Randomly distributing 24 nulls throughout a message will generally not induce such high counts.
I don’t know if this type of measurement would be useful, but if you have 1 2 3 4 3 2 1 2 3 4 3 2 1, the 2’s would be closer together and then farther apart. And the 3’s would be closer together and then farther apart. Maybe for each symbol, find the positions and the distances between each, alternating distances. If the odd distances are generally smaller than the even distances, or vice versa, generally for some symbols, then maybe the measurements all added up would be different than for perfect regular cycles. Jarlve, you probably already thought of something like that.
Not really, I’ll get on it.