smokie, we can skip to 8 nulls & skips as you suggested. I tested that using a higher amount of nulls & skips than the cipher has will still result in a solve.

New AZdecrypt update: https://drive.google.com/open?id=1ewupo … xWr87HPBfm

Added multiplicity to the output window and solve log. Added 2 settings, "manual nulls" and "manual skips", putting any value other than 0 in either one will cause the solver to override the "nulls & skips" settings. Say that a cipher has 3 nulls and 4 skips than you can use "manual nulls: 3" and "manual skips: 4" to solve it specifically. We need these settings for testing.

The manual nulls and skips settings sound great for finding optimum iterations.

I found a utility that merges text files, and can now merge all of the output files for all divisions into one big text file, then paste it into a spreadsheet and use text formulas to extract score, null and skip positions. Noticing that for the smokie_17/0, about half of the positions were perfect or very close, I decided to look into that some more. Perhaps take all of the highest scoring messages from each of multiple restarts, and those positions are most likely to be correct. So I can look at that information now all together. I already did it once, but now have to make a spreadsheet that automatically does it.

I found a utility that merges text files, and can now merge all of the output files for all divisions into one big text file, then paste it into a spreadsheet and use text formulas to extract score, null and skip positions. Noticing that for the smokie_17/0, about half of the positions were perfect or very close, I decided to look into that some more. Perhaps take all of the highest scoring messages from each of multiple restarts, and those positions are most likely to be correct. So I can look at that information now all together. I already did it once, but now have to make a spreadsheet that automatically does it.

That is cool. Let me know how it works out. And if I could automate something.

Let me ask a question. The null skip detection hill climber makes small, random changes to a group of null and skip positions, and then the substitution hill climber works on that for a while to determine if the random change in the null and skip position needs to be kept or not kept, right? Is that how it works? So, the program is getting really good partial solutions but the null or skip positions are off just by a few positions a lot of the times. Setting aside the recent conversation about fine tuning, would the program be more efficient at finding these near perfect positions if it make the small random changes to the null and skip positions by choosing from only say, odd or even positions?

No it does not matter. In period 20 we have 20 columns. If then a random number between 1 and 340 is chosen it has a 5% chance to fall into any one column. Since any one column in period 20 takes up 17 positions. Change that to a random number between 1 and 340 using only even numbers gives the possibilities 2, 4, 6, 8, 10, etc… and the same 5% chance to fall into any one column because the positions of the period 20 column have also halved.

I thought of this again and had to search back to find the conversation, which gives me another idea and forgive if this upsets the current approach to finding the positions of a lot of nulls and skips.

1. Start with a horizontal array of 340 cells, filled with numbers, not symbols, 1 18 35 52 69 86 103 120 137 154 171 188 205 222 239 256 273 290 307 324 2 19 36 53, etc. Basically a P20 matrix;

2. Insert nulls and skip numbers to simulate the proposed issue with the 340;

3. Randomly choose locations for nulls and skips, trying to figure out where they really are, and make a second array of 340 cells with the adjustments;

4. Pour the array into a 17 x 20 grid of cells TBLR ( so far nothing different than the program does now );

5. Make another 17 x 20 grid, empty;

6. In the empty grid, start with column 1, row 1. Make this cell true if the value in poured grid column 2, row 1 is the value of poured grid column 1, row 1 + 1. Do this for every empty grid cell. A score of 340 trues is perfect, and mis-alignments reduce the score;

7. Experiment with and fine tune algorithm using this method instead of with actual encoded message to find most efficient approach, then apply to encoded messages.

Basically I am saying, hill climb the matrix instead of a message to help us understand how to further fine tune the hill climbing operation, and perhaps to get a better idea of how many iterations it would take to get a perfectly untransposed matrix / message depending on how many nulls and skips there are.

Your +1 idea is a good one and it is something that I have used previously to determine the goodness of approximating one transposition with another. It simulates a perfect measurement at lightning speed. Downscale the problem and work your way up. A middle ground would be to use plaintext ciphers with 100000 substitution iterations and 5-grams or lower. I tried this and a period 20 plaintext cipher with 5 nulls & 5 skips which solved almost instantly. So apparently it is the diffusion from the homophonic substitution (higher multiplicity) which makes this problem so hard.

I will test the following, for smokie_p20_5nulls_5skips, with 5 nulls & 5 skips manually set:

1. get solve% for 80k hc iterations and 500k sub iterations
2. get solve% for 40k hc iterations and 1000k sub iterations
3. get solve% for 20k hc iterations and 2000k sub iterations
4. get solve% for 10k hc iterations and 4000k sub iterations

The idea is that on harder problems, where the solver has a very hard time catching on, more substitution iterations may be more beneficial. I am not very sure but it needs to be tested.

Three ways to work on the null skip hillclimber. Matrix, 1:1 substitutes, and homophonic. A person would think that the same matrix or message, with nulls and skips in the same locations, should require the same number of iterations to get a solution, regardless of matrix, 1:1 or homophonic.

But, could misalignments in a 1:1 or homophonic cause false high scoring n-grams to occur, thus holding in place a chosen null or skip location for a lot of future iterations? And is there a difference between 1:1 and homophonic, and if so, why?

EDIT: Is this why using 6 grams works better than 5 grams?

But, could misalignments in a 1:1 or homophonic cause false high scoring n-grams to occur, thus holding in place a chosen null or skip location for a lot of future iterations? And is there a difference between 1:1 and homophonic, and if so, why?

It is about the solver’s diminished ability to tell good from bad. It is not so much that it is holding a chosen null or skip in place for a lot of future iterations. Though, if that is suspected the temperature setting will offer a way out. The temperature controls the ratio between hill climbing and random walking, such that a lower temperature will increase hill climbing and a higher temperature will increase random walking.

You can do a very simple test to see how well a solver can distinguish between good or bad:

Using 5-grams, take the p1 plaintext and get its score, it is 24865. Now, randomize it a few times and get the average randomized score, it is about 15000. That is a 65% increase going from 15000 to 24865. Do the same for a 63 symbol p1 cipher and now there is only a 24% increase.

Using 6-grams, the p1 plaintext shows a 112% increase and the 63 symbol p1 shows a 50% increase.

Certainly, with transposition, these percentage increases are not to be trusted blindly as interruptions have a stronger effect on longer ngrams. Another problem with 6-grams versus 5-grams is that using 6-grams is about 2.6 times slower. Within the same time frame, on the cipher jarlve_p20_5nulls_3skips, using 5-grams is slightly superior to using 6-grams. It is possible that on increasingly harder nulls & skips ciphers 6-grams may overtake 5-grams within the same time frame. I will test it on smokie_p20_5nulls_5skips.

Solve% for smokie_p20_5nulls_5skips appears to be between 1% and 2% with 80k hc while removing the 5 relocated skips at the end. It is gonna take time to figure it out but I do not mind.

EDIT: this 1% to 2% is for the cipher at the correct nulls & skips division.

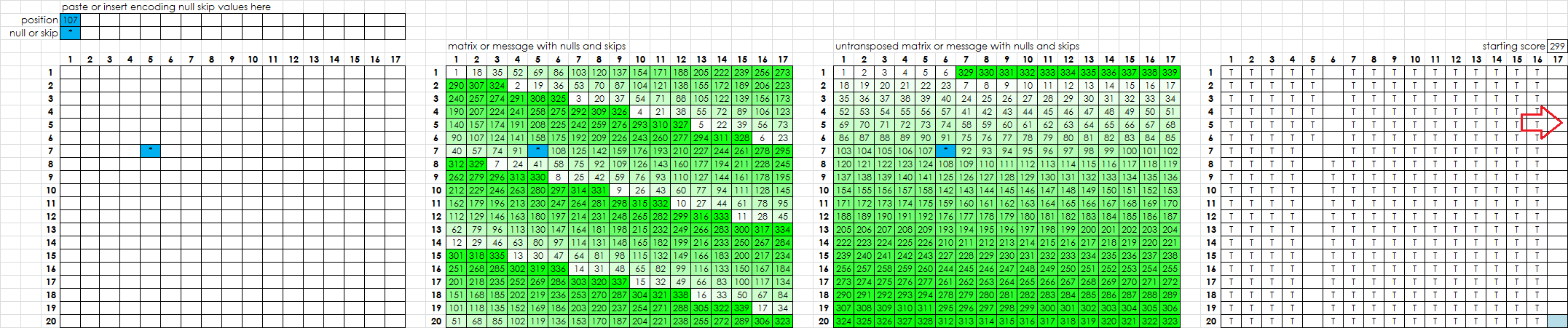
I may have an explanation for why the correct null skip division scores higher than a low null high skip division. See below the matrix, with one null inserted at position 107. This actually creates two misalignments, one at the null, and one at the far right untransposed column. Scroll far right to see big red arrow.

I also did this with text to verify that I wasn’t making a mistake. A null shifts everything poured after it into the untransposed grid and therefore the text will not read from one row down to the next lower row. Instead it reads into the same row.

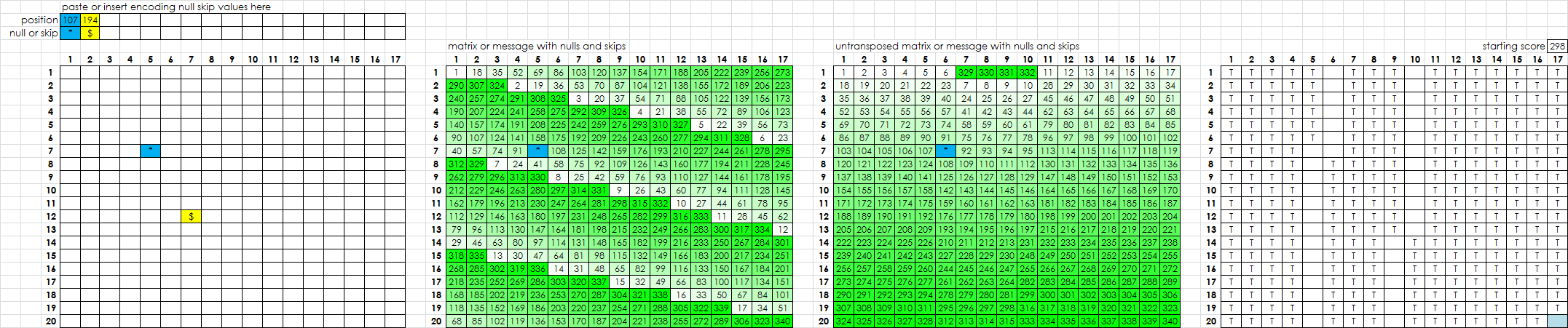
Now if I am looking for one null, and decided to delete the symbol at random position 194, I create a new misalignment at the deletion, but that corrects the misalignment in the far right column. Scroll far right.

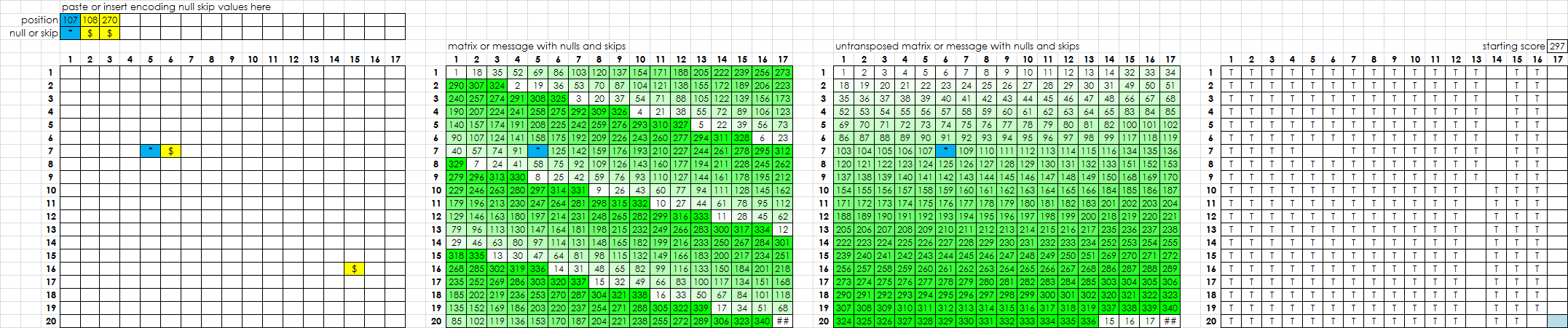
Same thing happens for two nulls, or any division. If I delete the same number of symbols as there really are nulls, and add the same number of wildcards as there really are skips, as long as these occur in columns 1-16 and not column 17, the misalignment between column 17 and column will be corrected for. The message will score higher than a low null high skip division, but maybe just a little bit more, giving it the winning edge.

Of course there are still two misalignments now, but if I accurately detect and delete the null at position 107 this will be corrected for. If I were working with a division that had even one more null or skip, there would be two more misalignments created, one of them between column 17 and column 1.

I may have an explanation for why the correct null skip division scores higher than a low null high skip division.

It only seems logical that it does. Just on average, the correct division should (theoretically) score higher.

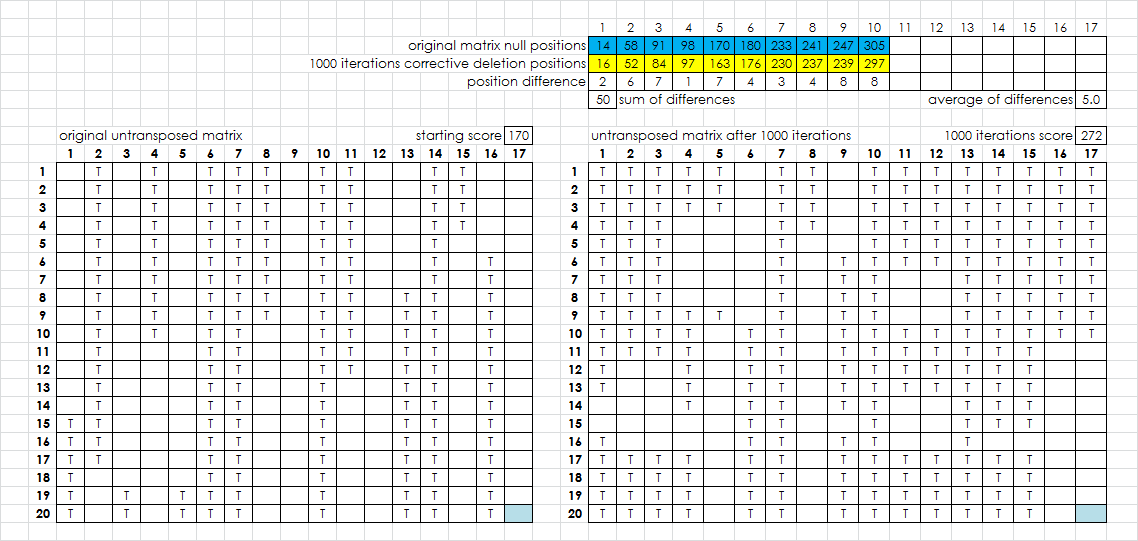
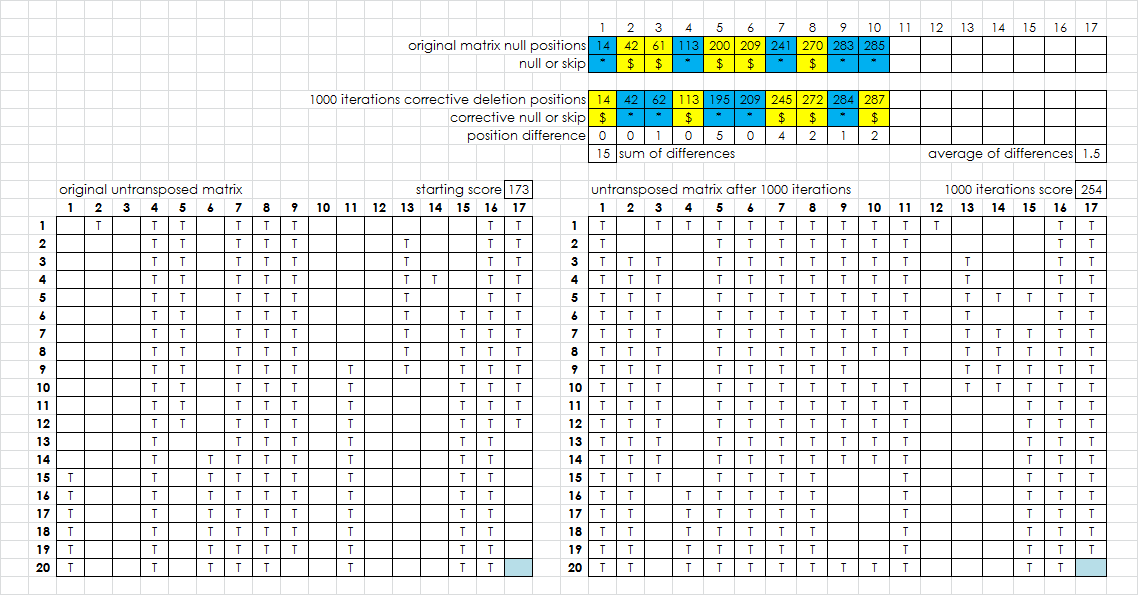
I have my matrix +1 hill climber almost done. It is on the old laptop, a pea shooter, so I only use 1,000 iterations ( rows on the spreadsheet ). But, with 10 nulls, the hill climber consistently gets close to the correct positions with only 1,000 iterations. There are so far no rules for funneling or fine tuning the close positions to the correct positions yet, but that is what I will be working on later today.

Cool!

Now showing mix of 5 nulls and 5 skips. The sheet still works great with only 1,000 iterations, but need some fine tuning because at the top it doesn’t always line up the corresponding positions.