O.k. now I have a spreadsheet so that all I have to do is paste the 10,000 ( or slightly fewer ) iterations from the text file, and it will break it into fields, then show all of the rows with acceptances in a separate section, all together, and show all of the rows where the program started with a new key in a separate section, all together.

What is that called? It is like a restart within a restart, except that it remembers the ones before it that the program was successfully able to get a solution from? The new key starts at intervals, 620 iterations four times in a row, then 828 iterations two times in a row. What is that and how do you calculate it? Thanks ( this is awesome ).

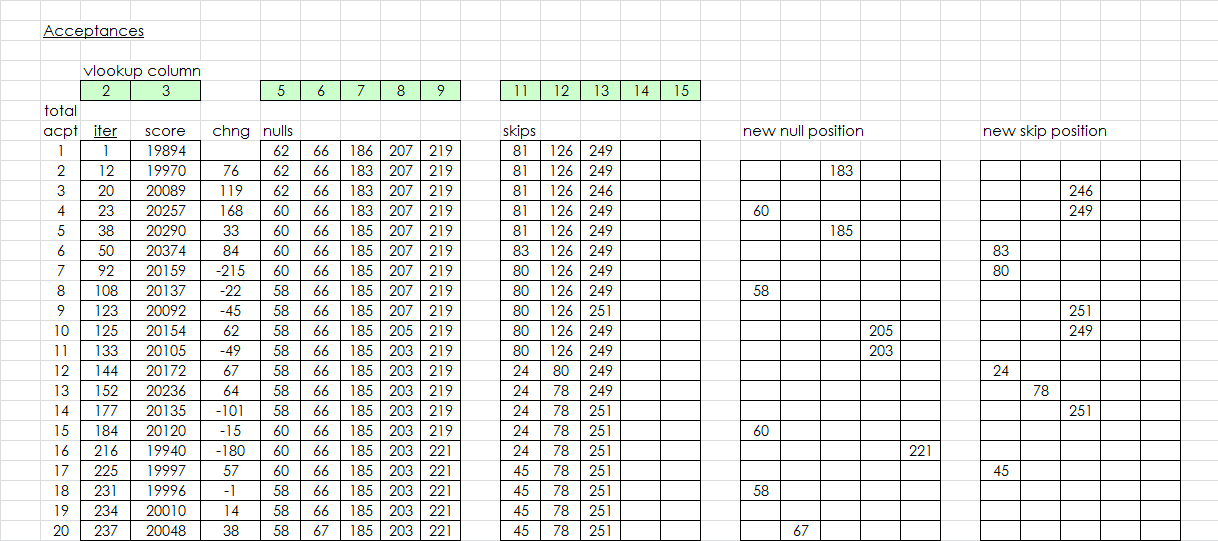
A screenshot of the acceptances:

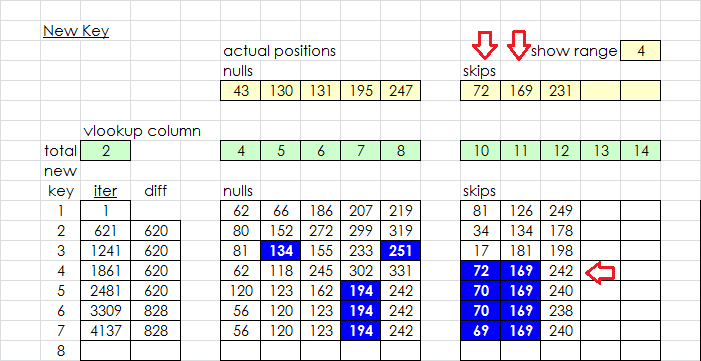
And a screenshot of the new keys. I can input a range, and it will highlight blue the positions that correctly fall within the range of the actual positions. I am trying to figure out why sometimes the program finds a solution, and why most of the time it doesn’t. Below on the third key, there were two positions that were within four positions of actual, but that didn’t seem to work. So, the program generated the fourth key, where two positions were exactly dead on actual positions. That did the trick, and a solution quickly followed. This was Jarlve 5/3 with Shift 50 Shift Divisor 7 10000 iterations 100 restarts. It was the only solution, but I am looking at extremes to figure out what the program is doing. It is very interesting.

EDIT: After the program randomly selected the two exact positions out of 8, the score dropped 743 points, but it only took 1270 more iterations to find a solution.

What is that called? It is like a restart within a restart, except that it remembers the ones before it that the program was successfully able to get a solution from? The new key starts at intervals, 620 iterations four times in a row, then 828 iterations two times in a row. What is that and how do you calculate it? Thanks ( this is awesome ).

It is my sub restart system: https://drive.google.com/open?id=0B5r0r … kg4VFFuMms

I have it set at 4 levels at the moment. It should be 4 times 625 iterations, 3 times 833 iterations, 2 times 1250 iterations and 1 time 2500 iterations. It may lose a few iterations here and there because of a small bug with how it counts.

O.k., thanks a lot for answering my questions. I appreciate it.

Your screenshots look cool smokie. You are very good at this.

I am trying to figure out why sometimes the program finds a solution, and why most of the time it doesn’t.

I am pretty sure that a big part of the problem is not about the algorithm, that said, the algorithm could still be improved of course. With harder ciphers, the substitution solver becomes less and less effective at judging good from bad.

O.k., thanks a lot for answering my questions. I appreciate it.

I was waiting for you to find about it and you did (sub restarts). That is commendable!

Maybe, but… the substitution solver works really, really well. Enough of the corrective skips and nulls have to simultaneously wander close enough to the actual null skip positions that there are few misalignments and the substitution solver can do the rest. The question is, how many and how close is close enough.

I am concerned that a P15 message will be much more difficult to solve that a P20. I am guessing only at this point, but for P20, I think that a corrective skip or null would have to wander within 10 positions of the actual null or skip position for the substitution solver to be able to detect anything. The corrective skip or null will cause a misalignment itself, and would have to correct more that it mis-aligns. In other words, close enough so that it does more good than bad. With P15, it may be only 7 positions or closer. P19 may be slightly more difficult to solve than P20.

Mis-alignments are going to cause a lot of n-grams that are not frequently used, and fewer frequently used n-grams. I don’t think that the orbiting is a big part of the problem. It is a very small part only. I will continue to examine the iterations and experiment with different solver options mostly with 10,000 iteration experiments for now.

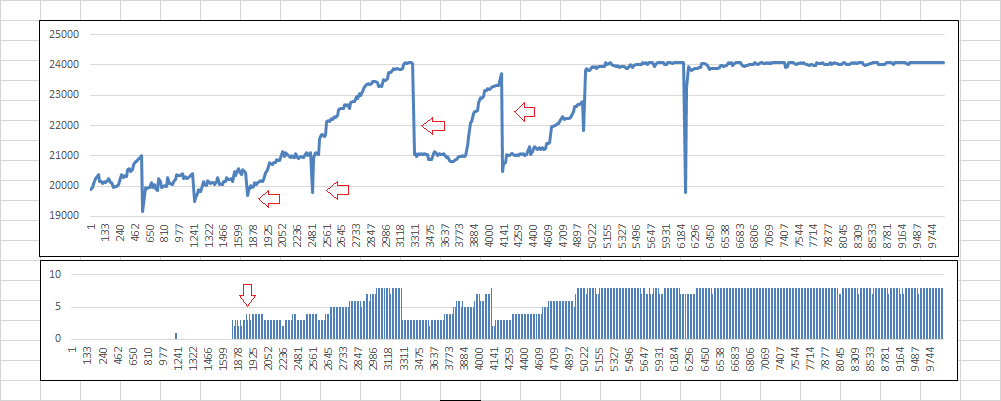
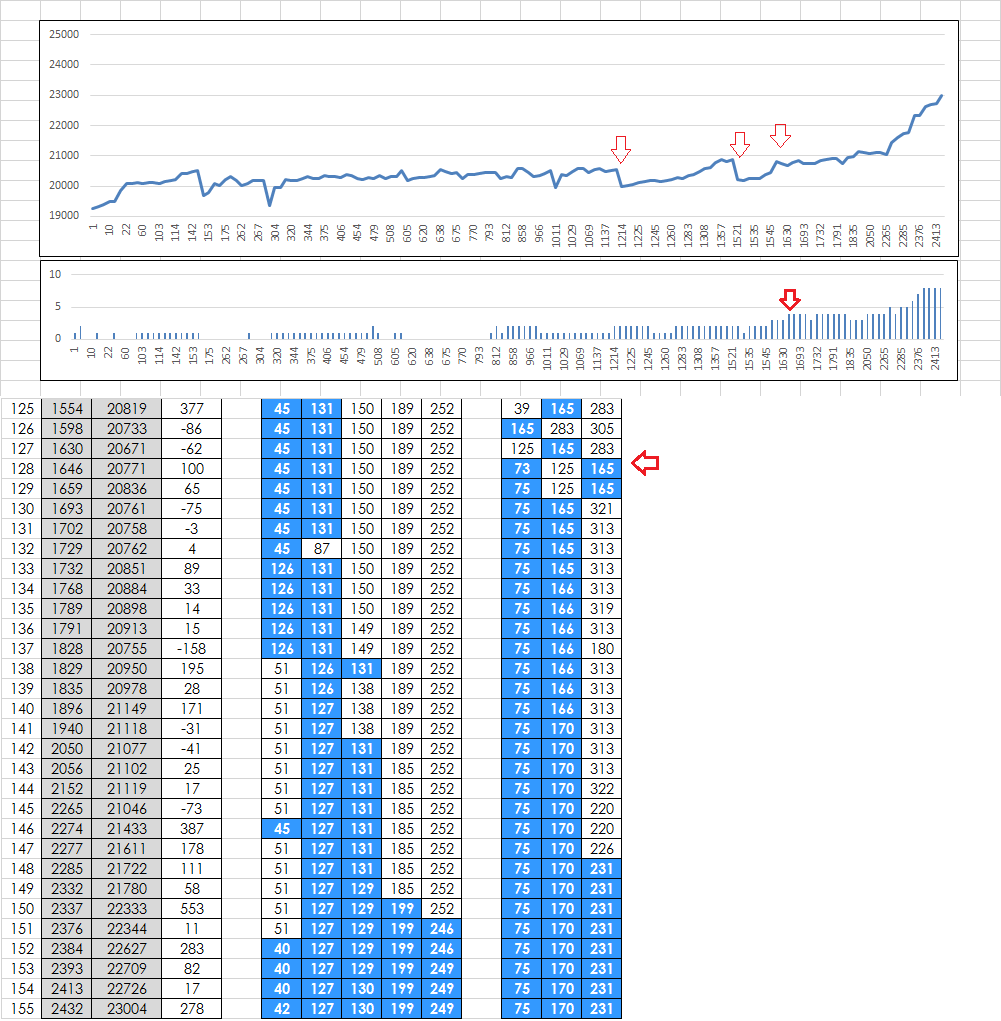
The spreadsheet is getting bigger and more elaborate. I can now designate a position range for orbiting, and the symbols will highlight a pinkish color when orbiting within that range. I can also show for every acceptance, highlighted in blue if within a range that I specify from actual position ( not shown ). And a graph, above, the score of each acceptance, with iteration number on x axis. The drops indicate sub restarts. On bottom, the number of symbols within the position range, which I have set to 2 positions of actual for the graph. The faint, red, downward pointing arrow showing that three symbols are within 2 positions of actual, which is where the climbing got going.

Maybe, but… the substitution solver works really, really well. Enough of the corrective skips and nulls have to simultaneously wander close enough to the actual null skip positions that there are few misalignments and the substitution solver can do the rest. The question is, how many and how close is close enough.

I am doing a comparison on smokie 5/5.

500k substitution iterations @ 80k hc iterations versus
1000k substitution iterations @ 40k hc iterations versus
2000k substitution iterations @ 20k hc iterations

The idea is to trade hc iterations for substitution iterations. The first test had a 1.3% solve%, the second test 1.9% and the third test has just started. It takes 5 days per test. Since the second test is almost 50% better than the first test it looks that on smokie 5/5, we are not giving the substitution solver enough time. The extra substitution iterations are helping to judge good from bad. Good news.

I am concerned that a P15 message will be much more difficult to solve that a P20. I am guessing only at this point, but for P20, I think that a corrective skip or null would have to wander within 10 positions of the actual null or skip position for the substitution solver to be able to detect anything. The corrective skip or null will cause a misalignment itself, and would have to correct more that it mis-aligns. In other words, close enough so that it does more good than bad. With P15, it may be only 7 positions or closer. P19 may be slightly more difficult to solve than P20.

I think it should be easier because the search space is smaller.

Mis-alignments are going to cause a lot of n-grams that are not frequently used, and fewer frequently used n-grams. I don’t think that the orbiting is a big part of the problem. It is a very small part only. I will continue to examine the iterations and experiment with different solver options mostly with 10,000 iteration experiments for now.

I would like to see a before and after test with the fix of not allowing a null and a skip in the same place. At least with 500 restarts and initially not with smokie 5/5. Is that something you would like to do smokie?

The spreadsheet is getting bigger and more elaborate. I can now designate a position range for orbiting, and the symbols will highlight a pinkish color when orbiting within that range. I can also show for every acceptance, highlighted in blue if within a range that I specify from actual position ( not shown ). And a graph, above, the score of each acceptance, with iteration number on x axis. The drops indicate sub restarts. On bottom, the number of symbols within the position range, which I have set to 2 positions of actual for the graph. The faint, red, downward pointing arrow showing that three symbols are within 2 positions of actual, which is where the climbing got going.

That score versus iterations graph is amazing! It is very helpful to me.

I would like to see a before and after test with the fix of not allowing a null and a skip in the same place. At least with 500 restarts and initially not with smokie 5/5. Is that something you would like to do smokie?

We could put that on a to-do list. I am not overly concerned about it. I have been looking and will continue to examine orbiting, which looks like this on the spreadsheet now. I noticed also that sometimes you can have two nulls with the same position, or even two nulls and one skip with the same position. A null and a skip will cancel each other out, but if there are two nulls or two skips on the same position, then there will be an additional misalignment and the solver will treat it like it is the wrong division. However, the computer can break away from orbiting. I doubt that, even if you fix it, it will cause a substantial increase in solve rates. It only takes up maybe 10% of the iterations, at most. If you want to do the fix, that is fine, or perhaps keep a punch list and do it with other stuff at the same time. Not sure it is worthy of a new version just yet. If you want I can always test something.

Forgive me if I am going in a different direction right now. I am not concerned about the 340 currently, only want to learn about hill climbing and the program. I am not at all ready for the 340. I am trying to figure out how to get the most number of solves in 1 million iterations. I have to look at a lot more, but from the few solves that I have looked very closely at, the program will do a sub restart, one with a lot of new symbols as compared to the prior acceptance, the score will drop, but then the hill climbing really takes off. Not so much when there is a sub restart and the symbols are mostly the same as the prior acceptance.

I think that there is an optimum spacing between sub restarts depending on the number of nulls and skips, and finding that sweet spot is good plus I still have a pea shooter and need to find ways to maximize what I have.

Check out this one. 2,500 iterations total. The two arrows on the left are a couple of sub restarts, but not all are marked. They are the little drops. The arrow on the right is at iteration 1,646, where the program finds four null / skip within 4 positions of actual. Then, it takes off and up and up very quickly. The bottom chart is number of symbols within 4 positions of actual.

I have to experiment with other things so that I understand how the program works so will keep you posted. I have to see for myself sometimes.

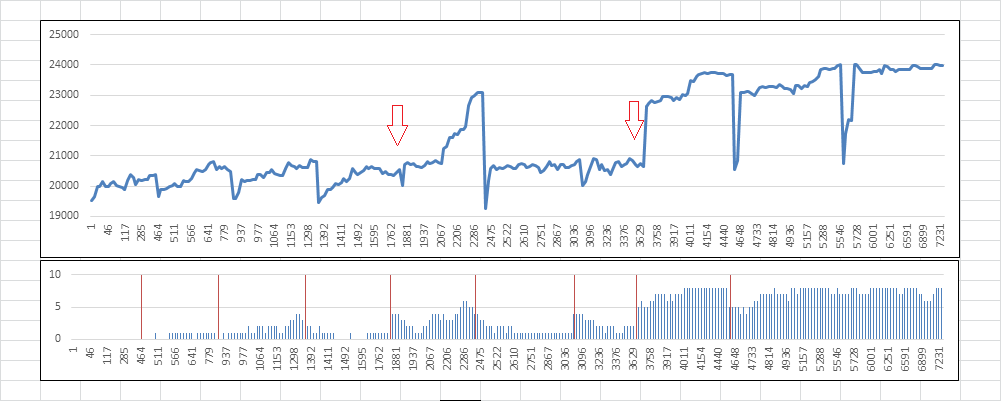
Here is one, 7500 iterations Jarlve 5/3 shift 15% shift divisor 2. I added little vertical red lines at the sub restarts. They don’t line up exactly with the graph above because of Excel, but they do line up. Sub restart intervals at 463, 463, 463, 463, 620, 620, 620, 932.

At restart 1853 4th sub restart, there were 6 new positions as compared to the prior acceptance, 4 positions then were within 2 positions of actual. There was a partial solve in only 620 more iterations.

At restart 3713 7th sub restart, there were 7 new positions as compared to the prior acceptance, 5 positions then were within 2 positions of actual. There was a solve in about 1000 more iterations.

The x axis is out of scale, showing only acceptances.

EDIT: There were only 195 iterations out of 7,500 where there was orbiting, which is only about 2.6% of iterations. Much less than the 10% that I said above, partly because it is a 5/3. Hopefully that will make you feel less concerned about it.

We could put that on a to-do list. I am not overly concerned about it. I have been looking and will continue to examine orbiting, which looks like this on the spreadsheet now. I noticed also that sometimes you can have two nulls with the same position, or even two nulls and one skip with the same position. A null and a skip will cancel each other out, but if there are two nulls or two skips on the same position, then there will be an additional misalignment and the solver will treat it like it is the wrong division. However, the computer can break away from orbiting. I doubt that, even if you fix it, it will cause a substantial increase in solve rates. It only takes up maybe 10% of the iterations, at most. If you want to do the fix, that is fine, or perhaps keep a punch list and do it with other stuff at the same time. Not sure it is worthy of a new version just yet. If you want I can always test something.

Okay, sure. I will see about running that test myself. Two or more skips on the same position should be allowed, but not two or more nulls. I will fix these small issues with the next update. Thank you for pitching in!

Forgive me if I am going in a different direction right now. I am not concerned about the 340 currently, only want to learn about hill climbing and the program. I am not at all ready for the 340. I am trying to figure out how to get the most number of solves in 1 million iterations. I have to look at a lot more, but from the few solves that I have looked very closely at, the program will do a sub restart, one with a lot of new symbols as compared to the prior acceptance, the score will drop, but then the hill climbing really takes off. Not so much when there is a sub restart and the symbols are mostly the same as the prior acceptance.

That is no problem. A slowdown is good. What do you mean with 1 million iterations? A total number of 1 million hc iterations? Something like 20 x 50k versus 40 x 25k etc.

Check out this one. 2,500 iterations total. The two arrows on the left are a couple of sub restarts, but not all are marked. They are the little drops. The arrow on the right is at iteration 1,646, where the program finds four null / skip within 4 positions of actual. Then, it takes off and up and up very quickly. The bottom chart is number of symbols within 4 positions of actual.

Thank you for these graphs, again, it is really interesting to see it that way. The taking off is when it finds the hill of the global maximum.

EDIT: There were only 195 iterations out of 7,500 where there was orbiting, which is only about 2.6% of iterations. Much less than the 10% that I said above, partly because it is a 5/3. Hopefully that will make you feel less concerned about it.

Not concerned at all, just want to find out the truth.

What do you mean with 1 million iterations? A total number of 1 million hc iterations? Something like 20 x 50k versus 40 x 25k etc.

Yes, 1 million hc iterations. I am working a lot of short tests that I can get results from and move on to the next test so that I can figure out what the program is doing without having to wait several days. It is really a lot of fun, and I like the 3D picture.