I’m currently working on a new idea and collecting data from various tests. The whole thing is a bit more time-consuming, but I hope to finish it this weekend. Until then, I have a mystery cipher here. I don’t think it can be solved automatically with the current tools. But I don’t want to bet on that.
;b33h4xnF7q19chd9 =740PqKNFAexNXTyF ;vA9TLCGr0NM;Q+ml FGF3R:njJ0i+45d-Y TAV4yXCLQKmSRoBtV dYti+5LHl=qrXbuM1 X+BSMRIC0pKabveBw =9oj+JLhiTNir0U-x GPSE7sdeQ0bYZc4in 0m5oJeAXK;t+KuV3: 4RF7LPqTUMlT=v91r ejbF+XmcG5bhNnC-J 0TYHoQd+;S9tTyYV= Tuy0=APN+XlxDR:1J rL+Nni49swM-+UKi+ ;sOwdD+h7HVG0Yqi0 CeR:THZcvbjtYXRK3 4yF=5E+0TAI0xwOc9 0XeqlubvRQ1oMxYBS hOim+jP=-3=7RMFTU
Translated with http://www.DeepL.com/Translator
IACCESSWHICHISWHYTHI SWASPOSTEDONAMONDAYI NSTEADOFOVERTHEWEEKE NDANDTHISYEARINSTEAD OFTALKINGABOUTANOTHE ROFMYFAVORITEFICTION ALSUPERHEROESASIVEDO NEINYEARSPASTIVEDECI DEDTOWRITETHEINSANEL YOVERTHETOPSTORYOFAR EALLIFEMANOFSTEELSOF ALLSHATTERINGLYRIDIC ULOUSYOUDTHINKTHEENT IRESTORYWASTHEPRODUC
As almost always you have found the solution impressively fast. And as always, I forgot that we had discussed a similar idea before. I remember a kind of heat map that could be used to visualize interrupted cycles. Unfortunately I can’t find this option in AZDecrypt anymore. Did you solve it this way?
However, a piece of the solution is missing (it is 53.txt from your Plaintext library). The cipher was created as follows:
The plaintext was substituted with the following key:
KMLdDphcC5mnGVto1l-iZax3y94bekBHwsNrvSQ+0Pgj:uU;Aq7RX=YOIEJF2TW AAAABBCCDDDEEEEEEEEFGGHHHIIIIJKLLLMNNNNOOPQRRRRSSSSTTTTUUUVWXYZ
It was then transposed in the following way:
Column 13 from top to bottom
Column 8 from top to bottom
Column 3 from top to bottom
Then all columns from right to left.
The matching matrix:
74 73 41 72 71 70 69 21 68 67 66 65 1 64 63 62 61 88 87 42 86 85 84 83 22 82 81 80 79 2 78 77 76 75 102 101 43 100 99 98 97 23 96 95 94 93 3 92 91 90 89 116 115 44 114 113 112 111 24 110 109 108 107 4 106 105 104 103 130 129 45 128 127 126 125 25 124 123 122 121 5 120 119 118 117 144 143 46 142 141 140 139 26 138 137 136 135 6 134 133 132 131 158 157 47 156 155 154 153 27 152 151 150 149 7 148 147 146 145 172 171 48 170 169 168 167 28 166 165 164 163 8 162 161 160 159 186 185 49 184 183 182 181 29 180 179 178 177 9 176 175 174 173 200 199 50 198 197 196 195 30 194 193 192 191 10 190 189 188 187 214 213 51 212 211 210 209 31 208 207 206 205 11 204 203 202 201 228 227 52 226 225 224 223 32 222 221 220 219 12 218 217 216 215 242 241 53 240 239 238 237 33 236 235 234 233 13 232 231 230 229 256 255 54 254 253 252 251 34 250 249 248 247 14 246 245 244 243 270 269 55 268 267 266 265 35 264 263 262 261 15 260 259 258 257 284 283 56 282 281 280 279 36 278 277 276 275 16 274 273 272 271 298 297 57 296 295 294 293 37 292 291 290 289 17 288 287 286 285 312 311 58 310 309 308 307 38 306 305 304 303 18 302 301 300 299 326 325 59 324 323 322 321 39 320 319 318 317 19 316 315 314 313 340 339 60 338 337 336 335 40 334 333 332 331 20 330 329 328 327
It is therefore a transposition AFTER the substitution. The cipher thus retains a certain cyclic behavior. Depending on the direction in which the rows and columns are written, this could result in pivots. Detailed tests are still to be done.
I automatically created several thousand test scripts with this matrix and noticed that many of them had a bigram peak at P17 or P18. I will deliver numbers and tables later, that’s not finished yet.
So I’m trying to figure out if such a crossed matrix could be a possible option for z340. However, the fact that my cipher was solved so quickly is a good argument against my idea. And as mentioned at the beginning: I think I had posted something similar before. In this case it would be almost embarrassing for me to have forgotten ![]()
Translated with http://www.DeepL.com/Translator
I remember a kind of heat map that could be used to visualize interrupted cycles. Unfortunately I can’t find this option in AZDecrypt anymore. Did you solve it this way?
Yes, I used that test, renamed to "Find sequential homophonic randomizations". I changed so much with 1.14 and forgot to mention it. The cipher also has better cycle stats after mirroring/flipping it.
It is therefore a transposition AFTER the substitution. The cipher thus retains a certain cyclic behavior. Depending on the direction in which the rows and columns are written, this could result in pivots. Detailed tests are still to be done.
Okay, interesting. Will wait for your analysis.
Postby doranchak » Sat Apr 08, 2017 6:00 am
Interesting observations, smokie. The herringbone pattern reminds me of interference patterns, such as https://en.wikipedia.org/wiki/Moir%C3%A9_pattern
I wonder if we can determine whether this arises naturally or as a consequence of a transposition scheme.
http://www.zodiackillersite.com/viewtop … one#p52521
I don’t know, but it has been two years and I am still wondering about this. See below left, the pivots, and all cells highlighted for P16, P32 and P48 unigram repeats, totaling 48 cells. On the right, the herringbone pattern of P16 RLBT repeats that have the same symbols as P19. I keep wondering if this is some type of transparency.
So, to clear things up, these are the equally spaced diagonal P16 rows that make up the pattern, without the other rows. I counted 109 cells highlighted above with all P16 RLBT, and 57 cells with these rows only.
I guess that I should point out that they contribute to the pivots for 4 cells.
Two years ago I tried to use complex route transposition this matrix, to make the herringbone pattern, and I was successful with practice messages to do that, but could not generate P19 stats because only two thirds of the plaintext was transposed to make P19, and one third was transposed to make P16 RLBT. Those equally spaced rows in the post above are two thirds of the message. Actually, this matrix is a little bit more than two thirds to make P19. I highlighted a few positions so you can see the pattern.
311 002 199 330 177 155 328 133 111 325 089 067 321 045 023 316 001
047 025 306 003 200 329 178 156 326 134 112 322 090 068 317 046 024
070 307 048 026 301 004 201 327 179 157 323 135 113 318 091 069 312
308 093 071 302 049 027 296 005 202 324 180 158 319 136 114 313 092
138 116 303 094 072 297 050 028 291 006 203 320 181 159 314 137 115
161 304 139 117 298 095 073 292 051 029 286 007 204 315 182 160 309
305 184 162 299 140 118 293 096 074 287 052 030 281 008 205 310 183
010 207 300 185 163 294 141 119 288 097 075 282 053 031 276 009 206
033 266 011 208 295 186 164 289 142 120 283 098 076 277 054 032 271
267 056 034 261 012 209 290 187 165 284 143 121 278 099 077 272 055
101 079 262 057 035 256 013 210 285 188 166 279 144 122 273 100 078
124 263 102 080 257 058 036 251 014 211 280 189 167 274 145 123 268
264 147 125 258 103 081 252 059 037 246 015 212 275 190 168 269 146
192 170 259 148 126 253 104 082 247 060 038 241 016 213 270 191 169
215 260 193 171 254 149 127 248 105 083 242 061 039 236 017 214 265
227 019 216 255 194 172 249 150 128 243 106 084 237 062 040 231 018
064 042 224 020 217 250 195 173 244 151 129 238 107 085 232 063 041
087 225 065 043 222 021 218 245 196 174 239 152 130 233 108 086 228
226 110 088 223 066 044 221 022 219 240 197 175 234 153 131 229 109
340 339 338 337 336 335 334 333 332 331 220 235 198 176 230 154 132
So that was a flop, but I still wanted to work on this some more in another way recently.
I randomly selected 109 positions 1000 times, and the test was to find out if positions on those rows were selected, but also with a position next to it selected. Here is a good one, with 39 positions, but definitely not 57.
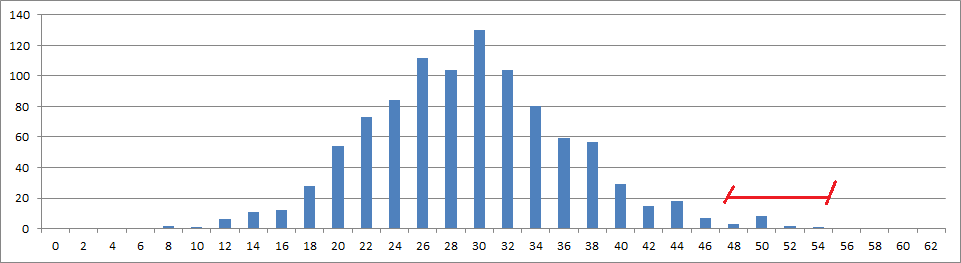
I did it over and over again, but here is a typical column chart. X axis is count of cells, and Y axis is the number of times that happened. Nothing close to 57 cells.
But if I randomly select 170 cells, or half the message, then I can get a few that are close to 57 cells. Here is the best out of 1000, and it is 56 cells.
Here is the graph. You can see that even if I select 170 positions 1000 times, only one comes close.
I don’t know if this is a good way to test whether the P16 RLBT bigram repeats on those evenly spaced rows that make the herringbone pattern.
I tried to solve it by making it into fragments and using the rows bound solver.
Here are the schemes, schemes 1-3 are P19, and scheme 4 is the P16 RLBT.
scheme 1
1 19 37 44 11 56 8 60 31
4
55 3 3 19 53 4 32 11 5
11 25
21 37 8 2 50 51 8 50 16
3 33 26 10
22 16 61 7 25 53 36 48 19
11 14 56 43 40
46 3 57 22 16 5 61 52 3
6 59 40 63 9 27 62
42 37 51 58 19 20 29 37 51
40 51 30 31 29 42 20 31
18 35 7 49 30 59 40 63 55
38 36 34 50 56 7 26 21 36
scheme 2
40 54 41 18 61 8 37 33
51 1
29 38 48 30 50 36 39 15
19 17 5
50 41 19 41 27 37 21 19
36 19 40 48 39
44 31 49 3 23 5 19 44
20 45 12 36 46 44
5 19 6 16 46 36 51 31
63 18 35 21 19 1 30 58
34 43 48 55 36 27 62 34
29 42 32 47 5 6 54 56
scheme 3
2 20 19 30 50 10 28 13
4 22 39 45 9 4 13
5 23 15 5 19 16 11
7 25 21 19 53 21
8 26 33 19 10
10 28 22 31
11 29 40 16
13 31 41
14 32
16
17
scheme 4
11 55 33 13
19 36 28 12 7 22 11 11 19 51 18 15 51 52 3 1 33
20 5 3
19
37 10 26 13 20 53 16 11 14 20 43 34 19 40 25 54
5 47 5 36 21 6
18 29 26 56 23 2 28 20 28 14 20 53 47
17 15 19 7 40 6 38 24 9
42 20 23 51 28 38 53 58 20 23
16 19 6 19 32 24 23 17 8 26 27 12
23 23 14 20 57 55 19
34 15 47 6 50 19 39 23 38 17 51 23 13 30 15
Here is the whole thing, all combined.
1 19 37 44 11 56 8 60 31 4 55 3 3 19 53 4 32 11 5 11 25 21 37 8 2 50 51 8 50 16 3 33 26 10 22 16 61 7 25 53 36 48 19 11 14 56 43 40 46 3 57 22 16 5 61 52 3 6 59 40 63 9 27 62 42 37 51 58 19 20 29 37 51 40 51 30 31 29 42 20 31 18 35 7 49 30 59 40 63 55 38 36 34 50 56 7 26 21 36 40 54 41 18 61 8 37 33 51 1 29 38 48 30 50 36 39 15 19 17 5 50 41 19 41 27 37 21 19 36 19 40 48 39 44 31 49 3 23 5 19 44 20 45 12 36 46 44 5 19 6 16 46 36 51 31 63 18 35 21 19 1 30 58 34 43 48 55 36 27 62 34 29 42 32 47 5 6 54 56 2 20 19 30 50 10 28 13 4 22 39 45 9 4 13 5 23 15 5 19 16 11 7 25 21 19 53 21 8 26 33 19 10 10 28 22 31 11 29 40 16 13 31 41 14 32 16 17 11 55 33 13 19 36 28 12 7 22 11 11 19 51 18 15 51 52 3 1 33 20 5 3 19 37 10 26 13 20 53 16 11 14 20 43 34 19 40 25 54 5 47 5 36 21 6 18 29 26 56 23 2 28 20 28 14 20 53 47 17 15 19 7 40 6 38 24 9 42 20 23 51 28 38 53 58 20 23 16 19 6 19 32 24 23 17 8 26 27 12 23 23 14 20 57 55 19 34 15 47 6 50 19 39 23 38 17 51 23 13 30 15
And what I came up with at 0.37 MIPS for 10 hours. The Acer is locked up right now.
Score: 24554.32 Ioc: 0.05236 Ngram size: 4.5 Ngrams: 203 PC-cycles: 2 MPLYWILLL (749) M (0) PDDSOMEWH (723) WB (0) ULLASALSF (646) DCOM (116) OFANBORDE (674) WHING (232) ODYOFHAND (688) ENGAGOV (453) BLANCEDLA (705) GAILDBEL (465) TONEINGAP (776) IRISINOUR (713) GYSTALLC (597) AM (0) DIDISRIC (527) VSH (31) SSESOLUT (626) RUGDI (161) YLEDTHEY (680) ENKROY (233) HBEFORAL (683) ATOURMIN (616) INDPROVI (629) DBETHEYI (676) AEXISMTR (486) MOINGMR (393) HTCHOFW (438) NBUYOU (315) LOCKM (205) MTOL (102) WDGF (41) RLS (35) HE (0) F (0) S (0) WPCR (62) URTKNOWWHATCANDMC (1773) EHD (29) J (0) LMOREOFWHENINGBY (1720) HTHRUE (246) TDOITATETHEOT (1346) SCANGEING (753) BETATIONET (936) FFERENTSLOOK (1249) TTHEYPU (521) ICTESTITISATRIC (1484)
I didn’t see a lot of big words though.
Here is the mirrored.
31 60 8 56 11 44 37 101 1 4 5 11 32 4 53 102 3 3 55 25 11 16 50 8 51 50 2 8 37 21 10 26 33 3 103 48 36 53 25 7 61 16 22 40 43 56 14 11 3 52 61 5 16 22 57 3 46 62 27 9 63 40 59 6 51 37 29 20 104 58 51 37 42 31 20 42 29 31 30 51 40 55 63 40 59 30 49 7 35 18 36 21 26 7 56 50 34 36 38 33 37 8 61 18 41 54 40 1 51 15 39 36 50 30 48 38 29 5 17 105 106 21 37 27 41 107 41 50 39 48 40 108 36 44 109 5 23 3 49 31 44 44 46 36 12 45 20 31 51 36 46 16 6 110 5 58 30 1 111 21 35 18 63 34 62 27 36 55 48 43 34 56 54 6 5 47 32 42 29 13 28 10 50 30 112 20 2 13 4 9 45 39 22 4 11 16 113 5 15 23 5 21 53 114 21 25 7 10 115 33 26 8 31 22 28 10 16 40 29 11 41 31 13 32 14 16 17 13 33 55 11 33 1 3 52 51 15 18 51 116 11 11 22 7 12 28 36 117 3 5 20 118 54 25 40 119 34 43 20 14 11 16 53 20 13 26 10 37 6 21 36 5 47 5 47 53 20 14 28 20 28 2 23 56 26 29 18 9 24 38 6 40 7 120 15 17 23 20 58 53 38 28 51 23 20 42 12 27 26 8 17 23 24 32 121 6 122 16 123 55 57 20 14 23 23 15 30 13 23 51 17 38 23 39 124 50 6 47 15 34
And the results at 0.37 MIPS for 11 hours.
Score: 24583.07 Ioc: 0.05325 Ngram size: 4.5 Ngrams: 236 PC-cycles: 2 UYSTOPICK (759) P (0) UOEPITLLH (508) SO (0) RESSEDSIF (712) MICL (92) BETISTORD (732) WITGO (221) LYOURDALP (664) VELYWOO (462) SIONEDSID (698) UNDOURSW (591) HYWORSTAN (769) TFITTERTH (796) CISONLYW (627) KS (0) ENTEREHO (609) UCK (41) YFIELDLE (552) NEWIT (266) PQUALSUP (550) PPTHAN (354) USTPRODU (641) DRKOFANY (517) RVETHEIR (717) TYOUVEDO (623) GAMERAND (682) GPLANDP (470) ORQUEAU (372) FIFFST (236) MACIS (220) UDAM (91) RWOO (92) LUG (33) EG (0) R (0) C (0) GCHO (98) CKLYSENSTOODTHATW (1763) LUN (36) X (0) YSWERINGORINGIMI (1656) OFTUVU (146) VINGANADATION (1349) LSHOWTHEC (813) ANDIHASAND (868) HEISCASEYOUR (1189) CHANGAA (462) ERGASCHANGEOVER (1485)
I expanded the + symbol in all of the above. Again, no big words, and no particular order of rows.
So, what about those 48 cells highlighted for P16, P32, and P48 unigram repeats? The clusters around the pivots?
I made 1000 cryptograms, no transposition, but all with exactly 63 symbols, each key individualized and specific with my new encoder to make 63. I tested and shaped the keys to closely approximate the symbol count distribution with chi squared. I included one polyphone close as possible to 24 count. All from Classic American Short Stories from 20 stories and 20 different authors from the 1920s to the 1960s. Of 1000, only 14 delivered 48 cells highlighted at P 16, P36, and P48 unigram repeats. Here is the graph. I rounded to nearest even number, and x axis is count of cells highligted with y axis number of messages with that count.
So, is the P16 RLBT statistic meaningful or not? Here is the spike.
EDIT: I used ABAB and randomization matrix
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25
25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25
25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25
25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25
25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25
25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25
25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25
25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25
25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25
25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25
50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50
50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50
50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50
50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50
50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50
EDIT: I deleted the typical key it is uneccessary.
I recently wrote a thing that tries to guess word breaks and here’s what it got for your solves:
Test string: MPLYWILLLMPDDSOMEWHWBULLASALSFDCOMOFANBORDEWHINGODYOFHANDENGAGOVBLANCEDLAGAILDBELTONEINGAPIRISINOURGYSTALLCAMDIDISRICVSHSSESOLUTRUGDIYLEDTHEYENKROYHBEFORALATOURMININDPROVIDBETHEYIAEXISMTRMOINGMRHTCHOFWNBUYOULOCKMMTOLWDGFRLSHEFSWPCRURTKNOWWHATCANDMCEHDJLMOREOFWHENINGBYHTHRUETDOITATETHEOTSCANGEINGBETATIONETFFERENTSLOOKTTHEYPUICTESTITISATRIC
Guessed breaks: MPLY WILL LMPDD SOME WHW BULL AS ALSFDCOM OF AN BORDE WHING ODY OF HAND ENGAGOV BLANCED LAGAILD BELT ONE IN GAPIR IS IN OUR GY ST ALL CAM DID IS RICVSHSSE SOLUTRUGDIY LED THEY EN KROYH BE FOR AL AT OUR MININD PROVID BE THEY I A EXISM TRMOING MR HTCH OF WNBU YOU LOCK MMTOLWDGFRL SHE FSWPCRURT KNOW WHAT CAND MCEHDJL MORE OF WHEN ING BY H THRUET DO IT ATE THE OTS CAN GEING BETATION ETFFERENTS LOOK T THEY PUICT EST IT IS A TRIC
Test string: UYSTOPICKPUOEPITLLHSORESSEDSIFMICLBETISTORDWITGOLYOURDALPVELYWOOSIONEDSIDUNDOURSWHYWORSTANTFITTERTHCISONLYWKSENTEREHOUCKYFIELDLENEWITPQUALSUPPPTHANUSTPRODUDRKOFANYRVETHEIRTYOUVEDOGAMERANDGPLANDPORQUEAUFIFFSTMACISUDAMRWOOLUGEGRCGCHOCKLYSENSTOODTHATWLUNXYSWERINGORINGIMIOFTUVUVINGANADATIONLSHOWTHECANDIHASANDHEISCASEYOURCHANGAAERGASCHANGEOVER
Guessed breaks: UYS TO PICK PUOEPITLLH SO RESSED SIF MICLBETIST ORD WIT GOL YOUR DALPVELY WOOSIONED SID UND OURS WHY WORST ANT FITTER TH C IS ONLY WKS ENTERE HOUCKY FIELD LENE WITPQUAL SUPPP THAN UST PRODUDRK OF ANY RVE THEIR T YOUVE DOG AMER AND G PLAND POR QUE AUFIFF ST MACISUD A MR WOOLUGE GRCGCHOCKLY SEN STOOD THAT WLUNXYS WERING ORING I MIOFTUVUVING AN ADATION L SHOW THE CAND I HAS AND HE IS CASE YOUR CHANG A AER GAS CHANGE OVER
MPLY WILL LMPD D SOME WHW BULL AS ALSF
DCOMOFANBORDE WHIN GOD Y OF HAND
ENGAGO VBLANCEDLA G AILD BEL TONE IN GAPIR IS IN OUR GY STALL CAM
DID IS RICV SHSSE SOLUTRUGDIY LED THEY
ENKROYH BE FOR ALA TOUR MININD PROVID BE THEY IAEXISMTRMOING MR
HTCHOFW NBU YOU LOCK MMTOL WDGFRL SHEFSWPC
RURT KNOW WHAT CAN DMCEHDJL MORE OF WHEN INGBY
H THRU ET DO IT AT ETHEOTS CAN GEING BETATIONET
F FEREN TS LOOK T THEY PUIC TEST IT IS A TRIC
using the neck top computer gets a similar result to Doranchaks programme.
cheers
Thanks for taking a closer look. The fragments could need to be re-arranged because it is rows bound, however. But I don’t see any big words or context here anyway.
American Short Stories has 127 messages with one pivot, and 17 messages with two pivots in the plaintext, not transposed.
Then I inscribed the messages into this grid, P16 diagonally up LRBT.
001 003 006 010 015 021 028 036 045 055 066 078 091 105 120 136 153
002 005 009 014 020 027 035 044 054 065 077 090 104 119 135 152 170
004 008 013 019 026 034 043 053 064 076 089 103 118 134 151 169 187
007 012 018 025 033 042 052 063 075 088 102 117 133 150 168 186 204
011 017 024 032 041 051 062 074 087 101 116 132 149 167 185 203 220
016 023 031 040 050 061 073 086 100 115 131 148 166 184 202 219 235
022 030 039 049 060 072 085 099 114 130 147 165 183 201 218 234 249
029 038 048 059 071 084 098 113 129 146 164 182 200 217 233 248 262
037 047 058 070 083 097 112 128 145 163 181 199 216 232 247 261 274
046 057 069 082 096 111 127 144 162 180 198 215 231 246 260 273 285
056 068 081 095 110 126 143 161 179 197 214 230 245 259 272 284 295
067 080 094 109 125 142 160 178 196 213 229 244 258 271 283 294 304
079 093 108 124 141 159 177 195 212 228 243 257 270 282 293 303 312
092 107 123 140 158 176 194 211 227 242 256 269 281 292 302 311 319
106 122 139 157 175 193 210 226 241 255 268 280 291 301 310 318 325
121 138 156 174 192 209 225 240 254 267 279 290 300 309 317 324 330
137 155 173 191 208 224 239 253 266 278 289 299 308 316 323 329 334
154 172 190 207 223 238 252 265 277 288 298 307 315 322 328 333 337
171 189 206 222 237 251 264 276 287 297 306 314 321 327 332 336 339
188 205 221 236 250 263 275 286 296 305 313 320 326 331 335 338 340
And I was very surprised that this actually greatly reduces the number of pivots. It is just the plaintext, not encoded.
There were only 54 messages with one pivot, and 1 messages with three pivots. So, writing diagonally reduces pivots, and does not make them more probable for some reason, irregardless of the encoding.