Here’s a thing I threw together quick to encode these types. I think it works, LOL!
http://bardstowncable.net/~xenex/hsc/
-glurk
That’s really cool, glurk – thanks for posting that!
I second that.
Here’s what I am working on for AZdecrypt. I am merging the polyphones [user] and [auto] solver into one selection. A window will pop up which will allow the user to change the mode of the solver (for example to Hafer shifts) and also the option to set the number of letters per symbols etc. In general the solver is now much easier to work with since you don’t have to pop up the Symbols and Solver options menu to change the relevant settings.
Yesterday I worked on optimizations for the polyphones solver and managed something like a 2x in general performance of the solver. Two of my big ideas failed and I was expecting allot more but for now it is okay.

Nice work, Jarlve!
Can you explain the difference between "user + extra letters" and "increment extra letters"?
Nice work, Jarlve!
Can you explain the difference between "user + extra letters" and "increment extra letters"?
Hoping that this UI update will explain itself:

The "User defined polyphones + extra letters" solver mode replaces the "Substitution + polyphones [auto]" solver currently available in AZdecrypt. In the current AZdecrypt the settings for this solver can be found in the Solver options menu:
(Substitution + polyphones [auto]) Extra letters: 5 (Substitution + polyphones [auto]) Increment extra letters: Yes
– In the current AZdecrypt the [auto] solver cannot mix with user defined polyphones through the Symbols menu so that’s an addition.
Say that the cipher has 63 symbols, then the solver will assign 5 extra letters to the symbols with a external hill-climber. Such that for example a symbol could now map to 2 letters instead of one, that is one extra letter so to say. After every restart of the external hill-climber the amount of extra letters is incremented by one. This solver/mode can be used for ciphers where there is some random/unknown amount of polyphones, such as with smokie’s wildcard ciphers.
It is not easy and I’m still working on this. I’ve optimized the solver to the point where I am happy for a first version and are now running through all 10 ciphers again with these optimizations and 6-grams. It looks like about 5 to 7 ciphers have solved, the unsolved ciphers will be ran through again with higher n-grams etc.
Hopefully all these 10 ciphers can be solved, after that I will move on the the Z340 and some other unsolved ciphers in my library.
Made this Chi^2 test:
QLILCWQEBPLUBIPBE RIBVPRPWYBZXQLKWK HJILOQKLPMXUSLVBY LGHCLDIODPHVCLOSF FQROBVLOOLRNLQJJI XVPBVWKHVHDFSHXZL ABODKDBQLQEHZLRAF XUSBUIRUXIIEROAHU PXOHPRLWXEOBWRCUD JHPKBDAPJDVYBDSSO LTXWRFROQBUPXQAFH QWUHPLCIODJHVLQFP YBUVPXFKQLYBGHPFU HGWEDWGBPFDKBOPXQ AFDUYHUPZLXIABABU WQEBFUFKYHQQLYBKH PVXKGBKGBXSLXOQRY OBDNRSQKHJLKRQRKB XKGIBBYIHQHVVZEFZ KZEDUXFQHULWHPRPQ Chi^2 versus English: -N/+N ---------------------------------- -0/+0: 3308.70 -1/+1: 415.82 -2/+2: 412.35 -3/+3: 29.02 <--- -4/+4: 374.44 -5/+5: 603.30 -6/+6: 633.46 -7/+7: 592.88 -8/+8: 590.30 -9/+9: 349.79 -10/+10: 315.32 -11/+11: 434.25 -12/+12: 779.70 -13/+13: 1736.88 -14/+14: 1174.93 -15/+15: 420.33 -16/+16: 308.45 -17/+17: 333.53 -18/+18: 702.15 -19/+19: 713.55 -20/+20: 626.94 -21/+21: 586.85 -22/+22: 354.43 -23/+23: 29.99 -24/+24: 414.53 -25/+25: 361.29
Nice progress!
I just checked my ciphers again and, oops, I accidentally included one that was in French but didn’t notice it. Sorry about that. They were random samples from what I thought was an English corpus but apparently some French got through. This is the cipher encoded from French plaintext:
H.5A)CA1GG6BW-dTN 9LDVc.DzTf%|pLCN1 j%c41<LG<4*XO5bE. _(Y)(@SBdW1.LL7c. E._XS6WC.ct&jEPG. 6LtcW&*.d;4SCUtk: W-.1.&BYBdD<AkNS. Y#bCJP>.V(W<Fl6_H A^;END;(.RKNd&Y;/ pSOPd*j;(.-L:39Ap 7PPPZEd*MN1Ej*b1+ M44/LH;17P;Od.PG8 SJV.S&N^W.1_ZtW_( &D5J)8y;WT;&T>Y_j )fy4M.39%;Oj:C;OY S&ZlP6W;O_T;qG.Df &Z.SfFlf;E*E*Sc). -(b3+OWL/DB.;b6z+ f.)-.OqEd;Ed4L@<E >+CM.NS7|N2XYVD3@
Let me know if you want the plaintext as well, unless you prefer to try to get your solver to recover it.
All the rest are in English, so I wonder why they are harder than the others to solve.
– In the current AZdecrypt the [auto] solver cannot mix with user defined polyphones through the Symbols menu so that’s an addition.
Say that the cipher has 63 symbols, then the solver will assign 5 extra letters to the symbols with a external hill-climber. Such that for example a symbol could now map to 2 letters instead of one, that is one extra letter so to say. After every restart of the external hill-climber the amount of extra letters is incremented by one. This solver/mode can be used for ciphers where there is some random/unknown amount of polyphones, such as with smokie’s wildcard ciphers.
Thanks for the explanations. So, in the "user defined + extra" mode, the solver will automatically try up to 5 extra letters, except for symbols that have fixed polyphone counts supplied by the user?
I just checked my ciphers again and, oops, I accidentally included one that was in French but didn’t notice it. Sorry about that. They were random samples from what I thought was an English corpus but apparently some French got through. This is the cipher encoded from French plaintext:
Thanks for clearing that out, only 3 ciphers left to solve now. Yes, I would like to see the plain text for this one, here is the best solve I have for this cipher:
PEVENTERMINGSCREE LSACHEATEDTHISTER ATHERMOMMEWEBVIPA CKINKINGNORESOTHE PAYERNOTEDTHATSMA NSTHODWARSENTSTHU SCAREDGIGNAMEHERE IFITISLACKSMANNYP ERSPEASKAQUERHISK INFORWASKACOUPLEI TSSOSTRAWERPAWIRE WEEKSPORTSOFRESIG NICANDERSARYSTOCK HAVINGJOSESHELICA NDJEWELLTOFAUTOFI NDSNONSOFYESUMEAD DSANDANDSTATANDNE CKILEBOOKAGESINTE DANCEBUTNOTRESIMP LETWEENTHEREICALI
All the rest are in English, so I wonder why they are harder than the others to solve.
There is allot of variance in the solve times, some of them consistently solve in under a minute and other take hours. I have some ideas about the problem but it will take allot of time to find out.
Thanks for the explanations. So, in the "user defined + extra" mode, the solver will automatically try up to 5 extra letters, except for symbols that have fixed polyphone counts supplied by the user?
No, the 5 extra letters can also be distributed among the user defined polyphones.
Thanks for clearing that out, only 3 ciphers left to solve now. Yes, I would like to see the plain text for this one, here is the best solve I have for this cipher:
PEVENTERMINGSCREE LSACHEATEDTHISTER ATHERMOMMEWEBVIPA CKINKINGNORESOTHE PAYERNOTEDTHATSMA NSTHODWARSENTSTHU SCAREDGIGNAMEHERE IFITISLACKSMANNYP ERSPEASKAQUERHISK INFORWASKACOUPLEI TSSOSTRAWERPAWIRE WEEKSPORTSOFRESIG NICANDERSARYSTOCK HAVINGJOSESHELICA NDJEWELLTOFAUTOFI NDSNONSOFYESUMEAD DSANDANDSTATANDNE CKILEBOOKAGESINTE DANCEBUTNOTRESIMP LETWEENTHEREICALI
Here it is:
REQUIRENTTRSINSTA MMENTOULTRELACRAN CEDUDICTSETONQUIE STOITAUSSYDEMMEDE SECOURIRETASSISTE RMADICTESOEURLARO YNEDESCOSSESURQUO YJERESPONDISLARCH EVESQUEDEGLASCOET AUDICTSETONCOMMEA USSIFISTMADICTEDA MEETMREDESONCOSTQ UENOUSAVIONSFAICT CEQUIAVOITESTPOSS IBLECOMMEENCORENO USFAIRIONSTOUJOUR SPOURLARESTITUTIO NDEMADICTESOEURLA ROYNEDESCOSSEMAIS PARCEQUELAROYNEMA
There is allot of variance in the solve times, some of them consistently solve in under a minute and other take hours. I have some ideas about the problem but it will take allot of time to find out.
I am wondering about the key space.
Normally it’s just 26^63.
But with, say,13 possible N values, and 2 choices (+/-) for each of 340 plaintext positions, it jumps to:
(26^63) * 13 * (2^340).
If I’m not mistaken, that 2^340 factor is 16 trillion times the original keyspace of 26^63.
Or put another way, 2^340 is roughly the same as 26^72.
It seems quite amazing that your solver can crack these given how much harder the problem is!
Also, if the message is very long, that 2^L factor gets even bigger (where L is the message length).
So would a longer message be even harder to crack?
I am wondering about the key space.
Normally it’s just 26^63.
But with, say,13 possible N values, and 2 choices (+/-) for each of 340 plaintext positions, it jumps to:
(26^63) * 13 * (2^340).If I’m not mistaken, that 2^340 factor is 16 trillion times the original keyspace of 26^63.
Or put another way, 2^340 is roughly the same as 26^72.
It seems quite amazing that your solver can crack these given how much harder the problem is!
Also, if the message is very long, that 2^L factor gets even bigger (where L is the message length).
So would a longer message be even harder to crack?
(26^63)*13*(2^340) is about the same as 26^136 or a 0.4 multiplicity cipher.
– Though within the 13 there are equivalences, for example -3/+3 M:KQ and -10/+10 A:QK. In short -3/+3 and -10/+10 share the same alphabet when substitution is factored in.
– And the homophonic substitution layer will sort of diffuse the 2^340 and there will be allot of homophones which have a 1:1 mapping. For the 6 ciphers that have solved the solver uses about 80 to 90 symbols instead of the full 63*2.
It seems reasonably to me that a longer message with the same multiplicity is harder to crack because of the increased 2^L factor you mention. Even outside of this hypothesis longer (versus shorter) ciphers with the same multiplicities are harder to crack.
Some good new, I just made a optimization that reduced average solve times by a factor of 3. It is funny how it goes sometimes. When I first made the Hafer solver the 10th cipher you shared had a average solve time of 2 hours, which I took down to about 20 minutes, then 5 minutes, then 2 minutes, then 1 minutes, then 30 seconds and now it’s under 10 seconds! So happy, this is gonna help allot with the 3 remaining unsolved ones.
It seems reasonably to me that a longer message with the same multiplicity is harder to crack because of the increased 2^L factor you mention. Even outside of this hypothesis longer (versus shorter) ciphers with the same multiplicities are harder to crack.
So for longer ciphers, it might be better to split them into smaller ones since they might solve more easily. If so, I wonder if a "sweet spot" can be determined. I.e., the most efficient place(s) to split up the cipher for separate solves.
Some good new, I just made a optimization that reduced average solve times by a factor of 3. It is funny how it goes sometimes. When I first made the Hafer solver the 10th cipher you shared had a average solve time of 2 hours, which I took down to about 20 minutes, then 5 minutes, then 2 minutes, then 1 minutes, then 30 seconds and now it’s under 10 seconds! So happy, this is gonna help allot with the 3 remaining unsolved ones.
Wow – as usual, you are the king of optimization! Nice work.
OK so I believe the general equation for equivalent multiplicity for the Hafer homophonic ciphers is:
log26((26^63) * 13 * (2^L))/L
It actually decreases as L increases, if my math is right.
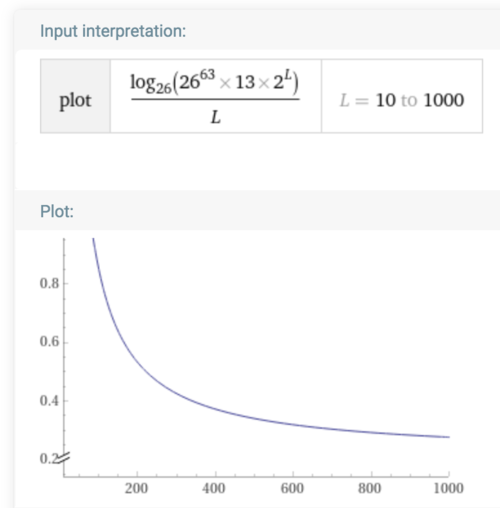
And as L approaches infinity, the limit goes to log(2)/log(26) = 0.21.
So that’s the smallest achievable multiplicity for this kind of cipher (with a homophonic alphabet size of 63, plaintext alphabet size of 26, and shifts taken from the range [1,13]).
That means longer ciphers should still be easier to solve, I guess.
Here’s a thing I threw together quick to encode these types. I think it works, LOL!
http://bardstowncable.net/~xenex/hsc/
-glurk
I mirrored it here:
http://zodiackillerciphers.com/hafer-shift-cipher/
So for longer ciphers, it might be better to split them into smaller ones since they might solve more easily. If so, I wonder if a "sweet spot" can be determined. I.e., the most efficient place(s) to split up the cipher for separate solves.
I don’t think it is the case for any substitution cipher. I meant that if you have cipher A with length 100 and multiplicity 0.4 and cipher B with length 200 and multiplicity 0.4 then cipher B will be harder than cipher A. Probably simply because cipher B will have many more symbols to work out, it has a larger search space.
OK so I believe the general equation for equivalent multiplicity for the Hafer homophonic ciphers is:
log26((26^63) * 13 * (2^L))/L
Heh, I never thought of using log in this way. I’d say that it’s the upper bound multiplicity.
And as L approaches infinity, the limit goes to log(2)/log(26) = 0.21.
So that’s the smallest achievable multiplicity for this kind of cipher (with a homophonic alphabet size of 63, plaintext alphabet size of 26, and shifts taken from the range [1,13]).
With 13 both shifts point to the same letter right?
With 13 both shifts point to the same letter right?
Yes, good point. It would be just a ROT13+Homophonic instead of a Hafer Homophonic.
So we only have to consider N taken from [1,12].
Not much effect on equivalent multiplicity for L=340.
0.40028 instead of 0.40036.
It is not easy and I’m still working on this. I’ve optimized the solver to the point where I am happy for a first version and are now running through all 10 ciphers again with these optimizations and 6-grams. It looks like about 5 to 7 ciphers have solved, the unsolved ciphers will be ran through again with higher n-grams etc.
Only one cipher remains unsolved now. That’s good because it can now be focused upon. I will again look for optimizations this weekend and start the attack on the last cipher monday.
