I did two series of tests, which were actually created out of playing around. Nevertheless I want to document the results for completeness. I also noticed two rather bizarre nGram repetitions during the tests. But more about that at the end of the thread.
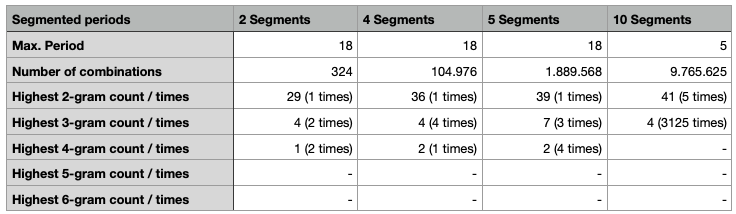
Segmented periods:
The basic idea is not new, but I wanted to examine this again. z340 could, just like z408, consist of several segments. But unlike z408, these could have been encrypted separately. Assuming that each segment is the same size, there are four possibilities: Two parts with 10 lines each, 4 parts with 5 lines each, 5 parts with 4 lines each or 10 parts with 2 lines each. If you assume "period n" as the transposition method, then the individual segments could have been transposed with different periods. Example:
Segment size 4: First quarter of z340 was transposed with period 8, the second quarter with period 3, the third quarter with period 10 and the last quarter with period 19
In my test I went through all segment sizes and tried all combinations of periods. For the segment sizes 2, 4 and 5 I used a maximum of period 18, for segment size 10 only period 5. I did not send the results through my solver, but only determined the maximum number of repeating nGrams. Here is the result:
Explanation: "7 (3 times)" in line 4 means, for example, that the highest number of repeated trigrams was 7. This was the case in 3 of the 1,889,568 tests.
At first I was surprised that the number of repeating nGrams increases with the number of segments. However, the explanation is rather simple: The more segments, the more tests. So the probability simply increases.
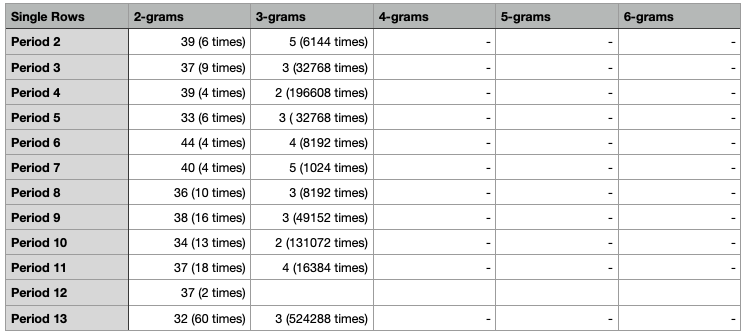
Single rows period transposition:
For this test I wanted to know what happens when you apply period n per row, not to whole blocks. For example the row 5, 6, 9, 12, 17 and 20 each with period 5 untranspose. To make it clear: I do not think that z340 was transposed in such a way. I just want to know what effect this has. There are 1,048,576 possible combinations of transposed and unchanged row (2^20, alternatively "20 bit"). I checked these combinations with the periods 2 to 9 for nGram repetitions. Here is the result:
Explanation: "40 (4 times)" in line 6 means for example with period 7 a maximum of 40 repeated bigrams were found. This was the case in 4 of 1,048,576 tests.
I find it interesting that there were no repeated 4grams (or larger) in any of the 8,388,608 tests. This could be a good indication that z340 is based on a continuous and regular transposition. Transpositions such as spiral, segmented or railfence should behave completely different in such a test. But this is only a first thought, I am not sure yet.
nGram curiosities:
While running the shown test series I noticed two ciphers which are quite remarkable:
6-gram:
If you apply "untranspose period 10" to row 1-4 and row 17-20, you will obtain a repeated 6gram.
A repeated 6gram is already very rare. That you can create it in a comparatively simple way is quite curious.
4-grams directly below each other:
First, apply "untranspose period 5" to the first 5 row of z340 (each row separately, not all in one step). Then apply utp 74 to the whole result, resulting in a repeated 4gram. This alone is not astonishing. But the fact, that the two are directly under each other is. This is probably more a coincidence than the just shown 6gram. Nevertheless I did not want to leave it undocumented.
I will run these tests again soon. But then with the first 340 characters of z408, which were transposed with period 19 before. Let’s see how the results differ.
One more thought:
A high number of repeating nGrams is of course no indication that we are getting closer to the goal. However, I’m beginning to think that z340 simply has too many surprises in this direction. Especially the 6gram shown above and the 48/8 phenomenon (created by various shifting operations) make me feel confused. For 340 characters and 63 different symbols there are an unusually high number of nGram phenomena. I’m very surprised that we still don’t have a hint of at least a partial solution. I wouldn’t be surprised if the "plaintext" of z340 consisted of a creative pattern of plaintext letters instead of a meaningful text.
Translated with http://www.DeepL.com/Translator (free version)
Thanks for doing this test Largo.
What are the odds of a having a repeated 6-gram with Z340 shuffles?
I will run these tests again soon. But then with the first 340 characters of z408, which were transposed with period 19 before. Let’s see how the results differ.
Results should on average be a bit weaker due to the lower IOC of the Z408. Unless the bigram repeats at period 1 shine through somehow due to the design of the test.
Think it would be better if you pick a shuffled Z340 instead.
What are the odds of a having a repeated 6-gram with z340 shuffles?
I have shuffled z340 3 million times. Repeated 6-grams were found in 12 ciphers. This corresponds to a probability of 0.0004%.
Cool experiments, Largo!
What are the odds of a having a repeated 6-gram with z340 shuffles?
I have shuffled z340 3 million times. Repeated 6-grams were found in 12 ciphers.
At period 10? Or any period?
At period 10? Or any period?
Any period. If I shuffle z340 and then un-transpose p10 again, it is the same as shuffle twice. Or am I just wrong? In which way is it statistically relevant, if I run period n again on an cipher that is already shuffled? The same applies to untranspose original z340 and then shuffle it, doesn’t it?
At period 10? Or any period?
Any period. If I shuffle z340 and then un-transpose p10 again, it is the same as shuffle twice. Or am I just wrong? In which way is it statistically relevant, if I run period n again on an cipher that is already shuffled? The same applies to untranspose original z340 and then shuffle it, doesn’t it?
I’m not sure what the best approach would be.
Does the 6-gram you find only show up when you un-transpose individual segments, rather than the entire cipher?
I guess when it comes to finding a 6-gram repeating at period 10 in Z340 when considering segments, I’m most interested in the question: How often can a repeating 6-gram be found at any period in shuffles of Z340 when considering segments? So, my instinct would be to look in shuffles for repeats at any period in any possible segment, to get a sense of truly rare that event would be when compared to noise.
So, my instinct would be to look in shuffles for repeats at any period in any possible segment, to get a sense of truly rare that event would be when compared to noise.
Here are the results for comparison. First, z340 was shuffled and then all combinations of segmented periods were tested.
The shuffled version generates significantly less nGrams than the original z340. I will do more tests with segments. The found 6-gram looks quite interesting for me.
Here are the results for comparison. First, z340 was shuffled and then all combinations of segmented periods were tested.
The shuffled version generates significantly less nGrams than the original z340. I will do more tests with segments. The found 6-gram looks quite interesting for me.
Very interesting! How many shuffles was that? Is it just one shuffle but with all the combinations tested?
The periodic behavior in Z340 appears to be a real phenomenon based on this and many other tests.
If Z340 was gibberish, how did he make the ciphertext periodic in nature? Seems like he would have had to make a scrambled/random plaintext and encode it with some periodic scheme.
That is one of the things that still makes me think there is a coherent plaintext somewhere in there.
Very interesting! How many shuffles was that? Is it just one shuffle but with all the combinations tested?
Yes
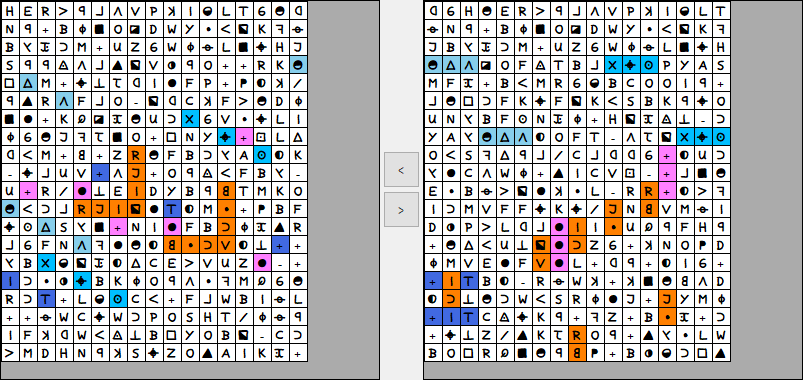
Here is another strange transposition: Shift the whole cipher to the right (offset column order 1). Then UTP 15 row 1 and UTP 19 rows 4-20. You get 47 bigrams and this strange pattern:
I know this is not exactly an academic approach. Rather, I simply experiment. I look for the needle in the haystack by throwing myself into it again and again and wait until it stings.