There is this little list of bigram peaks that stem from the period 19 bigram peak that I consider, for what it is worth, to be the "special bigram peaks":
1. Offset row order 18 + untranspose period 19: 41 bigrams.
2. Offset column order 1 + untranspose period 19: 45 bigrams.
3. Transpose period row order 2 + untranspose period 36: 41 bigrams.
4. Untranspose period column order 2 + untranspose period 18. 44 bigrams. (found by doranchak)
For special bigram peak 1 and 2 the actual offset value does not matter as long as it is not 0. The observation is that it a higher bigram peak is recorded at values other than 0.
I believe that these may be connected to a specific type of period 19 transposition. Likely some sort of 2-dimensional period in a grid. Significance wise, if we consider many randomizations of the 340 and find the highest bigram result in the set "period 1 to 170" for each randomization, the bigram peak of 37 at period 19 has a 3.56 sigma (standard deviations). The reason why I did not include periods over 170 (half of 340) is that these are coarse rearrangements of period 1. A 7.00 sigma was recorded for the bigram peak of 45 for offset column order 1 + untranspose period 19 by finding the highest bigram result in the set "offset column order 0 to 16 times period 1 to 170" for each randomization.
To start, here is an example cipher of a 2-dimensional period in a grid transposition based on the 21 by 21 magic square found in the Zodiac FBI files. It has a period 19 bigram peak of 40, a offset row order + untranspose period 19 bigram peak of 41, a offset column order 5 + untranspose period 19 bigram peak of 47 and a untranpose period column order 2 + untranspose period 18 bigram peak of 43. In short, it typically has 3 of the 4 special bigram peaks by default:
_)-"I3^G#-F.OR3%! S=!&0MO?.#9@C82>' ,Q57_=_R(&/HU@DIN 4-3-F0:!YO)[%#(Q C.7S$E@)I;!+=Z3]8 X-"^7-I_&0RB3!=O !9Q?PF%@1C5=Z8-"4 97Y_65%./]25_==IN &3Z'-[R"K!X>%_BG= #&9YQ5?YJO!7">2" 3UH>9J,4;-C$S"APZ %8WR-+J_A-O6[C=L- #1YRQ5NV7>-'W/"!9 !MZ(0=)I3@;]Y#DP JQ_7L&O-TPN--+$_A >-@8G%!=@IIA<S&' W-V1/-K3W=!.5X!$ #Q7E%8YBI?39O=5C! F.42[0SAZ"*90'>!# 5$_WQ"6X.":<V&A,
AZdecrypt detail of the special bigram peaks of the 340 (secondary periods not shown):
Offset row order: (transposition) -------------------------------------------------------- Offset row order 0: 37 Offset row order 1: 37 Offset row order 2: 38 Offset row order 3: 38 Offset row order 4: 37 Offset row order 5: 36 Offset row order 6: 37 Offset row order 7: 34 Offset row order 8: 35 Offset row order 9: 36 Offset row order 10: 40 Offset row order 11: 39 Offset row order 12: 34 Offset row order 13: 34 Offset row order 14: 37 Offset row order 15: 37 Offset row order 16: 38 Offset row order 17: 40 Offset row order 18: 41 <--- Offset row order 19: 37 -------------------------------------------------------- Transposition average: 37.1 Offset column order: (transposition) -------------------------------------------------------- Offset column order 0: 37 Offset column order 1: 45 <--- Offset column order 2: 40 Offset column order 3: 36 Offset column order 4: 35 Offset column order 5: 35 Offset column order 6: 35 Offset column order 7: 33 Offset column order 8: 34 Offset column order 9: 36 Offset column order 10: 35 Offset column order 11: 38 Offset column order 12: 37 Offset column order 13: 37 Offset column order 14: 37 Offset column order 15: 33 Offset column order 16: 34 -------------------------------------------------------- Transposition average: 36.29 Period row order: (transposition, untransposition) -------------------------------------------------------- Period row order 1: 37, 37 Period row order 2: 41, 34 <--- Period row order 3: 35, 34 Period row order 4: 32, 32 Period row order 5: 32, 32 Period row order 6: 35, 33 Period row order 7: 34, 35 Period row order 8: 34, 33 Period row order 9: 34, 35 Period row order 10: 34, 41 <--- Period row order 11: 34, 34 Period row order 12: 32, 35 Period row order 13: 39, 33 Period row order 14: 35, 31 Period row order 15: 34, 33 Period row order 16: 31, 32 Period row order 17: 37, 32 Period row order 18: 35, 33 Period row order 19: 36, 35 -------------------------------------------------------- Transposition average: 34.78 Untransposition average: 33.89 Period column order: (transposition, untransposition) -------------------------------------------------------- Period column order 1: 37, 37 Period column order 2: 35, 44 <--- Period column order 3: 38, 37 Period column order 4: 33, 31 Period column order 5: 33, 32 Period column order 6: 37, 38 Period column order 7: 34, 31 Period column order 8: 35, 31 Period column order 9: 44, 35 <--- Period column order 10: 37, 33 Period column order 11: 35, 37 Period column order 12: 35, 31 Period column order 13: 34, 34 Period column order 14: 32, 32 Period column order 15: 32, 31 Period column order 16: 32, 35 -------------------------------------------------------- Transposition average: 35.18 Untransposition average: 34.31
There is this little list
Coincidence or intention? This is not the first reference to certain letters in your posts ![]()
I believe that these may be connected to a specific type of period 19 transposition. Likely some sort of 2-dimensional period in a grid.
Could you describe this in more detail, please? I’m not quite sure what a two-dimensional transposition is. Do you mean shifting the whole cipher left/right and up/down?
The reason why I did not include periods over 170 (half of 340) is that these are coarse rearrangements of period 1
For the same reason, the default setting of my statistics tool is also 170 ![]()
To start, here is an example cipher of a 2-dimensional period in a grid transposition based on the 21 by 21 magic square found in the Zodiac FBI files. It has a period 19 bigram peak of 40, a offset row order + untranspose period 19 bigram peak of 41, a offset column order 5 + untranspose period 19 bigram peak of 47 and a untranpose period column order 2 + untranspose period 18 bigram peak of 43.
Unfortunately, I cannot reproduce the Bigram peak 47. Just shift 5 columns upwards?
I haven’t dealt with the magic square in detail yet. I just remember you mentioning it in one of your posts.
Do you remember my discovery with 48 bigrams and 8 trigrams? (viewtopic.php?f=81&t=3196&start=720#p55478)
You may try the following:
Shift your sample cipher 5 to the right and 8 up: 47 bigrams and 6 trigrams on P19. Second example… 5 to the right and 6 down: 46 bigram and 7 trigrams at P19.
Your discovery of the connection to Magic Square is really interesting!
Could you describe this in more detail, please? I’m not quite sure what a two-dimensional transposition is. Do you mean shifting the whole cipher left/right and up/down?
Where the period has a x and y component to it, go left by 2 and down by 1 etc.
Simple example matrix:
1 61 121 181 241 301 21 81 141 201 261 321 41 101 161 221 281 222 282 2 62 122 182 242 302 22 82 142 202 262 322 42 102 162 103 163 223 283 3 63 123 183 243 303 23 83 143 203 263 323 43 324 44 104 164 224 284 4 64 124 184 244 304 24 84 144 204 264 205 265 325 45 105 165 225 285 5 65 125 185 245 305 25 85 145 86 146 206 266 326 46 106 166 226 286 6 66 126 186 246 306 26 307 27 87 147 207 267 327 47 107 167 227 287 7 67 127 187 247 188 248 308 28 88 148 208 268 328 48 108 168 228 288 8 68 128 69 129 189 249 309 29 89 149 209 269 329 49 109 169 229 289 9 290 10 70 130 190 250 310 30 90 150 210 270 330 50 110 170 230 171 231 291 11 71 131 191 251 311 31 91 151 211 271 331 51 111 52 112 172 232 292 12 72 132 192 252 312 32 92 152 212 272 332 273 333 53 113 173 233 293 13 73 133 193 253 313 33 93 153 213 154 214 274 334 54 114 174 234 294 14 74 134 194 254 314 34 94 35 95 155 215 275 335 55 115 175 235 295 15 75 135 195 255 315 256 316 36 96 156 216 276 336 56 116 176 236 296 16 76 136 196 137 197 257 317 37 97 157 217 277 337 57 117 177 237 297 17 77 18 78 138 198 258 318 38 98 158 218 278 338 58 118 178 238 298 239 299 19 79 139 199 259 319 39 99 159 219 279 339 59 119 179 120 180 240 300 20 80 140 200 260 320 40 100 160 220 280 340 60
More complicated example matrix:
133 261 117 245 101 229 85 213 1 197 325 181 309 165 293 149 277 150 278 134 262 118 246 102 230 18 214 2 198 326 182 310 166 294 167 295 151 279 135 263 119 247 35 231 19 215 3 199 327 183 311 184 312 168 296 152 280 136 264 52 248 36 232 20 216 4 200 328 201 329 185 313 169 297 153 281 69 265 53 249 37 233 21 217 5 218 6 202 330 186 314 170 298 86 282 70 266 54 250 38 234 22 235 23 219 7 203 331 187 315 103 299 87 283 71 267 55 251 39 252 40 236 24 220 8 204 332 120 316 104 300 88 284 72 268 56 269 57 253 41 237 25 221 9 137 333 121 317 105 301 89 285 73 286 74 270 58 254 42 238 26 154 10 138 334 122 318 106 302 90 303 91 287 75 271 59 255 43 171 27 155 11 139 335 123 319 107 320 108 304 92 288 76 272 60 188 44 172 28 156 12 140 336 124 337 125 321 109 305 93 289 77 205 61 189 45 173 29 157 13 141 14 142 338 126 322 110 306 94 222 78 206 62 190 46 174 30 158 31 159 15 143 339 127 323 111 239 95 223 79 207 63 191 47 175 48 176 32 160 16 144 340 128 256 112 240 96 224 80 208 64 192 65 193 49 177 33 161 17 145 273 129 257 113 241 97 225 81 209 82 210 66 194 50 178 34 162 290 146 274 130 258 114 242 98 226 99 227 83 211 67 195 51 179 307 163 291 147 275 131 259 115 243 116 244 100 228 84 212 68 196 324 180 308 164 292 148 276 132 260
Unfortunately, I cannot reproduce the Bigram peak 47. Just shift 5 columns upwards?
Column order, not row order. And I made an error, it is supposed to be 46.
Do you remember my discovery with 48 bigrams and 8 trigrams?
Ofcourse, do not worry about it.
Your discovery of the connection to Magic Square is really interesting!
Thanks!
Using the simple example matrix, a bigram peak at "4. Untranspose period column order 2 + untranspose period 18. 44 bigrams. (found by doranchak)" is easily explained as not random.
Consider the simple example matrix again (it has a 2-dimensional period rule, left by 2 and down by 1):
1 61 121 181 241 301 21 81 141 201 261 321 41 101 161 221 281 222 282 2 62 122 182 242 302 22 82 142 202 262 322 42 102 162 103 163 223 283 3 63 123 183 243 303 23 83 143 203 263 323 43 324 44 104 164 224 284 4 64 124 184 244 304 24 84 144 204 264 205 265 325 45 105 165 225 285 5 65 125 185 245 305 25 85 145 86 146 206 266 326 46 106 166 226 286 6 66 126 186 246 306 26 307 27 87 147 207 267 327 47 107 167 227 287 7 67 127 187 247 188 248 308 28 88 148 208 268 328 48 108 168 228 288 8 68 128 69 129 189 249 309 29 89 149 209 269 329 49 109 169 229 289 9 290 10 70 130 190 250 310 30 90 150 210 270 330 50 110 170 230 171 231 291 11 71 131 191 251 311 31 91 151 211 271 331 51 111 52 112 172 232 292 12 72 132 192 252 312 32 92 152 212 272 332 273 333 53 113 173 233 293 13 73 133 193 253 313 33 93 153 213 154 214 274 334 54 114 174 234 294 14 74 134 194 254 314 34 94 35 95 155 215 275 335 55 115 175 235 295 15 75 135 195 255 315 256 316 36 96 156 216 276 336 56 116 176 236 296 16 76 136 196 137 197 257 317 37 97 157 217 277 337 57 117 177 237 297 17 77 18 78 138 198 258 318 38 98 158 218 278 338 58 118 178 238 298 239 299 19 79 139 199 259 319 39 99 159 219 279 339 59 119 179 120 180 240 300 20 80 140 200 260 320 40 100 160 220 280 340 60
Untranspose period 19. see that the result has at most 9 numbers or so that correctly follow eachother, which is caused by mismatching different period 19 transposition systems. The goodness of the untransposition can be measured with my slope measurement inside AZdecrypt (only when it is numerical). Its slope is 263, normalized over the cipher length minus 1 gives us 0.77. It could be considered to be 77% good in some way.
1 2 3 4 5 6 7 8 9 231 232 233 234 235 236 237 238 120 61 62 63 64 65 66 67 68 290 291 292 293 294 295 296 297 298 180 121 122 123 124 125 126 127 128 10 11 12 13 14 15 16 17 239 240 181 182 183 184 185 186 187 69 70 71 72 73 74 75 76 77 299 300 241 242 243 244 245 246 247 129 130 131 132 133 134 135 136 18 19 20 301 302 303 304 305 306 188 189 190 191 192 193 194 195 196 78 79 80 21 22 23 24 25 26 248 249 250 251 252 253 254 255 137 138 139 140 81 82 83 84 85 307 308 309 310 311 312 313 314 315 197 198 199 200 141 142 143 144 145 27 28 29 30 31 32 33 34 256 257 258 259 260 201 202 203 204 86 87 88 89 90 91 92 93 94 316 317 318 319 320 261 262 263 264 146 147 148 149 150 151 152 153 35 36 37 38 39 40 321 322 323 205 206 207 208 209 210 211 212 213 95 96 97 98 99 100 41 42 43 265 266 267 268 269 270 271 272 154 155 156 157 158 159 160 101 102 324 325 326 327 328 329 330 331 332 214 215 216 217 218 219 220 161 162 44 45 46 47 48 49 50 51 273 274 275 276 277 278 279 280 221 103 104 105 106 107 108 109 110 111 333 334 335 336 337 338 339 340 281 163 164 165 166 167 168 169 170 52 53 54 55 56 57 58 59 60 222 223 224 225 226 227 228 229 230 112 113 114 115 116 117 118 119 282 283 284 285 286 287 288 289 171 172 173 174 175 176 177 178 179
Untranspose period column order 2. Part of special bigram peak number 4 as found by doranchak. Notice the increase in length of numbers that follow eachother correctly in a diagonal, it jumped from 9 to 17.
1 121 241 21 141 261 41 161 281 61 181 301 81 201 321 101 221 222 2 122 242 22 142 262 42 162 282 62 182 302 82 202 322 102 103 223 3 123 243 23 143 263 43 163 283 63 183 303 83 203 323 324 104 224 4 124 244 24 144 264 44 164 284 64 184 304 84 204 205 325 105 225 5 125 245 25 145 265 45 165 285 65 185 305 85 86 206 326 106 226 6 126 246 26 146 266 46 166 286 66 186 306 307 87 207 327 107 227 7 127 247 27 147 267 47 167 287 67 187 188 308 88 208 328 108 228 8 128 248 28 148 268 48 168 288 68 69 189 309 89 209 329 109 229 9 129 249 29 149 269 49 169 289 290 70 190 310 90 210 330 110 230 10 130 250 30 150 270 50 170 171 291 71 191 311 91 211 331 111 231 11 131 251 31 151 271 51 52 172 292 72 192 312 92 212 332 112 232 12 132 252 32 152 272 273 53 173 293 73 193 313 93 213 333 113 233 13 133 253 33 153 154 274 54 174 294 74 194 314 94 214 334 114 234 14 134 254 34 35 155 275 55 175 295 75 195 315 95 215 335 115 235 15 135 255 256 36 156 276 56 176 296 76 196 316 96 216 336 116 236 16 136 137 257 37 157 277 57 177 297 77 197 317 97 217 337 117 237 17 18 138 258 38 158 278 58 178 298 78 198 318 98 218 338 118 238 239 19 139 259 39 159 279 59 179 299 79 199 319 99 219 339 119 120 240 20 140 260 40 160 280 60 180 300 80 200 320 100 220 340
Untranspose period column order 2 + untranspose period 18. This is special bigram peak number 4 in a whole. It has a slope of 293, normalized over the cipher length minus 1 gives 0.86 or 86% good. So the goodness of the untransposition jumped from 77% to 86% and this is why bigrams increase over a regular period 19 untransposition. In short, we are combining transposition steps to approximate the transposition more closely.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 239 240 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 18 19 20 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 137 138 139 140 21 22 23 24 25 26 27 28 29 30 31 32 33 34 256 257 258 259 260 141 142 143 144 145 146 147 148 149 150 151 152 153 35 36 37 38 39 40 261 262 263 264 265 266 267 268 269 270 271 272 154 155 156 157 158 159 160 41 42 43 44 45 46 47 48 49 50 51 273 274 275 276 277 278 279 280 161 162 163 164 165 166 167 168 169 170 52 53 54 55 56 57 58 59 60 281 282 283 284 285 286 287 288 289 171 172 173 174 175 176 177 178 179 180 61 62 63 64 65 66 67 68 290 291 292 293 294 295 296 297 298 299 300 181 182 183 184 185 186 187 69 70 71 72 73 74 75 76 77 78 79 80 301 302 303 304 305 306 188 189 190 191 192 193 194 195 196 197 198 199 200 81 82 83 84 85 307 308 309 310 311 312 313 314 315 316 317 318 319 320 201 202 203 204 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 321 322 323 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 101 102 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 221 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 120
I was looking again at the last post of this thread, because I noticed some things during my experiments. I admit I haven’t dealt with it 100% before. But now I understand it and I especially like the idea of the transposition matrix (Thanks for the great explanation). I wrote a long answer, but I don’t want to post it yet, because there is still a lot missing.
So my question is this: I’m not quite clear about Magic Square yet. I know what a Magic Square is, but I don’t understand how you use it on a 17×20 cipher.
I can use this link ( http://www.keithschwarz.com/mathtricks/magic.php ) to create a 21×21 square, but that doesn’t help me at all. How did you proceed? How does this produce a 17×20 transposition matrix? I found the following thread, but that doesn’t help me either:
viewtopic.php?f=81&t=2617&p=41369#p41369. Something I miss here. May you explain how you create such a "magic" cipher? Thank you in advance
Translated with http://www.DeepL.com/Translator
Thanks for your interest. About the 21 by 21 magic square in the FBI Zodiac files, it is about its reading rule and in general not a magic square itself.
My observation is this:
1. When the reading rule of the magic square is applied to a 17 by 20 grid as a transposition it is period 19! The reading rule is a 2-dimensional periodical transposition system.
2. The reading rule produces some of the special bigram peaks as mentioned in the main post of this thread. More in general these special bigram peaks are a typical by-product of 2-dimensional periodical transposition systems.
Hypothesis:
Given the special bigram peaks, the 340 could be using a 2-dimensional periodical transposition system of some sort.
Open question:
The magic square seems to be a take on the siamese method https://en.wikipedia.org/wiki/Siamese_method though the siamese method is strictly diagonal. So far I have not been able to find a reference to the variation in the reading rule that was used for the 21 by 21 magic square. It could be worth to contact an expert on magic squares about this matter.
Okay, I’m afraid this is going to be a textwall…
It would indeed be very interesting to know why this Magic Square appears in the FBI files and what the background is. Is there any way to ask the guys directly? Will one of them remember anything after all these years? People are probably all retired anyway. I can try to find out something about the variation of the Magic Square.
… and now let’s see if I understood you correctly regarding the special bigram peaks:
You take a plain text and transpose it with your "simple example matrix". Let’s just say, just for fun, we can’t solve it after that and then take measurements. At some point we come across P19 and get many bigramms. However, the encryption cannot be solved because "untranspose P19" only finds partial correlations. One could say that P19 is "related" to the matrix, but it is not the solution. After a while we find out that period column order 2 + P18 results in even more bigramms. Unfortunately, this does not lead to a solution either. However, the peak can be explained by a better hit rate of the correct following characters. The correlation is better. So you are saying that the "special bigram peaks" are all indications of the actual transposition and we approach the final solution. Is that summarized correctly?
If so, some of my observations, which I thought to be coincidences, are explained by your idea. (Maybe they are coincidences anyway). To make the examples easier to explain, I’m assuming for fun that z340 was transposed with your "simple example matrix" and we just don’t know it.
PS: I will replace "untranspose perdiod column order" with "UPC", which is shorter.
If z340 is resized to 20×17 and then diagonal 1 untransposed, you get a lot of bigram repeats. No wonder, it’s just a disguised P19, which results in a slope of 261 in relation to the matrix. maybe we’re not closer to the solution, but it may simply match more characters of the original sequence.
"Untranspose P18" and "Untranspose Diagonal" are very similar, you can already see that in a purely visual way. No surprise, but a nice example of how different transpositions can point to the original transposition (or the wrong one).
If I shift columns 2 and 4 one character down on z340, I get 42 bigram and 4 trigrams on P19, I know that the matrix you show is only an example, but it fits by random here. Take columns 2 and 4 of your matrix and shift them down by one. The slope increases from 263 to 265 according to untransposed P19 and the first uninterrupted line goes from 1 to 11.
Let’s take this game a little further:
Shift Row 3 to the right by one and columns 2 and columns 4 to the bottom by one: 48 bigram, 5 trigrams! Coincidence? Maybe! But if you run the result with AZDecrypt’s transposition solver, you get a lot of results with a score of 21100 and more.
This is the cipher with shifted rows and columns:
HMRHbcdVPeIfLTGgh NE+ajkOlDWYmnoKpq JbrBtM+UZGWjqLkuH SBbsdcwoVxbO++RKg ybMvu12hI7FP+34e5 bzR+FcO-ohCeFagDj kw+dQl8gUtXGVmuLI j7gKp2kO+yNYu+9Lz hGMJ0+ZRgFBtrA#4K -nc+V+dJ+ObvnFBr- UuRU71EIDYBb0TMKO g+t5RJIo7T4Mm+3BF unzcrk+NI7FBtj8wR c#FSdp7g40mtV41++ rGXNos4zCEaVUZ7-+ IBmfuBKjObdmpMQGg RtTxLf#Cn+FcWBIqL +tq+CuWtPOSHT5jqb I+eWWnv1ByYOBo-Ct aFDhNbeSuZOwAIK8+
Maybe we can find a partial solve by such experiments and find the correct solution in a second step (that is what you are suggesting, right?)
Another example: Based on your matrix: UPC 2, then untransposed "diagonal 3" (AZDecrypt) the slope rises to 315. P18 is in principle diagonal 3, only the latter simply matches better.
This is interesting, too:
Take your Magic Square and complete number 4 of your list at the top of the thread (UPC 2 + untranspose p18). AZDecrypt finds a quite good solution without transposition solver. A random hit has provided enough material for parts of the plain text.
Take Magic Square again and apply UPC-2. Then, instead of untranspose p18, untranspose diagonally.
Direction:
AZDecrypt finds a better solution. Its not the correct solution, but it matches way better, that’s all.
I’m just wondering if it is possible to find references to an original "matrix" or something similar by moving individual rows and columns. But how? A Hillclimber and Bi-/Trigram Count will probably lead to a lot of false positives.
One more point: We usually assume a "linear transposition". I can’t think of any other term for it. I explain it with examples: The 2d-period transposition shown in your sample matrix is linear, as it can be performed strictly from beginning to end. However, if we say that the reading rule, for example, starts again from the beginning of the lower half or is even changed there, then it is no longer linear. This may still produce a P19 peak. But if untransposed linear, exactly what you described above happens: it diverges. The same applies if e. g. the first half is transposed forward, the second half is transposed backward with the 2d-period-transposition. Bigramms can occur over the whole cipher. Perhaps our mistake is to search too linearly. I know that AZDecrypt can solve ciphers consisting of several parts with different transposition. However, this also applies again only to linearly transposed parts.
I hope this isn’t just gibberish I’m writing here.
Translated with http://www.DeepL.com/Translator
Okay, I’m afraid this is going to be a textwall…
It would indeed be very interesting to know why this Magic Square appears in the FBI files and what the background is. Is there any way to ask the guys directly? Will one of them remember anything after all these years? People are probably all retired anyway. I can try to find out something about the variation of the Magic Square.
We know who made it but since the person is still alive I became uncomfortable with the POI thread and had it removed by morf13. I will just say that it is not Gareth Penn as I assume doranchak and glurk believed. If you can find something out about the variation it would be awesome.
You take a plain text and transpose it with your "simple example matrix". Let’s just say, just for fun, we can’t solve it after that and then take measurements. At some point we come across P19 and get many bigramms. However, the encryption cannot be solved because "untranspose P19" only finds partial correlations. One could say that P19 is "related" to the matrix, but it is not the solution. After a while we find out that period column order 2 + P18 results in even more bigramms. Unfortunately, this does not lead to a solution either. However, the peak can be explained by a better hit rate of the correct following characters. The correlation is better. So you are saying that the "special bigram peaks" are all indications of the actual transposition and we approach the final solution. Is that summarized correctly?
Yes, well understood.
If so, some of my observations, which I thought to be coincidences, are explained by your idea. (Maybe they are coincidences anyway). To make the examples easier to explain, I’m assuming for fun that z340 was transposed with your "simple example matrix" and we just don’t know it.
Okay cool. Yes, they may be.
PS: I will replace "untranspose perdiod column order" with "UPC", which is shorter.
If z340 is resized to 20×17 and then diagonal 1 untransposed, you get a lot of bigram repeats. No wonder, it’s just a disguised P19, which results in a slope of 261 in relation to the matrix. maybe we’re not closer to the solution, but it may simply match more characters of the original sequence.
"Untranspose P18" and "Untranspose Diagonal" are very similar, you can already see that in a purely visual way. No surprise, but a nice example of how different transpositions can point to the original transposition (or the wrong one).
I am glad that you are using slope as a measure of goodness!
If I shift columns 2 and 4 one character down on z340, I get 42 bigram and 4 trigrams on P19, I know that the matrix you show is only an example, but it fits by random here. Take columns 2 and 4 of your matrix and shift them down by one. The slope increases from 263 to 265 according to untransposed P19 and the first uninterrupted line goes from 1 to 11.
You are shifiting individual columns. I have never attempted that and only shift the cipher by its entirety by columns and/or rows.
Let’s take this game a little further:
Shift Row 3 to the right by one and columns 2 and columns 4 to the bottom by one: 48 bigram, 5 trigrams! Coincidence? Maybe! But if you run the result with AZDecrypt’s transposition solver, you get a lot of results with a score of 21100 and more.
Is this on the 340 now? I guess. 21100+ is certainly not bad but it is hard to say wether you have something or not. Bigrams tend to increase AZdecrypt score. Try to find peaks of the PC-cycles stat, it means that substitution follows the cycles, around 2000 might be a hit.
Maybe we can find a partial solve by such experiments and find the correct solution in a second step (that is what you are suggesting, right?)
Perhaps, but I feel we should have found it by now then.
Another example: Based on your matrix: UPC 2, then untransposed "diagonal 3" (AZDecrypt) the slope rises to 315. P18 is in principle diagonal 3, only the latter simply matches better.
This is interesting, too:
Take your Magic Square and complete number 4 of your list at the top of the thread (UPC 2 + untranspose p18). AZDecrypt finds a quite good solution without transposition solver. A random hit has provided enough material for parts of the plain text.Take Magic Square again and apply UPC-2. Then, instead of untranspose p18, untranspose diagonally.
Direction:AZDecrypt finds a better solution. Its not the correct solution, but it matches way better, that’s all.
Yes, the examples I have provided are solvable and it seems odd that the 340 then does not solve at all.
I’m just wondering if it is possible to find references to an original "matrix" or something similar by moving individual rows and columns. But how? A Hillclimber and Bi-/Trigram Count will probably lead to a lot of false positives.
Hard problem. I have no energy for it now, perhaps you have.
One more point: We usually assume a "linear transposition". I can’t think of any other term for it. I explain it with examples: The 2d-period transposition shown in your sample matrix is linear, as it can be performed strictly from beginning to end. However, if we say that the reading rule, for example, starts again from the beginning of the lower half or is even changed there, then it is no longer linear. This may still produce a P19 peak. But if untransposed linear, exactly what you described above happens: it diverges. The same applies if e. g. the first half is transposed forward, the second half is transposed backward with the 2d-period-transposition. Bigramms can occur over the whole cipher. Perhaps our mistake is to search too linearly. I know that AZDecrypt can solve ciphers consisting of several parts with different transposition. However, this also applies again only to linearly transposed parts.
Could be classified as multiple transcription rectangles in the classical cryptography name space. Before you assume it, make sure that AZdecrypt cannot solve it. If so we can take a look at it and possibly add another operation to the transposition solver to compensate for it.
IDIC.
If you can find something out about the variation it would be awesome.
I’ll do some research. Since you probably have already done this in English/Belgium language, I’ll give it a try in the German-speaking countries.
Is this on the 340 now? I guess. 21100+ is certainly not bad but it is hard to say wether you have something or not. Bigrams tend to increase AZdecrypt score. Try to find peaks of the PC-cycles stat, it means that substitution follows the cycles, around 2000 might be a hit.
Yes, that’s with z340. I get scores up to 21300. I took your advice and looked at the PC-cycle stats of the results with >20900 points, the highest value was 613, but I’m surprised that you’re talking about 2000. Even with z408, this value doesn’t go above 518, so I transposed the first 340 characters of z408 diagonally for testing and then sent them through the transposition solver. One of the first attempts had a score of 20286 and PC-cycles 755, a better solution had a score of 23809, but the PC-cycles were only 518, I don’t quite understand the connection yet.
Hard problem. I have no energy for it now, perhaps you have.
I know this very well, even if from other situationsI Hope you don’t mind if I ask you a few questions from time to time. At the moment I have a lot of =)
Could be classified as multiple transcription rectangles in the classical cryptography name space. Before you assume it, make sure that AZdecrypt cannot solve it. If so we can take a look at it and possibly add another operation to the transposition solver to compensate for it.
Not quite what I meant. Multiple transcription rectangles can be solved if each one is "linear" in itself. A typical non-linear transposition is a way/patch transposition or any other pattern.
IDIC – That’s exactly what it is!
Yes, that’s with z340. I get scores up to 21300. I took your advice and looked at the PC-cycle stats of the results with >20900 points, the highest value was 613, but I’m surprised that you’re talking about 2000. Even with z408, this value doesn’t go above 518, so I transposed the first 340 characters of z408 diagonally for testing and then sent them through the transposition solver. One of the first attempts had a score of 20286 and PC-cycles 755, a better solution had a score of 23809, but the PC-cycles were only 518, I don’t quite understand the connection yet.
That is because you transposed the 408 after encoding. If that is assumed then go to options, solver and set (Substitution + transposition) PC-cycles, use untransposed texts to 0.
PC-cycles stands for "plaintext to ciphertext cycles" and measures how well the substitution that AZdecrypt found lines up with the cycles.
Not quite what I meant. Multiple transcription rectangles can be solved if each one is "linear" in itself. A typical non-linear transposition is a way/patch transposition or any other pattern.
I think that your non-linear transposition can be defined with multiple transcription rectangles nonetheless.
Hey Jarl and Largo,
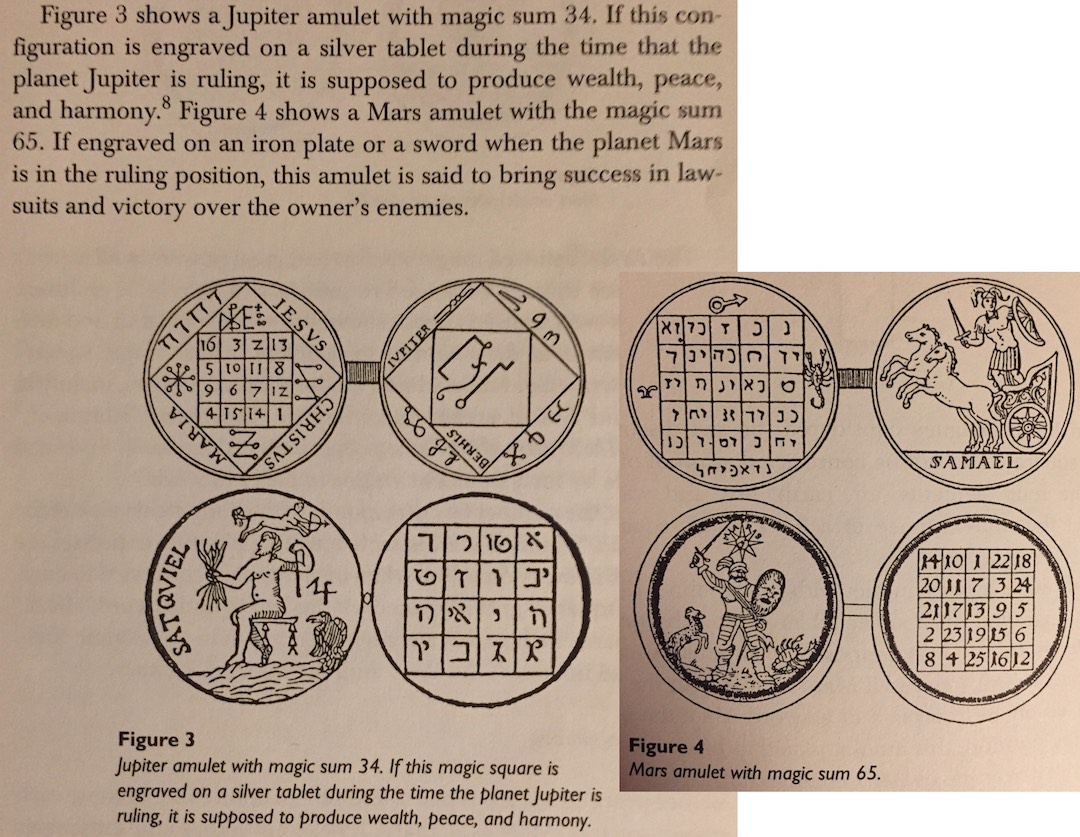
I’ve mostly been lurking working on some other cipher stuff but realized I might have some info for Magic Squares. I while ago off-list I had mentioned to Jarl I found a cool book on Magic Squares (MS) at a used book store but was unaware there was a possible MS "out there" relating to the Zodiac case. If I had known or thought there could be some relevance to Z, I would have tossed out some info on it. The book is called "The Zen of Magic Squares, Circles, and Stars" by Clifford A. Pickover. He has written other books on the subject and it contains a very comprehensive bibliography- perhaps too much to even start to make sense of the 340 in a MS format.
But a couple interesting things that might want to be considered. An interesting concept is the N-Queens problem- put N Queens on a chessboard sized N X N so none can attack each other. There is a simple formula given a known MS to recalculate the value in that MS (simply put the remainder when you divide the MS # by the mod size (N here). All that is really irrelevant since we don’t know what the cipher says, but in the end, the N-Queens solution basically has the N number of Queens placed on the board at "Knight’s move" type positioning. I can scan in a couple examples if it seems helpful, but it makes me wonder if that would then make the Queen’s positions nulls if that was in fact the case.
There is also an N-Super Queens problem where the Queens are placed on a toroidal board- I am a bit unclear but will try to pull its citation. It appears to commonly be a cylinder shape for a chess board, or can even make the chess board any dimension rectangularly (not just square).
Off of Queens now, there are many paths then through the square that can be taken- Knight’s tours are very common, Kings, Rooks,etc. with the only requirement being you hit each position once and end up back where you started. There are MS’s inside of MS’s, there is a prime number MS when using 1-25, it works out to be a Swastika, other shapes for the "MS" like pyramids, crosses, diamonds, and even cubic and other 3-D examples. And of course, from the book’t title- circles and stars. Oh, and also Magic Word squares…
I can tell you it is alot to take in, but it seems to me it leaves many more questions of why Z would use a MS (**any info on the MS from the FBI files would be appreciated- I’ve found its image but know nothing about it or who/why was suspected or eliminated as having made it).
Also, given so much of this can resolve around Chess and/or certainly a higher level of mathematical understanding to generate a MS then Z is expected to have, it would seem to me this could change alot about who does make a good POI.
-marie
The problem when solved will be simple– Kettering
Hi marie
Thank you for pointing out the book. It is really amazing that there is so much reading matter to magic squares. However, I also believe that there are many ways to connect z340 with it. Therefore, I follow the approach of looking for the "simple" possibilities. I just can’t imagine that Zodiac used complex mathematical gimmicks to create z340. IF it is a 2D-transposition and this has something to do with an MS, then probably on a much simpler level. In this case, however, I agree with Jarlve that AZDecrypt should have found a solution long ago. But here too, there are some possible causes: AZDecrypt can solve transpositions, deal with nulls, consider additional plain text characters (e. g. numbers, punctuation marks)… but when these things are combined, the automatic search is difficult. Maybe we already have the right transposition, but there is another hurdle. However, Zodiac may also have used a 2D transposition that results in a cipher so scrambled that AZDecrypt fails. Who knows?
In any case, I will be careful not to adopt a too complex transposition. It just doesn’t fit in the picture.
I found the following link a few days ago (scroll down to the end of the page):
https://pavlopoulos.wordpress.com/tag/m … -kishnawi/
The rule is very simple and generates exactly the same MS from the FBI files. I have included this kind of transition in my tools and have done many tests (details in a few days). I haven’t noticed anything exciting so far. The only interesting thing is the behaviour of the + signs. Depending on the starting point of the untransposition and the rule variants, it can happen that lots of the + characters bundle in a small region of the cipher. This reminds me of what you wrote (swastika/pyramid/diamond shape etc). When I first saw z340, I suspected that the many + signs might form a pattern after correct untransposition. In some other threads I wrote a little bit about it. Maybe a crosshair?
Jarlve:
The 21×21 MS has a P19 spike when flipped or mirrored. It is therefore not necessary to perform a transposition. If you apply the rule shown in the link to 17×20 and then flipping/mirroring it, you have P19, so you can simply mirror z340 and untranspose with the rule. This results in about 37 bigram and 4 trigrams (depending on the starting position and the variants of the rule).
I still have a some ideas, but unfortunately not so much time. So it may take some time until I can provide more details.
Translated with http://www.DeepL.com/Translator
Hi Largo!
First, I want to say I have used your Peek-a-Boo program and its really fun and helpful for many things. I also use Jarl’s. I am amazed at the programming that goes into so much of this so thank you both! (I stumble through a few perl scripts for a theory I have been working on proof of concept for off and on.)
And for my own personal feeling, I am not convinced the 340 is homophonic. I don’t rule anything out until I have proof so I try to read and learn from others on the cipher pages, and have read many cipher books. I am lucky to live near an academic library that has cipher books dating back easily from the 1800’s to the present so I am aware of many simple methods that can be very difficult to decipher yet very simple to encipher.
Thank you for pointing out the book. It is really amazing that there is so much reading matter to magic squares. However, I also believe that there are many ways to connect z340 with it. Therefore, I follow the approach of looking for the "simple" possibilities. I just can’t imagine that Zodiac used complex mathematical gimmicks to create z340. IF it is a 2D-transposition and this has something to do with an MS, then probably on a much simpler level. In this case, however, I agree with Jarlve that AZDecrypt should have found a solution long ago. But here too, there are some possible causes: AZDecrypt can solve transpositions, deal with nulls, consider additional plain text characters (e. g. numbers, punctuation marks)… but when these things are combined, the automatic search is difficult. Maybe we already have the right transposition, but there is another hurdle. However, Zodiac may also have used a 2D transposition that results in a cipher so scrambled that AZDecrypt fails. Who knows? In any case, I will be careful not to adopt a too complex transposition. It just doesn’t fit in the picture.
I agree and disagree. We all assume Z wasn’t intelligent when we really have no idea. Spelling errors have been found not to correlate with IQ, or could have been done intentionally to make us think he wasn’t educated.
Further, the statistics that are used to determine its a homophonic cipher would be highly disturbed given too much transposition. So I do appreciate simplicity. I also am not sure biasing a transposition scheme to increase statistics like bigram number is right either as it is forcing what "we" think is correct. But I am happy to be corrected on this if I am wrong or missing something.
I found the following link a few days ago (scroll down to the end of the page):
https://pavlopoulos.wordpress.com/tag/m … -kishnawi/The rule is very simple and generates exactly the same MS from the FBI files. I have included this kind of transition in my tools and have done many tests (details in a few days). I haven’t noticed anything exciting so far. The only interesting thing is the behaviour of the + signs. Depending on the starting point of the untransposition and the rule variants, it can happen that lots of the + characters bundle in a small region of the cipher. This reminds me of what you wrote (swastika/pyramid/diamond shape etc). When I first saw z340, I suspected that the many + signs might form a pattern after correct untransposition. In some other threads I wrote a little bit about it. Maybe a crosshair?
The book I have has many ways to generate simple to complex MS, and I did play with the FBI one- do you know anything else about it? It seems to be out there that it exists, but not from where.
A transposition scheme to generate something interesting (I have a friend who has connected the symbols with dots and found interesting images- Z does tell us to "connect the dots" in one of his letters) especially with those pesky pluses is a cool idea.
I just try to add my 2 cents when I see an idea like the Magic Square (I do love mathematics) in hopes of adding to the discussion productively, and get people to think about something they have not- we all see the world differently. And I expect none the less from anyone commenting to me. But I do believe, as in my signature below, "the problem when solved will be simple" or at least seem that way!
And just to add some fun Astrology/Zodiac imagery to the whole MS concept, from the book I cited previously. Who knows what inspired Z to become the Zodiac:
-marie
The problem when solved will be simple– Kettering
We all assume Z wasn’t intelligent when we really have no idea.
My opinion is quite the opposite and find myself in the Sherwood Morrill camp on that one. I cannot imagine the Zodiac, whose indentity that has eluded us for almost 50 years now, as unintelligent.
And thank you marie for using my program!