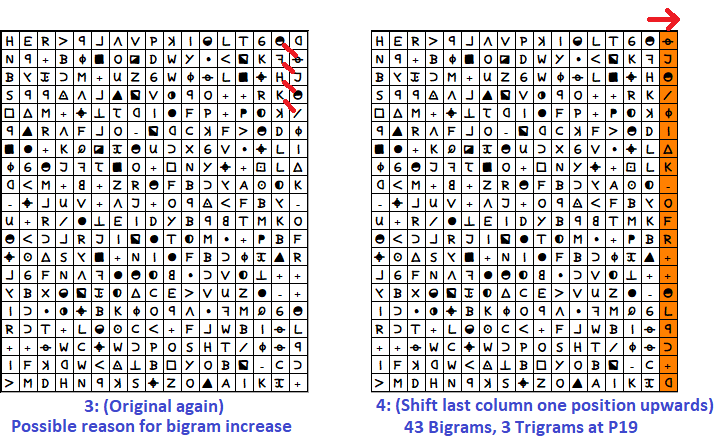
Some of my current experiments deal with very simple shifting operations. I have been using some of the known manipulations that lead to special bigram peaks as a basis. For example the one where 45 bigrams and 4 trigrams on P19 are achieved by simply moving the cipher one letter to the right. How does such a thing come about and how can it be represented in another way?
Figure 1 Shows the original z340. Figure 2 shows how z340 was shifted one position to the right. Important is the right edge at which the line break takes place. As you can see, the order of the letters in Figure 1 and Figure 2 are identical except for this line break. So one can assume that the increase of the bigrams is caused by this wrap.
A small example: In Figure 1, the last character of the first row is an inverted D, the first character of the second row is an N. Due to the shift in Figure 2, the last character of the first row is the half-filled circle and the first character of the second column is the crossed-out circle. Otherwise, the two rows are identical. This applies to all rows up to the end of the cipher. This means that the bigram increase is obviously only caused by this small area.
In figure 3 you can see the original z340 again. This time the red lines show the connections, which are raised by the shift in figure 2. A very simple diagonal. How can this be achieved in an alternative way? You simply shift the last column up by one. Figure 4 shows what is meant. Now the symbols concerned are again next to each other, whereby the largest part of the cipher remains unchanged in its order. And what does this result in? 43 bigrams and 3 trigrams on P19.
As you can see, the increase of the nGrams can be traced back to a simple manipulation of a small area of the cipher.
How helpful is that? To be honest, I don’t know it yet. Could this be a starting point with which one can begin to find out a possible transposition rule? Unfortunately, a high nGram count is not necessarily the only sign that you are getting closer to the solution. As doranchak explained in his talk, very high nGram counts can be achieved by manipulating the cipher sufficiently. This is logical, because with enough steps you can tinker almost everything out of the cipher. But if a significant increase can already be achieved by simple manipulations, this is a starting point in my opinion.
What do you think? Do I miss something, do I hunt unicorns, or could we approach the bottom of the Special Bigram Peaks in such a way?
Translated with http://www.DeepL.com/Translator
How does such a thing come about and how can it be represented in another way?
My take on this – per the thread – is that these "special bigram peaks" could be an indication of a 2-dimensional period 19 transposition rather than a 1-dimensional one. So that is how it can come about and I have documented that rather well. Why do you want to represent it in another way?
What do you think? Do I miss something, do I hunt unicorns, or could we approach the bottom of the Special Bigram Peaks in such a way?
What is your point besides the stuff that was already apparent from this thread and previous work?
My take on this – per the thread – is that these "special bigram peaks" could be an indication of a 2-dimensional period 19 transposition rather than a 1-dimensional one. So that is how it can come about and I have documented that rather well. Why do you want to represent it in another way?
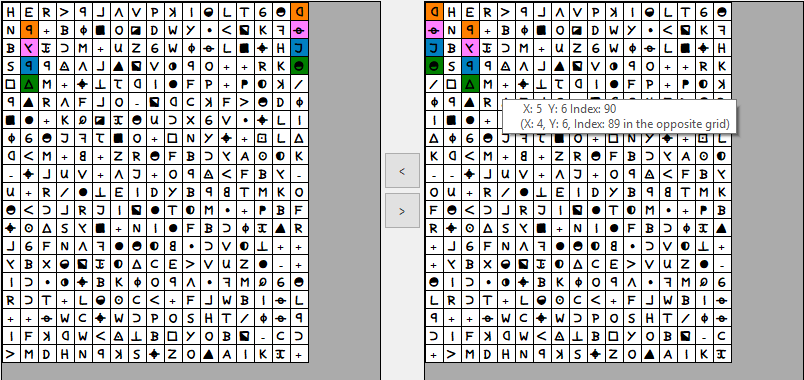
I don’t want to work against the intention of this thread. Rather, I would like to examine some of the already made observations from different sides. In the first posting of this thread you described for example the operation "2. Offset column order 1 + untranspose period 19: 45 bigrams". Exactly these I have examined in my posting to find out how such an increase can come about (shift the cipher 1 to the right is the same like offset column order 1". Whether there is a 1D or 2D transposition underneath is independent of this. Understanding the causes more precisely helps in both cases, doesn’t it? My images should show that certain phenomena can be explained differently. In this particular case, the point was that an offset column order can have similar effects to shifting columns up/down. I thought that looking at the relationships optically could help.
It is a bit like understanding a calculation method. If you only know the result, it is impossible to determine the calculation method. For example, how do you get the number 36? By 4*9, 3*12 or 6*6, if you only consider multiplications. But it also works with 30+6, 40-4 or 72/2. But I can understand if my ideas are too out of line with the actual thread. In this case I can open a separate thread.
What is your point besides the stuff that was already apparent from this thread and previous work?
As I said before: Looking at things from different perspectives. This thread seemed to me to be the most appropriate and I thought it would be unnecessary to open a new one. If I’ve posted something that someone else has already described, it’s certainly not intentional. There are so many threads and posts now that it is hard to remember what has already been discussed and what has not. At least to me.
Translated with http://www.DeepL.com/Translator
I believe that these may be connected to a specific type of period 19 transposition. Likely some sort of 2-dimensional period in a grid. Significance wise, if we consider many randomizations of the 340 and find the highest bigram result in the set "period 1 to 170" for each randomization, the bigram peak of 37 at period 19 has a 3.56 sigma (standard deviations). The reason why I did not include periods over 170 (half of 340) is that these are coarse rearrangements of period 1. A 7.00 sigma was recorded for the bigram peak of 45 for offset column order 1 + untranspose period 19 by finding the highest bigram result in the set "offset column order 0 to 16 times period 1 to 170" for each randomization.
I reran these tests, the results were the same but also recorded the odds. It just blew my mind again.
– While taking the highest result from period 1 to 170, a bigram peak of 37 or better occurs 1 in 210 randomizations.
– While taking the highest result from offset column order 0 to 16 + period 1 to 170, a bigram peak of 45 or better occurs 1 in 100000 randomizations.
Period 1 to 170: ---------------- Combinations processed: 1000000/1000000 Measurements: - Mean: 30.630392 - Variance: 3.194237926332565 - Standard deviation: 1.787243107787121 - Count equal/over 37: 4914 - Sigma of 37: 3.563929256320672 - Sigma of 25: -3.15032240184229 - Sigma of 45: 8.040097028429313 - Lowest: 25 (Randomize(71118)) - Highest: 45 (Randomize(845554)) Offset column order 0 to 16 + period 1 to 170: ---------------------------------------------- Combinations processed: 5000000/5000000 Measurements: - Mean: 33.826494 - Variance: 2.545902067836069 - Standard deviation: 1.59558831401965 - Count equal/over 45: 33 - Sigma of 45: 7.002749958635256 - Sigma of 29: -3.024899316190754 - Sigma of 48: 8.882934197665133 - Lowest: 29 (Randomize(13055)) - Highest: 48 (Randomize(45822))
Odds Even ROWS . then COLUMN shift up one gives one of the better bi gram results.. simplistic in its means. .. but a poor solve. may be the first line is
(DON HARDENS IDEADAN)
DONCARDONSIDEEDAN
DSPRINTIMINOREAND
ONTHEATTHESHEILLB
EATINSCHEADLETSTO
ADGUNSTLORMANYMAS
LYSHEAURIESINCECA
NIEHSHHEDTHEETORS
BYIFITTAGOFLANETH
RENATOITSAMCAPINE
ACULAWARBEANDOORE
RHASFAIRSOUNGHAMO
UNTLERONTRACIERAL
LYANDHPPYHCROSSTH
ENTEROLERICELANDP
URSELEEEALTINIONT
INDEDOUTANTTOFANE
THBYYESINTHTRFEIN
OUDIENDGUSSTOBEAT
ASOURSAWARMATIOND
RSTOOLAYEDDEDATRI
AZdecrypt multigrams stats for:
——————————————————–
Bigrams: 41
– Normalized: 0.1547169811320755
Bigram ioc: 98
– Normalized: 0.0008552826796529996
Ngrams: 49
Asymmetry: 2446
I believe that these may be connected to a specific type of period 19 transposition. Likely some sort of 2-dimensional period in a grid. Significance wise, if we consider many randomizations of the 340 and find the highest bigram result in the set "period 1 to 170" for each randomization, the bigram peak of 37 at period 19 has a 3.56 sigma (standard deviations). The reason why I did not include periods over 170 (half of 340) is that these are coarse rearrangements of period 1. A 7.00 sigma was recorded for the bigram peak of 45 for offset column order 1 + untranspose period 19 by finding the highest bigram result in the set "offset column order 0 to 16 times period 1 to 170" for each randomization.
I reran these tests, the results were the same but also recorded the odds. It just blew my mind again.
– While taking the highest result from period 1 to 170, a bigram peak of 37 or better occurs 1 in 210 randomizations.
– While taking the highest result from offset column order 0 to 16 + period 1 to 170, a bigram peak of 45 or better occurs 1 in 100000 randomizations.
The sigma’s I mentioned in this thread are incorrect as the distribution is not symmetrical. I updated the odds, the jump from 37 to 45 with the column offset is significant.
Happy new year!
This is once again one of those coincidences…I couldn’t sleep well a few days ago and promptly z340 haunted my head. (Not a good thing, I know). And as chance would have it, it was exactly about the column offset and the associated increase of the Bigram peaks.
I know…we had already discussed that a possible 2D transposition could be the reason that shifts of the cipher bring more "hits" of the original order and thus more bigrams. However, I wanted to know which letters play a role for the additional 8 bigrams that are created by moving the cipher one column to the left. I noticed that on its right edge many P19 pairs (pairs, not bigrams!) are lost. Since I can only describe this badly, here is a picture:
On the left the original z340, on the right moved by one column. As you can see, the P19 pairs at the edge now become P2 pairs. So that it doesn’t get too colorful, I only marked four pairs.
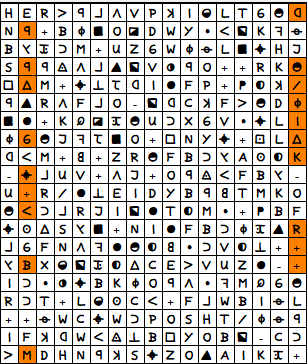
For the left edge of the cipher, the opposite applies. Here, former P2 pairs now become P19 pairs:
While some potential pairs for bigrams on P19 are lost, other potential pairs are added. If you now check which of the letters are involved in bigrams, you will see the following:
So these two columns seem to be really responsible for the additional bigrams. Sorry if it’s just a gimmick again, or if we’ve had it before, but I’m trying to understand visually what’s happening with the column shift. Maybe at some point I’ll discover a pattern or context.
Since there are only three pictures per posting, I will post the rest immediately afterwards:
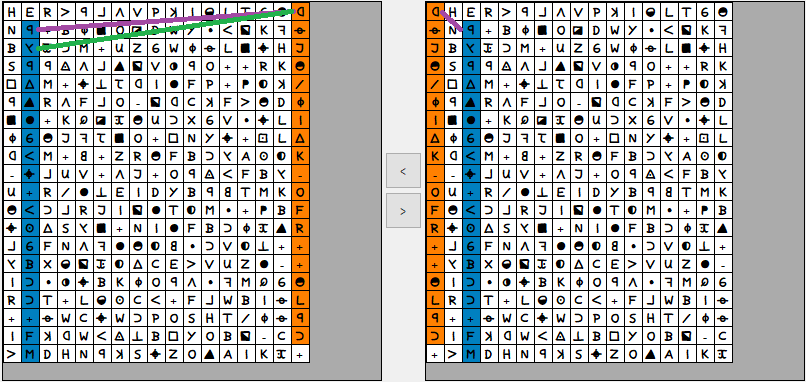
On this image you can see again what the shifting of the cipher to the left causes. In the unmodified z340, a P19 transposition causes the reversed D to be followed by the reversed Y. After the shift the reversed D is followed by the reversed P. Period 19 of the orange column always hits the blue column in both cases, but is shifted by one letter. Sorry that I can’t express myself better here. I’m not only struggling with z340, but also with the fact that I can’t write these confusing thoughts in my native language =)
In my opinion, the just shown picture can be a hint for a special kind of wrap-around. If a 2D transposition or some kind of P19 has been used, then it is exactly this wrap at the edge that could be the reason why we are stuck in a dead end. Again, sorry if this has already been discussed.
Hence my idea: I will try to create some kind of heat map. To do this I move the cipher horizontally and/or vertically and determine the bigrams. Then in the unmodified z340 it is marked which letters are involved. I have no idea if this will lead to anything, but I’ll try =)
Translated with http://www.DeepL.com/Translator
Here are the heatmaps:
z340 unmodified
z340 resized to 20×17
In the upper image you can see z340 unmodified. In the second image z340 was resized to 20×17.
Here the pseudo-code how it works:
for 1 to cipherWidth shift cipher left untranspose P19 determine bigrams mark involved indices in unmodified z340
So the heatmap shows how often which original index leads to bigrams in the tranpositions. Let’s see what can be done with it. However, I’ll do a few more tests before I make any assumptions.
Happy newyear to you too Largo and to everyone else ofcourse!
So these two columns seem to be really responsible for the additional bigrams. Sorry if it’s just a gimmick again, or if we’ve had it before, but I’m trying to understand visually what’s happening with the column shift. Maybe at some point I’ll discover a pattern or context.
Yep, that is indeed what is happening. I think smokie touched on it before. Thanks for the illustrations!
So the heatmap shows how often which original index leads to bigrams in the tranpositions. Let’s see what can be done with it. However, I’ll do a few more tests before I make any assumptions.
Cool idea.
I’ve done some tests with different self-created ciphers. I used transpose P19 and some diagonal transpositions. From these ciphers I generated heat maps as well. I didn’t notice anything that could be used. I think the significance of the heat maps is not very high. Too bad, but it was worth a try.
I believe that these may be connected to a specific type of period 19 transposition. Likely some sort of 2-dimensional period in a grid. Significance wise, if we consider many randomizations of the 340 and find the highest bigram result in the set "period 1 to 170" for each randomization, the bigram peak of 37 at period 19 has a 3.56 sigma (standard deviations). The reason why I did not include periods over 170 (half of 340) is that these are coarse rearrangements of period 1. A 7.00 sigma was recorded for the bigram peak of 45 for offset column order 1 + untranspose period 19 by finding the highest bigram result in the set "offset column order 0 to 16 times period 1 to 170" for each randomization.
I reran these tests, the results were the same but also recorded the odds. It just blew my mind again.
– While taking the highest result from period 1 to 170, a bigram peak of 37 or better occurs 1 in 210 randomizations.
– While taking the highest result from offset column order 0 to 16 + period 1 to 170, a bigram peak of 45 or better occurs 1 in 100000 randomizations.The sigma’s I mentioned in this thread are incorrect as the distribution is not symmetrical. I updated the odds, the jump from 37 to 45 with the column offset is significant.
I never really calculated the odds from jumping to 37 to 45, with jump I meant increase.
Here is a new test I did:
1) Generate a random 340 shuffle that has 37 bigram repeats at period 19.
2) Period 1 offset column order from 0 to 16 and find the highest bigram repeat peak at period 19 as a single result. It must be 45 or higher.
3) Repeat 10,000 times.
The odds are 2 in 10,000. I am surprised. It is very significant. Multiplying the odds of period 19 and the jump from 37 to 45 results in something like 1 in 1,000,000 (210 * 5000).
For the uninitiated here is an example of a "offset column order" operation:
Offset column order 1: ---------------------- - Simply shift all rows to the right by one position. Before: After: ----------------- ----------------- HER>pl^VPk|1LTG2d dHER>pl^VPk|1LTG2 Np+B(#O%DWY.<*Kf) )Np+B(#O%DWY.<*Kf By:cM+UZGW()L#zHJ JBy:cM+UZGW()L#zH Spp7^l8*V3pO++RK2 2Spp7^l8*V3pO++RK _9M+ztjd|5FP+&4k/ /_9M+ztjd|5FP+&4k p8R^FlO-*dCkF>2D( (p8R^FlO-*dCkF>2D #5+Kq%;2UcXGV.zL| |#5+Kq%;2UcXGV.zL (G2Jfj#O+_NYz+@L9 9(G2Jfj#O+_NYz+@L d<M+b+ZR2FBcyA64K Kd<M+b+ZR2FBcyA64 -zlUV+^J+Op7<FBy- --zlUV+^J+Op7<FBy U+R/5tE|DYBpbTMKO OU+R/5tE|DYBpbTMK 2<clRJ|*5T4M.+&BF F2<clRJ|*5T4M.+&B z69Sy#+N|5FBc(;8R Rz69Sy#+N|5FBc(;8 lGFN^f524b.cV4t++ +lGFN^f524b.cV4t+ yBX1*:49CE>VUZ5-+ +yBX1*:49CE>VUZ5- |c.3zBK(Op^.fMqG2 2|c.3zBK(Op^.fMqG RcT+L16C<+FlWB|)L LRcT+L16C<+FlWB|) ++)WCzWcPOSHT/()p p++)WCzWcPOSHT/() |FkdW<7tB_YOB*-Cc c|FkdW<7tB_YOB*-C >MDHNpkSzZO8A|K;+ +>MDHNpkSzZO8A|K;
Untransposing period 19 in the after example will return 45 bigram repeats.
The 340 appears to be a period 19 cipher but is not solving as one. What’s the problem?
You scrolled the message to the right one space and found a lot more period 19 repeats. If someone made a 19 x 18 scytale message, but when transcribing into a 17 x 20 grid, does the start position at the top affect the number of period 19 repeats? I always assumed that the person would start with the first letter in the message, but maybe starting with another position will affect the number of repeats.
What about period 15?
I have been thinking about it a lot, and still think that this is a transposition or scytale message. But it could be period 18 or period 14 with a lot of nulls at regular intervals or something like that. I think that he could have had a cylinder, and wrote a word or couple of words a few times in a pattern, then inscribed the message vertically on the cylinder and then transcribed the whole thing into the 17 x 20 grid. The word or couple of words, or whatever they are that he put on the cylinder first before inscribing the message show up as the pivots and other symbols involved with period 16, 32 and 48 unigram repeats. Even the pivot nodes are in them. Those clusters just cannot be ignored.
Consider "nulls" at regular intervals, like a diagonal inscription on the cylinder first before the message was inscribed. There would be three variables to change. The start position, the interval, and the end position. After deleting the nulls, try to untranspose at period 18 or period 14. Perhaps a cylinder 14 spaces in diameter. The nulls inscribed on the interval make period 14 go to period 15, and period 28 go to period 29.
It is a homemade paper and pencil cipher, so I just think that it is something simple like that and we aren’t seeing it for what it is.
EDIT: Five variables. The fourth variable is the number of times the pattern is written and the fifth variable is the spacing of the pattern.
You must have scrolled the columns to the right one space, and tried to solve it. If he made a P19 scytale or transposition message and started the inscription with another position instead of position 1, and there were nulls, but not at regular intervals like we tried so hard at in 2018, would that defeat our ability to solve? In other words, should we consider trying with the program that we have, but with the scrolled message?