If someone made a 19 x 18 scytale message, but when transcribing into a 17 x 20 grid, does the start position at the top affect the number of period 19 repeats? I always assumed that the person would start with the first letter in the message, but maybe starting with another position will affect the number of repeats.
Nevermind I tried it. I inscribed a 20 x 17 scytale message vertical, then transcribed into the 17 x 20 grid, but starting at a different position instead of position 1. Then I untransposed and P20. The message would have solved if encoded. It was just shifted around a little bit.
You scrolled the message to the right one space and found a lot more period 19 repeats.
Let me put it in other words.
We could assume that the 37 bigram repeats at period 19 is an outlier. And then find that the operation "offset column order 1" as described in my previous post increases period 19 bigrams from 37 to 45. Is that increase from 37 to 45 something we would expect to see from an outlier? No, per the test I described in my previous post this happens only 2 times in 10,000 samples.
What about period 15?
It decreases. Highest other than 41 is 40.
If he made a P19 scytale or transposition message and started the inscription with another position instead of position 1, and there were nulls, but not at regular intervals like we tried so hard at in 2018, would that defeat our ability to solve? In other words, should we consider trying with the program that we have, but with the scrolled message?
I am not sure. But before I ever run that test again I want a new computer. :’)
We could assume that the 37 bigram repeats at period 19 is an outlier. And then find that the operation "offset column order 1" as described in my previous post increases period 19 bigrams from 37 to 45. Is that increase from 37 to 45 something we would expect to see from an outlier? No, per the test I described in my previous post this happens only 2 times in 10,000 samples.
This test is really interesting. If p19 is actually an outlier, then the increase from 37 to 45 would really be an enormous coincidence. This reminds me of one of my tests that leads to 48 bigrams and 8 trigrams:
viewtopic.php?p=55478#p55478
viewtopic.php?p=55478#p55529
By comparatively few transposition operations one obtains enormously high nGram values. What makes me wonder is that the number of nGrams is too high for an average text with 340 characters and 63 homophones. If we actually found something with transpose x + p19, then the plaintext must be very repetitive. Alternatively, it could also be a simple pattern that was transposed in a way unknown to us so far and is no longer recognizable as such. The pivots and the clusters on the outside could be leftovers.
I know that you think this is rather unlikely. But I can’t explain the high nGram numbers any other way. Repeating text or hoax/pattern.
A little request:
You had posted a piece of code a long time ago, with which you could count the number of bigrams in a text very performant. Unfortunately I can’t find it in the forum anymore. Can you please post this again? My code gives me all the desired nGrams, but unfortunately not at high speed =)
It is a homemade paper and pencil cipher, so I just think that it is something simple like that and we aren’t seeing it for what it is.
I agree 100%. I still believe it’s absolutely possible that a very simple – but as yet unthought – thing is keeping us from solving z340.
You scrolled the message to the right one space and found a lot more period 19 repeats. If someone made a 19 x 18 scytale message, but when transcribing into a 17 x 20 grid, does the start position at the top affect the number of period 19 repeats? I always assumed that the person would start with the first letter in the message, but maybe starting with another position will affect the number of repeats.
But you have to keep in mind that scrolling the whole cipher does not only shift the start position. At the end of each line there is a completely different wrap. See: viewtopic.php?f=81&t=3591&start=20#p67042
Translated with http://www.DeepL.com/Translator (free version)
Let me put it in other words.
We could assume that the 37 bigram repeats at period 19 is an outlier. And then find that the operation "offset column order 1" as described in my previous post increases period 19 bigrams from 37 to 45. Is that increase from 37 to 45 something we would expect to see from an outlier? No, per the test I described in my previous post this happens only 2 times in 10,000 samples.
Very interesting, Jarlve!
I would also put it another way: You have possibly demonstrated that untransposing at period 19 is an incomplete or inadequate reversal of the steps that were done to the enciphered message.
I have run through hundreds of simplistic double transposition methods. eg cut columns into strips arrange odds even, write out result and then cut into rows and arrange odds even. write out result and commit to a substitution method. (and of course left to right or top to bottom could come into play. so in fact it would (or could) be three or four cipher methods used.
These processes are simple and fairly quick and all done with paper, pencil and scissors. (I do use a spreadsheet but keep simplicity in mind)
The simplest way to bring the high period 19 results together is columnar odds evens and then raise each column up one space.
but alas I am still failing even though I know of thousands of ways it wont solve. I think it would be easier to invent the ![]()
This test is really interesting. If p19 is actually an outlier, then the increase from 37 to 45 would really be an enormous coincidence.
Yes.
This reminds me of one of my tests that leads to 48 bigrams and 8 trigrams: …
By comparatively few transposition operations one obtains enormously high nGram values. What makes me wonder is that the number of nGrams is too high for an average text with 340 characters and 63 homophones.
Yes, I believe it is similar. The number of n-gram repeats is not too high since the first 340 characters of the Z408 have 46 bigram repeats and 7 trigram repeats (at a lower IOC than the Z340).
A little request:
You had posted a piece of code a long time ago, with which you could count the number of bigrams in a text very performant. Unfortunately I can’t find it in the forum anymore. Can you please post this again? My code gives me all the desired nGrams, but unfortunately not at high speed =)
function m_fastbigrams(cip()as long,byval l as integer,byval s as integer)as integer 'cip()=cipher array numbered by appearance 'l=cipher length 's=cipher symbols dim as short id(s,s),i,reps for i=1 to l-1 if id(cip(i),cip(i+1))=0 then id(cip(i),cip(i+1))=1 else reps+=1 end if next i return reps end function
This could be faster still by making the id() array static and the use of a counter:
c+=1 for i=1 to l-1 if id(cip(i),cip(i+1))<c then id(cip(i),cip(i+1))=c else reps+=1 end if next i
Very interesting, Jarlve!
I would also put it another way: You have possibly demonstrated that untransposing at period 19 is an incomplete or inadequate reversal of the steps that were done to the enciphered message.
Yes. That is also the general theme of this thread. Though I am still skeptic with all the things we’ve tried…
The simplest way to bring the high period 19 results together is columnar odds evens and then raise each column up one space.
Do you have a transcription?
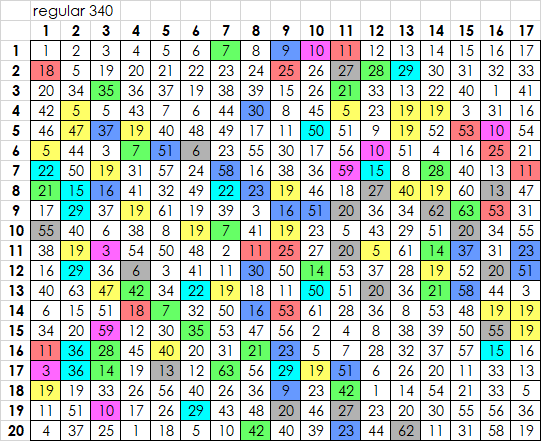
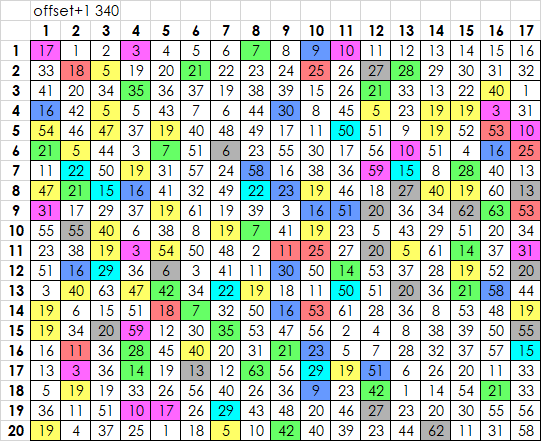
16
14 32
12 30 1
10 28 22 31
8 26 33 19 10
6 24 26 23 52 25
4 22 39 45 9 4 13
2 20 19 30 50 10 28 13
17 5 36 6 17 17 15 19 53
15 33 34 43 48 55 36 27 62 34
13 31 41 5 19 6 16 46 36 51 31
11 29 40 16 47 7 24 23 51 43 14 20
9 27 13 3 54 44 31 49 3 23 5 19 44
7 25 21 19 53 21 50 41 19 41 27 37 21 19
5 23 15 5 19 16 11 15 19 19 11 14 20 53 55
3 21 38 8 51 51 40 47 29 38 48 30 50 36 39 15
1 19 37 44 11 56 8 60 31 40 54 41 18 61 8 37 33
18 35 7 49 30 59 40 63 55 19 6 22 16 2 28 20 33
20 5 40 23 38 18 34 20 23 29 42 32 47 5 6 54 56
42 37 51 58 19 20 29 37 51 63 18 35 21 19 1 30 58
46 3 57 22 16 5 61 52 3 15 12 20 56 23 23 11
5 19 32 39 19 20 28 58 19 20 45 12 36 46 44
22 16 61 7 25 53 36 48 19 36 19 40 48 39
21 37 8 2 50 51 8 50 16 36 26 29 42
17 6 50 11 11 28 38 57 13 19 17 5
55 3 3 19 53 4 32 11 5 51 1
38 36 34 50 56 7 26 21 36 37
16 47 7 53 23 51 14 55 19
40 51 30 31 29 42 20 31
6 59 40 63 9 27 62
34 28 13 26 20 23
11 14 56 43 40
3 33 26 10
19 10 18
11 25
4
I am glad that you have been persistent about showing this to us. Previously I never put much stock in it because I was preoccupied with other stats and couldn’t think of a simple pencil and paper cipher operation that isn’t just arbitrary that would cause this.
Perhaps a scytale with a circumference of 19. Then, transcribed onto another cylinder with circumference 17 that already had some patterns and stuff that is making it so difficult to solve. Then when made two dimensional, the first column is merely offset by one. That I think would do it. Simple, you still get your high P19 stats, but also a lot of nulls and the column offset phenomenon.
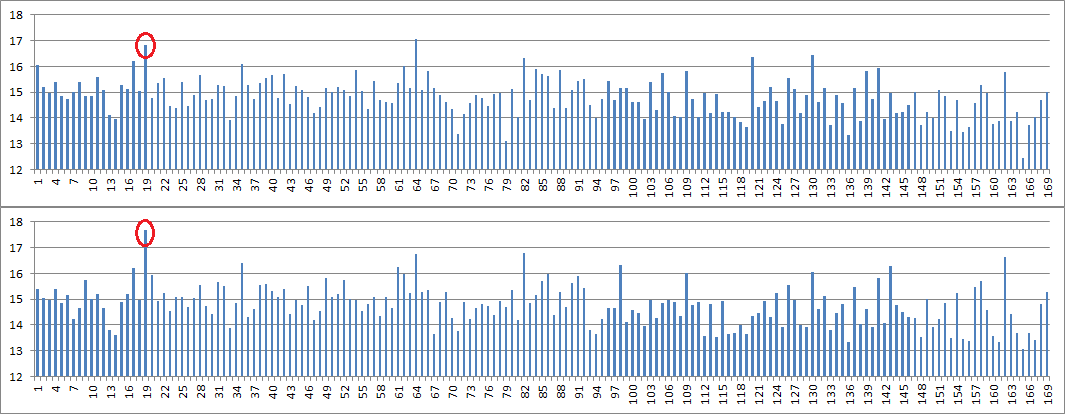
I score my bigrams by symbol frequency, because plaintext bigrams with low frequency letters oftentimes shine through after homophonic encoding. See top chart here, the average bigram score for the 340 P19 is 16.8, with only period 64 slightly higher at 17.1. But on the bottom chart, the average bigram score for the offset+1 340 P19 jumps way up to 17.7 and is by far the tallest spike.
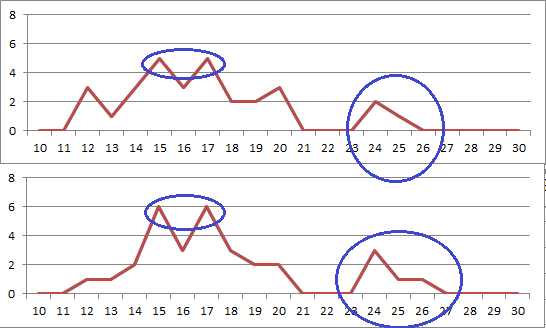
The top chart here shows the distribution of scores for 340 P19, and with the bottom chart offset+1 340 the distribution shifts up and to the right for the highest scoring bigrams.
Thank you for the source code Jarlve!
Bigrams: 41
– Normalized: 0.1547169811320755
Bigram IOC: 98
– Normalized: 0.0008552826796529996
Trigrams: 4
the odds even 1+up column has a great 41 count with 4 trigrams as well..and the first words don cardon …nearly … don harden
Let me put it in other words.
We could assume that the 37 bigram repeats at period 19 is an outlier. And then find that the operation "offset column order 1" as described in my previous post increases period 19 bigrams from 37 to 45. Is that increase from 37 to 45 something we would expect to see from an outlier? No, per the test I described in my previous post this happens only 2 times in 10,000 samples.
I ran a test on the Z340 with AZdecrypt’s simple transposition solver logging the amount of bigram repeats. It goes up to 51 bigram repeats:
Bigram repeats: average plain text to cipher text cycle score (samples) 15: 438 (1) 20: 234 (1) 21: 348.5 (8) 22: 382.1 (20) 23: 339.34 (35) 24: 374.14 (85) 25: 382.98 (276) 26: 384.89 (701) 27: 388.22 (1441) 28: 390.47 (2689) 29: 388.17 (4530) 30: 393.42 (6138) 31: 393.82 (7005) 32: 394.23 (6646) 33: 393.22 (5262) 34: 397.21 (3870) 35: 403.60 (3130) 36: 400.73 (3327) 37: 404.01 (5570) 38: 406.30 (3287) 39: 406.66 (3702) 40: 400.73 (2925) 41: 402.27 (2177) 42: 401.77 (1118) 43: 410.34 (592) 44: 408.61 (522) 45: 398.27 (309) 46: 397.20 (172) 47: 360.68 (50) 48: 361.5 (10) 49: 592.5 (2) 50: 219 (1) 51: 594 (1)
Then I randomized the Z340 to have 37 bigram repeats at period 19:
Oz(U8^pl+L+ORFV4p 9UGBZ|*+|/_(+6S-_ #Ucp<p)Slb+WC+bHz .+ZDWtA5/LOJZVkC4 V+NO)KT1*8BBBPLzU ^B5.|zf)VXd_|c+5^ E/+lYVRKK2W.Mzl:| OJftFAFt2Py4@X;EF OTyCRW(FN2JHzMc2q Nkl6C27OJ-:FR;Dk2 ^<%FYHBG*cR3>9#Bc 1GM|DY(^ETFkp&zcK C<O;(4B++LLMV(dG< +ccO+3lMp-7c&|+c6 .Yb<Z#8pK+HBRR>lt KzpW49BzKdF+O>27+ +BBy|5+-SdR5512Dy *.)T+9Fj#Uf5p*jpq p%yG#->8GM|fdMT.+ NkS+)L|4^*<+(PN2W
Which gave the following table, note that bigram repeats only go up to 45:
Bigram repeats: average plain text to cipher text cycle score (samples) 12: 354 (1) 17: 240 (3) 18: 130 (2) 19: 173.87 (8) 20: 217.85 (20) 21: 230.6 (70) 22: 230.92 (123) 23: 222.24 (257) 24: 227.36 (410) 25: 222.95 (812) 26: 222.07 (1502) 27: 225.08 (2657) 28: 222.29 (4354) 29: 222.03 (5494) 30: 225.57 (5947) 31: 224.01 (5547) 32: 221.64 (4689) 33: 223.05 (4214) 34: 224.18 (5098) 35: 221.52 (7455) 36: 222.55 (4448) 37: 217.74 (5347) 38: 222.60 (9589) 39: 220.64 (4914) 40: 224.49 (2042) 41: 223.22 (461) 42: 218.33 (124) 43: 212.79 (24) 44: 228 (5) 45: 249 (1)
I think it further illustrates what we already knew. The 37 bigram repeats at period 19 in the Z340 are just the tip of the iceberg. And it does not seem to act like a "random" bigram repeat peak (that would occur by chance).
Jarlve’s analysis of chances that a random cipher, having 37 repeating bigrams at period 19, would jump to 45 with a column offset.
Column period 2 combined with linear period 18 produces 44 repeating bigrams (doranchak)
Shift operations combined with periodic untransposition and mirroring leads to 48 bigrams and 8 trigrams. (found by Largo)
What I’ve been asking myself for a long time: what comes out of comparing the bigrams of P19, Shift Horizontal + P19 and my 48 bigrams / 8 trigrams cipher? Which bigrams are identical in all three variants, which ones are missing and which ones have been added? In the first variant we have 37 bigrams, in the second 45 and in the third 48. So you might think that the bigrams found in the "better" cipher are added to the ones of the previous one. Should the bigrams in the three variants differ too much, then this would be quite remarkable. But if they are mostly identical, then one could map their start index in the transposed cipher back to the start index in the original cipher. Possibly one could recognize a pattern and predict where further potential bigrams are hidden.
Has something like this already been done? If not, it will be at the top of my todo list.
A little more clearly here again.
Let’s assume that P19 has the following bigrams (I’ll just show some fictitious bigrams, otherwise it will be too confusing)
P19: +R : 2 times xl : 2 times B- : 2 times !K : 2 times Shift horizontal + P19: +R : 3 times xl : 3 times B- : 2 times !K : 2 times fV : 2 times
In this case the number of "+R" and "xl" bigrams would have increased by one each and the bigram "fV" would have been added. This is what one would expect. Now a contrary example:
P19: +R : 3 times xl : 2 times B- : 2 times !K : 2 times Shift horizontal + P19: +R : 2 times xl : 0 times B- : 0 times !K : 2 times fV : 2 times A# : 3 times gH : 3 times
In this case the shifted cipher would only have half of the bigrams of P19 in common. However, since both ciphers have a significantly high number of bigrams, it would indeed be very surprising if the ciphers did not share most of the bigrams.
Translated with http://www.DeepL.com/Translator (free version)