I’ve been doing some experiments over the last few days. Unfortunately I can’t explain their results at all. Either I overlook a big mistake in my approach, or I found something that could help us.
It is well known that with very simple operations the number of bigrams can be strongly increased. Jarlve has described some of them in this thread:
Another example: If you shift column 17 up by one, you get 43 bigrams and 3 trigrams on P19. This list could be extended at will.
To possibly discover more such things, I wrote a very simple test based on my "Deceptive Periods" test. An array of size 17 is created. Each entry represents a column in z340 and can be either 0 or 1. If the entry is 0, the corresponding column remains unchanged. If the entry is 1, the column is shifted down by one. Such a shift looks like this:
Before: A B C D E After: E A B C D
There are a total of 131073 ways to fill the array. I went through all combinations and checked for periods from 1 to 20, which has the highest ngram count. The results have been added to a list. If the highest ngram count occurred at several periods, all periods were added to the list.
Code:
int currentCombination = 1;
int bestNGramCount = 0;
int maxPeriod = 20;
SortedDictionary<int, int> bestPeriodDistribution = new SortedDictionary<int, int>();
foreach (var c in Toolbox.CombinationsWithRepetion(new int[] { 0, -1 }, 17))
{
Cipher cipherResult = cipherOriginal.ShiftColumnsByList(c.ToArray());
Cipher.PeriodInfos periodInfos = cipherResult.GetBestPeriods(2, maxPeriod);
foreach (var x in periodInfos.bestPeriods)
{
if (bestPeriodDistribution.ContainsKey(x))
{
bestPeriodDistribution[x]++;
}
else
{
bestPeriodDistribution[x] = 1;
}
}
}
Now one could assume that P19 stands out a little in this list and that all other periods have a fairly evenly distributed scoring. But I was wrong about that. Take cover, many numbers to follow:
z340 bigrams
Period 1 -> 26593 <<<-------------- Period 2 -> 4901 Period 3 -> 5132 Period 4 -> 13324 Period 5 -> 18000 Period 6 -> 4367 Period 7 -> 2820 Period 8 -> 1363 Period 9 -> 1051 Period 10 -> 1835 Period 11 -> 7029 Period 12 -> 4857 Period 13 -> 3971 Period 14 -> 429 Period 15 -> 2105 Period 16 -> 21915 <<<-------------- Period 17 -> 269 <<<-------------- Period 18 -> 7406 Period 19 -> 30558 <<<-------------- Period 20 -> 977
As you can see, P19 is the period with the most bigrams. However, both P1 and P16 stand out strongly. P17 is extremely weak, but more about that later. Next the results for trigrams:
z340 trigrams
Period 1 -> 42823 <<<-------------- !!! Period 2 -> 9640 Period 3 -> 10647 Period 4 -> 25024 Period 5 -> 26159 Period 6 -> 16770 Period 7 -> 9300 Period 8 -> 20927 Period 9 -> 8647 Period 10 -> 12421 Period 11 -> 15219 Period 12 -> 6313 Period 13 -> 10083 Period 14 -> 9242 Period 15 -> 10414 Period 16 -> 18435 Period 17 -> 8132 <<<-------------- Period 18 -> 18171 Period 19 -> 21730 <<<-------------- Period 20 -> 7664
Here a peak on P1 shows up very clearly. Let’s take a look at the result for quadgrams:
z340 quadgrams
Period 1 -> 9728 <<<-------------- !!! Period 2 -> 0 Period 3 -> 0 Period 4 -> 1381 Period 5 -> 1024 Period 6 -> 0 Period 7 -> 3072 Period 8 -> 3489 Period 9 -> 1534 Period 10 -> 1024 Period 11 -> 1444 Period 12 -> 0 Period 13 -> 0 Period 14 -> 0 Period 15 -> 512 Period 16 -> 2906 Period 17 -> 0 Period 18 -> 0 Period 19 -> 2522 <<<-------------- Period 20 -> 0
P1 is again the most "successful" period. Now the 5-grams:
z340 5-grams
Period 1 -> 0 Period 2 -> 0 Period 3 -> 0 Period 4 -> 128 Period 5 -> 0 Period 6 -> 0 Period 7 -> 0 Period 8 -> 512 Period 9 -> 0 Period 10 -> 0 Period 11 -> 0 Period 12 -> 0 Period 13 -> 0 Period 14 -> 0 Period 15 -> 0 Period 16 -> 0 Period 17 -> 0 Period 18 -> 0 Period 19 -> 0 Period 20 -> 0
On the "half period" exactly a quarter of the bigrams? Well… I guess that’s just a coincidence. I just wanted to show the result to be complete.
Next, a repeat of the first test, but this time only results with 37 or more bigrams were counted:
z340, bigrams >= 37
Period 1 -> 115 Period 2 -> 11 Period 3 -> 0 Period 4 -> 31 Period 5 -> 5 Period 6 -> 0 Period 7 -> 0 Period 8 -> 0 Period 9 -> 0 Period 10 -> 0 Period 11 -> 12 Period 12 -> 0 Period 13 -> 0 Period 14 -> 0 Period 15 -> 0 Period 16 -> 245 Period 17 -> 0 Period 18 -> 3 Period 19 -> 338 Period 20 -> 0
The results seemed a little strange to me. So I did a comparative measurement. I took the first 340 letters of the plaintext from z408, transposed P19 and substituted it with 25% random cycles:
z408 first 340 letters. Transposed P19, 25% random cycles. bigrams:
Period 1 -> 1330 Period 2 -> 12467 Period 3 -> 4893 Period 4 -> 604 Period 5 -> 1782 Period 6 -> 2650 Period 7 -> 1767 Period 8 -> 7049 Period 9 -> 1815 Period 10 -> 1712 Period 11 -> 1831 Period 12 -> 2555 Period 13 -> 3384 Period 14 -> 1392 Period 15 -> 10215 Period 16 -> 2628 Period 17 -> 12 <<<-------------- Period 18 -> 1635 Period 19 -> 79220 <<<-------------- Period 20 -> 11846
This time P19 is very clear and the result is as expected (at least for me). Again, P17 is the low-performer. Well, let’s have a look at the trigrams:
z408 first 340 letters. Transposed P19, 25% cycles. 3-grams:
Period 1 -> 17399 Period 2 -> 14227 Period 3 -> 12930 Period 4 -> 3779 Period 5 -> 10258 Period 6 -> 12339 Period 7 -> 4274 Period 8 -> 10804 Period 9 -> 13484 Period 10 -> 7780 Period 11 -> 20485 Period 12 -> 11583 Period 13 -> 12376 Period 14 -> 10556 Period 15 -> 16229 Period 16 -> 24778 Period 17 -> 0 <<<-------------- !!! Period 18 -> 18119 Period 19 -> 68170 <<<-------------- Period 20 -> 13266
Am I missing something obvious? Why is P17 the low-performer? Coincidence? Let’s do more tests with the same procedure:
Whiskey in the jar. Transposed P19, 25% cycles. 2-grams:
Period 1 -> 9681 Period 2 -> 9105 Period 3 -> 4528 Period 4 -> 19879 Period 5 -> 708 Period 6 -> 74 Period 7 -> 14157 Period 8 -> 2688 Period 9 -> 6080 Period 10 -> 11072 Period 11 -> 898 Period 12 -> 1305 Period 13 -> 15208 Period 14 -> 1240 Period 15 -> 1938 Period 16 -> 3907 Period 17 -> 0 <<<-------------- !!! Period 18 -> 1556 Period 19 -> 43480 <<<-------------- Period 20 -> 10492
Summer of 69. Transposed P19, 25% cycles. 2-grams
Period 1 -> 3843 Period 2 -> 7284 Period 3 -> 3052 Period 4 -> 2243 Period 5 -> 7966 Period 6 -> 8068 Period 7 -> 16155 Period 8 -> 5010 Period 9 -> 5153 Period 10 -> 17979 Period 11 -> 14923 Period 12 -> 12123 Period 13 -> 4262 Period 14 -> 8381 Period 15 -> 6528 Period 16 -> 4202 Period 17 -> 152 <<<-------------- !!! Period 18 -> 14354 Period 19 -> 21349 <<<-------------- Period 20 -> 4247
Plaintext number 3 from Jarlves plaintext library. Transposed P19, 25% cycles. 2-grams:
Period 1 -> 1634 Period 2 -> 16831 Period 3 -> 3607 Period 4 -> 1972 Period 5 -> 1943 Period 6 -> 25129 Period 7 -> 1047 Period 8 -> 7741 Period 9 -> 2140 Period 10 -> 1699 Period 11 -> 2829 Period 12 -> 3419 Period 13 -> 2434 Period 14 -> 2536 Period 15 -> 13201 Period 16 -> 3154 Period 17 -> 0 <<<-------------- !!! Period 18 -> 1269 Period 19 -> 56398 <<<-------------- Period 20 -> 7592
Maybe I’m making a fool of myself right now, but I can’t explain P17 in any way. Either I have a bug in my code or I miss something completely obvious.
I can’t explain the behavior at z340 either. Why are P1 and P16 so successful compared to P19? Maybe it’s all just a coincidence, but something seems to be looming here. Maybe these results come from a very strange transposition. Or they are an indication of a hoax. By very simple manipulations of the cipher relatively high bigram and trigam numbers can be generated. Significantly more than would be expected in a 340 character cipher. The reason for this can of course be a very repetitive plain text. Maybe a simple technique combined with a pattern was used to create a hoax. The pivots could perhaps be explained in this way. But I have to admit: These are all only half-baked ideas at first. Sometimes it helps me to write down thoughts. Even if they are still so confused.
Translated with http://www.DeepL.com/Translator
Period 17 is low because you are just shifting columns up and down, and the message is 17 columns wide. I mean, you aren’t changing anything as far as period 17 goes when you shift columns up and down.
I find your period 1 results very interesting, and period 16 also. It could be evidence of some type of creative transposition. He could have started out with a scytale message, then inscribed that into a rectangle of a different size, shifted stuff around according to some pattern, and transcribed into the 17 x 20 matrix.
If you read the message right left, bottom top, a lot of the period 16 bigrams are the same as the period 19 bigrams reading left right, top bottom.
I have been trying to find patterns that show hoax by manipulating the message, casting it into different shapes, to see if symbols appear only in certain columns or rows, but so far no luck.
The pivots is the real issue to me. We can replicate all other observations, close or pretty much, with different ciphers, but not the pivots. Thanks.
Here a peak on P1 shows up very clearly. Let’s take a look at the result for quadgrams:
Could you provide some examples of the 4-grams that are formed?
Period 17 is low because you are just shifting columns up and down, and the message is 17 columns wide. I mean, you aren’t changing anything as far as period 17 goes when you shift columns up and down.
Oops… I really should have noticed that. Thank you.
If you read the message right left, bottom top, a lot of the period 16 bigrams are the same as the period 19 bigrams reading left right, top bottom.
I’m putting this on my todo list. That’s really interesting, I’ll investigate it more closely.
Could you provide some examples of the 4-grams that are formed?
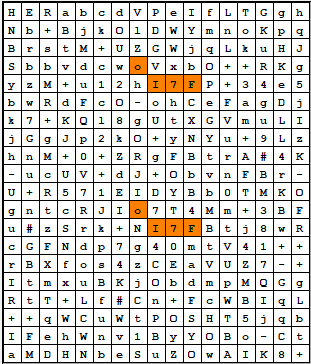
I think I already know the point you’re making. There are actually only 3 different ones:
jCba: 1023 oI7F: 16383 jqL+: 2047
This is my transcription, I use different symbols than in AZDecrypt:
HERabcdVPeIfLTGgh Nb+BjkOlDWYmnoKpq BrstM+UZGWjqLkuHJ SbbvdcwoVxbO++RKg yzM+u12hI7FP+34e5 bwRdFcO-ohCeFagDj k7+KQl8gUtXGVmuLI jGgJp2kO+yNYu+9Lz hnM+0+ZRgFBtrA#4K -ucUV+dJ+ObvnFBr- U+R571EIDYBb0TMKO gntcRJIo7T4Mm+3BF u#zSrk+NI7FBtj8wR cGFNdp7g40mtV41++ rBXfos4zCEaVUZ7-+ ItmxuBKjObdmpMQGg RtT+Lf#Cn+FcWBIqL ++qWCuWtPOSHT5jqb IFehWnv1ByYOBo-Ct aMDHNbeSuZOwAIK8+
The most frequent (oI7F) is very easy to explain:
Well, I guess I’ll have to see if my measuring method makes sense or not.
I think I already know the point you’re making. There are actually only 3 different ones:
I did not know about the "oI7F" 4-gram (assuming that is the point you thought me to made).
Thanks for showing.
AZdecrypt uses doranchak’s CryptoScope 340 transcription: http://www.oranchak.com/zodiac/webtoy/stats.html