Another observation I came across when doing various tests on Z340 has to do with a spike in the bigram IoC at the period of 19 (or step, or distance).
Bigram IoC (index of coincidence) is just another way to measure bigram repeats, but it is more "sensitive" to multiple repeats.
Here’s the raw graph:

Transposition test (encode), bigram IoC:
  1: bic=1.997  |————————————————————————————————————————————————————————————————————————————————
  2: bic=1.515  |—————————————————————————————————————————————————————————————
  3: bic=1.791  |————————————————————————————————————————————————————————————————————————
  4: bic=1.997  |————————————————————————————————————————————————————————————————————————————————
  5: bic=2.135  |——————————————————————————————————————————————————————————————————————————————————————
  6: bic=1.515  |—————————————————————————————————————————————————————————————
  7: bic=1.446  |——————————————————————————————————————————————————————————
  8: bic=1.240  |——————————————————————————————————————————————————
  9: bic=1.515  |—————————————————————————————————————————————————————————————
 10: bic=1.860  |———————————————————————————————————————————————————————————————————————————
 11: bic=1.240  |——————————————————————————————————————————————————
 12: bic=1.102  |—————————————————————————————————————————————
 13: bic=1.240  |——————————————————————————————————————————————————
 14: bic=1.240  |——————————————————————————————————————————————————
 15: bic=1.515  |—————————————————————————————————————————————————————————————
 16: bic=2.066  |———————————————————————————————————————————————————————————————————————————————————
 17: bic=1.997  |————————————————————————————————————————————————————————————————————————————————
 18: bic=1.377  |————————————————————————————————————————————————————————
 19: bic=3.099  |————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————
 20: bic=1.309  |—————————————————————————————————————————————————————
 21: bic=1.997  |————————————————————————————————————————————————————————————————————————————————
 22: bic=1.309  |—————————————————————————————————————————————————————

The first line is the original, un-transposed Z340. As you can see, period 19 shows a spike that increases the bigram IoC by over 50%. The next highest spike is only 7%, and the rest are equal or lower than the original.

What does this mean? One possibility is that bifid encoding was used in Z340, as this test will spike at half the bifid period. But this means that bifid encoding was done with the period of 38 (=19×2). A very odd number to be used as a period for bifid. It is common to use a low number, such as 4 or maybe 5, or you do it across the whole cipher. I can see Z using 17, but 38?!

The other possibility is that a columnar transposition was used: Something like this. I had to add two extra new symbols at the end ($$), so that the cipher can be formatted into a 19×18 matrix, but now you should be able to recognize the original Z340 if you start reading from the top left corner down the column. (I so wish Webtoy would allow reformatting the cipher into a matrix of any dimensions, including incompletely filled ones :).

With this transposition, we now have 30 repeating bigrams (67 repeats total) vs. 21/46 originally. 50% increase, as promised. And even 2 trigram repeats, not related to original ones in any way.

The bad news — it doesn’t solve. I even tried reverse/backwards. Dead end? Or is there something else going on here? I sure hope it’s not bifid. 🙂

That’s it for now. The other entries in my "log of unexplained oddities" are too insignificant/inconclusive to mention (i.e. can easily be attributed to pure chance).

Could lines 1,3,5,7,9etc be one code and 2,4,6,8 etc be another. Which would really mix it up.

Or.. First line read left to right second line read back right to left third left to right etc
Snaking . This would be an easy code to make up. Something simple but something that would trick the decoding process.

Sorry if it’s been tested and I’m wasting your genius minds. Keep up the good work I have a good feeling you guys n gals are going to get a result. It’s been real interesting watching you guys work but rather difficult to follow.
Cheers

The 14 symbols that are not shared is especially significant, I think. That’s 22% our of 63 symbols. I don’t think it can happen by chance. For comparison, I’ve split Z408 the same way, and there is only 1 symbol that’s present in odds and not in evens.

If this observation is significant then we need to look into it, I believe it may be a good lead to transposition of the plaintext. There are other things that may relate towards toward your observation, the "+" symbol and some other high count symbols unwillingness to sit on prime number positions. Some time ago I noted that one cipher in my collection came close to the 340 (via a measurement which may not relate as much to your observation).

tonyb2:

,CurN[?dISMT^yhvo
sdWSPFYwptc+gbfdB
zOR`yA+0ZIG-VYa6+
_C-UroLZD60Zfu4Jb
sdq4{pikGFBJtTc:z
S+:OS]mNjxlIJJWgu
9vP[C,4Yy7UXr`hJs
FclXfN@wtVRKTa8-N
B_oDxZrZsUdliqXj4
dIWn@JSdl9p,XT`kT
U-UlFa[-zX@JhkYq+
b@26gGRdfOyDpcA+V
i20ZBu,dE_oZbT^vj
IGtT`C2ULZn*YW_Pz
ufSU9rUo[sbZFTUWh
w6BGRI_taD-qVrNis
p+nmoWxFVjVtu9T`O
E_,1n^oW[gYJrTy{C
sHhaL]?cR_o-V+ZlD
ibTUdXjq-SgFZfzZl

I’ve looked into the even/uneven thing as well and have done a test in this direction: grille/chessboard cipher. Both even and uneven parts are showing signs of cycling, but less so than for instance the first or last 10 rows.

Thanks for sharing your observations!

Could lines 1,3,5,7,9etc be one code and 2,4,6,8 etc be another. Which would really mix it up.

That’s a good idea. I just tried splitting Z340 into 2 parts by rows as you suggested. Unfortunately these 2 new sequences turned out to be very similar. The only notable difference is that both of the trigram repeats fall entirely on the odd rows. But it can be just a coincidences, since there are only 2 of them.

Or.. First line read left to right second line read back right to left third left to right etc
Snaking . This would be an easy code to make up. Something simple but something that would trick the decoding process.

That has been tried already. Including snaking along columns (up-down, then down-up, etc.). I think another name for this route is "plow path". Just like a farmer plowing a field.

I’ve seen mentions of another type of route: "ox-cart". But I’m not entirely sure what it is. Does anyone know? Google turned out completely useless in that regard.

Sorry if it’s been tested and I’m wasting your genius minds.

Don’t be afraid to come up with ideas that have already been tried! You never know, you might invent something completely novel. Better yet, investigate your own ideas. Even if a similar idea has been tried by someone else, they might’ve made a mistake somewhere along the way, and you could actually be the first to reach the correct solution. The more eyeballs and brains we have looking at this, the more chances we have to solve it.

Keep up the good work I have a good feeling you guys n gals are going to get a result. It’s been real interesting watching you guys work but rather difficult to follow.

I know what you mean. 🙂 I also often have hard time following some things other people are saying here. That’s why I always try to simplify what I’m saying as much as possible. I hope it doesn’t sound too condescending when I’m explaining seemingly trivial things. I’m just trying to make it easier to follow. Besides, no point in saying brilliant genius things when nobody can understand you, right? 🙂

Could lines 1,3,5,7,9etc be one code and 2,4,6,8 etc be another. Which would really mix it up.

Or.. First line read left to right second line read back right to left third left to right etc
Snaking . This would be an easy code to make up. Something simple but something that would trick the decoding process.

Sorry if it’s been tested and I’m wasting your genius minds. Keep up the good work I have a good feeling you guys n gals are going to get a result. It’s been real interesting watching you guys work but rather difficult to follow.
Cheers

Hey Mr lowe,

I have tested all possible combinations of flipping rows – a snake pattern is one of them – more than 2 million ciphers were checked this way with AZdecrypt: row flips. It’s not conclusive but I would say unprobable. — I also have a good feeling about it! Actually since the start of this year I felt that the 340 is going to get solved, somehow, this year. Keep on dreaming right?

I’ve seen mentions of another type of route: "ox-cart". But I’m not entirely sure what it is. Does anyone know? Google turned out completely useless in that regard.

I think it, too, is a "plow path". The one example I’ve seen (kfreeze’s ox-cart version of the 340 which is one of the available ciphers here http://zodiackillerciphers.com/webtoy/stats.html ) has every other row reversed.

Some time ago I noted that one cipher in my collection came close to the 340 (via a measurement which may not relate as much to your observation).tonyb2:

Ah, I recognize that cipher. It’s one of the ciphers that my auto-solver struggles to crack (i.e. it takes a lot of restarts before it converges on the correct solution). Actually, both "tonyb" ciphers are hard to crack (the other one starts with "jfHQC…"). And they both have similarly low bigram repeats, although Z340 still beats them both (no doubt due to the 2nd half having practically no bigram repeats at all). I tried finding out how "tonyb1/2" were constructed. Was the main goal to have as few bigram repeats? And the author tried his best and still couldn’t beat Z340? Was the plaintext chosen very carefully? Or homophones? Or both? Unfortunately I couldn’t find anything as it’s been a long time since they were created.

@daikon,

It was before my time but I think they were created to fool ZKDecrypto and failed. I believe tonyb2 may have similar symbol differences in parts as you observed with the 340, at least one my measurements suggest so.

Hmm, something else I just noticed that might fit the theory of odd symbols being nulls.
Looking at Z13 cipher:

If we split it into odds and evens, we end up with,
Evens: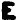
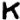
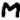
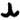
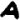
Odds: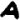

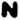
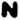
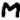
Notice that the newly introduced, never before seen, 8-in-a-circle symbol falls entirely into odds. Also, odds have a lot of repeats, while evens don’t have a single repeating symbol. If we follow the theory that odds=nulls, then this cipher could very well solve to simply: "ZODIAC" (notice no repeating letters). As in: "My name is ZODIAC".

One small kink. Technically, this symbol is also new:

But it can be argued that it was supposed to be the same as , but Z’s hand slipped. Or even , but Z forgot to add the line at the top.

It could also be completely coincidental, of course, as Z13 is just too short. 🙂

Let’s also look at Z32 cipher (map code), while we are at it:

Evens:
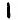
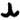
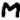
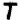
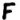
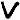
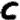
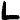
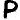
Odds: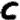

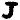
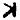
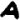
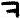
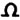
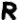
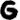
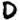
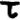
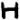
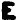
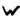
Once again, the new, never before seen, symbol "omega" falls into odds (i.e. random filler, nulls). Otherwise I can’t really make any other meaningful observations. Well, maybe that the odds seem to spell out "GOD THE (zodiac symbol)" towards the end (signature of sorts?). Since the odds are supposed to be random filler, I can sort of see Z having some fun with it, spelling out stuff to confuse decryptors.

P.S. I so wish Webtoy would use consistent ASCII mapping across all Z ciphers! I nearly missed the fact that the same letters in Z13/Z32/Z340 map to entirely different symbols in each cipher. For example, 8 in Z13 is not the same symbol as 8 in Z340. Which is why I’m using actual pictograms in this post, and not ASCII, to avoid any confusion.

Here’s a few things I noticed about Z340 when doing different experiments with it. Things that stand out, but didn’t lead to any breakthroughs (obviously). I thought I’d share my observations just in case someone else can make some further conclusions, or it might help lead to the solution in some other way.

Splitting Z340 into odd and even symbols (i.e. only symbols at odd or even positions) produces 2 very different sequences:
Odd symbols
Even symbols

Statistically they should be very similar, as English language has absolutely no preference towards odd/even letters that I know of, or odd/even lengths of words, etc. And yet…

Odd symbols:
Very low number of bigram repeats (only 2!).
No trigram repeats, or higher N-grams.
58 unique symbols, so 5 symbols are missing: & 1 @ A t.

Even symbols:
Good number of bigram repeats (9). About the expected for the cipher this length — Z408 had 10 bigram repeats in the first 170 symbols.
2 trigram repeats. Again, about expected — Z408 also had 2 trigram repeats in the first 170 symbols. These 2 trigram repeats are not overlapping with the 2 trigram repeats in the full Z340 in any way, so they were created anew.
54 unique symbols, so 9 symbols are missing: 3 7 ; J M U X b j.

The 14 symbols that are not shared is especially significant, I think. That’s 22% our of 63 symbols. I don’t think it can happen by chance. For comparison, I’ve split Z408 the same way, and there is only 1 symbol that’s present in odds and not in evens.

Symbol counts (frequencies) do not match at all either. For example, the 3rd most frequent symbol for "odds" (‘M’) is completely missing in "evens". 2nd most frequent symbol for "evens" (‘2’) only appears twice in "odds". The only exception is ‘+’, which is the top symbol for both, but most of ‘+’s went into "evens": 14 vs 10 for "odds".

What could this possibly mean? The obvious conclusion — the odd symbols are just random noise, filler inserted to confuse decryptors, they are nulls that should be dropped. However, the odds sequence does have a fairly expected frequency distribution, so it might be part of the message, just encrypted differently from the evens sequence.

I tried feeding each of the 2 sequences into an auto-solver, but didn’t get a coherent solution. The issue might be the very high multiplicity, so it could be that we have the correct extra transposition that Z did to Z340, but the resulting 170 symbol cipher is too short to be cracked. I’ve tried combining the 2 sequences, by appending one to another, and then the other way around, but didn’t get a solve either way. Maybe they should be recombined in some other way?

Another issue with this (and I’m playing devil’s advocate now ), is that Z clearly liked to use a matrix with 17 characters in a row. It’s an odd number, so odd/even positions alternate (or flip around) for every other row. I’ll demonstrate with a matrix of width 7, and use 0 for odd positions and 1 for even positions:
0101010
1010101
0101010
1010101

So if he did use odds/evens split, it would make more sense, and would be easier to do with a pen and paper, if done per row. I.e. restart odd/even counts for each new row. I’ve tried decomposing Z340 this way, but ended up with 2 unremarkable sequences, of slightly different lengths, but with very similar stats. On the other hand, maybe Z realized that doing odds/evens across the whole cipher would result in a "checkerboard pattern" I showed above, and maybe he thought that it would be more confusing and harder to crack, and went with it.

I spent a few minutes making my cycle spreadsheet so that conditional formatting shows whether a symbol is odd or even. Then I looked at the top scoring cycles on the 340 to see if any of the 34 highest scoring cycles (score 256 or more) are exclusively odd – even – odd – even, etc., or exclusively odd or exclusively even.

There are nine symbols unique to the odds:

37, 38, 41, 43, 45, 49, 58, 59, and 61.

38 is an even numbered symbol, but first appears at position 41 and 58 is an even numbered symbol but first appears at position 109.

There are five symbols unique to the evens:

12, 48, 52, 60 and 62.

37 cycles with 41 in the top thirty four cycles, and 38 cycles with 41 in the top thirty four cycles. EDIT: There are 1953 total cycles. Twenty three cycles score in the 256 range. When I randomize the 340, I get an average of 6.1 such cycles. The 37 – 41 cycle has the familiar repetition of the last symbol toward the end.

37 41 37 41 37 41 37 41 37 37 37
38 41 38 41 38 41 38 41 38

It could just be a coincidence and those are the only patterns that I can find. There is no high scoring cycle that is odd – even – odd – even, etc. I am going to try to conditional format for 3 parts and 4 parts and look for patterns there too.

EDIT: I checked the top 34 two symbol cycles for cycled 3 keys, 4 keys and 5 keys. My findings are that there are no other high scoring cycles that are all in the same parts or cycle with the parts. In other words, there is no other cycle that occurs on only one part, or Part 1, then Part 2, then Part 3, then Part 1 again, etc.

See: viewtopic.php?f=81&t=2617&start=210

Odd symbols:
Very low number of bigram repeats (only 2!).
No trigram repeats, or higher N-grams.
58 unique symbols, so 5 symbols are missing: & 1 @ A t.

Even symbols:
Good number of bigram repeats (9). About the expected for the cipher this length — Z408 had 10 bigram repeats in the first 170 symbols.
2 trigram repeats. Again, about expected — Z408 also had 2 trigram repeats in the first 170 symbols. These 2 trigram repeats are not overlapping with the 2 trigram repeats in the full Z340 in any way, so they were created anew.
54 unique symbols, so 9 symbols are missing: 3 7 ; J M U X b j.

The 14 symbols that are not shared is especially significant, I think. That’s 22% our of 63 symbols. I don’t think it can happen by chance. For comparison, I’ve split Z408 the same way, and there is only 1 symbol that’s present in odds and not in evens.

Symbol counts (frequencies) do not match at all either. For example, the 3rd most frequent symbol for "odds" (‘M’) is completely missing in "evens". 2nd most frequent symbol for "evens" (‘2’) only appears twice in "odds". The only exception is ‘+’, which is the top symbol for both, but most of ‘+’s went into "evens": 14 vs 10 for "odds".

What could this possibly mean? The obvious conclusion — the odd symbols are just random noise, filler inserted to confuse decryptors, they are nulls that should be dropped. However, the odds sequence does have a fairly expected frequency distribution, so it might be part of the message, just encrypted differently from the evens sequence.

Sorry to necro this old thread but I am looking more deeply into unigrams unique/exclusive to other periods in function of the unigram distance anomaly in a broad sense.

Looking at odd/even (2 columns) there are 31 unigrams unique to the first column and 12 unigrams unique to the second column for a total of 43. Versus randomizations of the 340 it is a 1.92 sigma observation and verus plaintext + encodings with cycle randomization to match the 340 it is a 2.03 sigma observation. It appears not to be a property of sequential homophonic substitution and it being a 2 sigma observation makes it at least a little bit curious.

Looking at 3 columns there are 6 unigrams unique to the first column, 9 unigrams unique to the second column and 5 unigrams unique to the third column for a total of 20. Versus randomizations of the 340 it is a 1.61 sigma observation and verus plaintext + encodings with cycle randomization to match the 340 it is a 1.02 sigma observation. With 3 columns there is a positive correlation with sequential homophonic substitution.

Looking at 6 columns … (2, 5, 3, 2, 0, 2) for a total of 14. Versus randomizations of the 340 it is a 3.35 sigma observation and verus plaintext + encodings with cycle randomization to match the 340 it is a 1.51 sigma observation. With 6 columns there is a positive correlation with sequential homophonic substitution.

I have tested only the column sizes that appeared interesting. For column sizes larger than 2 it appears to be a property of sequential homophonic substitution.

AZdecrypt periodic unique unigrams stats for: 340.txt
--------------------------------------------------------
Period 1:
- Row/column 1: 340, 340 (100%)
Period 2:
- Row/column 1: 5, 31
- Row/column 2: 0, 12 (11.62%)
Period 3:
- Row/column 1: 2, 6
- Row/column 2: 1, 9
- Row/column 3: 0, 5 (15%)
Period 4:
- Row/column 1: 0, 2
- Row/column 2: 1, 3
- Row/column 3: 0, 0
- Row/column 4: 0, 0 (20%)
Period 5:
- Row/column 1: 0, 0
- Row/column 2: 3, 2
- Row/column 3: 0, 0
- Row/column 4: 0, 8
- Row/column 5: 0, 2 (25%)
Period 6:
- Row/column 1: 0, 2
- Row/column 2: 0, 5
- Row/column 3: 1, 3
- Row/column 4: 0, 2
- Row/column 5: 0, 0
- Row/column 6: 0, 2 (7.14%)
Period 7:
- Row/column 1: 0, 1
- Row/column 2: 0, 0
- Row/column 3: 1, 0
- Row/column 4: 0, 0
- Row/column 5: 0, 0
- Row/column 6: 0, 0
- Row/column 7: 0, 0 (100%)
Period 8:
- Row/column 1: 0, 2
- Row/column 2: 0, 2
- Row/column 3: 0, 0
- Row/column 4: 1, 0
- Row/column 5: 0, 0
- Row/column 6: 0, 1
- Row/column 7: 0, 0
- Row/column 8: 0, 0 (20%)
Period 9:
- Row/column 1: 0, 2
- Row/column 2: 0, 0
- Row/column 3: 0, 0
- Row/column 4: 1, 0
- Row/column 5: 0, 0
- Row/column 6: 0, 0
- Row/column 7: 0, 2
- Row/column 8: 0, 1
- Row/column 9: 0, 0 (20%)
Period 10:
- Row/column 1: 0, 0
- Row/column 2: 0, 2
- Row/column 3: 0, 0
- Row/column 4: 1, 1
- Row/column 5: 0, 2
- Row/column 6: 0, 0
- Row/column 7: 0, 0
- Row/column 8: 0, 0
- Row/column 9: 0, 3
- Row/column 10: 0, 0 (12.5%)
Period 11:
- Row/column 1: 0, 0
- Row/column 2: 0, 1
- Row/column 3: 0, 0
- Row/column 4: 0, 0
- Row/column 5: 1, 0
- Row/column 6: 0, 2
- Row/column 7: 0, 0
- Row/column 8: 0, 0
- Row/column 9: 0, 0
- Row/column 10: 0, 0
- Row/column 11: 0, 0 (33.33%)
Period 12:
- Row/column 1: 0, 0
- Row/column 2: 0, 1
- Row/column 3: 0, 0
- Row/column 4: 0, 0
- Row/column 5: 1, 0
- Row/column 6: 0, 0
- Row/column 7: 0, 0
- Row/column 8: 0, 0
- Row/column 9: 0, 0
- Row/column 10: 0, 2
- Row/column 11: 0, 0
- Row/column 12: 0, 0 (33.33%)
Period 13:
- Row/column 1: 0, 0
- Row/column 2: 0, 0
- Row/column 3: 0, 0
- Row/column 4: 0, 1
- Row/column 5: 0, 0
- Row/column 6: 1, 0
- Row/column 7: 0, 0
- Row/column 8: 0, 0
- Row/column 9: 0, 0
- Row/column 10: 0, 0
- Row/column 11: 0, 0
- Row/column 12: 0, 0
- Row/column 13: 0, 0 (100%)
Period 14:
- Row/column 1: 0, 0
- Row/column 2: 0, 0
- Row/column 3: 0, 0
- Row/column 4: 0, 0
- Row/column 5: 0, 0
- Row/column 6: 1, 0
- Row/column 7: 0, 0
- Row/column 8: 0, 1
- Row/column 9: 0, 0
- Row/column 10: 0, 0
- Row/column 11: 0, 0
- Row/column 12: 0, 0
- Row/column 13: 0, 0
- Row/column 14: 0, 0 (100%)
Period 15:
- Row/column 1: 0, 0
- Row/column 2: 0, 0
- Row/column 3: 0, 0
- Row/column 4: 0, 0
- Row/column 5: 0, 0
- Row/column 6: 1, 0
- Row/column 7: 0, 2
- Row/column 8: 0, 0
- Row/column 9: 0, 0
- Row/column 10: 0, 0
- Row/column 11: 0, 0
- Row/column 12: 0, 0
- Row/column 13: 0, 0
- Row/column 14: 0, 1
- Row/column 15: 0, 0 (33.33%)
Period 16:
- Row/column 1: 0, 2
- Row/column 2: 0, 0
- Row/column 3: 0, 0
- Row/column 4: 0, 0
- Row/column 5: 0, 0
- Row/column 6: 0, 1
- Row/column 7: 1, 0
- Row/column 8: 0, 0
- Row/column 9: 0, 0
- Row/column 10: 0, 0
- Row/column 11: 0, 0
- Row/column 12: 0, 0
- Row/column 13: 0, 0
- Row/column 14: 0, 0
- Row/column 15: 0, 0
- Row/column 16: 0, 0 (33.33%)
Period 17:
- Row/column 1: 0, 0
- Row/column 2: 0, 0
- Row/column 3: 0, 0
- Row/column 4: 0, 0
- Row/column 5: 0, 0
- Row/column 6: 0, 0
- Row/column 7: 1, 0
- Row/column 8: 0, 0
- Row/column 9: 0, 0
- Row/column 10: 0, 0
- Row/column 11: 0, 0
- Row/column 12: 0, 0
- Row/column 13: 0, 0
- Row/column 14: 0, 0
- Row/column 15: 0, 1
- Row/column 16: 0, 0
- Row/column 17: 0, 0 (100%)
Period 18:
- Row/column 1: 0, 0
- Row/column 2: 0, 0
- Row/column 3: 0, 0
- Row/column 4: 0, 0
- Row/column 5: 0, 0
- Row/column 6: 0, 0
- Row/column 7: 0, 2
- Row/column 8: 1, 1
- Row/column 9: 0, 0
- Row/column 10: 0, 0
- Row/column 11: 0, 0
- Row/column 12: 0, 0
- Row/column 13: 0, 0
- Row/column 14: 0, 0
- Row/column 15: 0, 0
- Row/column 16: 0, 0
- Row/column 17: 0, 0
- Row/column 18: 0, 0 (33.33%)
Period 19:
- Row/column 1: 0, 1
- Row/column 2: 0, 0
- Row/column 3: 0, 0
- Row/column 4: 0, 0
- Row/column 5: 0, 0
- Row/column 6: 0, 0
- Row/column 7: 0, 0
- Row/column 8: 1, 0
- Row/column 9: 0, 0
- Row/column 10: 0, 0
- Row/column 11: 0, 0
- Row/column 12: 0, 0
- Row/column 13: 0, 0
- Row/column 14: 0, 0
- Row/column 15: 0, 0
- Row/column 16: 0, 0
- Row/column 17: 0, 0
- Row/column 18: 0, 0
- Row/column 19: 0, 0 (100%)
Period 20:
- Row/column 1: 0, 0
- Row/column 2: 0, 2
- Row/column 3: 0, 0
- Row/column 4: 0, 0
- Row/column 5: 0, 0
- Row/column 6: 0, 0
- Row/column 7: 0, 0
- Row/column 8: 1, 0
- Row/column 9: 0, 0
- Row/column 10: 0, 0
- Row/column 11: 0, 0
- Row/column 12: 0, 0
- Row/column 13: 0, 0
- Row/column 14: 0, 1
- Row/column 15: 0, 0
- Row/column 16: 0, 0
- Row/column 17: 0, 0
- Row/column 18: 0, 0
- Row/column 19: 0, 0
- Row/column 20: 0, 0 (33.33%)

Interesting observations, Jarlve. I also re-read this thread and updated http://zodiackillerciphers.com/wiki/ind … servations. There are so many observations to keep up with. I’m wondering if there is a better way to keep it all organized. For example, I have a separate extensive spreadsheet that tracks all of my "features or phantoms" experiments, which compare observations to randomizations.

I still want to drive towards comparing all of these unusual observations to a wide assortment of classical cipher schemes.

Also, Jarlve, why do you think column period greater than 2 shows unigram biases that reflect sequential homophonic substitution? Why would specific symbols still tend to fall in specific columns (versus more random placement)? I can’t think of why certain high frequency letters would align with specific columns.

Interesting observations, Jarlve. I also re-read this thread and updated http://zodiackillerciphers.com/wiki/ind … servations. There are so many observations to keep up with. I’m wondering if there is a better way to keep it all organized. For example, I have a separate extensive spreadsheet that tracks all of my "features or phantoms" experiments, which compare observations to randomizations.

Thanks to mention the update. You could create a document "observation sigmas" that lists a description of the observation and test, the observer and sigma.

I still want to drive towards comparing all of these unusual observations to a wide assortment of classical cipher schemes.

I think we are slowly getting there anyway.

Also, Jarlve, why do you think column period greater than 2 shows unigram biases that reflect sequential homophonic substitution? Why would specific symbols still tend to fall in specific columns (versus more random placement)? I can’t think of why certain high frequency letters would align with specific columns.

It must have to do with the sequential property of the ciphertext.

Example cycle:

ABCDEABCDEABCDEABCDEABCDE

Example cycle by 5 columns:

ABCDE
ABCDE
ABCDE
ABCDE
ABCDE

Sensible?