That’s interesting, smokie. It reminds me of the "multiples of 5" harmonic that occurs when normalizing columnar IoC measurements:

http://www.zodiackillersite.com/viewtop … 442#p48442

I am not sure what, if any, significance there is to this phenomenon.

Good luck with your talk next week doranchak!

Thank you!

Thank you for the test, the results are very clear. Rearrangement of rows is a possible cause for the high unigram distance in the 340 as it could either decrease or increase the value. Your test suggests that the value of the 340 is however quite rare and therefore more unlikely to have been caused by rearrangement of rows, right?

I really don’t know. I have become very reluctant to make any conclusions based solely on the rareness suggested by shuffle tests, because there are other considerations that must be made. For example, throwing a golf ball into a field of grass will hit a blade of grass. From the blade’s perspective, it was a rare one-in-a-billion event. But from the golf ball’s perspective, it was almost certainly going to hit a blade of grass. So when I see a rare phenomenon, I have to wonder: Are there many other blades of grass I’m not considering?

Your example cipher decreases the unique sequence length 17 repeats from 26 to 18 and since we know that is a very significant observation perhaps you could use it to filter out false positives.

That might be an effective method, but I also wonder if it is a side effect of the procedure that weakened the cycles and/or bigrams.

Here are my 2 most likely hypotheses for the high unigram distance in the 340:
1. The high unigram distance of the 340 is related to the group of symbols that do not appear in the middle 7 rows (as marie said).
2. A long key (as Largo said) is used in the homophonic substitution process and some of the most frequently occuring symbols are for whatever reason not part it or are wildcards. Likely hypotheses for the symbols that were not taken up in the homophonic substitution or are wildcards are that these are 1:1 substitutes, plaintext nulls or wildcards (as smokie said). I would like to go as wide as possible with the interpretation of wildcards.
In your test my cipher jarlve2 very closely matches the 340 which is hypothesis 2. Some things to look in may be exotic cycling types (again) such as palindromic cycling which also increases unigram distance and not trying to repeat symbols in a certain view window as opposed to actively cycling homophones.

Interesting ideas – these sound worth exploring. I wonder if Zodiac would have bothered to hide the cycling effect of symbol assignments. He may not have been aware of that particular weakness of homophonic substitution (i.e. brute force searches of cycles), since Z408 was broken mostly with identification of other repeating patterns and trial and error guesses of certain words and phrases.

I re-drafted into 4 to 85 columns and didn’t see any recognizable patterns.

I think that if you slid a lot of plaintext through a 17 x 20 grid you would easily find low frequency letters that appear at the top and bottom of the message, but not in the middle. If you encoded a lot of plaintext in chunks of 340 they would show through. But… packing 63 symbols into a key to get similar symbol count distributions maybe they wouldn’t show through in pairs like this. I noticed that most of the same symbols appear at both the top and the bottom of the message. It’s not like some symbols appear at the top and some at the bottom but with the same overall high score. There is a bi-regional bias.

Maybe the score should reflect whether the symbol appears in both the top and bottom half of the message ( if it doesn’t already ). The test could be: 1. Does the symbol appear in both top and bottom half? 2. If yes, then calculate the distances.

We tried palindromic cycling and determined that it is not. But maybe there is some other creative cycling method.

I think that it could be evidence of the cipher. I skim or read through writings about cryptography hoping to trigger recognition or ideas. I am reading through Mysterious Messages by Gary Blackwood right now. I found it in the children’s section of the library. It’s not advanced mathematics or cryptanalyst stuff, but tells a lot of interesting stories about types and uses of cryptography since the days of the ancient Greeks. People have created a lot of different types of ciphers on their own, to be used and sometimes forgotten for centuries.

I think that there is a good possibility that Zodiac just combined some classical ciphers. Homophonic was used in the Renaissance era. Leon Battista Alberti also invented his disk for Pope Paul II in 1466. It was used to make polyalphabetic cryptograms, but not necessarily by rotating the disk at each plaintext. It could be rotated after an agreed count of plaintext or words.

I wonder if it could be Alberti + homophonic that creates a phantom spike in period x repeats. Or transposition + Alberti + homophonic, but just only a few rotations of the disc. I can imagine Zodiac making a cardboard Alberti disk. I wonder if such a cipher could make one symbol unlike the others ( the + ). And then there is the regional bias of the period 39 repeats to consider.

Speaking of the +, one time a couple of years ago I generated route transposition + homophonic messages, then randomly plopped 24 of one symbol into the message. There weren’t very many bigram repeats at the route period that had the + included. But with the 340, there are.

EDIT: If Zodiac had a book about cryptography that discussed ciphers in chronological order, then Alberti would have been right next to homophonic. Just saying.

I encoded some messages from the library all perfect cycles but with one polyphone and got scores higher than 15034. It was pretty easy.

Message 92 score 15411

46 40 42 24 32 18 20 1 9 7 36 30 11 50 37 51 21
12 5 2 43 38 33 59 39 16 8 3 34 52 35 13 57 19
44 4 47 48 58 11 56 14 10 6 15 60 36 32 9 53 22
11 49 23 12 13 41 17 37 28 10 11 1 33 9 50 20 14
16 29 38 7 26 46 17 2 25 45 28 59 42 3 34 51 39
52 21 15 47 22 11 4 43 48 12 11 18 13 44 53 36 5
14 16 45 15 11 37 17 50 23 12 24 42 57 38 39 29 60
58 25 35 51 13 43 8 36 1 52 49 53 20 14 11 50 44
15 2 31 46 47 3 32 19 37 16 30 11 28 51 24 33 18
48 34 38 57 4 35 10 21 25 19 22 7 29 39 54 9 49
18 45 11 61 12 10 52 23 13 40 1 11 53 55 42 14 46
36 17 50 20 15 47 27 59 37 32 28 60 2 33 11 3 19
29 12 51 43 38 54 6 28 13 9 52 21 14 48 41 44 24
34 18 53 25 31 15 11 4 49 12 39 16 40 11 11 50 55
45 13 5 42 36 37 26 1 35 10 46 27 59 24 51 43 38
9 14 52 22 15 58 2 44 30 3 25 45 47 11 12 26 24
32 19 41 42 13 60 4 33 10 57 23 14 34 25 53 48 58
24 35 18 49 8 43 39 11 46 15 9 50 20 11 47 54 32
51 21 12 59 7 11 48 52 1 31 13 33 2 8 25 34 19
49 22 3 10 36 57 37 35 53 23 14 29 4 32 9 28 55

Message 9 score 15432

15 23 43 47 51 52 19 24 32 17 16 36 44 53 20 11 30
37 54 21 12 45 11 38 9 39 55 33 10 46 13 48 49 51
22 14 5 1 6 61 2 34 9 40 56 52 19 25 31 53 11
5 11 10 26 35 3 42 55 23 12 54 43 36 37 30 4 32
9 41 28 1 7 13 2 33 24 8 14 6 3 18 38 34 20
25 50 21 11 4 10 39 44 59 45 26 35 17 7 29 11 11
22 47 36 56 51 37 15 23 8 12 60 1 52 13 46 38 43
57 14 44 62 7 39 28 9 59 2 53 11 45 3 32 10 40
29 4 8 12 54 19 13 31 11 33 5 1 6 61 48 20 14
2 9 3 34 10 7 21 4 35 18 11 36 16 11 12 32 51
37 27 13 14 41 52 22 11 30 8 38 28 9 60 1 46 31
53 19 12 15 13 14 54 59 24 11 20 2 21 39 51 60 3
52 11 43 5 4 17 25 16 53 22 12 10 11 7 54 36 44
8 1 33 34 37 11 6 13 40 45 14 49 11 35 51 50 38
39 32 18 26 58 12 5 2 6 62 3 30 55 47 52 4 46
9 15 11 36 53 5 1 54 19 23 33 6 13 10 56 48 14
11 59 37 51 2 5 29 11 49 41 38 39 34 16 55 28 50
52 11 3 17 4 29 28 36 35 37 15 60 1 53 12 43 47
38 31 13 2 9 57 24 48 14 49 54 44 39 32 18 11 45
25 16 11 20 12 7 11 33 58 56 29 50 26 36 34 47 3

Message 56 score 15775

48 21 12 59 1 49 62 41 56 37 19 2 38 10 5 13 3
57 52 25 17 56 31 6 57 53 39 42 60 50 22 14 26 51
7 4 54 55 15 46 16 11 12 40 10 11 12 1 10 48 23
13 27 49 37 43 12 52 24 14 18 28 47 50 53 2 38 11
51 21 15 59 25 32 33 39 44 54 8 16 55 22 12 34 3
48 12 26 31 4 63 12 60 1 29 13 40 27 20 23 52 49
53 24 28 37 30 25 38 19 2 5 41 56 54 35 62 39 14
61 55 58 26 9 12 27 36 35 3 63 6 15 50 21 16 59
28 32 33 7 12 52 22 13 8 14 4 57 53 25 17 56 34
5 31 42 40 10 54 23 12 55 6 1 7 62 51 26 12 48
37 15 2 46 52 24 16 32 27 53 54 33 12 49 55 43 47
13 3 38 11 60 4 34 29 50 10 44 59 39 12 21 14 11
12 46 30 1 31 32 15 63 16 2 9 22 12 58 13 40 28
37 20 3 8 41 57 52 51 14 58 15 38 42 47 36 4 62
5 16 48 23 12 60 25 33 34 6 13 53 24 14 49 21 12
45 15 31 63 7 32 56 16 12 62 13 10 8 46 43 59 39
14 54 55 12 22 1 52 50 2 26 11 40 44 60 23 15 37
27 3 51 29 16 10 24 12 47 18 41 46 4 11 12 53 13
28 38 21 25 19 22 48 9 23 42 43 33 5 57 54 35 1
63 6 14 26 55 59 27 34 31 39 44 12 7 15 16 28 52

In fact, as I increased the randomization of my symbol selection, the scores were lower and it was more difficult to get 15034. You might want to check that.

I think that the bi-regional bias is what we should be looking at. There really is one and it does show up in the pictures that emphasize the 15034 score. The absence of some symbols in the middle third of the message, roughly, but presence of the same symbols in the top and bottom third, roughly, seems more important to me. There are a lot of them.

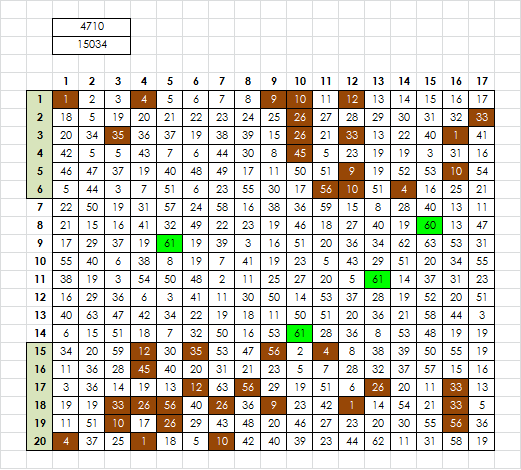
Here is the 340, with symbols that only appear in the top and bottom six rows.

I made up a new score, which may in the future turn out to be trash. For each symbol, I find the average distance from the center of the message to the position(s). Thus, if symbol A appears at positions 37 and 244, the distances, rounded, are 134 and 73. The average is 103. Then, I add up the average distance from center for each symbol that appears exclusively in the top and bottom six rows. It’s sort of arbitrary, but the picture in the first post shows symbols in the top and bottom six rows so I went with that.

A symbol that appears in row 6 and row 15 will have a lower average than a symbol that appears in rows 1 and 15, which would be lower than a symbol that appears in rows 1 and 20. It takes into account both quantity and distance.

The 340 has a score of 4710.

With perfect cycles, I can easily match the 15034 score, but not get even close to the 4710 score. With 25% randomization, which is what the 340 is, roughly over all, I still can’t get close.

The green symbols are the ones that are exclusive to the middle eight rows. Maybe not score so much, but region is important. Please check.

Oh, by the way, thanks for giving the speech doranchak in advance. Maybe someone in the audience will be crazy enough to get involved with this. Try to generate some enthusiasm.

I encoded some messages from the library all perfect cycles but with one polyphone and got scores higher than 15034. It was pretty easy.

Yes, it is what Largo referred to as a long key in this thread, or a key where the frequency distribution is as flat as possible. Your messages have a lower ioc than the 340 which makes it easier to attain higher unigram distance values.

I think that the bi-regional bias is what we should be looking at. There really is one and it does show up in the pictures that emphasize the 15034 score. The absence of some symbols in the middle third of the message, roughly, but presence of the same symbols in the top and bottom third, roughly, seems more important to me. There are a lot of them.

I agree that it seems to be the more likely cause of the high unigram distance. What is the cause of a reasonably large group of symbols not appearing in the middle 3rd of the cipher?

Here is the 340, with symbols that only appear in the top and bottom six rows.

Thank you for the clear picture.

What is the cause of a reasonably large group of symbols not appearing in the middle 3rd of the cipher?

on’t

I don’t know but I am going to work on this idea further.

That might be an effective method, but I also wonder if it is a side effect of the procedure that weakened the cycles and/or bigrams.

In that case I think it would be more likely to have been caused by a symbol thing rather than transposition.

If Zodiac used sequential homophonic substitution for a reason (rather than picking homophones at random) then the only thing I can think of is that it was to hide unigram repeats over short/medium distances. In the 340 there are very few unigram repeats over short distances, especially when taking in consideration its higher ioc per cipher length than the 408. This is why we see 9 rows which have no repeats, it is not easily connected to transposition after/during encoding and typical encoding randomization.

So I came the conclusion that if Zodiac tried to hide unigram repeats he could have done it another way, by not trying to repeat symbols in a given window of his view, without having to keep track of the cycles. The statistics of the 340 seem to agree: low unigram repeats over short/medium distance, high unique sequence peak of 26 at length 17, no apparent homophonic sequences such as in the 408. A silver bullet.

The higher randomness may be due in part or whole to greater care by the writer to not repeat characters on these lines.

Basically, I am Zodiac and encoding along. I say, "Have I used symbol X in the last row?". If the answer is yes, and I want to encode another plaintext that X maps to, I will use symbol Y instead, which also maps to that plaintext.

New spreadsheet, I can work with any shaped message.

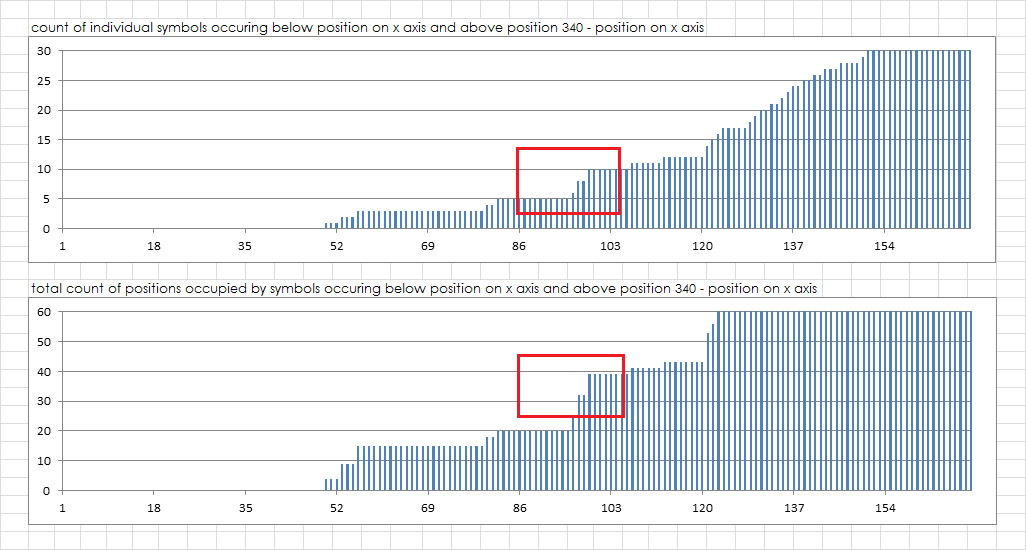
I slide LRTB from position to position, and RLBT from position to position at the same time. At each position, I iterate through all of the symbols, and ask, does the symbol occur below the leftmost position, above the rightmost position, but not in between. If so, then I count +1, and I also count the number of symbols that occur within those criteria.

The 340 as is. There is a jump on row 6. Basically, the top chart shows that there are 10 symbols that appear exclusively on rows 1-6 and 15-20. The bottom chart shows that the symbols occupy a total of 39 positions. Then both graphs level out on row 7, and start climbing again on row 8.

I can set the threshold position to highlight, here at 102.

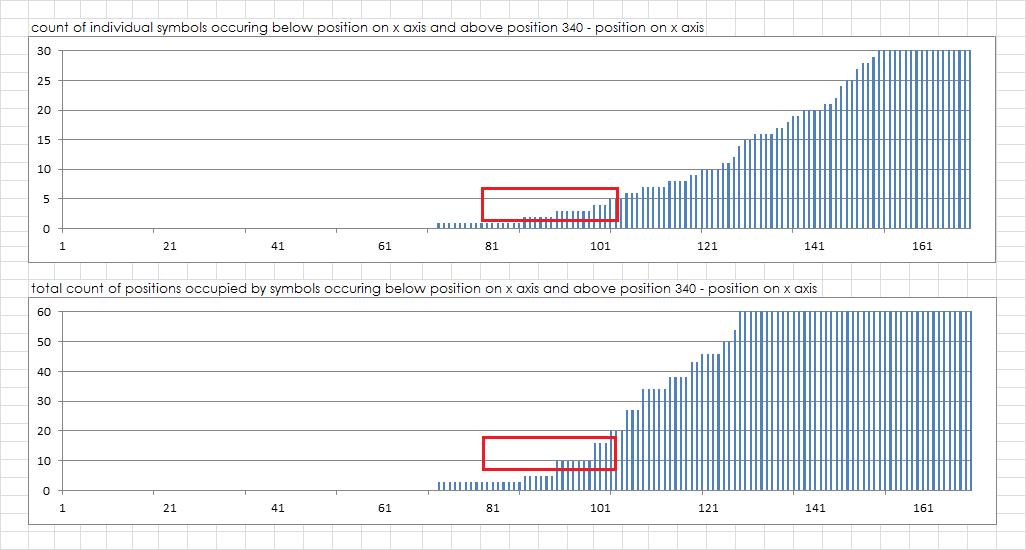
The 340, but rearranged so that the left column becomes the top row and the top row becomes the left column and the message is 20 x 17. Rotated 90 degrees and then mirrored.

At 5 rows, 100 positions almost exactly the same area as 6 rows in a 17 x 20, there are only four total symbols exclusive to rows 1-5 and 13-17. There are only sixteen positions occupied. That is less.

Basically, there are more than twice as many symbols and positions occupied exclusive to the top and bottom 6 rows as compared to the top and bottom 5 rows with the message turned sideways.

Jarlve,

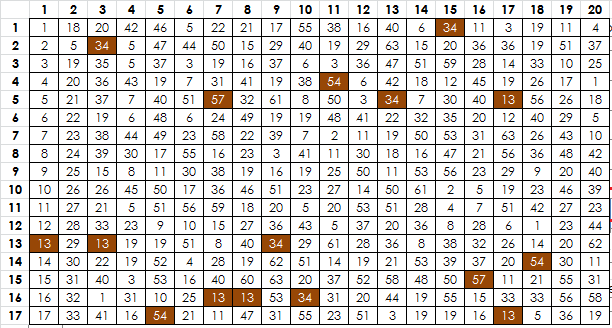
Here is a message that you may solve if you want to. It is probably not like the 340 in a lot of respects. I haven’t checked all of the stats. The only goal was to see if I could generate a message using two different keys and with a bigram repeat spike and a lot of symbols and positions occupied that are exclusive to rows 1-6 and 15-20.

1. Message from library
2. Transposed at period 20. Inscription 17 x 20 LRTB, reading TBLR, and transcription into a 17 x 20 LRTB
3. Alberti cipher with rows 1-6 with key #7, rows 7-14 with key #15, and rows 15-20 with key #7 again

4. Homophonic encoding, with one high count polyphone

55 26 53 22 28 46 12 35 5 27 57 23 24 54 37 22 23
31 47 24 32 48 46 53 22 43 54 25 13 33 29 20 34 23
14 38 21 24 15 20 26 47 1 44 53 22 21 54 9 45 23
22 12 13 56 24 58 20 16 14 43 44 45 59 55 18 17 48
22 22 6 3 40 19 30 18 28 57 31 15 32 29 21 30 33
46 2 41 28 53 23 24 16 29 25 58 22 47 43 48 44 23
17 42 39 19 15 16 22 7 4 10 40 41 11 10 46 45 47
18 48 43 49 12 42 59 22 50 17 5 15 49 37 38 6 51
57 7 50 16 17 5 40 31 24 39 52 41 58 1 51 32 37
15 2 36 6 11 42 13 49 59 20 3 33 35 14 38 40 44
4 39 7 50 16 22 5 46 22 8 41 57 42 37 12 58 17
31 38 6 32 7 5 40 49 33 1 41 39 22 37 6 13 7
50 52 42 10 15 11 3 8 10 59 40 2 31 16 32 11 51
22 14 4 52 1 10 56 5 33 38 41 23 42 6 8 3 49
45 36 4 24 22 22 27 17 55 12 57 39 56 43 30 21 58
50 20 22 21 37 23 20 38 28 29 47 30 39 28 37 13 24
22 26 29 31 30 55 38 32 54 28 56 23 14 44 53 39 24
59 7 21 45 22 23 24 22 22 48 43 57 33 55 46 44 15
12 23 24 29 58 59 30 13 54 53 22 28 47 27 48 40 57
58 20 46 45 9 43 14 29 30 22 25 56 19 54 53 35 16

I still have work to do, and this is preliminary. It only took me 15 tries to generate. All perfect cycles. There should be a bunch of symbols exclusive to rows 1-6 and 15-20.

Here is a better one.

Same cipher, but the message has more comparable cycles 25% randomization.

Rows 1-6 encoded with Alberti row 21, rows 7-14 with Alberti row 1, and rows 15-20 with Alberti row 21.

It wasn’t difficult to make. I think that the spike at P20 is not as difficult to make as I thought it would be because there are bigrams that are different in the differently Alberti encoded parts of the message, but they get Alberti encoded the same.

5 56 20 34 29 3 12 1 30 57 32 20 6 7 27 13 51
30 4 44 52 56 51 5 54 21 54 6 55 28 12 52 27 14
19 51 19 19 20 28 21 7 19 16 50 30 45 17 25 19 5
33 3 54 4 47 18 20 28 16 17 50 28 49 54 3 25 52
6 15 45 50 7 27 55 19 13 29 53 21 19 32 49 54 26
7 31 5 28 55 24 19 18 44 51 25 40 4 50 29 30 12
38 31 42 19 33 48 43 35 19 42 15 30 21 10 18 11 32
17 23 42 19 42 2 23 13 20 33 39 43 18 42 8 13 27
1 38 30 21 19 7 3 41 19 43 34 9 40 32 53 20 39
21 13 33 47 10 48 19 32 16 11 9 19 18 33 45 10 28
2 41 1 30 19 47 11 2 10 15 49 2 42 20 50 2 46
1 19 19 30 9 20 2 5 11 43 8 39 4 1 39 18 9
38 42 39 25 57 19 8 21 43 24 46 9 33 10 40 44 27
2 1 19 20 42 43 5 10 10 42 41 21 26 24 19 34 38
44 29 20 49 18 7 30 3 25 4 3 17 21 31 18 28 19
27 25 44 29 45 26 30 13 14 54 54 44 44 20 31 5 6
45 50 40 4 53 15 5 13 53 54 20 5 24 36 41 25 12
22 16 16 13 55 37 21 28 46 20 19 52 26 24 29 27 3
6 46 51 19 30 2 13 18 20 33 53 17 17 54 7 31 52
45 36 21 18 49 19 50 25 32 19 55 33 13 17 37 36 26

The symbol count distribution is very similar too. And there are 41 spaces occupied by symbols exclusive to rows 1-6 and 15 – 20.

Computed this way, the row-swapped Z340 has about double the average sigma as the unmodified Z340. You can see this looking at individual cycles, where the overall relative probabilities are, on average, less than those of the Z340. Here is the raw output of cycles of both ciphers for comparison:

https://docs.google.com/spreadsheets/d/ … sp=sharing

It shows all L2 cycles detected for both ciphers, side by side, in decreasing order by estimated probability. When you scroll down, you’ll notice an emerging trend for cycles to become more improbable in the row-swapped Z340. Look at the "How much more improbable" column. Positive values indicate an increase in improbability. There are also 172 extra cycles in the row-swapped Z340 compared to the original.

I added L3 cycles to that spreadsheet.

https://docs.google.com/spreadsheets/d/ … sp=sharing

Click on the L=3 tab at the bottom of the spreadsheet. The modified cipher has more improbable cycles than the original, and has about 2,4000 extra cycles that appear (by which I mean cycles that have a minimum run length of 2).

I think it’s interesting that the average statistical significance of individual cycles has gone up for the entire pile of detected cycles. I still have no idea what it means. Maybe it’s just easy to make the cycles behave this way with simple manipulations of the cipher text.

Just a quick rundown, for my measurements, your modified cipher has increased 2, 3-symbol cycles and midpoint shift score while perfect 2, 3, 4-symbol cycles, unigram distance, sliding unigrams, appearance and unique sequences decreased. If some row order needs to be restored a reasonably simple hill climber should do the trick since 20! is not a very large search space for a hill climber with some speed. It will return false positives but at least may hint at what kind of improvements are possible. It would also test your measurement, since if your measurement is too exponential (the whole in the part) the hill climber will come up with silly things.

Deleted.

In the 340 there are very few unigram repeats over short distances, especially when taking in consideration its higher ioc per cipher length than the 408. This is why we see 9 rows which have no repeats, it is not easily connected to transposition after/during encoding and typical encoding randomization.

To show how dramatic this effect is, let’s revisit shuffle tests.
Z408 has 6 rows with no unigram repeats. A test with 10 million shuffles reveals that about 1 in 400 shuffles of Z408 have 6 or more rows with no unigram repeats.
For Z340, only about 1 in 1.5 million shuffles have 9 or more rows which have no repeats.
Pretty strong observation, combined with the unique sequence peak of 26 at length 17 you discovered.

I did another test comparing unigrams in rows and columns. The idea is this:
Take a symbol, then count how many columns it is in. For example, there are three P symbols but they appear in only two columns.
Make these counts for every symbol, then the final measurement is the sum of the counts.

Do the same measurement, but count how many rows the symbols are in instead of columns. Then compare to 1,000,000 shuffles.

The results for Z408 are:
By row: 380. This is 4.5 standard deviations above the mean of shuffles. No shuffle exceeded a score of 379.
By column: 337. This is 0.8 standard deviations above the mean of shuffles. About 1 in 4 shuffles met or exceeded this score.

For Z340:
By row: 322. This is 5.5 standard deviations above the mean of shuffles. No shuffle exceeded a score of 316.
By column: 284. This is 0.5 standard deviations below the mean of shuffles. About 10 in 14 shuffles met or exceeded this score.

So, instances of the same symbol tend to be spread out across rows in Z408 and Z340, and a bit more so for Z340.
They do not show this tendency across columns.

Also, I noticed that some low-frequency symbols seem to repeat along columns, against expectations. I mentioned this here: viewtopic.php?p=55921#p55921
But initial tests suggest it may just be a phantom effect. I still have to confirm this.