A problem with Z408 is that some symbols were repeated early in the cipher. Making it easier to crack.
If you wanted to fix this. You could assign new symbols for each letter as you encode the message. Z may have done this in Z340.
The number of repeated symbols line by line from the top is 0, 2, 8, 13, 9 and so on. Most new symbols are created in the beginning of the cipher.
So we know that already within the first lines there are some symbols that matches the same letter.
He could have created 340 symbols. But I’m guessing he had a target number of symbols or a fixed set of symbols.
If you use this method by creating new symbols along the way. Why would you not create a new symbol for the next letter and repeat one instead?
A reason would be if you had put a cap on how many symbols to use for a letter. Let say that the cap is 4. That would indicate that 3 other symbols before the first time a symbols is repeated is the same letter.
Would it hurt the quality of the cipher if you did something like this?
You could assign new symbols for each letter as you encode the message. Z may have done this in Z340.
I had the same idea a while ago and made a thread about it: viewtopic.php?f=81&t=3604&
Would it hurt the quality of the cipher if you did something like this?
The suppression of frequencies will not be optimal. But we also see that in the 340 and 408.
You could assign new symbols for each letter as you encode the message. Z may have done this in Z340.
I had the same idea a while ago and made a thread about it: http://www.zodiackillersite.com/viewtop … 81&t=3604&
Nice!
What do you think about the other part. If the reason for not creating a new symbol is that there already are enough symbols for that letter. Can that be attacked? The number of symbols that represents the same letter should then be higher among the first symbols that are repeated then on the average. No?
If the reason for not creating a new symbol is that there already are enough symbols for that letter. Can that be attacked?
There are some problems with the hypothesis. For example, why is there only one homophone for the "+" symbol, it repeats 24 times throughout the cipher.
The number of symbols that represents the same letter should then be higher among the first symbols that are repeated then on the average. No?
Yes, because there are more unique symbols at the start of the cipher.
—
The "on the fly" hypothesis has it’s pros and cons.
What you say "Most new symbols are created in the beginning of the cipher." holds true for the 340 and 408 with a greater degree in the 340 if you compare it to the end of the cipher for example (reverse the cipher). One may think that it is normal for sequential homophonic substitution (with predefined key) but it is not.
I ran a experiment with my appearance measurement, it is described in the "on the fly" thread, basically a lower appearance value means that there are more unique symbols at the beginning of a cipher. With a predefined key, perfect cycles and no randomization (1000 ciphers tested) the mean appearance value was 3525, and while including reversing the cipher as last step the value is 3537. So there was no real difference between the beginning and the end of the ciphers in that regard.
Though it can happen "by accident" if the letter frequencies in the beginning of the cipher are better correlated with the predefined key than the letter frequencies at the end of the cipher. The chance of it happening in the 340 is 0.95% (with the assumption of 25% cycle randomization). And the chance of it happening in the 408 is 54.55% (generalizing the encoding randomness in the 408 to 15% which matches the 2-symbol cycle scores).
Takeaway is that it seems a significant observation in the 340 but I am not sure if it is attributable to a "on the fly" hypothesis because of other problems but there may be some truth in it.
This behavior also occurs when encrypting random plaintext. Here is an example:
– Repeat the sequence "ABCDEFGHIJKLM" all the time. You get the following "Cipher":
ABCDEFGHIJKLMABCD EFGHIJKLMABCDEFGH IJKLMABCDEFGHIJKL MABCDEFGHIJKLMABC DEFGHIJKLMABCDEFG HIJKLMABCDEFGHIJK LMABCDEFGHIJKLMAB CDEFGHIJKLMABCDEF GHIJKLMABCDEFGHIJ KLMABCDEFGHIJKLMA BCDEFGHIJKLMABCDE FGHIJKLMABCDEFGHI JKLMABCDEFGHIJKLM ABCDEFGHIJKLMABCD EFGHIJKLMABCDEFGH IJKLMABCDEFGHIJKL MABCDEFGHIJKLMABC DEFGHIJKLMABCDEFG HIJKLMABCDEFGHIJK LMABCDEFGHIJKLMAB
– Now shuffle this cipher. Like this:
EGMBDBCELKGBCLCIM BGFLHHMMGFBDBAIHJ KLDBEIAADMAFGJMLK GIFFACDFEMEFMBMHH DJEMIKEIKJCGCKGEH ADJJKIEJIBDBDEHCH KIKMJBBJFJFJFGBEK EMHMKAEHGBGJFAKMJ EHCKLIAHGIEGHAFCD ABFLBJFMIJDMCFIDE CBILLMCKLDFMCGEFA KDLGAEIBAJALKCHEI CIAIHLEGELBDCJJHE LCBLCALLBAKBGBAKH GFFCIKLHDDKAKEHDJ MFCCAAMKFBFHHMCCG EJHGHGGELBJCGKGHD ICFMMGFBDMJKIALLH CDABAAIAFJLMGKDEF IDJDDJIJLHMLIKDIL
Now apply a homophonic substitution with slight random cycles:
Key:
dDiZ94bekBHax3y+0PgIEJF2phcC5mj:uU;Aq7RX=YOnGVto1KMLwsNrvSQl-TW AAAAABBCCDDDEEEEEGGHHHIIIIJKLLLMAAABBCCDDDEEEEEFGGHHHIIIIJKLLLM
Final cipher:
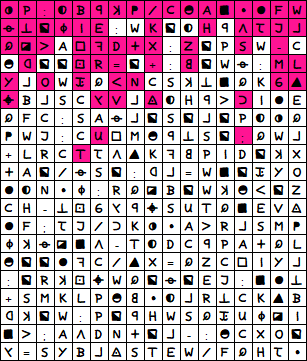
xP:4Bbe35CgAkm7FW q1ojIE:WKo4Hbd2Jc QlaAypDiX:ZoPSW-C ghoo9R=o+:0oWq:ML YcOWsQnNCSe1kQKGw uBcSCrVcv4HbatI7E QFC:SAqcoSocoP4xQ 3WJ:CUyMgb1So;QWc +LRCT2dwKp0PIDoeX iAo5qSo:hc=WkosYO 74Nmj:RQlBoWegnoZ CH-19GrbuSUTQkEVv 7F;2J5tKxmAaRcSM3 jeqlkd-T4DCbPAiQL goo7pC5wX=QZCyIYc :oRe9uWQoqoEJ:k71 +SMKLPg0m4cR1CKwB heoW:PobHWSQsUjlI ka;AdDNioc-:gCXOo r=SYBcvSTEW5FQH2m
In plain text, each letter appears with the same frequency. Since the key doesn’t take this into account, you get a quite good fake-cipher. It shows a similar behavior as z340 in many things.
– Raw IOC: 2464
– Appearance: 2792
– 22 bigrams, 1 trigram
– Bigram peak at P8 (37)
– One symbol that occurs unusually often (half filled square)
On the other hand, there are also points where my example differs from z340. For example, my test "deceptive periods" shows that there is no really "clean" period behavior. Unique sequence length is also much smaller than in z340.
However, if the fake cipher is not created by shuffling, but by a certain scheme or system, then the remaining features of z340 may also show up. Let’s see, maybe I’ll find time and energy to try out some new hoax schemes and test them against all known z340 phenomena.
This behavior also occurs when encrypting random plaintext.
Thanks for jumping in Largo, I had compiled some additional information but lost my post.
Takeaway:
Your "ABCDEFGHIJKLM" sequence ciphers have a lower than usual appearance on average versus using normal plain texts mostly because of there only being 13 letters and in smaller part to it having a flat frequency distribution. Though reversing the cipher does not change the appearance much in both cases and the reversed 340 has a higher appearance. That could of course be a coincidence in the 340.
I like your deceptive periods test and it is interesting how the frequency profile affects the measurements. Is there a profile that fits the unique sequence length better? That is however another matter.
This behavior also occurs when encrypting random plaintext. Here is an example:
Another thing that got me thinking about the "on the fly" theory is that the shortest substring of the Z340 that contains all symbols starts at the beginning of the cipher (position 2). In this random cipher it starts somewhere in the middle (position 126?). As aspected?
This behavior also occurs when encrypting random plaintext. Here is an example:
Another thing that got me thinking about the "on the fly" theory is that the shortest substring of the Z340 that contains all symbols starts at the beginning of the cipher (position 2). In this random cipher it starts somewhere in the middle (position 126?). As aspected?
Yes, expected for the random cipher since it has no mechanism in place that would bias more unique symbols to the top of the cipher. If the 340 is a sequential homophonic like the 408 (with more randomization in its cycles) with a predefined key then there is a 1% chance that the symbols would appear so early. With the 408 the chance is 54% so it jives with having a predefined key. In other words it looks like the 408 has a predefined key while the 340 has not.
I will take a look into your idea of finding the shortest sub string that contains all symbols to see if it can further corroborate the findings.
I will take a look into your idea of finding the shortest sub string that contains all symbols to see if it can further corroborate the findings.
It does, for 10,000 sequential homophonic ciphers (various english plain text, 25% random cycles) the chance of having the shortest sub string that contains all symbols at position 2 or earlier is about 4%.
In the 408, the shortest substring that contains all symbols is at position 145.
Why does the 340 does have so many seemingly non-random odd properties?
I will take a look into your idea of finding the shortest sub string that contains all symbols to see if it can further corroborate the findings.
It does, for 10,000 sequential homophonic ciphers (various english plain text, 25% random cycles) the chance of having the shortest sub string that contains all symbols at position 2 or earlier is about 4%.
In the 408, the shortest substring that contains all symbols is at position 145.
Why does the 340 does have so many seemingly non-random odd properties?
Is it 25% from beginning to end, or do the cycles become increasingly random from perfect at the beginning?
Is it 25% from beginning to end, or do the cycles become increasingly random from perfect at the beginning?
From beginning to end.
Are you suggesting that the increasingly random cycles could be a mechanic for the observations? I had not thought of that and agree that it could be something. Needs testing.
Here is my thread about increasingly random cycles in the 340 and 408: viewtopic.php?f=81&t=4099
Yes, maybe, because if he started with perfect cycles, then he would be sure to pack all of the symbols in the shortest possible all-symbol substring toward the beginning. Random symbol selection would just make the all-symbol substrings longer, so there is a relationship between randomization and the lengths and positions of the all-symbol substrings.
Are you suggesting that the increasingly random cycles could be a mechanic for the observations? I had not thought of that and agree that it could be something. Needs testing.
So I am testing increasingly random cycles, from 0% at the start of the cipher to 75% at the end of the cipher progressing linearly. The average appearance score was 3537, and with the cipher reversed it was 4225 so this is indeed a possible mechanic. Good thinking smokie. The appearance score of the 340 is still quite low, even with the 0% to 75% the chance is still only 4.55% of it being so low, it did come up from about 1% though.
Here follows a cipher with 0-75% increasingly random cycles, I noticed that the appearance score is subject to the appearance score of the plain text, I rolled quite a few times to get something in the 340 ball park. Shortest sub string that contains all symbols is at position 10.
?)"WBPV7&>$@L95R =%I'2C4UM4;[.8+0E )^L_N!G3WE,XH;6(R E-P:[8QL+@$1O<;%[ 274*5/8,&W4K#MI. G=V)'%BWHX%E$PL_R ^7G3:54AXRD1.4*_S N%V8W4F!GYT0:7OU) 4J%L<54IW3PR4W42O !G';"Q^@7NR(?".9, NS@Y14VT;%<4D):_ 4KWT6#P*]@A[IN=!& 8+/24F,4ZD*0LSQY ;+")TMH49!4.;V_4I 1J@Y[+@D9,N/MT)4 :PD'RSSH:1048L!?W 3Y%4;L")N<XH4CQ/% &,4QTH[6TM]7TL,;< DQG3MWT4*L+!>@;+ %[8"MS#R2LI5N5G=K 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 24 27 28 29 30 31 32 33 2 34 13 35 36 37 38 39 4 33 40 41 42 27 43 44 17 33 45 6 46 28 30 47 13 31 12 11 48 49 50 27 19 28 22 8 24 51 16 52 30 40 9 14 4 24 53 54 26 20 29 38 18 7 2 21 19 5 4 42 41 19 33 11 6 13 35 17 34 8 38 39 46 16 24 55 41 17 56 48 29 24 51 35 57 36 19 7 30 4 24 58 37 38 59 60 32 46 8 49 25 2 24 61 19 13 50 16 24 20 4 39 6 17 24 4 24 22 49 37 38 21 27 3 47 34 12 8 36 17 44 1 3 29 15 40 36 57 12 59 48 24 7 14 60 27 19 50 24 56 2 46 35 24 53 4 60 43 54 6 51 62 12 55 28 20 36 18 37 9 30 31 14 52 22 24 58 40 24 63 56 51 32 13 57 47 59 27 31 3 2 60 26 42 24 15 37 24 29 27 7 35 24 20 48 61 12 59 28 31 12 56 14 15 40 36 52 26 60 2 24 46 6 56 21 17 57 57 42 46 48 32 24 30 13 37 1 4 39 59 19 24 27 13 3 2 36 50 41 42 24 23 47 52 19 9 40 24 47 60 42 28 43 60 26 62 8 60 13 40 27 50 56 47 38 39 26 4 60 24 14 51 13 31 37 10 12 27 31 19 28 30 3 26 57 54 17 22 13 20 16 36 16 38 18 53 WEHAVECOMPLETEDOU RASSIGNMENTTOTHEB ESTOFOURABILITYSU BJECTTOTHELIMITAT IONSOFTIMEANDRESO URCESAVAILABLETOU SOURCONCLUSIONSOF FACTANDOURRECOMME NDATIONSAREUNANIM OUSTHOSEOFUSWHODI FFERINCERTAINSECO NDARYRESPECTSFROM THEFINDINGSSETFOR THHEREINDONOTCONS IDERTHESEDIFFEREN CESSUFFICIENTTOWA RRANTTHEFILINGOFA MINORITYREPORTITI SOUREARNESTHOPETH ATTHEFRUITSOFOURD
4.55% is still pretty low.
EDIT: But what if you just make sure to introduce every symbol in the beginning by using a perfect cycle, then increase the randomness.
You could do this one of two ways:
1. Each individual homophone group would have to be perfect before randomness could occur within its group. All groups start out perfect, then one by one the become increasingly random once they are perfect.
2. Or, just make sure to introduce each symbol with perfect cycles, and then start to increase randomness for all groups at the same time after all symbols are introduced.
EDIT: But what if you just make sure to introduce every symbol in the beginning by using a perfect cycle, then increase the randomness
With perfect cycles all the way through the chance is 7.95% of the appearance score being so low in the 340.
To get the average appearance score around 2924 (that of the 340) I need to drop the raw ioc target to 1800 while the 340 has a raw ioc of 2236. And that is without any randomness in the cycles.
I will try to match the frequency profile of the 340 as closely as possible and see if that changes things.