Hello All,
Although the following for now is inconclusive I post it here for completeness and perhaps as a reference point for any future research.
General.
The Kasiski examination is a slide comparison where the Cipher text is repeatedly compared to it self with an incremental offset.
This is also sometimes referred to as a slide attack. This method is usually used to extract key lengths in Polyalphabetic ciphers such as Vigenere Cipher etc.
a count value per shift is the usual output and can be column graphed for visual interpretation. for example a key lengths of 10 would be seen as spikes above the average every 10th multiple of stride however due to cipher text distribution spikes sometimes be reduced/hidden at some locations and only present others I.e not be present <90 but at 100,110,120,130 etc.
Z340
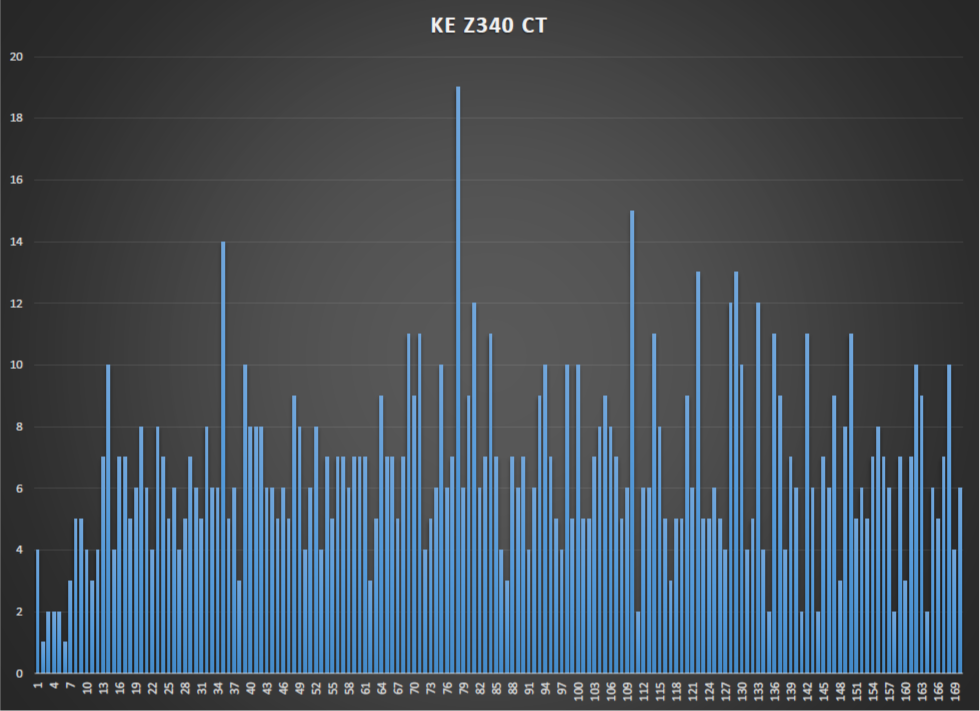
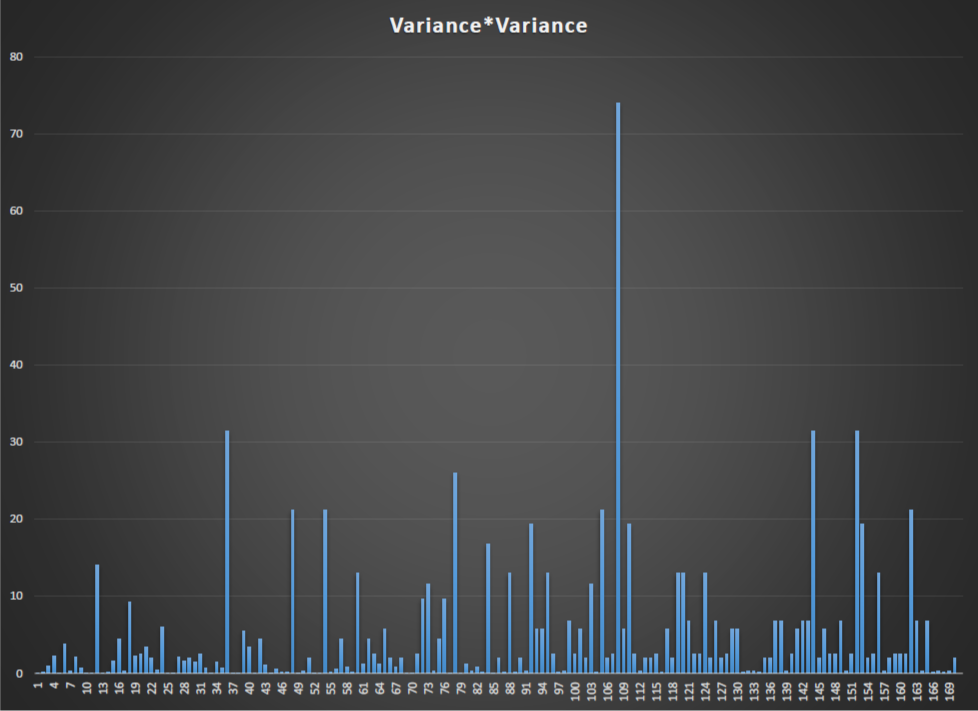
By doing the same on Z340 a Spike was noted at a shift of 78 and a slight above average at 39 (78/2) with no noticeable harmonic at 156 (2*78).
Out of interest I applied the Key from 408 to 340 and noted a still present spike at 78 and some increase in noise was noted which is to be expected.
A Mod/position/stride transposition was calculated from 1 (none) to 339. at a stride of 2 (1,3,5,etc) a spike was noted at 39 (78/2) and at position 3 a spike was noted at 26 (78/3) and so on and this expected as the data has been effectively re-sampled.
The only relationship i can find to Z340/Z408 with the KE spike @ 78 (or factors) is Z408 – 18 (padding) = 390/5 = 78 which could imply a chunk of 408 was used as a poly key for Z340. I still find that is very unlikely however it needs to be raised.
Personally i feel the data is inconclusive and suspect that the Spike is more a artifact of the Homophonic symbol cycling.
I would be interested what other thought of the topic.
Regards
Bart
The Kasiski examination is a slide comparison where the Cipher text is repeatedly compared to it self with an incremental offset. This is also sometimes referred to as a slide attack. This method is usually used to extract key lengths in Polyalphabetic ciphers such as Vigenere Cipher etc.
Do you mean what is described as coincidence counting here: https://en.wikipedia.org/wiki/Kasiski_examination ?
Let’s say we transcribed the 340 into 78 columns, summed the repeating ciphertext in each column, and then divided that sum by the number of rows. Would we see a spike when compared to drafting the message into any other number of columns? Or would that be a different analysis?
By doing the same on Z340 a Spike was noted at a shift of 78 and a slight above average at 39 (78/2) with no noticeable harmonic at 156 (2*78).
What do you think about the y-value of the spike? Is it statistically improbable for a cipher with one homophonic substitution key of 63 ciphertext and an English plaintext? If you made some messages with plaintext randomly selected from some source, and with keys of 63 ciphertext and varying diffusion efficiency, how easy or difficult would it be to replicate the spike, or find spikes with even higher y-values?
Are the ciphertext repeats found in your slide analysis coming more from a particular area of the message ( e.g. positions 1-170 versus positions 171-340 ), or are they uniformly distributed?
What if you did the slide analysis in different directions?
Out of interest I applied the Key from 408 to 340 and noted a still present spike at 78 and some increase in noise was noted which is to be expected.
I don’t understand. You applied the 408 key ( and not the plaintext ) to the 340, which converted the 340 into a new message ( rather than solving the 340 ), applied the slide comparison, and again found a spike at 78?
A Mod/position/stride transposition was calculated from 1 (none) to 339. at a stride of 2 (1,3,5,etc) a spike was noted at 39 (78/2) and at position 3 a spike was noted at 26 (78/3) and so on and this expected as the data has been effectively re-sampled.
Can you please show me a link or describe a mod/position/stride transposition? Can you go into a little more detail here, taking into account different audiences? I am very interested in all of the above but don’t always understand what people are talking about.
There are a lot of period 19 ( or period 18 as described by Practical Cryptography ) bigram repeats. But there are are more period 39 bigram repeats than period 38 bigram repeats. Also, the pivot symbols are offset by 39 positions. I wonder if there is any connection.
Thanks.
The Kasiski examination is a slide comparison where the Cipher text is repeatedly compared to it self with an incremental offset. This is also sometimes referred to as a slide attack. This method is usually used to extract key lengths in Polyalphabetic ciphers such as Vigenere Cipher etc.
Do you mean what is described as coincidence counting here: https://en.wikipedia.org/wiki/Kasiski_examination ?
Yes it is the same. Here is the code for my implementation.
#include <stdio.h>
#include <string.h>
unsigned char input[]="HER>pl^VPk|1LTG2dNp+B(#O%DWY.<*Kf)By:cM+UZGW()L#zHJSpp7^l8*V3pO++RK2_9M+ztjd|5FP+&4k/p8R^FlO-*dCkF>2D(#5+Kq%;2UcXGV.zL|(G2Jfj#O+_NYz+@L9d<M+b+ZR2FBcyA64K-zlUV+^J+Op7<FBy-U+R/5tE|DYBpbTMKO2<clRJ|*5T4M.+&BFz69Sy#+N|5FBc(;8RlGFN^f524b.cV4t++yBX1*:49CE>VUZ5-+|c.3zBK(Op^.fMqG2RcT+L16C<+FlWB|)L++)WCzWcPOSHT/()p|FkdW<7tB_YOB*-Cc>MDHNpkSzZO8A|K;+";
//************************************************************************************************************************
void main (void)
{
unsigned int index,count,length,offset;
length = strlen(input);
for (offset = 1 ; offset < length ; offset++)
{
count = 0;
for (index = 0 ; index < length ; index++)
{
if ((input[index] == input[(index+offset)%length]))
count++;
}
printf("%u,%un",offset,count);
}
}
Let’s say we transcribed the 340 into 78 columns, summed the repeating ciphertext in each column, and then divided that sum by the number of rows. Would we see a spike when compared to drafting the message into any other number of columns? Or would that be a different analysis?
Short of trying it I believe what you propose is different. However your description reminds me of another key length finding method that uses columns.
In this method you calculate the IoC of each column and on a Column size == Keylength all the IoCs are the closest.
By doing the same on Z340 a Spike was noted at a shift of 78 and a slight above average at 39 (78/2) with no noticeable harmonic at 156 (2*78).
What do you think about the y-value of the spike?
I don’t know. It is over 3 * the mean from memory which is some what significant and has a reasonable SNR(signal to noise) but this is also the first time i have encountered a Homophonic cipher so I do not have a full appreciation for the interaction of the higher symbol space. Also the lack of sub/harmonics lowers my confidence in its validity.
Is it statistically improbable for a cipher with one homophonic substitution key of 63 ciphertext and an English plaintext?
No, I don’t think it is, however my stats math is very rusty and has been causing me some annoyance lately. I have been tempted to do a refresher on it.
If you made some messages with plaintext randomly selected from some source, and with keys of 63 ciphertext and varying diffusion efficiency, how easy or difficult would it be to replicate the spike, or find spikes with even higher y-values?
As we all know this purely comes down to the PT word and key choice. short of running an experiment which i am not setup for i don’t know.
Are the ciphertext repeats found in your slide analysis coming more from a particular area of the message ( e.g. positions 1-170 versus positions 171-340 ), or are they uniformly distributed?
Take a look for yourself
Shift = 078 ................d ................. ........G....#... ............+.R.. ............+.... p..............D. .......2.c....... .............+... .........F.....4. .....+........... ....5..|......... .........T....... ................. ..............t.. ................. ................. .........+....... ................. ................. .................
What if you did the slide analysis in different directions?
As the process wraps over itself the process is symmetrical.
Out of interest I applied the Key from 408 to 340 and noted a still present spike at 78 and some increase in noise was noted which is to be expected.
I don’t understand. You applied the 408 key ( and not the plaintext ) to the 340, which converted the 340 into a new message ( rather than solving the 340 ), applied the slide comparison, and again found a spike at 78?
Yes this is a bit of a WTF moment I agree. however I wanted to compress my symbol space from 63 to <=26 so instead of making up random data I decided just to apply the Key from Z408 to Z340. The underling homophonic code will still show the same attributes at 78 but i was more interested in what was happening post substitution if that makes any sense?
A Mod/position/stride transposition was calculated from 1 (none) to 339. at a stride of 2 (1,3,5,etc) a spike was noted at 39 (78/2) and at position 3 a spike was noted at 26 (78/3) and so on and this expected as the data has been effectively re-sampled.
Can you please show me a link or describe a mod/position/stride transposition? Can you go into a little more detail here, taking into account different audiences? I am very interested in all of the above but don’t always understand what people are talking about.
Hmmm, By stride i mean the following
for the text string "ABCDEFGHIJK"
A stride of 2 would be "ACEGIKBDFHJ"
A Stride of 3 would be "ADGJBEHKCFI"
Hopefully that makes sense and i didn’t stuff it up.
There are a lot of period 19 ( or period 18 as described by Practical Cryptography ) bigram repeats. But there are are more period 39 bigram repeats than period 38 bigram repeats. Also, the pivot symbols are offset by 39 positions. I wonder if there is any connection.
Thanks.
That is a very interesting point and i am kicking my self for not remembering that the pivots are 39 after counting them out last week.
Here are the hits on 19 and 39. nothing exceptional stands out. keep in mind this is just an offset comparison not a period/stride.
Thanks for taking the time to look over this and comment.
Regards
Bart
Shift = 019 ................. ................. ................. ................. .......d..F...... ................. ................. ................. ...+............. ................. ..R.............. ......|.......... ................. ................. ................. ................. ................. .........O....... ................. ................. Shift = 039 ................. ......O.......... ................. ...............K. ................. ................. ................. .............+... ................. ........+........ .+..5............ ................. ..9......5....... ...............+. ................. ................. ................. ................p ................. .................
Bart,
Thank you very much for answering my questions. I will try to do the slide analysis myself. Sometimes I have to work through a concept myself to understand and consider it. Even it it is relatively simple.
1. What different ciphers do you know of that create detectable periods? I already have route transposition, bifid, and vigenere on my list.
2. What about ciphers that have detectable harmonic periods? Detectable periods that are divisors or multiples of other periods, right? I have route transposition on my list.
3. What about where a detectable divisor or multiple is shifted by one position? For example, 15 and 29 instead of 15 and 30? Say, for instance, a cipher that encodes multiple units of plaintext of the same size but where the chosen unit size creates the one position shift that I am describing.
Bifid with an even plaintext period is easy to detect, but with an odd plaintext period is difficult to detect. I mean, something sort of similar but that creates a detectable harmonic shift. Maybe one that is detectable uniformly throughout the message, or maybe one that creates the harmonic shift in one part of the message but not the other part.
Thanks.
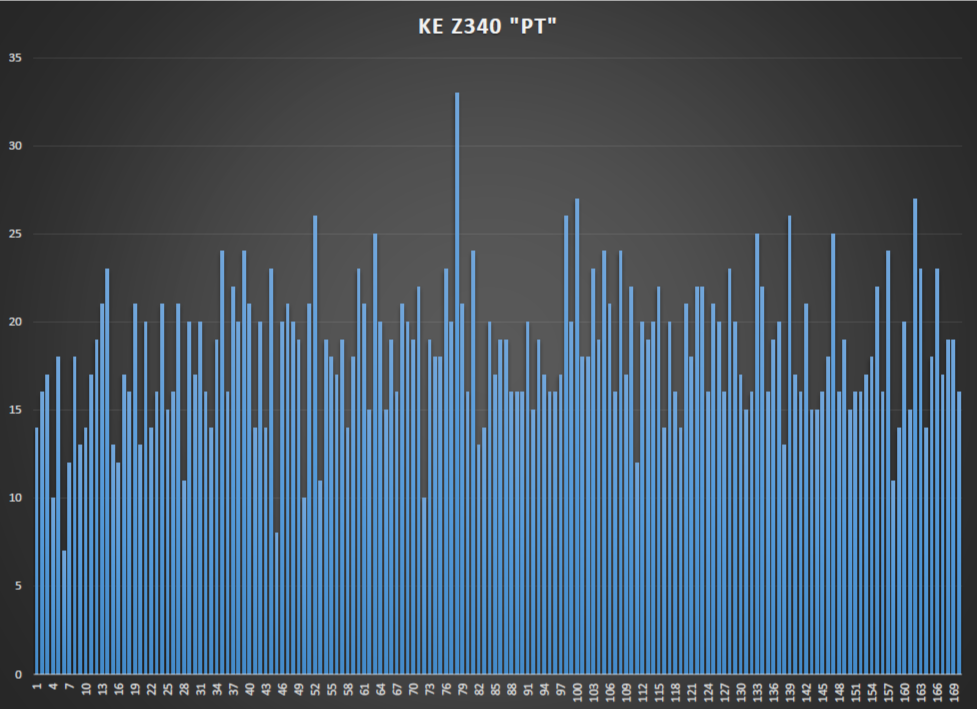
Bart, I did my own coincidence counting. I found the spike at 78. But for some reason my y-values are not as high as yours. I found out that I only needed to work with positions 1-170, and add up to 170 for my position slide. Otherwise I just got a column chart that was a mirror image of itself. Here is my chart, which is EDIT: ( sort of ) similar to yours.
I random shuffled the message 100 times and could not get a spike as high as 19 count. I didn’t even get 18 or 17. But I did get 16 quite a few times. I am going to continue to explore your findings a little bit more.
EDIT: I used a spreadsheet. For x=1, I compared position 1 with position 2, position 3 with position 4, etc. For x=2, I compared position 1 with position 3, position 2 with position 4, etc. For x=78, I compared position 1 with position 79, position 2 with position 80, etc. I have two other spikes at x=35 and x=110. So although my chart has a spike at x=78, like yours, my chart is still different than yours. I don’t understand why.
Bart,
Thank you very much for answering my questions. I will try to do the slide analysis myself. Sometimes I have to work through a concept myself to understand and consider it. Even it it is relatively simple.
Hi Smokie,
Yes I am the same ![]()
1. What different ciphers do you know of that create detectable periods? I already have route transposition, bifid, and vigenere on my list.
2. What about ciphers that have detectable harmonic periods? Detectable periods that are divisors or multiples of other periods, right? I have route transposition on my list.
3. What about where a detectable divisor or multiple is shifted by one position? For example, 15 and 29 instead of 15 and 30? Say, for instance, a cipher that encodes multiple units of plaintext of the same size but where the chosen unit size creates the one position shift that I am describing.
Bifid with an even plaintext period is easy to detect, but with an odd plaintext period is difficult to detect. I mean, something sort of similar but that creates a detectable harmonic shift. Maybe one that is detectable uniformly throughout the message, or maybe one that creates the harmonic shift in one part of the message but not the other part.
Thanks.
Unfortunately My Cipher work has been focused at select ciphers and only of late have I been venturing out and looking at other forms.
Most of my work has been on Vigenere ciphers in particular around the Kryptos sculpture and more than I care for on substitution ciphers in the form of cryptograms etc.
So sorry I can not add to the list.
Currently I am looking into ciphers such as playfair and other keygrid based ciphers.
I assume this has been kicked around before but I noticed the other night that symbol space for Z340 and Z408 are divisible by 9
I.e.
9×7 = 63 Z340
9×6 = 54 Z408
Just for inclusion 7 symbols were dropped from Z408 and 16 were added for a net gain of 9 in Z340.
I have done some work on IoC block searches which DOranchak has been privy to but I would like to get back this soon to validate and optimize my process
before seeing if i can find any correlation to KE results or anything new.
Regards
Bart
My coincidence counting spreadsheet seems to be working, and I see what you mean by "harmonics."
I made a 340 ciphertext message with the first 340 plaintext from the 408. First, I used a Vigenere cipher with the keyword ALPHABETSOUP, which is twelve letters. Then I encoded the message again with an efficiently diffusing homophonic key with 57 symbols. I didn’t cycle the homophonic ciphertext groups perfectly. Instead, I chose ciphertext from them at random 25% of the time.
20 45 50 34 10 24 26 11 8 46 18 43 31 32 9 45 25
13 14 51 42 29 30 19 12 38 21 31 36 39 36 15 27 33
6 42 42 55 50 1 20 40 33 19 22 37 57 22 28 10 48
19 28 24 27 11 8 47 18 44 45 40 2 23 16 6 33 53
3 5 28 47 12 33 9 56 34 13 48 27 41 35 48 32 42
9 39 40 4 29 26 25 24 44 55 6 30 8 21 23 1 29
23 54 22 7 30 19 2 56 50 41 2 27 36 55 37 57 14
20 29 44 50 35 25 39 36 15 49 18 6 52 28 34 44 31
43 13 45 13 46 19 6 39 26 57 18 2 40 21 43 5 8
57 7 7 17 32 27 47 10 37 20 16 42 36 7 20 21 9
39 7 12 30 15 54 24 19 56 16 38 36 31 42 16 13 54
26 3 6 3 28 29 14 16 55 29 8 29 25 16 39 57 24
21 11 48 19 17 22 44 10 25 43 56 33 11 9 20 49 3
35 50 19 52 48 28 50 35 12 47 18 40 53 24 54 15 47
50 51 10 38 25 32 24 27 14 51 22 37 44 8 34 55 54
42 31 5 44 38 44 48 49 38 4 56 37 18 25 26 54 1
46 49 6 32 43 31 57 32 24 27 20 47 30 48 15 2 5
31 34 44 26 15 33 34 23 57 42 23 11 9 50 9 20 27
32 16 17 18 3 51 44 31 28 44 42 28 7 16 35 4 55
33 12 28 32 6 36 13 7 19 26 23 7 1 25 12 17 14
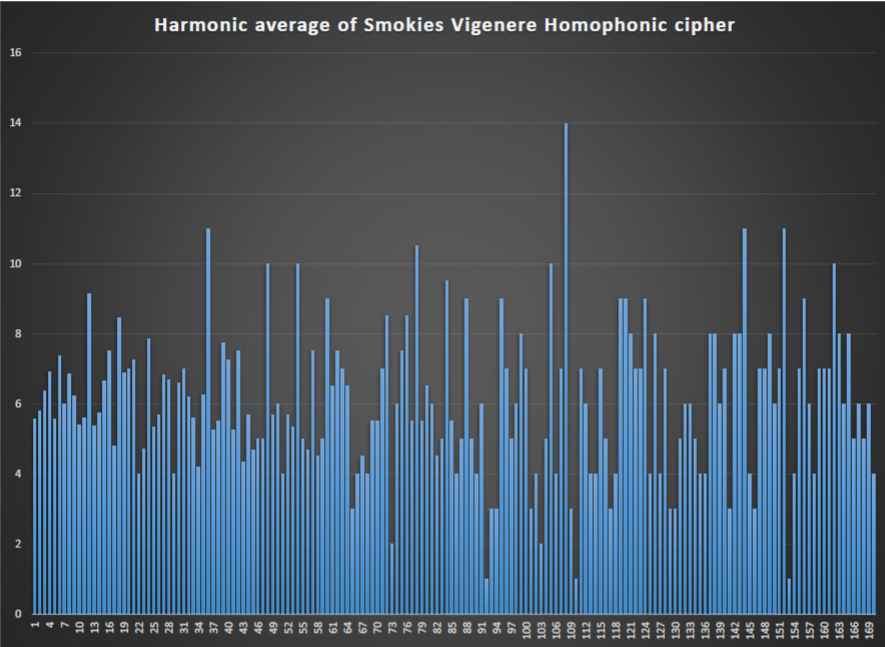
I didn’t get a spike at 12, but I did get spikes at 36, 48, 84 and 108. All multiples of 12. None were as high as the spikes at 35, 78 and 110 that I found with the 340.
What I find sort of interesting is that with the 340, the results for x=2 through 6 are all very low values and clustered together.
Very interesting Smokie.
Are you able to share the individual data sets?
Pt, Ct vigenere & Ct monophonic.
I have a couple of experiments i want to try l tonight
Regards
Bart
Very interesting Smokie.
Are you able to share the individual data sets?
Pt, Ct vigenere & Ct monophonic.
I have a couple of experiments i want to try l tonight
Regards
Bart
I L I K E K I L L I N G P E O P L
E B E C A U S E I T I S S O M U C
H F U N I T I S M O R E F U N T H
A N K I L L I N G W I L D G A M E
I N T H E F O R R E S T B E C A U
S E M A N I S T H E M O S T D A N
G E R O U S A N I M A L O F A L L
T O K I L L S O M E T H I N G G I
V E S M E T H E M O S T T H R I L
L I N G E X P E R E N C E I T I S
E V E N B E T T E R T H A N G E T
T I N G Y O U R R O C K S O F F W
I T H A G I R L T H E B E S T P A
R T O F I T I S T H A T W H E N I
D I E I W I L L B E R E B O R N I
N P A R A D I C E A N D A L L T H
E I H A V E K I L L E D W I L L B
E C O M E M Y S L A V E S I W I L
L N O T G I V E Y O U M Y N A M E
B E C A U S E Y O U W I L L T R Y
ALPHABETSOUP
I W X R E L M E D W H V P P D W L
F F X U O O H E T I P S T S F M Q
B U U Y X A I T Q H J S Z J N E W
H N L M E D W H V W T A K G B Q X
A B N W E Q D Y R F W M T S W P U
D T T A O M L L V Y B O D I K A O
K X J C O H A Y X T A M S Y S Z F
I O V X S L T S F W H B X N R V P
V F W F W H B T M Z H A T I V B D
Z C C G P M W E S I G U S C I I D
T C E O F X L H Y G T S P U G F X
M A B A N O F G Y O D O L G T Z L
I E W H G J V E L V Y Q E D I W A
S X H X W N X S E W H T X L X F W
X X E T L P L M F X J S V D R Y X
U P B V T V W W T A Y S H L M X A
W W B P V P Z P L M I W O W F A B
P R V M F Q R K Z U K E D X D I M
P G G H A X V P N V U N C G S A Y
Q E N P B S F C H M K C A L E G F
And I am pretty sure that this is the key. I didn’t save it, but used the same settings to re-create it. So it should be correct.
A 1 2 3 4
B 5 6
C 7
D 8 9
E 10 11 12
F 13 14 15
G 16 17
H 18 19
I 20 21
J 22
K 23
L 24 25
M 26 27
N 28
O 29 30
P 31 32
Q 33
R 34
S 35 36 37
T 38 39 40 41
U 42
V 43 44
W 45 46 47 48 49
X 50 51 52 53 54
Y 55 56
Z 57
I will continue looking at this tonight or in the next couple of days.
Bart,
I made 100 messages randomly selected from the plaintext library found here:
They are not Vigenere messages. Just homophonic substitution. I made the keys so that they would diffuse the plaintext inefficiently, so as to increase coincidence counting values. In other words, I made keys that look like this with a slightly higher count of ciphertext mapping to low frequency plaintext, and slightly lower count of ciphertext mapping to high frequency plaintext.
A 1 2 3 4
B 5
C 6 7 8
D 9 10
E 11 12 13 14 15
F 16 17
G 18 19
H 20 21 22 23
I 24 25 26 27
J 28
K 29
L 30 31 32
M 33 34
N 35 36 37 38
O 39 40 41 42
P 43 44
Q
R 45 46 47
S 48 49 50
T 51 52 53 54 55
U 56 57
V 58
W 59 60
X 61
Y 62
Z 63
Instead of keys that look like this and have fewer ciphertext mapping to low frequency plaintext and more ciphertext mapping to high frequency plaintext.
A 1 2 3
B 4
C 5 6
D 7 8
E 9 10 11 12 13 14 15 16
F 17
G 18
H 19 20 21
I 22 23 24 25 26
J 27
K 28
L 29 30 31
M 32
N 33 34 35 36
O 37 38 39 40
P 41
Q
R 42 43 44
S 45 46 47
T 48 49 50 51 52 53 54 55
U 56 57
V 58
W 59 60
X 61
Y 62
Z 63
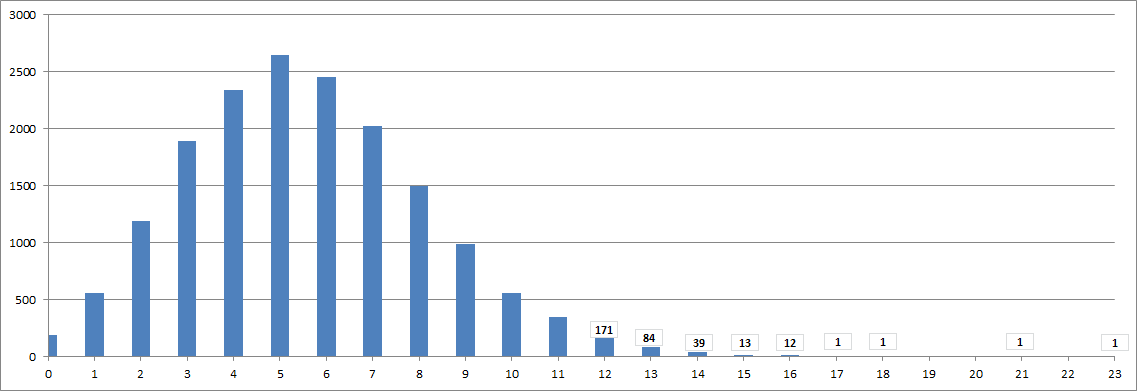
Then I randomized my homophonic symbol selection at 25% as with the message above to roughly approximate the 340 cycles. I saved all of the results for x=1 to x=170 for the 100 messages, and tallied them. Below is a column chart of the tallies, with y values written in where they did not show on the chart. There were four messages with y values of 17 or above, and two with y values over 19 ( my y value for x=78 for the 340 is 19 ).
So maybe coincidence counting detects something else besides just the period for a Vigenere cipher? Maybe there is roughly less than 5% chance of making a homophonic substitution message with a spike that you detected, and that is what we are looking at? Please stay on the message board. We don’t have enough programmer cryptanalysts working on the 340. I am not one. I am just a person with a small laptop, Excel and a hobby.
I will use my coincidence counting spreadsheet to look at transcription from all four corners and two directions from each corner. Then I will show the unigram repeats at period 78 compared to other similar period stats.
Are you aware of the "prime phobia" phenomenon? You would probably be interested in this thread:
Smokie, Looks like you been up to some good work.
I made 100 messages randomly selected from the plaintext library found here:
http://zodiackillersite.com/viewtopic.php?f=81&t=2435They are not Vigenere messages. Just homophonic substitution. I made the keys so that they would diffuse the plaintext inefficiently, so as to increase coincidence counting values. In other words, I made keys that look like this with a slightly higher count of ciphertext mapping to low frequency plaintext, and slightly lower count of ciphertext mapping to high frequency plaintext.
Ok walk me through this…
you generated 100 random messages.
you homophonicly keyed them with 63 symbol space
but can you please define "diffuse the plaintext inefficiently" i don’t understand this.
Then I randomized my homophonic symbol selection at 25% as with the message above to roughly approximate the 340 cycles.
I saved all of the results for x=1 to x=170 for the 100 messages, and tallied them.
Below is a column chart of the tallies, with y values written in where they did not show on the chart.
There were four messages with y values of 17 or above, and two with y values over 19 ( my y value for x=78 for the 340 is 19 ).
Ok so just check me here.
You tallied up all the Shift78 across all the messages.
The average spread expected would be 340/63 ~ 5.4 which is what appears you have with a vaguely standard bell curve.
This would mean that the peak of the coincidence counting has moved position between messages.
Hmmm… I wonder if we have a frequency mixing going on…
if you mix (two or more) signals together F1 and F2 then depending on the operation you will get Fout = F1+F2, F1*F2 and every mix and combo imaginable.
I wonder if we are seeing Fout and that we have the Letter frequency and symbol frequency beating together.
This is complicated more by the fact that neither is linear.
So maybe coincidence counting detects something else besides just the period for a Vigenere cipher? Maybe there is roughly less than 5% chance of making a homophonic substitution message with a spike that you detected, and that is what we are looking at?
Yes i think my previous comment of the mixing is likely.
I guess in this case we just Keep the coincidence count of 78 as a known quirk which may come in handy in the future.
Please stay on the message board.
We don’t have enough programmer cryptanalysts working on the 340.
I am not one. I am just a person with a small laptop, Excel and a hobby.
You guys are doing pretty well compared to some groups and You a pretty wicked with the Excel then ![]()
I intended to stick around but like most have limited availability due to work and family life.
In my job i am a hardware engineer but do some programming for hardware bring up and i have only been doing crypto for a short while so i still have plenty learning to go.
I will use my coincidence counting spreadsheet to look at transcription from all four corners and two directions from each corner. Then I will show the unigram repeats at period 78 compared to other similar period stats.
Are you aware of the "prime phobia" phenomenon? You would probably be interested in this thread:
http://zodiackillersite.com/viewtopic.php?f=81&t=2841
Yes I remember seeing it in Doranchak’s presentation I am not sure what to make of it or the other quirks he discusses.
Regards
Bart
Today at Lunchtime I After looking at your Graph Smokie i thought i would have a go at making a quick and nasty Frequency analysis on Coincidence counting.
This shows the main frequency spike at 12,24 etc with a massive spike at 108 (9×12)
An interesting exercise that may be of use in future.
Codepad with output.
[url]
http://codepad.org/LYLgscUL
[/url]
#include <stdio.h>
#include <string.h>
unsigned int input[]={20,45,50,34,10,24,26,11,8,46,18,43,31,32,9,45,25,13,14,51,42,29,30,19,12,38,21,31,36,39,36,15,27,33,6,42,42,55,50,1,20,40,33,19,22,37,57,22,28,10,48,19,28,24,27,11,8,47,18,44,45,40,2,23,16,6,33,53,3,5,28,47,12,33,9,56,34,13,48,27,41,35,48,32,42,9,39,40,4,29,26,25,24,44,55,6,30,8,21,23,1,29,23,54,22,7,30,19,2,56,50,41,2,27,36,55,37,57,14,20,29,44,50,35,25,39,36,15,49,18,6,52,28,34,44,31,43,13,45,13,46,19,6,39,26,57,18,2,40,21,43,5,8,57,7,7,17,32,27,47,10,37,20,16,42,36,7,20,21,9,39,7,12,30,15,54,24,19,56,16,38,36,31,42,16,13,54,26,3,6,3,28,29,14,16,55,29,8,29,25,16,39,57,24,21,11,48,19,17,22,44,10,25,43,56,33,11,9,20,49,3,35,50,19,52,48,28,50,35,12,47,18,40,53,24,54,15,47,50,51,10,38,25,32,24,27,14,51,22,37,44,8,34,55,54,42,31,5,44,38,44,48,49,38,4,56,37,18,25,26,54,1,46,49,6,32,43,31,57,32,24,27,20,47,30,48,15,2,5,31,34,44,26,15,33,34,23,57,42,23,11,9,50,9,20,27,32,16,17,18,3,51,44,31,28,44,42,28,7,16,35,4,55,33,12,28,32,6,36,13,7,19,26,23,7,1,25,12,17,14};
//************************************************************************************************************************
void main (void)
{
unsigned int KEoutput[340];
unsigned int index,count,length,offset,segments;
//length = strlen(input); // strlen doesn't work with null data.
length = 340;
for (offset = 0 ; offset <= (length/2) ; offset++)
{
count = 0;
for (index = 0 ; index < (length) ; index++)
{
if ((input[index] == input[(index+offset)%length]))
count++;
}
KEoutput[offset] = count;
}
printf("INDX,KE,Count,segments,count/Segments,Variance2rn");
for (offset = 1 ; offset <= (length/2) ; offset++)
{
count = 0;
segments = 0;
for (index = offset ; index <= (length/2) ; index = index + offset)
{
segments++; //should be lenght/coutn but count them just to be sure..
count = count + KEoutput[index];
}
printf("%04u,%04u,%04u,%04u,%02.2f,%02.2fn",offset,KEoutput[offset],count,segments,(float)count / (float)segments,(float)(5.4-((float)count / (float)segments))*(5.4-((float)count / (float)segments)));
}
}
//************************************************************************************************************************
Ok walk me through this…
you generated 100 random messages.
you homophonicly keyed them with 63 symbol space
but can you please define "diffuse the plaintext inefficiently" i don’t understand this.
If I wanted to make a homophonic key that diffused the plaintext efficiently, then I would map more ciphertext to plaintext like E, and fewer ciphertext to plaintext like B. I have to put the +/- 63 symbols somewhere. But I made keys that had a slightly more uniform allocation of ciphertext. Not quite as many ciphertext for E, and one or two more for B. See the post above, and you can tell the difference. I figured more efficient diffusion would defeat coincidence counting, so I diffused less efficiently to increase whatever spikes I might get.
Ok so just check me here.
You tallied up all the Shift78 across all the messages.
The average spread expected would be 340/63 ~ 5.4 which is what appears you have with a vaguely standard bell curve.
This would mean that the peak of the coincidence counting has moved position between messages.
I tallied 100 values for for each of x=1 to x=170, which gave me 1700 values. Since I made random messages, spikes could occur anywhere on a coincidence counting chart. So I kept all of the 170 x values for each of 100 charts. There were only a small handful of values that were in the same ballpark as the x=78 value of 19 for the 340.
Hmmm… I wonder if we have a frequency mixing going on…
if you mix (two or more) signals together F1 and F2 then depending on the operation you will get Fout = F1+F2, F1*F2 and every mix and combo imaginable.
I wonder if we are seeing Fout and that we have the Letter frequency and symbol frequency beating together.
This is complicated more by the fact that neither is linear.
No idea what you are talking about, but that is o.k. for now.
You guys are doing pretty well compared to some groups and You a pretty wicked with the Excel then
I intended to stick around but like most have limited availability due to work and family life.
In my job i am a hardware engineer but do some programming for hardware bring up and i have only been doing crypto for a short while so i still have plenty learning to go.
There are other groups? No pressure. I have a commute, a full time job, and other commitments. I work on it when I have both the willingness and ability.
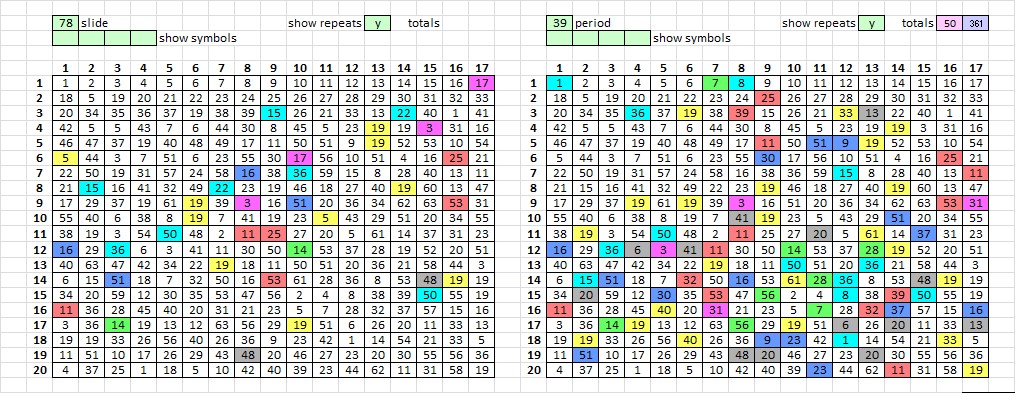
Alright, on the left are the ciphertext involved with your x=78 spike, and on the right I decided to show the ciphertext that are members of period 39 bigram repeats. You can see the pivots there too, because they are period 39 bigram repeat ciphertext.
There are 38 ciphertext highlighted on the left, and EDIT 89 highlighted on the right. Counting by eye, I find that they have 20 in common. I have to get going, but I wonder if you generated a set of 38 random numbers between 1 and 340, and another set of 98 random numbers between 1 and 340, would it be difficult to do that and find that the two sets share at least 20 of the numbers in common.
EDIT: I just did what I described in the paragraph above. Except that with random number generating I didn’t generate any repeat symbols. I tried 100 shuffles, and there was one shuffle where 18 of the numbers in the set of 38 was also in the set of 98.
Hey doranchak, are you out there?
The following discussion is for the Z340.
In the post above: On the left, there are 38 highlighted cells which are symbols involved in Bart’s slide analysis where x=78. On the right, there are 89 highlighted cells which are symbols involved in the period 39 bigram repeats, including the pivot symbols. The two sets of symbols share 20 positions in common.
I randomly selected 38 positions from 340 to create experiment set 1. Then I randomly selected 89 positions from 340 to create experiment set 2. Out of 10,000 trials, I only got two where there were as many as 20 positions shared by both sets.
I did this because I found it interesting because for Bart’s slide analysis, the spike is at x=78, the period 39 bigram repeat "spike", and the pivots. Because 39 * 2 = 78.
What I didn’t do, but just thought of, was to select only 19 random positions for set 1 and then add 78 to their positions. And select 45 random positions for set 2 and then add 39 to their positions. I wonder if that will make a difference.