That’s interesting smokie And Bartw keep at it.
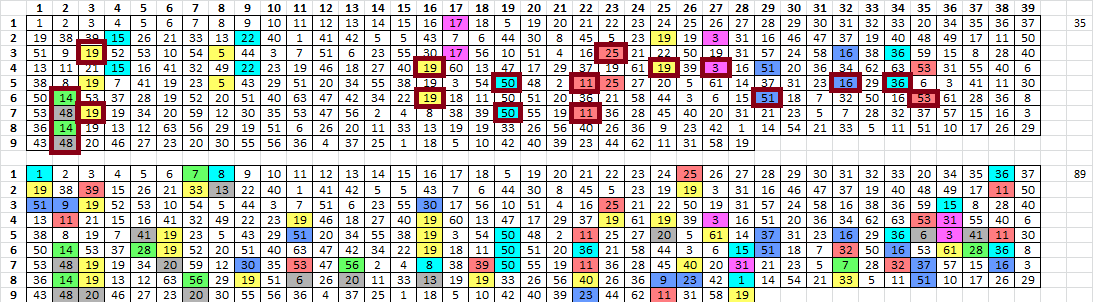
Here, I re-drafted the spreadsheets into 39 columns so that the period 78 unigram repeats and period 39 bigram repeats would line up into columns and make it easy to see. The pivots don’t look like pivots anymore.
My spreadsheet had some issues and I fixed them, but from what I can find at this point, there are 35 positions involved with the period 78 unigram repeats, and 89 positions involved with the period 39 bigram repeats.
Of the 35 positions involved with the period 78 unigram repeats, 19 of them are also involved with the period 39 bigram repeats. All of the above, assuming of course, that he transcribed the message from left to right, top to bottom. 89 / 340 = 26% of the message for positions covered by the bigram repeats. So you would think that roughly 26% of the period 78 unigram repeat positions would fall on period 39 bigram repeat positions. But that is not true. 54% of the period 78 unigram repeat positions fall on period 39 bigram repeat positions.
Why? Does it mean something, or does it mean nothing?
Smokie.
In the Left side of the "coincidence.counting.4.png" it is interesting to see the diagonalish banding of the values.
To me this seems rather unrandom or is that just me??? Also if you look at the hit values.
http://codepad.org/lEOlfjGU#output
dG#+R+pD2c+F4+5|Tt+
There are 5 ‘+’ now in Z340 there are 24 ‘+’ symbols so in 24/340 ~ 7.06% chance of a char being a ‘+’
So in 18 chars we would randomly expect only 1.27 symbols my statistics fall apart about here on conditional probability and Combinations
to work out the chances of getting 5/19 GRRRR!!!!
Anyway to me at the moment it seem to be an anomoly however there is still a chance that this could be just pure luck.
Regards
Bart
Smokie.
In the Left side of the "coincidence.counting.4.png" it is interesting to see the diagonalish banding of the values.
To me this seems rather unrandom or is that just me???
I highlighted the hit positions and the hit positions + 78. In a 17 x 20 grid, they look sort of like they are on diagonal lines. But the diagonals are offset by a couple of spaces and that’s just the pattern of x and x+78. See the post above, where I re-drafted the message into 39 columns so that the x and x+78 positions would line up vertically. To make it easier to see.
There are 5 ‘+’ now in Z340 there are 24 ‘+’ symbols so in 24/340 ~ 7.06% chance of a char being a ‘+’
So in 18 chars we would randomly expect only 1.27 symbols my statistics fall apart about here on conditional probability and Combinations
to work out the chances of getting 5/19 GRRRR!!!! Anyway to me at the moment it seem to be an anomoly however there is still a chance that this could be just pure luck.
Yes, my symbol 19 is the +, and there do seem to be a disproportionate count of them in your period 78 unigram repeat / x=78 slide spike. So is it an anomaly? What is the probability of that happening? How many times would you have to randomly shuffle the message to get a spike like the one that you found, and then discover that 5 of the 24 + symbols land on the spike’s x or x+offset positions? How many semi-cyclic homophonic substitution messages would you have to make, with plaintext randomly taken from some large corpus, and with 63 symbol keys of varying diffusion efficiency, to get a single slide analysis spike like the one that you found. And then discover that 5 of the 24 + symbols land on the spike’s x or x+offset positions"? Oh yeah, and then also discover that only one of the 24 + symbols land on a prime numbered position.
My mind has been racing all night to explain the observations made in the last couple of days. I have to do some quick research, then I will be back with a very general interpretation that can be refined later if necessary.
EDIT: Are you familiar with the period 19 bigram repeat statistics?
Hi Smokie
I am just under the hammer at work for a while but as soon as i can i want to do a IoC column search and see if any anomalies exsist at 78 or factors there of. I think this may aid in clarifying our questions
Regards
Bart
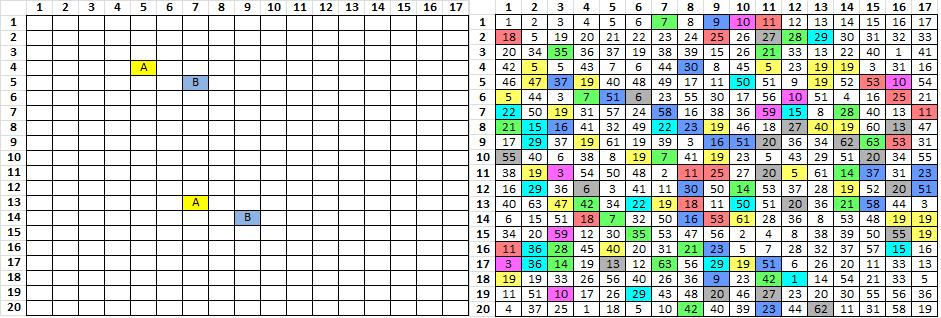
Here is the pairs at various widths
Width = 13 ............. ...d......... ............. ...G....#.... ...........+. R............ ..+....p..... ...d.....D... .....2.c..... ...G....#.... ..+........+. R.F.....4.... ..+....p..... .....5..|D... .....2.c..... .T........... ..+.......... ..F.....4.... .t+.......... .....5..|.... ............. .T......+.... ............. ............. .t........... ............. .. Width = 26 ................d......... ................G....#.... ...........+.R............ ..+....p........d.....D... .....2.c........G....#.... ..+........+.R.F.....4.... ..+....p..........5..|D... .....2.c......T........... ..+............F.....4.... .t+...............5..|.... ..............T......+.... .......................... .t........................ .. Width = 39 ................d...................... ...G....#...............+.R............ ..+....p........d.....D........2.c..... ...G....#......+........+.R.F.....4.... ..+....p..........5..|D........2.c..... .T.............+............F.....4.... .t+...............5..|................. .T......+.............................. .t.......................... Width = 52 ................d.........................G....#.... ...........+.R..............+....p........d.....D... .....2.c........G....#......+........+.R.F.....4.... ..+....p..........5..|D........2.c......T........... ..+............F.....4.....t+...............5..|.... ..............T......+.............................. .t.......................... Width = 65 ................d.........................G....#...............+. R..............+....p........d.....D........2.c........G....#.... ..+........+.R.F.....4......+....p..........5..|D........2.c..... .T.............+............F.....4.....t+...............5..|.... ..............T......+...............................t........... ............... Width = 78 ................d.........................G....#...............+.R............ ..+....p........d.....D........2.c........G....#......+........+.R.F.....4.... ..+....p..........5..|D........2.c......T.............+............F.....4.... .t+...............5..|..................T......+.............................. .t..........................
I hope to have a look at the IoCs at the end of day
Bart, thanks for getting back to me. Don’t worry about not being able to post results all of the time because of work or whatever. I’m not keeping score. This weekend I will be very busy and may not log on for a couple of days. Sometimes I produce more, and sometimes I get tired and produce less. My philosophy is that this is a very difficult message, and I may never solve it. But I do want to make a contribution, and pace myself and keep learning so that I stay interested but don’t burn out.
Thanks in advance for the IoC column search. Take your time.
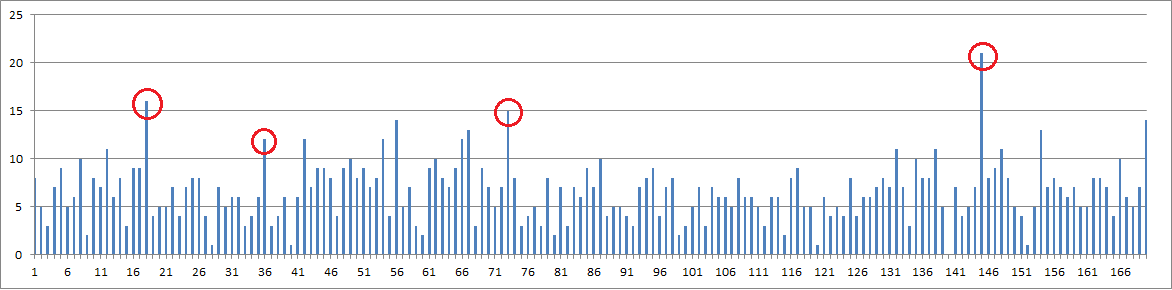
I did the coincidence counting analysis EDIT: ON THE 340 from different directions starting at the corners. The spike moves around on the chart, and here is an example where I moved my x position from the bottom left corner up, working my way from column to column left to right. Until I finished at the upper right corner. With this example, the spike is at 145, but there is also a spike at 73 ( almost half of 145 ). There is a spike at 18 and 36 ( difference of 18 ). There is a spike at 56 and 73 ( difference of 17 ). There is a spike at 170. Note that the difference between 145 and 73 is 72, and 72 / 4 = 18.
So as an aside, I thought of a way to defeat coincidence counting by routing the keyword of a Vigenere cipher in different directions. With a route cipher, you inscribe your message into a geometric shape. Then transcribe the symbols into another geometric shape by some chosen route through the inscription shape. You can go vertical, diagonal, spiral, zig-zag or whatever. With Vigenere, you could basically start with a geometric shape of plaintext, and encode with the keyword with a chosen route.
The more complicated the route, the more difficult it would be to detect Vigenere. Or multiple keys of some sort. Trying different routes could eventually help a cryptanalyst find a coincidence count chart where spikes are at x positions with the same divisors or multipliers.
You could also, intentionally or by mistake, skip a plaintext or add a plaintext null at random or at regular intervals. And that could be detected by adding an extra ciphertext or deleting a ciphertext at each and every position and then making coincidence count charts to find where the skips or nulls make coincidence count spikes appear at the same divisors or multipliers.
One other variation would be to route the keyword encoding so that not all of the plaintext is encoded with the keyword. Only some. Then encoding again with a homophonic substitution key. By doing that, some positions would not be diffused at all by the Vigenere encoding, and possible result in some strange period x bigram repeat statistics of homophonic symbols.
Those are my thoughts for tonight. But this situation where a disproportionate count of x + 78 spike positions are also on period 39 bigram repeat positions is very interesting. I don’t know if one of the cipher steps is Vigenere, but one there may be more than one key, depending on ciphertext position. Some may diffuse less than others, and that may be one way to explain your spike taken together with the period 19 bigram repeat statistics. Just a very rough idea at this point.
Hello Smokie.
Thanks for your previous post i am still thinking about your results and trying to figure out what they mean.
I am not familiar with the period 19 details.
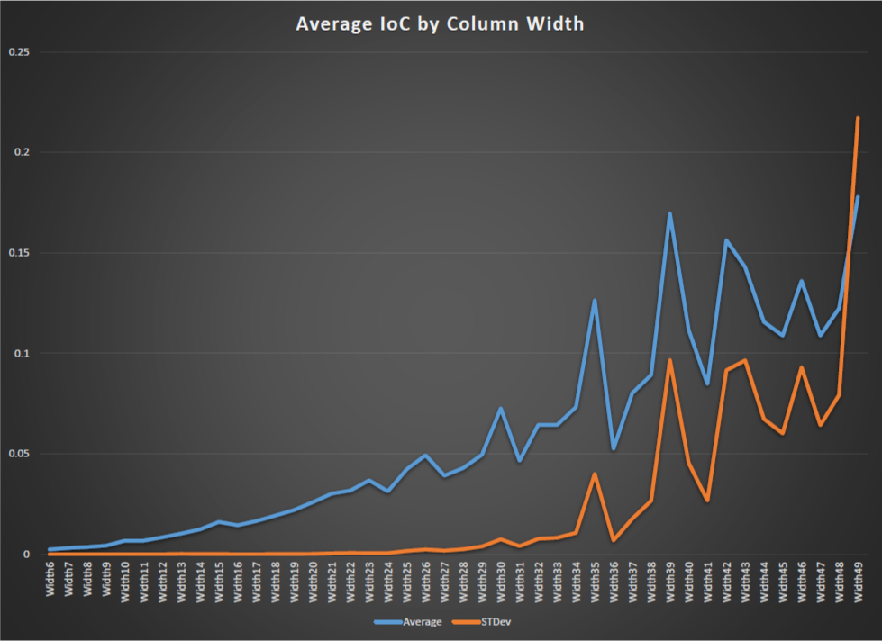
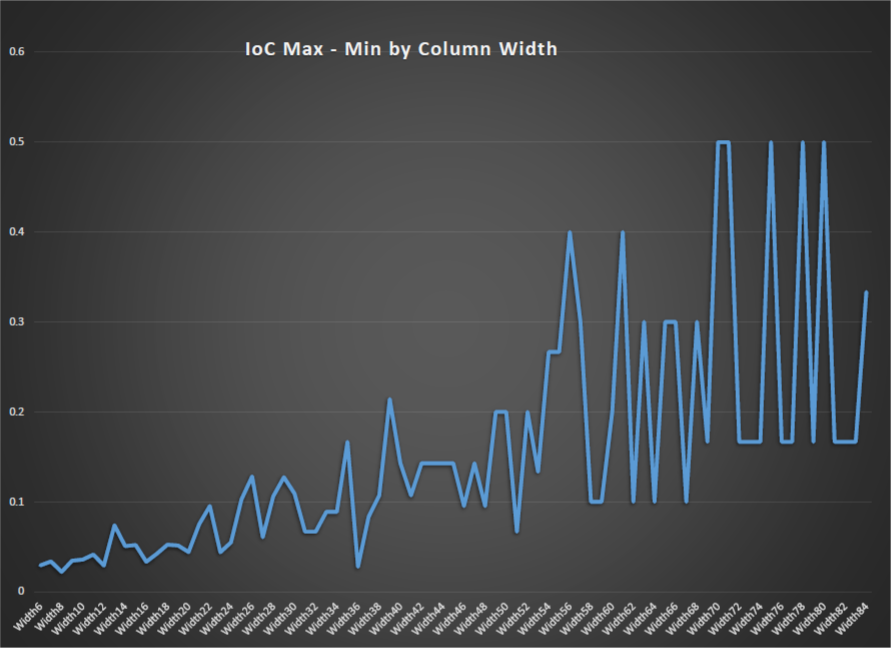
This evening I wrote a program to go through every column arrangement from 6 wide to 84 wide.
it then calculated the IoC of each column and then when it had done each column in the width group it calculated the Average and standard deviation for that width group. This method is also used to determine the keywidth of Vigenere as at the keyword width = column width then all the IoCs (index of coincidence) are approximately equal (or really close compared to other widths).
Anyway so when i plotted the data i somewhat expected to see a trough at 39 and 78 or just 1/F noise (sample noise) instead i ended up with a spike at 39 and 78…
This really has me wondering what the hell is going on.
anyway while I ponder the these results I share them with you all so you can comment or check I haven’t messed up somewhere.
This is a limited range graph showing 6 to 50 so that the spike at 39 could be observed.
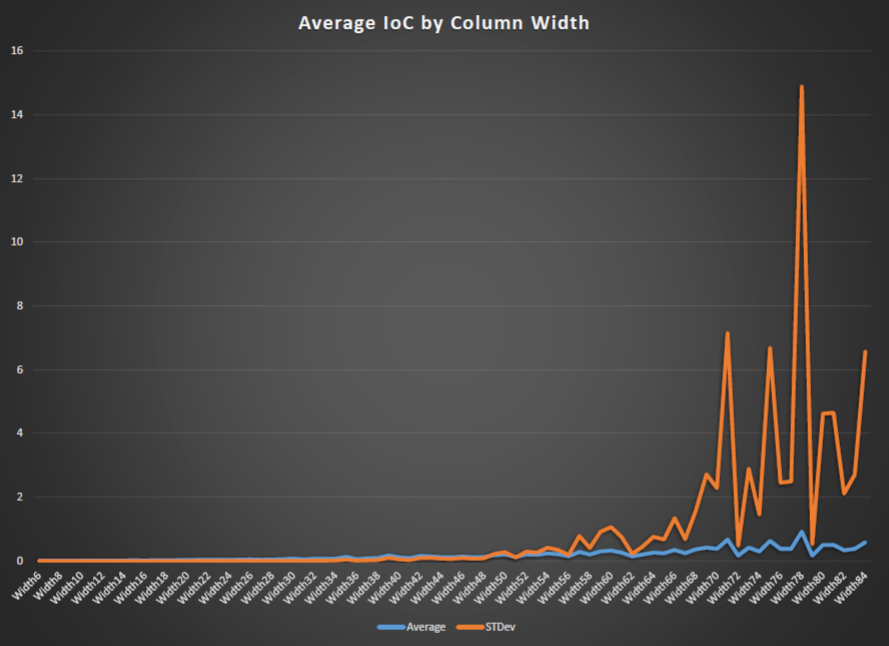
This is the full range graph showing the 1/F noise as well as the spike at 78 which rather large.
the 1/F noise is sampling noise.
This is due to at the width=6 end i have 340/6 =int 56 samples and at the width = 84 end I have only 340/84 = samples.
As i had all the data in Excell i decided to calculate the range of the widths and plot them as well.
Here is the code below at codepad for those who want to have a hack and in the code box below.
The output is intended to be piped to a CSV file and then loaded in excell for graphing and general poking and prodding.
Regards
Bart
http://codepad.org/lwat8wZz#output
#include <stdio.h>
#include <string.h>
unsigned int z340[340]= {
0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10,11,12,13,14,15,16,
17, 4,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,
19,33,34,35,36,18,37,38,14,25,20,32,12,21,39, 0,40,
41, 4, 4,42, 6, 5,43,29, 7,44, 4,22,18,18, 2,30,15,
45,46,36,18,39,47,48,16,10,49,50, 8,18,51,52, 9,53,
4,43, 2, 6,50, 5,22,54,29,16,55, 9,50, 3,15,24,20,
21,49,18,30,56,23,57,15,37,35,58,14, 7,27,39,12,10,
20,14,15,40,31,48,21,22,18,45,17,26,39,18,59,12,46,
16,28,36,18,60,18,38, 2,15,50,19,35,33,61,62,52,30,
54,39, 5,37, 7,18, 6,40,18,22, 4,42,28,50,19,33,54,
37,18, 2,53,49,47, 1,10,24,26,19, 4,60,13,36,30,22,
15,28,35, 5, 2,40,10,29,49,13,52,36,27,18,51,19,50,
39,62,46,41,33,21,18,17,10,49,50,19,35,20,57,43, 2,
5,14,50,17, 6,31,49,15,52,60,27,35, 7,52,47,18,18,
33,19,58,11,29,34,52,46,55, 1, 3, 7,37,38,49,54,18,
10,35,27,44,39,19,30,20,22, 4, 6,27,31,36,56,14,15,
2,35,13,18,12,11,62,55,28,18,50, 5,25,19,10,32,12,
18,18,32,25,55,39,25,35, 8,22,41, 0,13,53,20,32, 4,
10,50, 9,16,25,28,42,47,19,45,26,22,19,29,54,55,35,
3,36,24, 0,17, 4, 9,41,39,38,22,43,61,10,30,57,18};
float proc_ic(unsigned int *workspace, unsigned int len);
//*********************************************************************************************************************
void main (void)
{
unsigned int workspace[408];
unsigned int index,count,length,offset,segments,row,col,width,rowsize;
float pool[100];
float sample,variance,average;
length = 340;
//**** Print CSV header *******
printf("Width,");
for (width = 1; width <= 340/4; width++)
printf("Col%u,",width);
printf("Average,STDevn");
for (width = 6; width < 340/4; width++) //cycle through the widths
{
average = 0; //init average
for (col = 0; col < width; col++) //cycle through the columns
{
for (row = 0; row < (length / width); row++) //cycle through the rows
{
workspace[row]=z340[row * width + col]; //get the z340 char and stuff it into the work array
}
sample = proc_ic(workspace,row); //calc the IoC
pool[col] = sample; //store it for later
average = average + sample; //sum the samples into average
}
average = average / (length/width); //once done with reading the column finish average calc
printf("Width%u,",width); //print width label
variance = 0; //init variance for the stdev calc
for (col = 0; col < (length/4); col++) //go back through the data
{
if(col < width) //if col<width then
{
printf("%f,",pool[col]); //print the sample in csv
variance = variance + ((average - pool[col])*(average - pool[col])); //calc the variance
}
else //else...
{
printf("0,"); // pad the csv column
}
}
printf("%f,",average); // when finished with the column data print the average
variance = variance / (length/width); //finish stdev calc i.e. (variance/Nsamples)
printf("%f,",variance); //print Stdev
printf("n"); //do a line feed
}
}
//************************************************************************************************************************
float proc_ic(unsigned int *workspace, unsigned int len)
{
unsigned int IC_N ;
unsigned long IC_total = 0;
float IC_output = 0;
unsigned int ic_index;
unsigned int freq[63];
//init frequency table
for (ic_index = 0 ; ic_index < 63 ; ic_index++)
freq[ic_index]=0; //Zero workspace.
//calc freq of values
for (ic_index = 0 ; ic_index < len ; ic_index++)
freq[workspace[ic_index]]++;
// Calc IC
IC_total=0;
for (ic_index = 0 ; ic_index < 63 ; ic_index++)
IC_total = IC_total + freq[ic_index]*(freq[ic_index]-1);
IC_N = len;
IC_N = IC_N*(IC_N-1); //for IC calc
IC_output = (float)(1/(float)IC_N)*(float)IC_total;
return(IC_output);
}
I am not familiar with the period 19 details.
Basically there are a lot of period 19 bigram repeats. Practical Cryptography describes them as period 18 bigram repeats. See: http://practicalcryptography.com/crypta … id-cipher/
We started referring to them as period 19 bigram repeats on this site about 8 or 10 months ago and for that time have been trying to figure out what there are so many of them:
Not only is the count of bigram repeats highly improbable, but some of the individual repeats are highly improbable. For example:
A popular explanation was a route transposition, maybe an inscription grid with 19 rows. With a cipher like that, period 1 plaintext repeats would become period 19 repeats after transposition. Period 2 plaintext repeats would become period 38 repeats after transposition. In English plaintext samples, there are typically more period 1 bigram repeats, a few less period 2 bigram repeats, etc. In the 340, we expected to find a spike at period 38, but instead found one at period 39. The pivots are also offset by 39 positions. There has been a massive effort at trying to find a transposition scheme that solves the 340, but with no luck.
When you discovered the slide spike at x=78, that was interesting because 78 / 2 = 39 and 39 / 2 = 19.5.
Your analysis seems to have found related statistics. Figuring that your find is probably not new, I searched this site for "kasiski." But the only substantive discussion is on this thread. Maybe doranchak’s websites discuss your find, I am not sure. We should probably look.
Been casually reading this thread but haven’t had a chance to dive into the full details. Interesting stuff though! I hope to help with the analysis soon.
Anyway, here’s a way to visualize the periodic repeats: http://zodiackillerciphers.com/period-19-bigrams/ Hover your mouse over the buttons to highlight the repeats.
I don’t think I’ve documented the Kasiski/IoC findings yet. I plan to add them once I gain a full understanding of them and their significance. I’ve been trying to summarize everything here: http://zodiackillerciphers.com/wiki/ind … servations
Also, this period calculator is another way to look at the periodic bigram phenomenon: http://zodiackillerciphers.com/period-calculator/
BartW. Go to page 1 of the homophonic substitution thread.. It has lots of tools and interesting breakdowns of the cipher.
I’m starting at the basics, so I did a shuffle test of the Kasiski exam spike at shift of 78. In my tests, the number of repeats (coincidences) peaks at 18 at the shift of 78. I think you guys are getting 19. Perhaps my counting is off? (UPDATED: Maybe it’s because I’m counting the number of gaps involved in the repeats, instead of the total number of repeating ngrams)
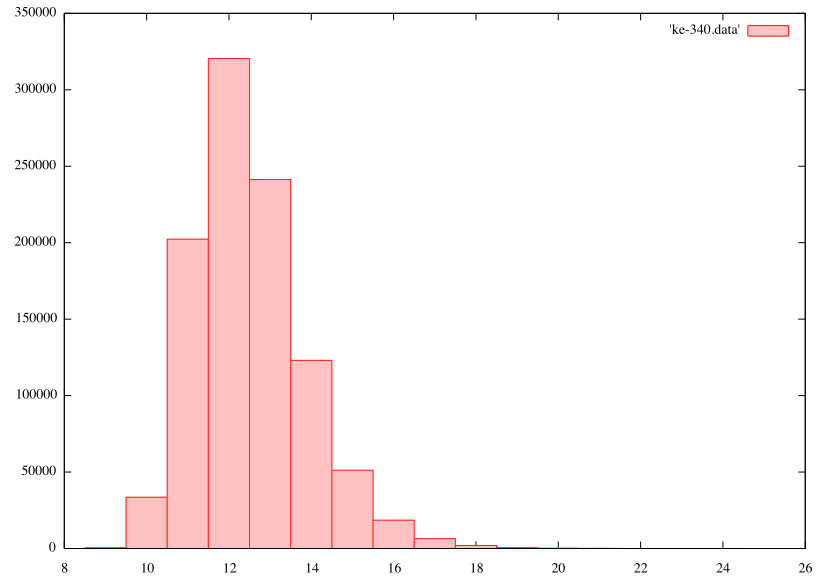
Anyway, I want to know if the spike is significant, so I compared it to 1,000,000 random shuffles. In each shuffle, every shift value is tested, and the one producing the largest number of repeated symbols (coincidences) is retained.
First number is maximum repeats observed. Second number is number of shuffles having exactly that number of repeats.
9 486
10 33527
11 202275
12 320453
13 241319
14 123010
15 51176
16 18514
17 6458
18 1971
19 570
20 172
21 55
22 10
23 2
24 2
Here’s a plot of the above distribution:
Min repeats: 9.0
Max repeats: 24.0
Mean: 12.494258999999992
Std Dev: 1.3652702680680797
Z340 has max repeats of 18 at a shift of 78. This is about 4 standard deviations from the mean.
Of the 1,000,000 shuffles, only 2,782 of them (0.28%) had equal or better number of repeats.
So, it seems the phenomenon is rather significant compared to random ciphertext. And 78 is curiously related to the period 39 pivots (78 = 39 * 2). I will try to digest the rest of this thread to catch up to you guys.
Curiously, Z408 has a spike at shift 49 and the number of repeats is the same: 18.
Running the same shuffle test, 22,038 of the shuffles (2.2%) had a spike as good or better than the one observed in Z408.
10 39
11 8445
12 104053
13 271619
14 285662
15 181963
16 88991
17 37190
18 14369
19 5119
20 1743
21 564
22 163
23 58
24 17
25 3
26 2
Min: 10.0
Max: 26.0
Mean: 14.065828999999994
Std Dev: 1.448623360733466
Z408’s spike of 18 is 2.7 standard deviations from the mean.
This suggests that relative to Z340’s spike, the spike in Z408 is less significant.
By doing the same on Z340 a Spike was noted at a shift of 78 and a slight above average at 39 (78/2) with no noticeable harmonic at 156 (2*78).
What do you think about the y-value of the spike?
I don’t know. It is over 3 * the mean from memory which is some what significant and has a reasonable SNR(signal to noise) but this is also the first time i have encountered a Homophonic cipher so I do not have a full appreciation for the interaction of the higher symbol space. Also the lack of sub/harmonics lowers my confidence in its validity.
I implemented your code to reproduce your data. Its mean is 6.60, and standard deviation is 2.82. So, the peak of 19 is 4.40 standard deviations from the mean.
It might be a good idea to look at the KE data for these test ciphers, to see how often such peaks occur for non-random cipher texts with real messages: https://docs.google.com/spreadsheets/d/ … sp=sharing (I see that smokie already did something like that in this thread with his own generated ciphers).