I implemented a normalization step for BartW’s columnar IoC test.
Let’s look at width 78. We write Z340 into 78 columns, which results in 5 rows that look like this:
HER>pl^VPk|1LTG2dNp+B(#O%DWY.<*Kf)By:cM+UZGW()L#zHJSpp7^l8*V3pO++RK2_9M+ztjd|5 FP+&4k/p8R^FlO-*dCkF>2D(#5+Kq%;2UcXGV.zL|(G2Jfj#O+_NYz+@L9d<M+b+ZR2FBcyA64K-zl UV+^J+Op7<FBy-U+R/5tE|DYBpbTMKO2<clRJ|*5T4M.+&BFz69Sy#+N|5FBc(;8RlGFN^f524b.cV 4t++yBX1*:49CE>VUZ5-+|c.3zBK(Op^.fMqG2RcT+L16C<+FlWB|)L++)WCzWcPOSHT/()p|FkdW< 7tB_YOB*-Cc>MDHNpkSzZO8A|K;+
Now let’s compute IoC, one column at a time:
column#, ioc, string 0 0.0 HFU47 1 0.1 EPVtt 2 0.3 R+++B 3 0.0 >&^+_ 4 0.0 p4JyY 5 0.0 lk+BO 6 0.0 ^/OXB 7 0.1 Vpp1* 8 0.0 P87*- 9 0.0 kR<:C 10 0.0 |^F4c 11 0.0 1FB9> 12 0.0 LlyCM 13 0.0 TO-ED 14 0.0 G-U>H 15 0.0 2*+VN 16 0.1 ddRUp 17 0.0 NC/Zk 18 0.1 pk55S 19 0.0 +Ft-z 20 0.0 B>E+Z 21 0.1 (2||O 22 0.1 #DDc8 23 0.0 O(Y.A 24 0.0 %#B3| 25 0.0 D5pzK 26 0.0 W+bB; 27 0.1 YKTK+ 28 0.0 .qM( 29 0.0 <%KO 30 0.0 *;Op 31 0.16666666666666666 K22^ 32 0.0 fU<. 33 0.16666666666666666 )ccf 34 0.0 BXlM 35 0.0 yGRq 36 0.0 :VJG 37 0.0 c.|2 38 0.0 Mz*R 39 0.0 +L5c 40 0.16666666666666666 U|TT 41 0.0 Z(4+ 42 0.16666666666666666 GGML 43 0.0 W2.1 44 0.0 (J+6 45 0.0 )f&C 46 0.0 LjB< 47 0.16666666666666666 ##F+ 48 0.16666666666666666 zOzF 49 0.0 H+6l 50 0.0 J_9W 51 0.16666666666666666 SNSB 52 0.0 pYy| 53 0.0 pz#) 54 0.16666666666666666 7++L 55 0.0 ^@N+ 56 0.0 lL|+ 57 0.0 895) 58 0.0 *dFW 59 0.0 V<BC 60 0.0 3Mcz 61 0.0 p+(W 62 0.0 Ob;c 63 0.16666666666666666 ++8P 64 0.0 +ZRO 65 0.16666666666666666 RRlS 66 0.0 K2GH 67 0.16666666666666666 2FFT 68 0.0 _BN/ 69 0.0 9c^( 70 0.0 Myf) 71 0.0 +A5p 72 0.0 z62| 73 0.16666666666666666 t44F 74 0.0 jKbk 75 0.16666666666666666 d-.d 76 0.0 |zcW 77 0.0 5lV<
Now we can compute the mean of all those IoC’s: 0.04060
And the standard deviation: 0.07140
How significant is the mean of 0.04060? Maybe we can compare it to what we expect the mean to be if the cipher was completely random.
So, make a completely random shuffle of Z340 and write it to width 78 again. Compute the mean of all the column IoCs. Repeat this 10,000 times, and then compute the mean of the means. The result is an estimate of the expected mean of column IoC at width 78.
One run of 10,000 shuffles results in a list of 10,000 means. The mean of these means is 0.01945, which we can interpret as “0.01945 is the expected mean column IoC for random cipher texts at width 78.” The standard deviation for all 10,000 means is 0.005808. For Z340, the actual mean IoC was 0.04060. How far is that from the expected mean? Answer: 0.04060 – 0.01945 = 0.02115. How many standard deviations is that? Answer: 0.02115/0.005808 = 3.642. In other words, the spike IoC of 0.04060 we observe at width 78 is 3.642 sigma away from what we expect to see for random cipher text.
So for Z340, let’s plot sigma for all widths (by comparing Z340 to 10,000 shuffles for each width) to see where the significant spikes might be:
Widths 2-60:

Widths 60-120:

Widths 120-170:

All widths:

Width 78 tops the list at 3.6 sigma. One thing that stands out: Multiples of 5 seem to resonate. Here’s the list of all widths that had sigma of at least 1, and multiples of 5 are boldfaced:
Width 78: 3.6446412092890053
Width 75: 3.4276047081236722
Width 150: 3.216662144067663
Width 162: 3.063912336942132
Width 109: 2.94557512876493
Width 35: 2.896680004531257
Width 42: 2.75783419836278
Width 6: 2.715827681367133
Width 39: 2.644332306853863
Width 105: 2.583043193599122
Width 30: 2.377438418510436
Width 71: 2.2298278569531127
Width 10: 2.090293451426147
Width 129: 1.843069286141543
Width 113: 1.7687972858022973
Width 137: 1.7685214504983309
Width 26: 1.7112983020046126
Width 15: 1.70923804374948
Width 69: 1.6931412422246994
Width 106: 1.6625280045792235
Width 133: 1.6522103952244984
Width 149: 1.6271547675505167
Width 5: 1.621432570307188
Width 43: 1.605992671445837
Width 25: 1.5834808392724258
Width 136: 1.5525663337297686
Width 110: 1.4945155066034967
Width 7: 1.4848156888889792
Width 81: 1.4690357754972152
Width 163: 1.467518276985967
Width 84: 1.4590843583463469
Width 70: 1.4334487029991467
Width 3: 1.419302215099044
Width 80: 1.4175999400022854
Width 68: 1.3823847819021202
Width 142: 1.3784916135027645
Width 120: 1.3569390464816289
Width 143: 1.3350714623639035
Width 21: 1.315531227174728
Width 40: 1.3066508107526904
Width 23: 1.294585344399885
Width 128: 1.2936292091891937
Width 100: 1.260397907803027
Width 60: 1.2535694215548872
Width 115: 1.2465852947216836
Width 50: 1.1980601692619552
Width 66: 1.1688398476319215
Width 93: 1.117759670198255
Width 2: 1.1080112206787167
Width 119: 1.0315484243594117
Width 20: 1.0299769159534773
Width 147: 1.0120433894639103
There are 52 entries there, and 19 of them (37%) are multiples of 5. Wouldn’t the expected number of multiples of 5 be around 52/5 = 10 (20%)?
I will run this same procedure for Z408 for comparison when I get a chance.
I tried to reproduce your data with my own program. It is close but there are some differences.
Hi David thanks for taking the time to scrutinize my findings.
Here are our sample strings side by side
column 1: H^Lp%*:Gz73KzF/lk#;VGO+M26UOy5BOJMz+cG24XC53pGLFLzH|7BMS| Col = 0 H^Lp%*:Gz73KzF/lk#;VGO+M26UOy5BOJMz+cG24XC53pGLFLzH|7BMS column 2: EVT+DKcWH^p2tPpOF52.2+@+F4Vp-tp2|.6N(F4t1E-z^21l+WTFt*DzK Col = 1 EVT+DKcWH^p2tPpOF52.2+@+F4Vp-tp2|.6N(F4t1E-z^21l+WTFt*Dz column 3: RPGBWfM(JlO_j+8->+UzJ_LbBK+7UEb<*+9|;Nb+*>+B.R6W+c/kB-HZ; Col = 2 RPGBWfM(JlO_j+8->+UzJ_LbBK+7UEb<*+9|;Nb+*>+B.R6W+c/kB-HZ column 4: >k2(Y)+)S8+9d&R*2KcLfN9+c-^<+|Tc5&S58^.+:V|KfcCB)P(d_CNO+ Col = 3 >k2(Y)+)S8+9d&R*2KcLfN9+c-^<+|Tc5&S58^.+:V|KfcCB)P(d_CNO column 5: p|d#.BULp*+M|4^dDqX|jYdZyzJFRDMlTByFRfcy4Uc(MT<|WO)WYcp8 Col = 4 p|d#.BULp*+M|4^dDqX|jYdZyzJFRDMlTByFRfcy4Uc(MT<|WO)WYcp8 column 6: l1NO<yZ#pVR+5kFC(%G(#z<RAl+B/YKR4F#Bl5VB9Z.Oq++)CSp<O>kA Col = 5 l1NO<yZ#pVR+5kFC(%G(#z<RAl+B/YKR4F#Bl5VB9Z.Oq++)CSp<O>kA
First of the the bat we are using slightly different sample strings and methods.
I use length/width cast to an Interger so I effectively loose the remainder. I did this so that all my samples were the same length.
You don’t and so have the entire message with dissimilar length… Your method would be more correct we do however have the same last two columns.
Index of coincidence side by side column 1: 0.019423558897243107 Col0IoC = 0.019480518997 column 2: 0.02882205513784461 Col1IoC = 0.029220778495 column 3: 0.02443609022556391 Col2IoC = 0.024675324559 column 4: 0.023809523809523808 Col3IoC = 0.021428572014 column 5: 0.01948051948051948 Col4IoC = 0.019480518997 column 6: 0.02142857142857143 Col5IoC = 0.021428572014
So as expected out columns 1 to 4 are slightly out but out 5 and 6 are pretty close.
I am using a 32bit C float is your float 64bit? if so this may account for the remaining rounding variation on Column 5&6
So to calculate Standard deviation i first calculate the average.
Average = sum(samples)/n Samples
Then i calculated the variance for each sample
variance = (sample-average)*(sample-average)
The Standard deviation i calculate as below.
Sum (variance)/N Samples.
hopefully this method relates to yours?
Regards
Bart
Hi Smokie,
I am finding an interesting trend with the multiobjective evolution messages. I have checked more than a dozen at the bottom of the list when the website spreadsheet is sorted by column B.
if your coincidence counting algorithm does not wrap around you will loose Y as you progress..
the reason for this is once you are at position 200 you now are doing a coincidence count on the maximum potential of 140.
at a gerneal average chance of 2% for a pair or so this will inevitably show as a downward trending slope.
however if do wrap around you will get a mirror image at location 170 with 1 and 340 begin the same 2 = 339 etc etc.
Does this make sense?
Regards
Bart
Hi David,
This is Very interesting. unfortunately i really need to work on my stats maths.
Isn’t a sigma a Stdev unit? if so 3 sigma must be in the top 0.1% i.e. some what significant!
I will mull this over in the mean while but it would be interesting to see what Z408 coughs up when you get the time.
Regards
Bart
I implemented a normalization step for BartW’s columnar IoC test.
How significant is the mean of 0.04060? Maybe we can compare it to what we expect the mean to be if the cipher was completely random.
So, make a completely random shuffle of Z340 and write it to width 78 again. Compute the mean of all the column IoCs. Repeat this 10,000 times, and then compute the mean of the means. The result is an estimate of the expected mean of column IoC at width 78.
One run of 10,000 shuffles results in a list of 10,000 means. The mean of these means is 0.01945, which we can interpret as “0.01945 is the expected mean column IoC for random cipher texts at width 78.” The standard deviation for all 10,000 means is 0.005808. For Z340, the actual mean IoC was 0.04060. How far is that from the expected mean? Answer: 0.04060 – 0.01945 = 0.02115. How many standard deviations is that? Answer: 0.02115/0.005808 = 3.642. In other words, the spike IoC of 0.04060 we observe at width 78 is 3.642 sigma away from what we expect to see for random cipher text.
I will run this same procedure for Z408 for comparison when I get a chance.
So as expected out columns 1 to 4 are slightly out but out 5 and 6 are pretty close.
I am using a 32bit C float is your float 64bit? if so this may account for the remaining rounding variation on Column 5&6
Yes, I am using java’s "double" type which is 64 bit.
So to calculate Standard deviation i first calculate the average.
Average = sum(samples)/n Samples
Then i calculated the variance for each sample
variance = (sample-average)*(sample-average)
The Standard deviation i calculate as below.
Sum (variance)/N Samples.
hopefully this method relates to yours?
Yes, I believe our average and std dev calculations are done the same way.
Hi David,
This is Very interesting. unfortunately i really need to work on my stats maths.
Isn’t a sigma a Stdev unit? if so 3 sigma must be in the top 0.1% i.e. some what significant!
Yes – one sigma equals one standard deviation. Three sigma indeed seems significant. However, the 408 has a 4 sigma spike at width 61. I’ll post the results and plots shortly.
Here are the sigma plots for Z408:
Widths 2-68:

Widths 68-136:
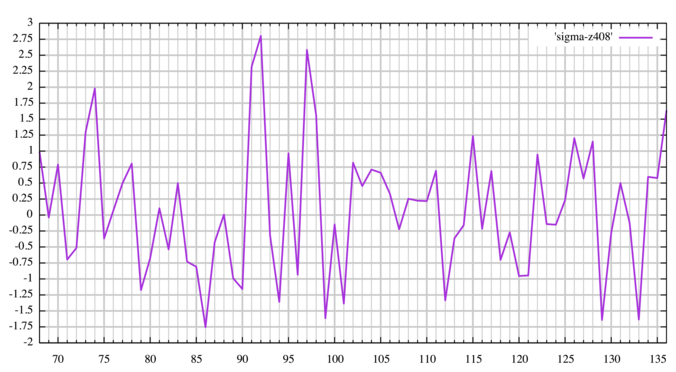
Widths 136-204:

All widths:

Here are the best widths, sorted by sigma, having a sigma >= 1:
Width 61: 4.1719903996941525
Width 163: 2.8539411953060614
Width 49: 2.82388632841443
Width 92: 2.8018832933145807
Width 97: 2.583501050592803
Width 91: 2.3191598150402233
Width 23: 2.2494233201543876
Width 149: 2.187766089858773
Width 74: 1.9796732199779217
Width 16: 1.956118255743881
Width 46: 1.917056845261938
Width 21: 1.8743310819154648
Width 169: 1.7307921583439208
Width 136: 1.636635590917913
Width 189: 1.620345606545015
Width 173: 1.6142334565270917
Width 39: 1.6128751217410209
Width 63: 1.582657116452049
Width 98: 1.562222317434836
Width 145: 1.5419357530983835
Width 32: 1.3927185043513899
Width 64: 1.3837177480902465
Width 141: 1.3587376991680131
Width 194: 1.319813448216958
Width 73: 1.2988530318277587
Width 53: 1.2908259595538178
Width 115: 1.2358763554723982
Width 126: 1.2015949300810287
Width 128: 1.1487966927221636
Width 166: 1.1061801813896266
Width 35: 1.1015044860824064
Width 157: 1.086428789582543
Width 176: 1.0853614493704415
Width 187: 1.0748033499533007
Width 37: 1.0411173341626458
In Z408, only 35 out of 204 widths tested had a sigma >= 1. That’s 17% of the widths.
In Z340, 54 out of 170 widths tested had a sigma >= 1. That’s 32% of the widths.
I don’t know what to make of the peak at 61. Could it just be a reflection of cycling? Perhaps a better test would be to compute sigma for a large collection of actual homophonic substitution ciphers rather than completely randomized ciphertext. But then there would be complicating factors such as how to fairly represent varying levels of regularity in the cycling of homophones.
Here is the breakdown of common divisors found within the widths that produced sigmas greater than or equal to one.
The first number is the divisor, then the number in parentheses is how many widths share that divisor.
Z340: 2 (25), 3 (21), 5 (19), 10 (12), 7 (10), 6 (10), 4 (10), 15 (7), 20 (6), 8 (5), 25 (5), 21 (5), 30 (4), 13 (4), 50 (3), 40 (3), 35 (3), 23 (3), 17 (3), 14 (3), 12 (3), 11 (3), 9 (2), 81 (2), 75 (2), 71 (2), 68 (2), 60 (2), 43 (2), 42 (2), 39 (2), 34 (2), 27 (2), 26 (2), 22 (2), 16 (2)
Z408: 2 (13), 7 (8), 4 (7), 8 (6), 3 (6), 16 (5), 23 (4), 21 (4), 9 (3), 63 (3), 5 (3), 32 (3), 13 (3), 97 (2), 64 (2), 49 (2), 46 (2), 37 (2), 17 (2), 14 (2), 11 (2)
Hi Smokie,
I am finding an interesting trend with the multiobjective evolution messages. I have checked more than a dozen at the bottom of the list when the website spreadsheet is sorted by column B.
if your coincidence counting algorithm does not wrap around you will loose Y as you progress..
the reason for this is once you are at position 200 you now are doing a coincidence count on the maximum potential of 140.
at a gerneal average chance of 2% for a pair or so this will inevitably show as a downward trending slope.
however if do wrap around you will get a mirror image at location 170 with 1 and 340 begin the same 2 = 339 etc etc.Does this make sense?
Regards
Bart
Yes, it does make sense. My first spreadsheet was wraparound, but I thought that the mirror image was duplicitous so I dropped it. However, I think that wraparound should probably be step 2.
For example, you could have a suspected keyword length of 6 letters, and that is not a divisor of 340 ( 6 * 56 = 336 and 6 * 7 = 342 ). So when you get to the end of the message, your coincidence counting will be incorrect. It seems to me that you should add nulls at the end of the message. You could add one null to start with, count your repeats with wraparound. Then add two nulls and count your repeats with wraparound. Then with three nulls, four nulls, etc. Comparing results with different counts of nulls should help to confirm your suspected key lengths.
Z408 has a significant Kasiski peak at width 61. Here’s a visualization of the doubles that show up when writing the cipher at that width:
http://zodiackillerciphers.com/images/z … oubles.png
Programs and data sets can be made available on request.
Regards
Bart
Can you post the Vigenere cipher you used for you columnar IoC test? I want to run it through my process that compares it with shuffles, to see how the sigma plots compare to those of Z340 and Z408.
Doranchak, thank you for making the spreadsheet and keeping track of everyone’s messages. That is a lot of work and I appreciate it. It came in handy today.
Cool – I’m very happy that it has found some use.
So looking at your results, it appears that it’s not so unusual for homophonic substitution ciphers to produce spikes of 18+ when using Kasiski examination to do coincidence counting. Is that a fair statement?
Doranchak, thank you for making the spreadsheet and keeping track of everyone’s messages. That is a lot of work and I appreciate it. It came in handy today.
Cool – I’m very happy that it has found some use.
So looking at your results, it appears that it’s not so unusual for homophonic substitution ciphers to produce spikes of 18+ when using Kasiski examination to do coincidence counting. Is that a fair statement?
Yeah, I think that is a fair statement.
I don’t know if coincidence counting detected a Vigenere step in the 340 cipher, but it may have detected some other cipher step that we don’t know about. Vigenere diffuses the plaintext so much that if Zodiac did that, I cannot see how we could have so many period 19 repeats.
Two of the possible options are Vigenere before transposition, and transposition before Vigenere. If you did Vigenere before transposition, then the plaintext would be diffused so much that finding so many period 19 bigram repeats would be pretty improbable. On the other hand, if you transposed a message and then used Vigenere, you could have a lot of period 19 repeats – if the key was 19 letters long.
If Zodiac transcribed the plaintext right to left, top row to bottom row, from an inscription rectangle that had 15 columns or rows, then maybe using a Vigenere key of length 3, 5, or 15 could result in a lot of period 15 bigram repeats. Because multiple of the key word length just happens to align with the transposition period. I would have to explore that idea further, but the only divisor of 78 mentioned is 3.
You found a significant IoC spike with the 408, but the 408 is not a Vigenere message. But I think that the count of shared positions with the period 26 and 39 bigram repeats, both divisors of 78 and taking into account the period of the pivot repeats, 39, warrants not dismissing the x = 78 spike. Looking at other transcription or Vigenere directions and routes may reveal other surprises. Is there a path that you could take through the message that would make spike at equal intervals? Even if there was, how could that explain the period 19 repeats?
I also like the idea of trying to find a cipher that could explain all.
Can you post the Vigenere cipher you used for you columnar IoC test? I want to run it through my process that compares it with shuffles, to see how the sigma plots compare to those of Z340 and Z408.
Here you go hopefully it is till relevant.
ASCII
KEAGRDZFGDCGFNTQO GHQTZQPGORXODKKFB YCXGEDHFPBBBMZNOT PNIBCTFRPGTPNIHOF NMUZPXXGUWWQNCBTY WTZDEZZNHMZGKCMPS CUHZRFWQFRQPIFUTE PWICPGORKEDPRRXTS RZSEEFKBHBZZRYKJC CZWZYEDOZLIMCKECU RYCGHFKECAFZGHMCI FNMGIRXGTUIMMZZMC BBZFCURYCGHFIFDQK EADFAUEPMTCYCZSIZ PTGIGHLMTFNKOFSHP WZYCAFZYHMZKPADGS MIAOYZTAHJRTIGZYA FGEAGRDZRMQUJYZXZ UNEMGIRWXQUECQRKQ PKSJZSFKEAIBBIIYB ZFEGTDNPEERZAXTZR PCXCJQXZORTRKRKMZ KOZYYOQUCHZSTZRMN CWHNPYKIFWKCSBTLZ RQPKJTGUZYSFTZLZL CLTHMTRAIXFYZNFJZ MJMDAKWTKCCRBDNZR EIZLTKORCYEWSQIBH AKEFJZQPFSTLMNGIM UZZGIAOZZPHTGGIEU PGSIMZKIEMTZCMZSZ KIAPJYCWGUDEOKGFT KGEJTQOJKPRIYZSXK XFIEMSFRQQIDTPSXT HMTRAIXFYNHQPFSII IZREDULQIASTLMNGI RWTHCZRQKENJMQUUE EQGCGTHKUBKULZHMW ZLTUPXYRZCXUIZIKM PEOXXEOQUCQHCQNHU
Number sequence 0 = A etc
10,4,0,6,17,3,25,5,6,3,2,6,5,13,19,16,14, 6,7,16,19,25,16,15,6,14,17,23,14,3,10,10,5,1, 24,2,23,6,4,3,7,5,15,1,1,1,12,25,13,14,19, 15,13,8,1,2,19,5,17,15,6,19,15,13,8,7,14,5, 13,12,20,25,15,23,23,6,20,22,22,16,13,2,1,19,24, 22,19,25,3,4,25,25,13,7,12,25,6,10,2,12,15,18, 2,20,7,25,17,5,22,16,5,17,16,15,8,5,20,19,4, 15,22,8,2,15,6,14,17,10,4,3,15,17,17,23,19,18, 17,25,18,4,4,5,10,1,7,1,25,25,17,24,10,9,2, 2,25,22,25,24,4,3,14,25,11,8,12,2,10,4,2,20, 17,24,2,6,7,5,10,4,2,0,5,25,6,7,12,2,8, 5,13,12,6,8,17,23,6,19,20,8,12,12,25,25,12,2, 1,1,25,5,2,20,17,24,2,6,7,5,8,5,3,16,10, 4,0,3,5,0,20,4,15,12,19,2,24,2,25,18,8,25, 15,19,6,8,6,7,11,12,19,5,13,10,14,5,18,7,15, 22,25,24,2,0,5,25,24,7,12,25,10,15,0,3,6,18, 12,8,0,14,24,25,19,0,7,9,17,19,8,6,25,24,0, 5,6,4,0,6,17,3,25,17,12,16,20,9,24,25,23,25, 20,13,4,12,6,8,17,22,23,16,20,4,2,16,17,10,16, 15,10,18,9,25,18,5,10,4,0,8,1,1,8,8,24,1, 25,5,4,6,19,3,13,15,4,4,17,25,0,23,19,25,17, 15,2,23,2,9,16,23,25,14,17,19,17,10,17,10,12,25, 10,14,25,24,24,14,16,20,2,7,25,18,19,25,17,12,13, 2,22,7,13,15,24,10,8,5,22,10,2,18,1,19,11,25, 17,16,15,10,9,19,6,20,25,24,18,5,19,25,11,25,11, 2,11,19,7,12,19,17,0,8,23,5,24,25,13,5,9,25, 12,9,12,3,0,10,22,19,10,2,2,17,1,3,13,25,17, 4,8,25,11,19,10,14,17,2,24,4,22,18,16,8,1,7, 0,10,4,5,9,25,16,15,5,18,19,11,12,13,6,8,12, 20,25,25,6,8,0,14,25,25,15,7,19,6,6,8,4,20, 15,6,18,8,12,25,10,8,4,12,19,25,2,12,25,18,25, 10,8,0,15,9,24,2,22,6,20,3,4,14,10,6,5,19, 10,6,4,9,19,16,14,9,10,15,17,8,24,25,18,23,10, 23,5,8,4,12,18,5,17,16,16,8,3,19,15,18,23,19, 7,12,19,17,0,8,23,5,24,13,7,16,15,5,18,8,8, 8,25,17,4,3,20,11,16,8,0,18,19,11,12,13,6,8, 17,22,19,7,2,25,17,16,10,4,13,9,12,16,20,20,4, 4,16,6,2,6,19,7,10,20,1,10,20,11,25,7,12,22, 25,11,19,20,15,23,24,17,25,2,23,20,8,25,8,10,12, 15,4,14,23,23,4,14,16,20,2,16,7,2,16,13,7,20
Regards
Bart
I don’t know if coincidence counting detected a Vigenere step in the 340 cipher, but it may have detected some other cipher step that we don’t know about.
Vigenere diffuses the plaintext so much that if Zodiac did that, I cannot see how we could have so many period 19 repeats.
for this would happen the plain text and both the Vigenere key and the Homophonic Key would need to for both instances to strike a count.
Two of the possible options are Vigenere before transposition, and transposition before Vigenere. If you did Vigenere before transposition, then the plaintext would be diffused so much that finding so many period 19 bigram repeats would be pretty improbable. On the other hand, if you transposed a message and then used Vigenere, you could have a lot of period 19 repeats – if the key was 19 letters long.
I Agree with your statement. is there any evidence that apart from the homophonic layer that there is another cipher layer? (apart from homophonic not solving)
You found a significant IoC spike with the 408, but the 408 is not a Vigenere message. But I think that the count of shared positions with the period 26 and 39 bigram repeats, both divisors of 78 and taking into account the period of the pivot repeats, 39, warrants not dismissing the x = 78 spike.
it would appear that the Coincidence count is merely an interpretation of the 26/39 bigram anomaly.
I also like the idea of trying to find a cipher that could explain all.
it would be another metric to test against however i suspect you find the bigrams you will find the spike.
Regards
Bart
Here you go hopefully it is still relevant.
Thanks. I ran the shuffle-based columnar IoC normalization on it and it did a pretty good job of identifying the resonances:
Widths 2-85:

Widths 85-170:

Widths 170-255:

Widths 255-340:

All widths:

Top 20 widths by sigma:
Width 10: 21.294990457999447
Width 5: 15.006581248489393
Width 20: 14.108218946326215
Width 30: 11.3013302155331
Width 50: 9.55344015553748
Width 40: 9.403765518378105
Width 15: 7.883816073703713
Width 25: 7.081732776680419
Width 60: 7.022312596236516
Width 150: 6.426360319898618
Width 110: 6.313889323138694
Width 80: 6.161098903072606
Width 100: 5.700515869565677
Width 70: 5.649226418827615
Width 160: 5.429565053290519
Width 300: 4.88896718690515
Width 230: 4.797547584695648
Width 2: 4.5073420267446656
Width 130: 4.471588186554279
Width 170: 4.4598387851683094
I especially like that the sigma of 21 for width 10 leaves little doubt about the key length!
