Here you go hopefully it is still relevant.
Thanks. I ran the shuffle-based columnar IoC normalization on it and it did a pretty good job of identifying the resonances I especially like that the sigma of 21 for width 10 leaves little doubt about the key length!
Wow! that works really well. definitely going to need to try that again in the future.
Hmm now the question is if we put a homophonic layer over the top how does it affected the length harmonic.
I was surprised to see the sub harmonic 5 but this makes perfect sense when you think about it as 50% of the key would correlate.
Wow! that works really well. definitely going to need to try that again in the future.
Hmm now the question is if we put a homophonic layer over the top how does it affected the length harmonic.
I was surprised to see the sub harmonic 5 but this makes perfect sense when you think about it as 50% of the key would correlate.
Here is the same process applied to ALisowsky’s vigenere cipher (source). Here’s the result before he applied homophonic encipherment:

The peak appears to be at the true key length (5), with a sigma of 14.6. Here’s the result after he applied homophonic encipherment:
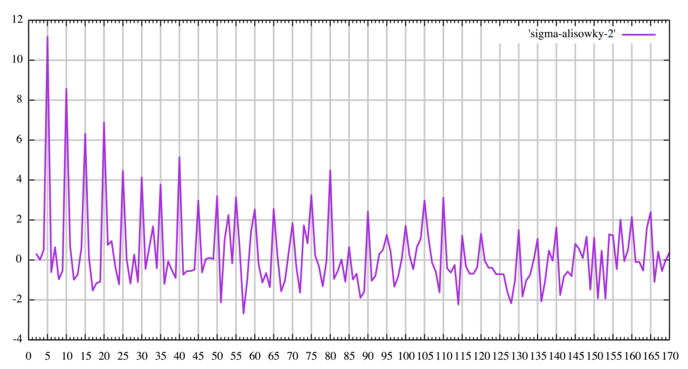
The peak is still at key length (5), with a smaller sigma of 11.2. Homophonic substitution does not seem to significantly obscure the resonance of the Vigenere key.
Bart, thanks for showing me the coincidence count method. Note that message 306 is a homophonic Vigenere made by glurk, and if you make a coincidence count chart, you will see that the keyword is length of 7. I sort of like that one, and wonder how it could be solved.
My plot confirms keyword length of 7 for glurk’s viginere+homophonic cipher:
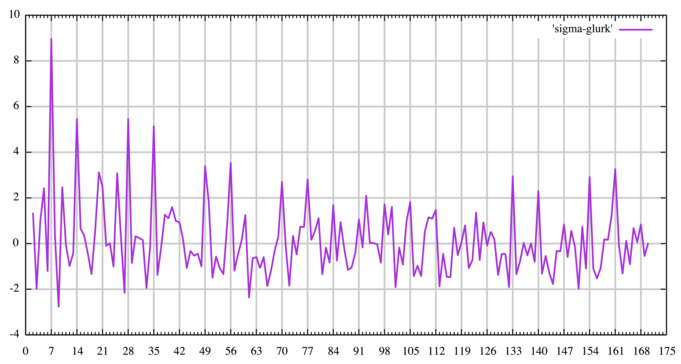
Peak sigma is 9.0 at width 7.
I’m very pleased with how clearly the key length shows up in the shuffle-based normalization of columnar IoC. Seems like a good candidate for a web-based tool, to supplement the traditional ways of finding the key lengths.
And also, based on these results, it seems unlikely the 340 uses vigenere, unless it’s in some different direction or it’s mixed up with some kind of transposition.
Peak sigma is 9.0 at width 7.
I’m very pleased with how clearly the key length shows up in the shuffle-based normalization of columnar IoC. Seems like a good candidate for a web-based tool, to supplement the traditional ways of finding the key lengths.
And also, based on these results, it seems unlikely the 340 uses vigenere, unless it’s in some different direction or it’s mixed up with some kind of transposition.
That is pretty definitive proof that there is no vigenere cipher below the homophonic layer.
I am impressed by the column ioc results and performance.
I will need to polish off my code for future.
Regards
Bart
Hi Smokie.
Sorry I missed this message.
I will try and answer and work through as soon as possible
Regards
Bart
I checked a block of messages from:
https://docs.google.com/spreadsheets/d/ … 1394933925
I started at message 91 and stopped at message 218. It was a convenient block of messages with 340 symbols. I may check some of the messages above, but a lot of them are of different lengths. Some of the messages in the block are multiobjective evolution messages, but I stopped at 218 when all below are multiobjective messages. There are a lot of different types of messages that I checked in the block, made by several different people to test a lot of different ideas.
Thanks for the reply. I figure we have taken it this far, so we might as well explore a few different directions. The message may not read from left to right, top to bottom. Zodiac put his signature at the bottom of the page, a circle with cross hairs. At times I have suspected that this might be a ruse.
Here is the 340, rotated 90 degrees to the right, and drafted into a 17 x 20 grid:
4 11 19 3 11 34 6 40 16 38 55 17 21 22 5 46 42
20 18 1 37 51 19 36 36 20 15 63 29 19 40 29 15 50
44 47 5 34 5 2 25 10 33 14 28 59 51 47 36 3 6
37 16 19 3 37 5 35 19 3 1 17 26 19 45 12 18 42
6 54 38 19 41 31 7 19 43 36 20 4 18 26 56 13 40
30 7 34 3 50 8 61 32 57 51 40 7 37 21 5 5 29
40 12 20 35 32 22 41 48 19 19 49 24 6 48 6 19 22
6 10 43 26 63 31 53 50 19 11 2 7 39 22 58 23 49
44 38 23 7 42 48 36 56 21 47 16 18 30 11 41 3 23
16 55 17 30 39 24 8 40 20 9 29 23 56 53 11 50 25
19 16 19 38 30 11 8 15 25 9 39 46 23 19 5 2 61
50 14 27 23 51 46 36 17 50 45 26 26 10 23 27 42 51
7 4 28 51 53 20 5 20 18 59 56 51 5 21 27 11 44
23 1 6 28 8 36 20 37 5 43 36 27 15 10 9 23 33
28 12 62 20 14 26 32 38 8 36 28 61 29 34 40 8 51
19 19 13 29 13 11 30 54 20 37 39 53 21 19 14 51 62
19 28 4 52 19 22 30 14 31 55 21 11 57 50 48 58 52
37 20 63 60 40 16 53 3 40 31 15 58 56 33 33 15 55
19 44 20 31 34 53 13 13 25 10 31 1 32 16 19 36 5
13 16 19 19 3 51 23 55 31 47 11 21 54 16 41 33 17
I found coincidence count spikes at 18, 36, and 108, all multiples of 9. Check it out.
Hi Guys. this is the 340 as a columnar scytale. out of curiosity can you run your checks on this. not sure which direction it should be read from. I am with you on the "ruse" bit smokie.
please note the top left hand column reading down, it peaked my interest. A,P,A,P,S,B,S,B.
ABCDEFGHIJKLMNHOL
PQDNBRSHTUVWMQSIX
AOYZaEbKcdBDeBfHB
PghDCBiGBjUEkLXlE
SmnKoUeIpqUSrHIIX
BsqoUfYktIjlSBQiu
SvVPwUxmWMEYLLNFV
BWOtyz0v12ZeKByoF
nJddeHk3YBBZD4Ukb
yjMyDr2LrOBVm1uwF
z0WwxFOcyePjGRKZO
BB5KWBZQk4BKQgQBL
vJ64FmlBaKfUHTqCy
ABGBia7HpzOjurnFj
JmljUXs5DvmP84Vhm
4iFXHopsjSERPDjUB
uKh9k3lqSr8DtbdSH
xLqdC!XDJ!DKN9ydF
FZ4RkL0MABXhNG2NO
HHL7xeknrjskjbSex
Here is the 340, rotated 90 degrees to the right, and drafted into a 17 x 20 grid:
I found coincidence count spikes at 18, 36, and 108, all multiples of 9. Check it out.
I ran my shuffle-based normalized columnar IoC on it – here’s the plot:

The positive spikes don’t stand out too much except for the one at width 145. But interestingly, there are negative spikes at widths 10, 20 and 40. I’m guessing it is to do with the low number of repeats in the first few lines of the top and bottom halves of the unmodified Z340 (which show up as columns when rotating by 90 degrees). Still, none of the sigmas are as significant as the ones that show up for ciphers that actually use vigenere+homophonic.
Hi Guys. this is the 340 as a columnar scytale. out of curiosity can you run your checks on this. not sure which direction it should be read from. I am with you on the "ruse" bit smokie.
Here’s my plot:
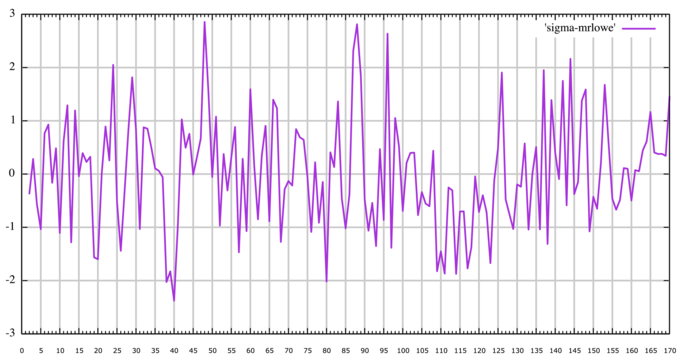
Not much to conclude from this – sigmas are rather low to be predictive of vigenere.
Thanks.
Because of the period 19 repeats, I don’t see it likely that there is a cipher step that diffuses the plaintext before homophonic encoding. Maybe there is, and I am going to keep looking. It is just very difficult for me to reconcile any diffusing cipher with the repeats.
I figure we have taken it this far, so we might as well explore a few different directions.
The message may not read from left to right, top to bottom. Zodiac put his signature at the bottom of the page, a circle with cross hairs.
At times I have suspected that this might be a ruse.
Might as well seem to have some momentum at the moment.
I assume someone has done a bi gram search to determine direction?
I found coincidence count spikes at 18, 36, and 108, all multiples of 9. Check it out.
Ha! here is another Coincidence. I’d be curious what you and Dave think of this.
The Keyspace for both have factors of 9 63(9×7) 54(9×6)
Here is the 340, rotated 90 degrees to the right, and drafted into a 17 x 20 grid:
4 11 19 3 11 34 6 40 16 38 55 17 21 22 5 46 42
20 18 1 37 51 19 36 36 20 15 63 29 19 40 29 15 50
44 47 5 34 5 2 25 10 33 14 28 59 51 47 36 3 6
37 16 19 3 37 5 35 19 3 1 17 26 19 45 12 18 42
6 54 38 19 41 31 7 19 43 36 20 4 18 26 56 13 40
30 7 34 3 50 8 61 32 57 51 40 7 37 21 5 5 29
40 12 20 35 32 22 41 48 19 19 49 24 6 48 6 19 22
6 10 43 26 63 31 53 50 19 11 2 7 39 22 58 23 49
44 38 23 7 42 48 36 56 21 47 16 18 30 11 41 3 23
16 55 17 30 39 24 8 40 20 9 29 23 56 53 11 50 25
19 16 19 38 30 11 8 15 25 9 39 46 23 19 5 2 61
50 14 27 23 51 46 36 17 50 45 26 26 10 23 27 42 51
7 4 28 51 53 20 5 20 18 59 56 51 5 21 27 11 44
23 1 6 28 8 36 20 37 5 43 36 27 15 10 9 23 33
28 12 62 20 14 26 32 38 8 36 28 61 29 34 40 8 51
19 19 13 29 13 11 30 54 20 37 39 53 21 19 14 51 62
19 28 4 52 19 22 30 14 31 55 21 11 57 50 48 58 52
37 20 63 60 40 16 53 3 40 31 15 58 56 33 33 15 55
19 44 20 31 34 53 13 13 25 10 31 1 32 16 19 36 5
13 16 19 19 3 51 23 55 31 47 11 21 54 16 41 33 17
Looks Like Dave has given this a poke so i will have a look at it in another way.
but first i need to convert this over to my own symbol space…
http://codepad.org/jWzF0pLp
I have been working on my own pseudo plaint text idea for a few weeks and have been meaning to start a thread on it but it needs a bit more research first to quantify its validity if any. Anyway might as well give it a bit of try now.
So now I take the key from z408 and apply it to your code. keep in mind some of the symbol key space is rejigged.
anyway.
TREGRCADRIPONLEYA LETHSEVVLAEPEDPAT AIECEENIHOTOSIVGA HREGHEREGTOEECFEA AKIEFSNESVLTEEFTD ONCGTBRDMSDNHNEEP DFLRDLFREEXLARAEL AISEESRTERENELONX AINNARVFNIREORFGN RPOOELBDLIPNFRRTN EREIORBANIEYNEEER TOUNSYVOTCEEINUAS NTTSRLELEOFSENURA NTATBVLHESVUAIINH TFWLOEDIBVTRPCDBS EETPTROKLHERNEOSW ETTRELOOSPNRMTROR HLESDRRGDSAOFHHAP EALSCRTTNISTDREVE TREEGSNPSIRNKRFHO
first pass looks like some words already in there.
out of interest i ran it throught my word searcher and it came up with 135 words over >= 3 chars
Dictionary Total lines 354986, Total search hits 135 ADRIP AIN AIS ALE ALS ANI ANT ANTA APE ARA BAN BANI BDL BVT CAD CEE CEE DIB DON DRIP EDP EEN EER EFS EFT ELA ELB EOF EOS ERE ERE ERE ERN ERNE ESD ETH ETHS EVE EXLA EYALET EYN EYNE FGN FREE GDS HAP HER HER HERE HERN HERNE HES HOT INN IRE ISE IST KIE KIEF KIEFS LAI LAR LEO LES LET LEY LIP LOE LOED LOO LOOS LSC NAR NEE NEE NEEP NEO NERE NIS NIST OOS ORB ORF OSI OTC PAT PATA PEA PEAL PEALS PED PON PSI RAN RANT REE REE REG REG REG REGR REGT REI REL REN REV REVE REVET RIP RLE RTE SAO SCR SEE SEE SEES SEN SIR STD TAI TAT TDR TEE TER TOE TOS TOU TREE TRP UNS URA URAN VET WET YALE
…we know that the use of KILL is likely.
So if we strip out all the other letters we end up with
........I...L... L.......L........ .I.....I.....I... ................. .KI.......L...... ................. ..L..L.....L....L .I...........L... .I.......I....... .....L..LI....... ...I.....I....... ............I.... .....L.L......... ......L......II.. ...L...I......... .......KL........ .....L........... .L............... ..L......I....... .........I..K....
So do a period search and see if we can find KILL…..And… no hits ![]()
But we have some hits for KIL and ILL
Searching for KIL Hit @ 20, mod 104 Hit @ 105, mod 104 Hit @ 190, mod 104 Hit @ 275, mod 104 Hit @ 37, mod 312 Hit @ 122, mod 312 Hit @ 207, mod 312 Hit @ 292, mod 312 Hit @ 139, mod 318 Hit @ 309, mod 318 Searching for ILL Hit @ 5, mod 4 Hit @ 90, mod 4 Hit @ 175, mod 4 Hit @ 260, mod 4 Hit @ 4, mod 8 Hit @ 89, mod 8 Hit @ 174, mod 8 Hit @ 259, mod 8 Hit @ 141, mod 57 Hit @ 67, mod 66 Hit @ 237, mod 66 Hit @ 315, mod 109 Hit @ 46, mod 186 Hit @ 216, mod 186 Hit @ 122, mod 206 Hit @ 292, mod 206 Hit @ 241, mod 273 Hit @ 65, mod 322 Hit @ 235, mod 322
Bugger practicalcryptography.com is not loading… I calculate a CHI squared = 67.063 and IoC = 0.073
The IoC is a little high but other wise not too far off a Chi of <100 i find is usually a good start.
However the homophonic substitution really messes things up.
Provided you assign the correct number of symbols to E T and all the others letters and the symbol frequencies are generally the same size you will alway get a good chi and IoC statistic. ![]()
Regards
Bart
I still wonder if there is any relationship to the period 19 or 39 repeats.
Here are the positions that are positive for both period 78 unigram repeats and period 19 bigram repeats. There are some interesting repeated patterns. And of the only 18 positions, 12 of them cover both the leftmost and rightmost period 78 repeat positions.
Check this out. On top are the period 78 unigram repeats. In the middle are the period 26 bigram repeats. On the bottom are the positions positive for both period 78 unigram repeats and period 26 bigram repeats. The interesting thing is that, almost all of them ( black bordered positions ), have BOTH the leftmost and rightmost of the period 78 unigram repeats.
Interesting observation, smokie. It is consistent with my earlier experiment which confirmed that the 78/26 combination produced the highest proportion of coinciding positions:
https://docs.google.com/spreadsheets/d/ … sp=sharing
(Hover over column headings for explanations)
I just added a column to indicate the greatest common divisor of the kasiski shift value and the period value. You can see that some combinations have a large common divisor.
TREGRCADRIPONLEYA LETHSEVVLAEPEDPAT AIECEENIHOTOSIVGA HREGHEREGTOEECFEA AKIEFSNESVLTEEFTD ONCGTBRDMSDNHNEEP DFLRDLFREEXLARAEL AISEESRTERENELONX AINNARVFNIREORFGN RPOOELBDLIPNFRRTN EREIORBANIEYNEEER TOUNSYVOTCEEINUAS NTTSRLELEOFSENURA NTATBVLHESVUAIINH TFWLOEDIBVTRPCDBS EETPTROKLHERNEOSW ETTRELOOSPNRMTROR HLESDRRGDSAOFHHAP EALSCRTTNISTDREVE TREEGSNPSIRNKRFHOfirst pass looks like some words already in there.
out of interest i ran it throught my word searcher and it came up with 135 words over >= 3 chars
Just for fun, I ran that plaintext through my fuzzy word searcher, which is basically an exercise in pareidolia. Each word is followed by the plaintext that closely matched it:
RABELAIS [RAELAIS] APPEALS [APEALS] TERENCE [TERENE] ENTRANT [ENURANT] FENELON [ENELON] [RENELON] TERPENE [TERENE] APPEAL [APEAL] REGERE [REGHERE] NELSON [NELON] ELAINE [ELAISE] PHOTOS [HOTOS] [IHOTOS] LARVAE [LARAE] AZRAEL [ARAEL] PETALS [PEALS] PEARLS [PEALS] REVERT [REVET] POOLEY [PONLEY] SERENE [ERENE] [TERENE] APIECE [AIECE] AISLES [AISEES] LOOSEN [LOOSPN] LIAISE [LAISE] PEDALS [PEALS] WETTER [WETTR] ELOISE [ELAISE] HERETO [HEREGTO] LAPPED [LAEPED] ORTNER [RTNER] [RRTNER] ELAPSE [ELAISE] BLAISE [LAISE] [ELAISE] RATNER [RTNER] [RRTNER] NEREIS [NEREI] [NEREIO] ORGANI [ORBANI] PATRIE [PATAIE] HEARNE [HERNE] PEDIAT [PEDPAT] RENDEL [RENEL] ELONEX [ELONX] REVERE [REVETRE] DALETH [ALETH] [YALETH] RIPPON [RIPON] PATTIE [PATAIE] VENIRE [VFNIRE] VENTRE [VETRE] GRANTA [RANTA] [URANTA] DURANT [URANT] [NURANT] NEREID [NEREI] [NEREIO] LAISSE [LAISE] [LAISEE] AHERNE [HERNE] [LHERNE] SVELTE [SVLTE] BREVET [REVET] [DREVET] SEGURA [SENURA] IPHOTO [IHOTO] EYELET [EYALET] ASNETT [ASNTT] OSSETT [OSWETT] ARABEL [ARAEL] ETTORE [ETTRE] ENTREE [ETREE] LIERNE [LHERNE] BEANIE [BANIE] APPALS [APEALS] POTOSI [OTOSI] [HOTOSI] SORTER [SRTER] LETTRE [ETTRE] [WETTRE] TAISCE [TAIECE] LSRAEL [LARAEL] BRANTA [RANTA] [URANTA] CONLEY [ONLEY] [PONLEY] URANIA [URANTA] METTRE [ETTRE] [WETTRE] ERENCE [ERENE] RELAIS [ELAIS] [AELAIS] [RAELAIS] SIRNAK [SIRNK] LHERBE [LHERNE] PARTAI [PATAI] EXTREE [ETREE] SENORA [SENURA] THERE [HERE] [TERE] [GHERE] [TNERE] THESE [THSE] THOSE [THSE] THREE [TREE] WHERE [HERE] [GHERE] NEVER [NEEER] OFTEN [OFSEN] LARGE [LARAE] VOICE [VOTCE] SEEMS [SEES] LEGAL [LEYAL] EVENT [EVET] RULES [RHLES] PIECE [IECE] [AIECE] LOOKS [LOOS] TREES [TREE] [TREEG] [TREEGS] SHAPE [HAPE] [HHAPE] URBAN [RBAN] [URAN] [ORBAN] RAISE [AISE] [LAISE] INNER [INNAR] SHEET [SEET] TOWNS [TOUNS] DROVE [DREVE] DRIVE [DREVE] STORE [STDRE] SCOTT [SCRTT] SWEET [SEET] [SWET] [SWETT] GRANT [RANT] [URANT] HASNT [ASNT] [UASNT] ROLES [RHLES] LOVED [LOED] HOLES [HLES] LAURA [LARA] MEALS [EALS] [PEALS] ARISE [AISE] LOOSE [LOOS] [LOOSP] SEEKS [SEES] ORGAN [ORBAN] LOYAL [LEYAL] NERVE [NERE] SEEDS [SEES] SANTA [ANTA] [RANTA] THEFT [TEEFT] PHOTO [HOTO] [IHOTO] DEALS [EALS] [PEALS] ELLIS [ELAIS] SWEAT [SWET] [SWETT] ANNIE [ANIE] METRE [ETRE] [VETRE] SWEPT [SWET] [SWETT] REBEL [RENEL] PEAKS [PEALS] POOLE [POOE] [PONLE] PENAL [PEAL] SEXES [SEES] ALERT [ALET] ISLES [ISEES] LEITH [LETH] FINES [FSNES] NYLON [NELON] TOURS [TOUNS] TWIST [TNIST] IRENE [RENE] [ERENE] PASTA [PATA] NEWER [NEEER] STARE [STDRE] FREED [FREE] [FREEX] RENAL [RENEL] NIECE [IECE] [AIECE] AISLE [AISE] [AISEE] ETHOS [ETHS] SEALS [EALS] [PEALS] PEARS [PEALS] RENEW [RENE] [RENEL] EXERT [EERT] [EEERT] CLARA [LARA] [XLARA] NOTTS [NTTS] ELTON [ELON] PEARL [PEAL] ELVIS [ELAIS] LOOPS [LOOS] ERECT [EREGT] NOUNS [OUNS] [TOUNS] SIREN [SIRN] PEDAL [PEAL] OTLEY [ONLEY] RIPON [RIPO] [IPON] [DRIPON] [RIPONL] FREER [FREE] [FREEX] LEAFS [LEOFS] REEFS [REEGS] METRO [MTRO] HORNE [HERNE] LAPSE [LAISE] RANGA [RANTA] SPERM [SPNRM] HEERE [HERE] ANITA [ANTA] MELON [ELON] [NELON] REEDS [REEGS] ANILE [ANIE] ARTAI [ATAI] RAHEL [RAEL] ERNIE [ERNE] LUISE [LAISE] EARLS [EALS] SNAPS [SNPS] TUNIS [TNIS] [TTNIS] APNEA [APEA] LOGOS [LOOS] ARIEL [ARAEL] ELISE [ELAISE] LARNE [LARAE] HERON [HERN] ETHER [EGHER] ANGIE [ANIE] CAPRI [CADRI] TANTA [ANTA] [RANTA] GRENE [RENE] [ERENE] REINO [REIO] TERSE [TERE] LARVA [LARA] RENFE [RENE] LOOMS [LOOS] JAHRE [AHRE] [GAHRE] ELLOS [ELOOS] ALEUT [ALET] PETAL [PEAL] EBERT [EERT] [EEERT] SELES [SEES] ARNIE [ANIE] FRERE [FREE] REEVE [REVE] EBENE [ERENE] OLSEN [OFSEN] REPEL [RENEL] KANTA [ANTA] [RANTA] RENCE [RENE] TUNER [TNER] TONER [TNER] FREES [FREE] [FREEX] REELS [REEGS] CADRE [CADR] [CADRI] LOCOS [LOOS] TROLL [TROKL] RAVEL [RAEL] LOBED [LOED] SERES [SEES] HEEFT [EEFT] [TEEFT] TIERE [TERE] [TNERE] PETRO [PTRO] REVUE [REVE] LAPIS [LAIS] RIPEN [RIPON] VALET [ALET] [YALET] RALES [RHLES] BERNE [ERNE] [HERNE] IDEES [ISEES] HEURE [HERE] DURAN [URAN] [NURAN] NITRE [NIRE] LETTS [LETHS] SEDES [SEES] PATAI [PATA] [ATAI] [DPATAI] [PATAIE] AKELA [AELA] TAPIE [TAIE] RESET [REVET] AREAL [APEAL] PINNA [INNA] [AINNA] FIEFS [IEFS] [KIEFS] AURAE [ARAE] VOLTE [VLTE] SLEET [SEET] REVEL [REVE] [RENEL] [REVET] ADRIA [ADRI] [ADRIP] HALES [HLES] TAINE [TAIE] DRIPS [DRIP] [DRIPO] ELDON [ELON] ATARI [ATAI] SENSU [SENU] LARUE [LARAE] DEREN [EREN] [TEREN] PONCE [PONLE] FELON [ELON] [NELON] ESHER [EGHER] MARAE [ARAE] [LARAE] PATAN [PATA] [PATAI] REINE [RENE] HEINE [HERNE] AVISE [AISE] HERNE [HERE] [HERN] [ERNE] [LHERNE] [HERNEO] WOOED [WLOED] DBASE [DBSE] PETRE [ETRE] [VETRE] INCAS [INUAS] HEARN [HERN] RETRO [RMTRO] LOPED [LOED] TITRE [TTRE] SEERS [SEES] ELTIS [ELAIS] SAEPE [AEPE] [LAEPE] MINNA [INNA] [AINNA] ARABE [ARAE] VERNE [ERNE] [HERNE] PATTI [PATAI] SORTE [SRTE] TERES [TERE] [TEREN] PEATS [PEALS] ESTER [ESRTER] EPRDF [EPDF] RIVET [REVET] ADELA [AELA] TIREE [TREE] ONTOS [OTOS] JANIE [ANIE] [BANIE] SETTS [SNTTS] LOWED [LOED] PEELS [PEALS] ENGEL [ENEL] NEHER [NEEER] TOUTS [TOUNS] NEGER [NEEER] OTROS [OTOS] DANIE [ANIE] [BANIE] PSION [PSIRN] RDBMS [RDMS] EALES [EALS] REVIE [REVE] ANTAL [ANTA] [ANTAT] CERTO [ERTO] [EERTO] SWETE [SWET] [SWETT] REGNE [RENE] [REGHE] EVERT [EERT] [EVET] [EEERT] TOSHI [TOSI] TERRE [TERE] PONTE [PONLE] HEALS [EALS] [PEALS] LETHE [LETH] [LETHS] [LETHSE] NIREX [NIRE] [NIREO] AGLET [ALET] WEALS [EALS] [PEALS] LOBOS [LOOS] BRANT [RANT] [URANT] SEEPS [SEES] LYETH [LETH] WETTE [WETT] [WETTR] [WETTRE] TERED [TERE] [TEREN] NEEPS [NEEP] [NEEPD] NERVI [NEREI] RENEE [RENE] [RENEL] CHERE [HERE] [GHERE] ESTRE [ETRE] [ETTRE] ALTAI [ATAI] DELON [ELON] [NELON] POWEL [POOEL] JURAN [URAN] [NURAN] VIREO [IREO] [NIREO] INCAR [INNAR] ENERO [ENELO] FREIE [FREE] ISTER [ISTDR] NEONS [NEOS] LATHS [LETHS] POPLE [PONLE] CERNE [ERNE] [HERNE] PEALS [PEAL] [EALS] [APEALS] [PEALSC] HEARE [HERE] METHS [ETHS] [LETHS] EDALE [EYALE] FAIRE [FNIRE] NEUER [NEEER] GREVE [REVE] [DREVE] OXLEY [ONLEY] ETTER [ETTR] SEEIN [EEIN] [CEEIN] ANTAR [ANTA] [ANTAT] ELSON [ELON] RANTS [RANT] [RANTA] LOTOS [OTOS] [LOOS] [HOTOS] BTREE [TREE] [ETREE] TRIST [TNIST] TYREE [TREE] GEERT [EERT] [EEERT] TRANT [RANT] [URANT] KEREN [EREN] [TEREN] LYRAE [LARAE] QURAN [URAN] [NURAN] PATNA [PATA] SCUTT [SCRTT] SEEST [SEES] [SEET] [SEESR] [SEESRT] VENIR [VFNIR] ANIME [ANIE] REAVE [REVE] KLARA [LARA] [XLARA] PACTA [PATA] RANTE [RANT] [RANTA] SHERE [HERE] [GHERE] POORE [POOE] ERATO [ERTO] SENOR [SENUR] ELLON [ELON] LAIUS [LAIS] LONGA [LONXA] BEALS [EALS] [PEALS] CORBA [ORBA] [IORBA] CINNA [INNA] [AINNA] REGER [REGR] [REGHER] FREGE [FREE] EXPED [EPED] EXPAT [EDPAT] APPAL [APEAL] GELON [ELON] [NELON] HEYNE [EYNE] [IEYNE] [HERNE] NIHON [NIHO] [NIHOT] RENTE [RENE] SNIPS [SNPS] REEKS [REEGS] REALS [EALS] [PEALS] EGTON [EGTO] [EGTOE] RASTA [RANTA] TENER [TNER] NEARE [NERE] SINES [SNES] TURAN [URAN] [NURAN] ERENT [EREN] [EREGT] [ERENE] SIRTE [SRTE] REXEL [RENEL] TROTH [TRORH] EIGHE [EGHE] NASIR [NPSIR] NARVA [NARV] [NARVF] ANTEA [ANTA] SWETT [SWET] [WETT] [OSWETT] [SWETTR] REIHE [REGHE] BORBA [ORBA] [IORBA] LAINE [LAISE] LOONS [LOOS] MANIE [ANIE] [BANIE] MATAI [ATAI] [PATAI] RELET [REVET] TREED [TREE] [TREEG] SELON [ELON] [NELON] ANTIA [ANTA] TERAN [TEREN] DIATA [DPATA] LAIRS [LAIS] ENTEL [ENEL] LARGA [LARA] ARVIN [ARVFN] ECAFE [ECFE] SUTER [SRTER] SEETH [SEET] [SEETP] TYNER [TNER] REGIO [REIO] [REGTO] ORMAN [ORBAN] HILES [HLES] RABTA [RANTA] EOYAL [EYAL] DINNA [INNA] [AINNA] EDINB [EDIB] LAMPE [LAEPE] AHERN [HERN] [LHERN] NEERE [NERE] [NEEE] HERVE [HERE] [HERNE] CETIN [CEEIN] AIMEE [AISEE] MALET [ALET] [YALET] SKEET [SEET] ELGON [ELON] PATRI [PATAI] RESTO [REGTO] BASIE [BANIE] ADLAI [AELAI] ENLAI [ELAI] ANISE [AISE] [ANIE] SOTER [SRTER] VERRE [VETRE] RECTO [REGTO] EVETT [EVET] [EVETR] XTREE [TREE] [ETREE] TOONS [TOUNS] NEOTS [NEOS] NEELD [NEEPD] ENTRE [ETRE] [ETTRE] AISNE [AISE] [AISEE] PLATA [PATA] OLLEY [ONLEY] WANTA [ANTA] [RANTA] WASNT [ASNT] [UASNT] SEGUR [SENUR] AELIS [AELAIS] NUTTS [NTTS] NURIA [NURA] SWETS [SWET] [SWETT] ANDIE [ANIE] RECOR [REOR] [REIOR] TWERE [TERE] [TNERE] OFFEN [OFSEN] TOPEE [TOEE] NUMAN [NURAN] POOEY [POOE] [POOEL] HERES [HERE] [HEREG] HERED [HERE] [HEREG] MANTA [ANTA] [RANTA] ELENI [EENI] BRIMS [BRDMS] TROOL [TROKL] ALEPH [ALETH] LESER [LESDR] KIEFT [KIEF] [KIEFS] PCDOS [PCDBS] HARPE [HAPE] EGGER [EGHER] LIETH [LETH] AMELA [AELA] REGEL [RENEL] ORHAN [ORBAN] ORLAN [ORBAN] RATER [RTER] TERME [TERE] LASSE [LAISE] ENURE [ENUR] [ENURA] POELE [PONLE] CADER [CADR] HERRN [HERN] ARWEL [ARAEL] ERANT [RANT] [URANT] ZOTOS [OTOS] [HOTOS] ARMEL [ARAEL] SKETT [SWETT] PARTA [PATA] PATRA [PATA] PAISE [AISE] [LAISE] BANDE [BANIE] SEEER [EEER] [SEESR] [NEEER] TANIS [TNIS] [TTNIS] URALT [URANT] REGIE [REGHE] REGNO [REGTO] ELVET [EVET] RABAN [RBAN] BEREN [EREN] [TEREN] DILIP [DLIP] TOSTI [TOSI] NELLO [NELO] NEPOS [NEOS] OGLEY [ONLEY] NEGRE [NERE] EETPU [EETP] [EETPT] EEVIN [EEIN] BLOOS [LOOS] [ELOOS] CESEN [CEEN] ERENS [EREN] [ERENE] HOLOS [HOTOS] ARTER [RTER] [SRTER] AIKIN [AIIN] RILES [RHLES] PEALE [PEAL] [PEALS] VOTRE [VOTCE] [VETRE] DAPAT [DPAT] PERLS [PEALS] ARAKI [AAKI] GADRE [GAHRE] ETTLE [ETTRE] BREVE [REVE] [DREVE] BANTA [ANTA] [RANTA] NOIRE [NIRE] ATAIE [ATAI] [TAIE] [PATAIE] [ATAIEC] TINER [TNER]
Here is another perspective of the period 78 unigram repeats and period 26 bigram repeats:
The period 26 bigram repeats are on a period of 78. They are pairs of identical bigrams set apart by a period of 78.
Red: Backwards D and G are period 26 bigrams, and there are two of them. They are spaced at a period of 78.
Green: Backwards P and backwards C are period 26 bigrams, and there are two of them. They are also spaced at a period of 78.
Purple: + and + are period 26 bigrams, and there are two of them. They are also spaced at a period of 78.
Blue: The left half filled circle and the vertical line are period 26 bigrams, and there are two of them. They are also spaced at a period of 78.
They are period AX period X bigram repeats where A is a multiplier of X!




