O.k., I will put something together hopefully within days, maybe a little more.

I made a huge spreadsheet with the 111 messages that you posted a few days ago, and I can select which message to analyze by changing the value in one cell. I also re-tooled one of my spreadsheets so that it shows the period x repeats and then only the diagonal rows where there are at least three positions highlighted.

I want to see if I can detect a large geometric shape route transposition versus a transposition of smaller message chunks or no transposition at all. I checked a few of your messages, and there are some very interesting patterns that develop. Below is message 3. On the left are all of the period 19 repeat positions, and on the right only diagonal rows with at least three positions. Some of the messages have a lot more, but I am showing this one because of the interesting patterns.

My comparisons will include stats for period repeats, count of positions, count of positions in diagonal rows of three or more, and Kasiski spike x and y values.

Looks good so far. I look forward to seeing more of what you find!

I am going to add one more thing to my search. Wondering if the cipher increases the probability of pivots, I think I will compare the period 1 bigrams with the period 17 bigrams, looking to see if there are repeats.

Here is a summary of some stats for the 111 messages. I don’t know what type of cipher these messages were generated from, and have not tried to solve any of them.

Top is a distribution of the count of period 19 repeats. X axis is the count of period 19 repeats, and y axis is count of messages with that many repeats. The spreadsheet found 67 for the 340, which I marked in red, and more messages have 67 repeats than any other count of repeat.

Bottom is a distribution of the count of positions that are included in diagonal rows of at least three positions. The idea was to develop a way to distinguish one big route transposition from transpositions in smaller plaintext chunks ( e.g. bifid or railfence) or a message with no transposition at all. X axis is count of positions, and y axis is the count of messages with that many positions. The 340 has 61 positions, marked in red. But many of the messages have a lot more. If the messages are not big route transpositions or scytale, then the idea didn’t work.

What cipher did you use to generate the messages? If the messages were scytale, then this doesn’t tell us much. But if the plaintext are not transposed, then that tells us that the test may not be useful. Not sure.

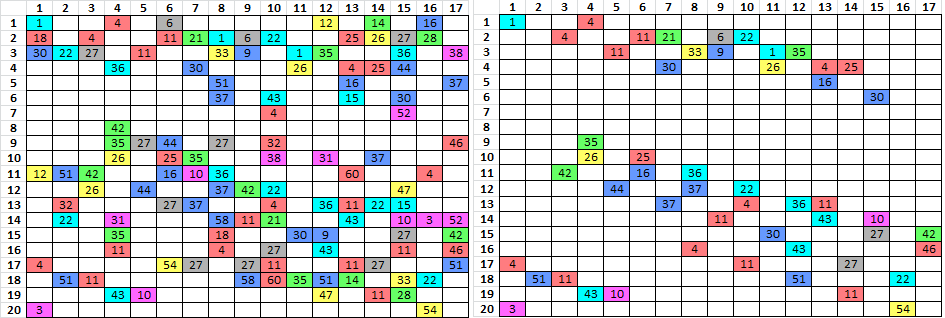
I also had an idea that was a bit crude. I was wondering if I could test a cipher for a propensity to generate pivots. I placed two of the same messages side by side. For the message on the left, I made a list of all period 1 repeats. For the message on the right, I made a list of period 17 repeats. Then, I cross checked the lists. I highlighted all of the positions on the left messages that were period 1 repeats and the same symbols showed up on the list of period 17 repeats. Then I did the same with the message on the right, highlighting positions of period 17 repeats where the same symbols showed up on the list of period 1 repeats. And I did the same thing for period 2 compared with period 34. I totaled all of the positions. See example below.

On the top, x axis is the number of positions ( rounded to the nearest increment of 10 ), y axis is the count of messages with that count of positions. Not sure if the cipher was designed to generate pivots, or how useful this test is. The Z340 had 340 positions highlighted between all of the spreadsheets, marked in red.

On the bottom, x axis is coincidence count spike y value. The y value is the count of messages with that x value. The 340 spike was at x = 78; y = 18, marked in red. Maybe the only interesting result from all of the stats is the fact that 6 of the messages had spikes higher than 18, and that is consistent with the former examination where I found 9 messages out of 128. Coincidence count spikes do happen, with 15 messages out of 239 total ( 6% of the time ).

I will take a look at the following high CC spike messages for divisor repeats:

8, 11, 19, 35, 48, and 83.

Smokie, thanks for the analysis. Those 111 ciphers are regular monoalphabetic homophonic substitution, with no transposition. Here are the same ciphers in the feature explorer tool: http://zodiackillerciphers.com/hypothes … dex-1.html

It is interesting that the phenomena of sequential period 19 repeats (i.e., your consecutive diagonal bigrams at period 1) does not seem to be a result of transposition, and seem to occur quite naturally. However, my cipher generator forces the search towards symbol assignments that achieve the same period 19 phenomenon that we see in Z340. So it’s not a really natural way for the period 19 thing to arise. Which cipher schemes naturally produce spikes in periodic bigram? I think the best way to answer that is to get a big cipher library, and encipher lots of random plaintext with it (with randomly selected parameters). Then measure how often the odd phenomena like bigrams, pivots, even/odd bias, etc. can be found in the cipher texts of each scheme.

BartW pointed out this library to me: https://github.com/WilliamMason/crypto-py It has encode/decode support for very many pen+paper cipher schemes used by the ACA.

So many experiments, so little time.

I finished my search for bigram x repeats where x is a divisor of the coincidence count x value. Five of the six messages that have a CC spike over 18 have them, and strangely, the CC spike x value is 81 for three of them.

Top row in red is the message number. And I shaded light blue the bigram repeat divisor periods. For example, look at messages 8 , 11, and 35. The CC spike x value is 81, and the divisor bigram period is 27. Message 8 has two, message 11 has three, and message 35 has four! Are they the same plaintext?

And here are a couple of examples. For messages 11 and 35, the divisor is 27 and the CC x value is 81. But the repeat positions are different.

So, it can happen with a no transposition all homophonic substitution message. Maybe about… 5% to 8% of the time!

I post this here for completeness.
I recently came across some loose observations that vaguely implied a right to left, top down writing of the plaintext.
Due to the previous seen pronounced Kasiski but abnormal spectrum I had hoped to finally observe a typical spectrum however this was not the case.
also preforming a DFT on the data proved unhelpful
Regards
Bart

Reversed data

16,15,14,13,12,11,10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0,
32,31,30,29,28,27,26,25,24,23,22,21,20,19,18, 4,17,
40, 0,39,21,12,32,20,25,14,38,37,18,36,35,34,33,19,
15,30, 2,18,18,22, 4,44, 7,29,43, 5, 6,42, 4, 4,41,
53, 9,52,51,18, 8,50,49,10,16,48,47,39,18,36,46,45,
20,24,15, 3,50, 9,55,16,29,54,22, 5,50, 6, 2,43, 4,
10,12,39,27, 7,14,58,35,37,15,57,23,56,30,18,49,21,
46,12,59,18,39,26,17,45,18,22,21,48,31,40,15,14,20,
30,52,62,61,33,35,19,50,15, 2,38,18,60,18,36,28,16,
54,33,19,50,28,42, 4,22,18,40, 6,18, 7,37, 5,39,54,
22,30,36,13,60, 4,19,26,24,10, 1,47,49,53, 2,18,37,
50,19,51,18,27,36,52,13,49,29,10,40, 2, 5,35,28,15,
 2,43,57,20,35,19,50,49,10,17,18,21,33,41,46,62,39,
18,18,47,52, 7,35,27,60,52,15,49,31, 6,17,50,14, 5,
18,54,49,38,37, 7, 3, 1,55,46,52,34,29,11,58,19,33,
15,14,56,36,31,27, 6, 4,22,20,30,19,39,44,27,35,10,
12,32,10,19,25, 5,50,18,28,55,62,11,12,18,13,35, 2,
 4,32,20,53,13, 0,41,22, 8,35,25,39,55,25,32,18,18,
35,55,54,29,19,22,26,45,19,47,42,28,25,16, 9,50,10,
18,57,30,10,61,43,22,38,39,41, 9, 4,17, 0,24,36, 3

I’m not sure if it is related but Glenn Claston mentions an IoC spike at 78 here http://www.zodiackiller.com/mba/zc/69.html

Bert,

I actually did look at repetition rates among many other things, and if you’ll check my old posts you’ll see that I’ve been arguing for awhile that there are very few differences between the 408 and 340-ciphers. Your illustration is a very good one and a very good addition to the already overwhelming evidence that the 340 is probably a homophonic cipher or some variant.

———————————–
By rows
408-cipher: 7% = 27 reps /(24*17)
340-cipher: 6% = 19 reps /(20*17)

By columns
408-cipher: 17% = 71 reps /(17*24)
340-cipher: 16% = 55 reps /(17*20)
———————————–

Your figures above are accurate, and you’ll notice that in every measure of repetition the 340 cipher rates lower than the 408. The extra characters don’t add the extra necessary to make up the diffenerence either. Something is causing this, and as you’ve stated, transposition makes no difference in the counts, so it must be something else.

Every check I’ve made for transposition comes up negative, which is disturbing in light of all the other evidence that makes this an unsolved homophonic substitution cipher. Group repetitions and characters at distances all appear to be linear and written left to right. I’ll make a chart of percentages on these figures compared to the 408 and post it.

Behavior(1): *Within* each cipher, the rep rate in rows is
notably less than the rep rate in columns (6-7% << 16-17%).

Behavior(1) is consistent with homophonic substitution,
possibly combined with transpositions of some kind.
(The transpositions would have no affect on the rep rates).
It would be a natural consequence of deliberately suppressing
(on avg) the short-term repetition of characters at the time
the ciphertext substitutions are being made. This would
reduce the row rates but would have much less affect on
column rates, which depend on column alignments that are not
likely to be controlled. On the other hand, isn’t this
behavior very unlikely with just about any other substitution
scheme (e.g. polyalphabetic)?

Unlikely with a textbook polyalphabetic, but try a low-level polyalphabetic using the keyword “Abracadabra” for instance. It generates roughly the same statistics as a homophonic substitution cipher, especially in conjunction with randomly selected character alphabets. Too tricky for Zodiac? Not if you consider using the repetition “slavesslavesslaves” or something similar. This was the angle of my investigation into polyalphabetics in the 340. Unfortunately the statistics nixed the idea just about as soon as I came up with it!

Behavior(2): *Between* ciphers, the rep rates are practically
the same, by row (6% ~= 7%) and by column (16% ~= 17%).

Behavior(2) seems to strongly indicate that the type of
substitution scheme used in the 408-cipher, i.e. homophonic,
was used again in the 340-cipher. (And again this behavior
would not be affected by combining the substitution with
transpositions. Also, it seems to me that the addition of
some transpositions would be sufficient to account for the
fact that the 340-cipher has not yet been solved.)

Doesn’t it seem likely that the rep rates would have changed
significantly by any fundamental change in the substitution
scheme (e.g. switching from homophonic to polyalphabetic)?

In a "Paradice Slaves" thread, you mention some results of
chi^2 & IoC tests performed on the 340-cipher alone. It might
be interesting to see how those compare *between* the two
ciphers.

I’ve run the IoC tests on both ciphers and there is nothing to compare the two against. The 408 has random peaks as a result of the language used, while there are some lower peaks in the 340, none matching each other. The 340 has an extremely high peak at 78 (13×6, 26×3) which I am checking out through other means (still only 5.5%, but much closer to 6.8 than any peak in the 408). It might be of some significance if we figure the Paradice Slaves cross to be of 13 characters instead of 14, the “a” being used twice in each word. How it could be used is still a mystery however.

I’m glad you’re looking at this cipher, and it seems you’re interested enough to have come up with your own transcription. How does your transcription compare to mine? Do I have any mistakes I need to look at?

Hi Jarlve,
Thanks for the link. I am not familiar with this material so i will have a read.
I am trying to get my head around your other posts as well at the moment.

Regards
Bart

I was commuting to work this morning and had an idea. Draft a 338 letter message LRTB into a 26 x 13 rectangle, and encode with a 6 letter long Vigenere key LRTB. Then read off the letters TBLR and transcribe { EDIT: LRTB } into a 17 x 20 rectangle. Then encode with an inefficient homophonic key. This should produce period 78 unigram repeats. I said before that I couldn’t see how it would create period 19 bigram repeats, earlier in this thread. But I wonder if generating a lot of messages with a homophonic key that maps all 26 letters would create more frequent false positive period x bigram repeat spikes.

EDIT: I counted 2173 period 6 unigram repeats in all 100 of Jarlve’s plaintext messages. So that is an average of 22 for each message. The letter E is most frequent, coming in at 502 of the 2173.

Perhaps some variation of this could create a lot of period 39 repeats and pivots. Maybe with a certain type of six letter keyword.

Then untransposing the TBLR would reveal a keyword length of 6, not? Have you checked that?

I am going to right now.

Here is the 340 untransposed LRTB at period 13.

1 14 26 19 5 3 51 23 19 13 27 3 38 55 61 50 34
6 53 2 20 36 11 42 43 25 58 2 15 27 38 5 31 9
55 31 11 40 16 8 38 14 14 22 15 48 4 31 14 33 1
48 1 19 3 16 28 39 43 16 19 30 57 21 19 51 19 19
37 53 19 51 19 8 21 19 13 14 20 18 4 17 29 15 7
46 52 17 24 15 60 20 7 3 31 37 18 18 19 38 23 13
19 54 46 5 5 18 30 26 6 47 53 56 58 16 13 36 41
54 23 28 11 7 34 39 5 12 19 21 27 10 6 5 31 21
44 37 10 10 16 41 47 34 19 50 16 19 50 32 20 50 7
63 33 33 23 42 7 19 32 33 30 19 54 51 38 32 17 62
23 48 29 52 51 50 59 55 28 56 26 5 20 40 8 20 33
13 8 40 5 4 36 49 29 63 5 2 36 20 20 16 12 19
32 29 56 11 30 39 9 21 20 22 45 48 44 16 59 22 37
53 43 11 6 51 36 53 30 11 37 19 40 51 55 23 10 22
34 40 5 49 3 25 15 23 19 31 29 25 3 40 21 61 35
36 57 51 26 10 56 44 11 23 35 1 23 17 7 21 8 19
61 55 51 27 41 63 58 28 53 28 15 6 36 17 36 62 12
24 36 41 19 11 51 22 28 46 19 40 20 20 11 47 44 36
47 45 16 26 9 26 4 11 13 25 37 42 19 50 6 50 40
18 39 6 34 5 30 42 3 8 56 40 3 20 23 29 37 31

It moved the spike to a period of 6. There are not a lot of other little spikes at multiples of 6 though, except period 72.

Hey smokie,

I have updated AZdecrypt (1.04) and its thread with a vigenère solver available for download. You should be able to explore the hypothesis now.