Evaluation II

Focussing specifically on the key that would be required to match the proposed joint solves for the Z13 and 32 above this would, possibility only in part (was a full key created, even for letters that weren’t used in either of the ciphers?), be as below:

Comparison with the keys for the previous two ciphers — the Z408 and the Z340 — shows that, excluding the three unique symbols that were apparently intentionally introduced to some purpose specifically for the Z13/32, all the remaining symbols are found within the key for the Z340, without exception. That is, there are none from the set of symbols that occur in the key for the Z408, but not in that for the 340. There are, however, some (e.g. ‘C’, ciphertext) that are found in the Z340 alone.

This is merely noted, and it’s not clear if there is any significance to be drawn from this given that what we are working with may only be the key in part.

As to seeking and evaluating potential support for the proposed solution here, however, the following is worth spending a little time pursuing as, if present, it would provide high-level evidence of the solution being essentially correct. (We cannot expect it to be present, all the same, but will look anyway.)

In this evaluation we are looking, then, to test whether there is any clear evidence of the proposed Z13/32 key being such as can be shown to be derived from that of the Z340 according to some clearly intentional and precisely defined method. If such evidence is present, and with the derived key reproducing the same plaintext we have arrived at by another route, then we have much indeed. If, on the other hand, we can find no direct support for any concrete relation between the keys for the Z340 and the Z13/32, then we have nothing at all.

By way of a spoiler, at this point it would seem that the latter is by far the likeliest outcome. That said, I shall note just a few observations that stand out, but are nonetheless of dubious significance.

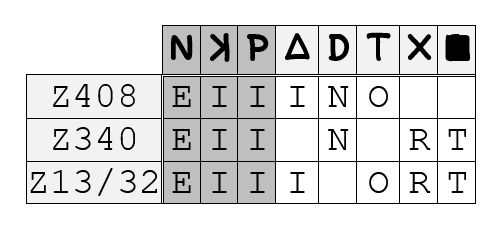
A comparison of the two part-keys, as they relate to the plaintext offered for the Z32, is given below:

From this comparison, then, perhaps the first point to merely note is that, where the proposed plaintext of the Z32 requires a minimal key covering 15 distinct letters, the actual symbols used as they are found in the key for the Z340 derive similarly from a subset of the latter corresponding to 15 distinct letters. It does not, at this time, appear possible to propose whether there is any significance to this observation or not, and it is noted here just for completeness.

The next point of note, then, is the presence of a number of instances of the same symbol being used for the same letter across the two keys, and these amount to 5 out of 29 common symbols:

• ’N’ encodes ‘E’ in both;
• reverse-‘K’ encodes ‘I’;
• ’P’ encodes ‘I’;
• ’X’ encodes ‘R’; and
• filled-square encodes ‘T’.

Further to these, but again of unclear relevance, it is observed also how, of the three shared symbols encoding ‘T’ in the Z340, one (filled-square) stays with ‘T’ in the Z13/32 key, one (half-filled square) is shifted immediately left to encode ‘S’ and one (‘G’) is shifted immediately right to encode ‘U’.

Other patterns may be noted also. For instance, if we consider the five symbols from the Z340 used to encode the letter ‘N’ in the Z13/32, we may observe the following: that, starting with the cipher symbol ‘W’ as encoding ‘W’ itself in the Z340, if we proceed along the ordered plaintext letters for the Z340 part-key to the right, with wrapping, we find that picking a symbol from every other subsequent column will gather the full five — ‘W’, ‘K’, ‘A’, ‘F’ and ‘H’.

What is absent overall, however, is evidence of any one particular method of (say) transposition being used consistently across the keys as a whole. And without that, as noted above, we essentially don’t have anything from this evaluation, at least to this point.

Posted by: @shaqmeister

What is absent overall, however, is evidence of any one particular method of (say) transposition being used consistently across the keys as a whole. And without that, as noted above, we essentially don’t have anything from this evaluation, at least to this point.

So, in comparison with the rather pessimistic conclusion required of this particular evaluation thus far, focussed as it is upon a comparison of keys between the proposed Z13/32 solution and the Z340, the following would indeed appear to turn all this around and present an observation of plausibly very high significance.

Recall how, in the previous post, the proposed Z13/32 key was directly compared to that of the Z340 to identify 5 cipher symbols encoding the same plaintext letter in both. Here, then, let’s extend this and do the same through a comparison of the Z408 key with that of the Z340 and, again, of the Z408 with the Z13/32. The results of these three comparisons together are then found to be as in the following figure (columns ordered alphabetically on plaintext):

And this result can surely only be interpreted as far from insignificant.

In short, whereas there are found to be 5 common symbol encodings between the Z340 and the proposed Z13/32, 4 common symbol encodings between the Z340 and the Z408 and 5 between the Z408 and the Z13/32, there are included in these three which are evidently persistent across all the keys. And this, to my thinking, is hardly consistent with anything we might expect from chance.

This would appear particularly significant as the ’E’ and the ’I’ are just those very letters that duplicate (in plaintext) through, and link together, all of the key words of ’EIGHT’, ’SIGNS’, ’NE’ and ’GEMINI’, providing all of the vowels present across all of them.

Thus, if you were somehow to be aware of these three pervasive repeats from the start (which is hypothetical, of course, as knowledge of their carrying through all of the ciphers would require actual solving of the last two, as here), and then if you were to merely apply the assumptions set out in the first post of this thread, then you would basically have everything you need to solve all but the range in the Z32. ‘EIGHT’ at the start of the 32 is now trivial. Eight what? ‘SIGNS’ completes ‘NE’ in the 13. ‘GEMINI’ remains as all but given, unless you want to explore ‘MEDICI’ for a while first.

Regardless, I feel compelled to conclude that the above, in general, must be considered fairly strong evidence supporting the validity of the proposed solution to the Z32 given in this thread. Indeed, for myself, I would be personally happy to leave the process of evaluation there.

You may think differently, however. Let me know if you do.

Posted by: @shaqmeister

In short, whereas there are found to be 5 common symbol encodings between the Z340 and the proposed Z13/32, 4 common symbol encodings between the Z340 and the Z408 and 5 between the Z408 and the Z13/32, there are included in these three which are evidently persistent across all the keys. And this, to my thinking, is hardly consistent with anything we might expect from chance.

To finish up this idea, it is probably worth while trying to make the attempt to quantify the chance probability according to the above findings. This would appear particularly indicated, as it cannot be merely passed over that the plaintext equivalents in question — ‘E’ and ‘I’ — are among those occurring with the highest frequency in English. We should therefore expect to be present a statistical contribution tending towards pseudo-non-randomness from the fact that each will most likely exhibit a high proportion of homophones in any competently produced cipher. Our criteria for evaluating actual non-randomness must therefore be set higher than if, say, we were considering homophones for ‘K’ and ‘Q’.

Statistical analysis is not, unfortunately, a speciality of mine. However, I will give it a try and if there are any glaring errors someone better informed than me can correct them.

To begin, then.

There are 6 symbols in the Z340 encoding the plaintext letter ‘E’ and this is out of a total of 63 unique symbols, so that the proportion of symbols in the Z340 encoding ‘E’ is 6/63 or 2/21. This, then, quantifies the probability of a symbol encoding ‘E’ in the Z408, being carried over into the Z340 again giving ‘E’ by chance. There are, however, 7 symbols in the Z408 for ‘E’ and all of these are present in the Z340 with some encoding, whilst only 4 carry through to the Z13/32. So, the probability of any one of these 4 alone being randomly carried over to give ‘E’ in the Z340 will be equal to (4 × 2)/21 ≈ 2/5.

In the proposed key for the Z13/32 we have 4 symbols encoding ‘E’, out of a total of 32, which amounts proportionately to 1/8.

Thus the combined chance probability of any one of the 4 perpetuating characters encoding ‘E’ in the Z408 achieving the same simultaneously in both the Z340 and the Z13/32 would amount to approximately 2/5 × 1/8 = 1/20.

If, then, we run through the same for one of the 3 symbols encoding ‘I’ in the Z408 perpetuating through the Z340 and on to the Z13/32 — the fourth, ‘U’, doesn’t reach the 13/32 — we find the chance probability to be close to 1/27. Likewise, for either of the remaining 2 of this set of symbols in the Z408 again doing the same, the probability comes out at approximately 1/40.

So, if we are to have all three of these combinations simultaneously, then the overall chance probability would amount to something close to:

1/20 × 1/27 × 1/40 = 1/21600

And that, as stated, does not appear trivial.

Indeed, to put it into some sort of context, it would be the equivalent of me trying to guess in advance at what point during a given six-hour period you are going to erupt with a single hiccup, and then getting it right precisely to the second.

Posted by: @shaqmeister

Thus, if you were somehow to be aware of these three pervasive repeats from the start (which is hypothetical, of course, as knowledge of their carrying through all of the ciphers would require actual solving of the last two, as here), and then if you were to merely apply the assumptions set out in the first post of this thread, then you would basically have everything you need to solve all but the range in the Z32.

But, hold on. Maybe not so hypothetical, after all. Sure, we can’t have knowledge of the three cipher symbols that we are proposing run consistently through all four ciphers with the same plaintext unless we first assume the last two ciphers to be solved. But, all the same, it is possible to suppose that we might have been given something of a similar nature to help us on our way.

Consider again the Z32 and the Z13 as we have been doing throughout, marked up with colour coding to indicate duplicates within the Z32 cipher and common symbols across the two ciphers taken together. Likewise, let’s have the plaintext marked up to reflect the assumptions that were introduced in the first post and which have been carried through also — that the blocks of plaintext marked according to the three colours here are, in the first instance, assumed to equate to the same words across the two ciphers.

Then, on the basis of these assumptions, it would appear reasonable to suppose that an attack might first be made on determining what single letter corresponds to the three 8-balls in the Z13. So, to illustrate such, equivalent cipher symbols have been set in the plaintext row of each cipher (below) to indicate which symbols from the Z32 equate to these three 8-balls in the 13.

What we find as their equivalents are: ‘P’, ‘open triangle’ and reversed-‘K’.

That might not seem much, initially. Until, that is, we glance over the key for the Z408 and find all three of these symbols present and representing the one single plaintext letter, ‘I’, which is just the very encoding we have found for each, here, in the Z13/32.

And that might just appear non-random enough (chance prob. ≈ 1/500) so that we might start out with a first trial from here, even if we are quickly disillusioned through finding that the complete Z408 key, simply applied throughout, gets us nothing further.

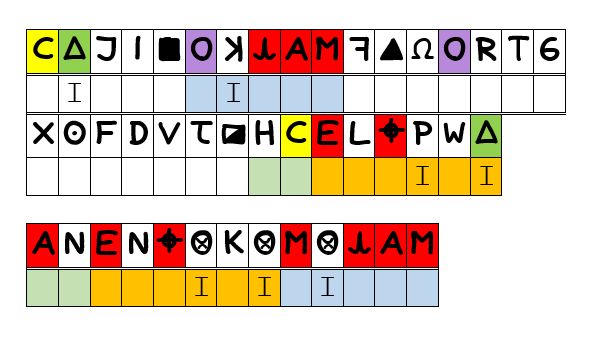
As for the trial itself, there is nothing new to add here except that now, with just this seemingly meagre beginning also assumed as intentionally given, we are able to fix — rather than just guess — the ‘EIGHT’ for the first word in plaintext, from which the whole is then all but trivially deduced. That is to say, beyond just a solution, we can now propose what would likely have been the expected steps leading to solution.

Adhering to the initial assumptions, we get the 8-balls directly from the Z408 key. Fixing the ‘EIGHT’, alone, produces the severely limiting ‘_ E _ I _ I’ for the 6-letter word (orange) at the end, which presents no plausible alternatives to ‘GEMINI’. The units, both for bearing and range, are given to us directly with the Phillips map — 30 degree units for angle (from added compass rose, blue), and inches for distance (from scale).The ‘NE’ (light green), at this point, is fully determined. Finally, as to the specific range, ‘ANDSEVENINCHES’ is off the map to the west, ‘PLUSFIVEINCHES’ falls in the sea west of San Francisco.

Control

Since the second part of the above evaluation (here), looking specifically at the proposed Z13/32 key in relation to those of the earlier Z408 and Z340, identified a number of instances of apparently non-random common threads running across all of them, it would appear useful to introduce by way of a ‘control’ an independent proposed solution to the Z32 to see how it fares under the same scrutiny. Of the commonalities noted above, the two that stood out the most comprised:

1. identification of three concurrent uses of a single ciphertext symbol in each case encoding the same plaintext letter across all three keys, occurring with an assessed probability of 1/21600, by chance; and
2. identification of a single instance of three (out of four) symbols representing the plaintext letter ‘I’ in the Z408 being carried into the Z13/32 under the same encoding, with an assessed probability of 1/500, at just those places in the Z32 which, under the assumptions set out in the first post, correspond to the three 8-balls in the Z13.

Through the following control exercise, the primary question need only be: do we necessarily see anything of the same nature, and approaching the same degree, arising for other alternative proposed solutions?

As the control example the following will be used, which is one potential solution proposed under the grandiose heading of “December 27th 2020 — The day the Z32 was solved,” which can be found online here, for those interested.

It comprises a straight and consistent fit into the Z32 alone, according to its internal constraints through the three once-duplicated symbols, as here:

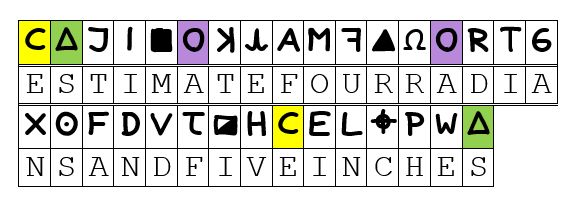
It is not the intention here to provide any comment as to the merit or otherwise of this as a valid solution, but merely to study the resultant key in the manner that was laid out above in respect of the proposed joint Z13/32 key.

Here, then, for the key in this instance we have the following:

whilst the commonalities across the three ciphers fall out as in the table below:

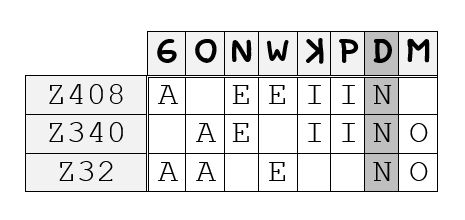
Here, as of course must be the case, there can be no instance of any given symbol encoding the same plaintext letter across just the two keys to the 32 with a probability less than 1/29 and, in fact, the actual probabilities range between about 1/10 and 1/3. There are no instances of any one of the four most common vowels — ‘A’, ‘E’, ‘I’, ‘O’ — being encoded by the same symbol in all three keys. The one instance of the cipher symbol ‘D’ encoding ‘N’ across all three keys can, as previously, be evaluated as to its chance probability as follows.

Thus, with 5 available symbols in the key for the Z340 encoding ‘N’, the probability of any one symbol from the Z408 with this encoding repeating in the 340 and, again, encoding ‘N’ will be 5/63. There are, however, 2 symbols from the Z408 encoding ‘N’ which perpetuate up to the proposed key for the Z32, and so the chance of either one or the other encoding ‘N’ in the 340 will be 10/63. In the Z32 itself, there are 3 symbols encoding ‘N’ so the chance of any symbol with the same encoding in the 340 encoding the same in the 32 will be 3/29. The combined probability over all three keys will thus be:

10/63 × 3/29 ≈ 1/63

which, again, is no less probable than that any given symbol in the Z408 key should find itself randomly achieving any encoding whatsoever in the key for the Z340. In short, what we have here is a picture of complete randomness, right across the board.

Of course, although this result of itself does not, and cannot, speak to the evident non-randomness observed in the prior proposed key (passim.) necessitating the conclusion that the same must be the correct one, it is nonetheless the case that, if not correct, then some explanation has then to be found for why its significant degree of comparative non-randomness is present.

In essence, the one overriding question — genuinely asked — would appear in my view to have been fully flipped from “Can this be right?” to “Is it possible that this could, in fact, be wrong?”

Forget about whether the solution you or Druzer proposed is correct – but ask yourself one question – can either solution be reasonably proposed before the Little List letter was even mailed. The Zodiac clearly believed that a location for the bomb could be determined through the Phillips 66 map alone, without the additional later “concerns radians & inches” clue. Therefore, any solution has to be achieved without the Little List letter.  

Posted by: @richard-grinell

The Zodiac clearly believed that a location for the bomb could be determined through the Phillips 66 map alone, without the additional later “concerns radians & inches” clue. Therefore, any solution has to be achieved without the Little List letter.  

Yes. I absolutely agree with this, as I discuss here.

Posted by: @richard-grinell

Forget about whether the solution you or Druzer proposed is correct …  

I’m just taking a closer look at the example I had included above as a control solution, and which you have attributed to @Druzer — this one:

— and I’m wondering how the actual coordinates here came to be proposed in the first place.

It is, of course, trivial to overlay on the Phillips map all viable combinations of unit angles in radians and unit distances in inches that make landfall, as below:

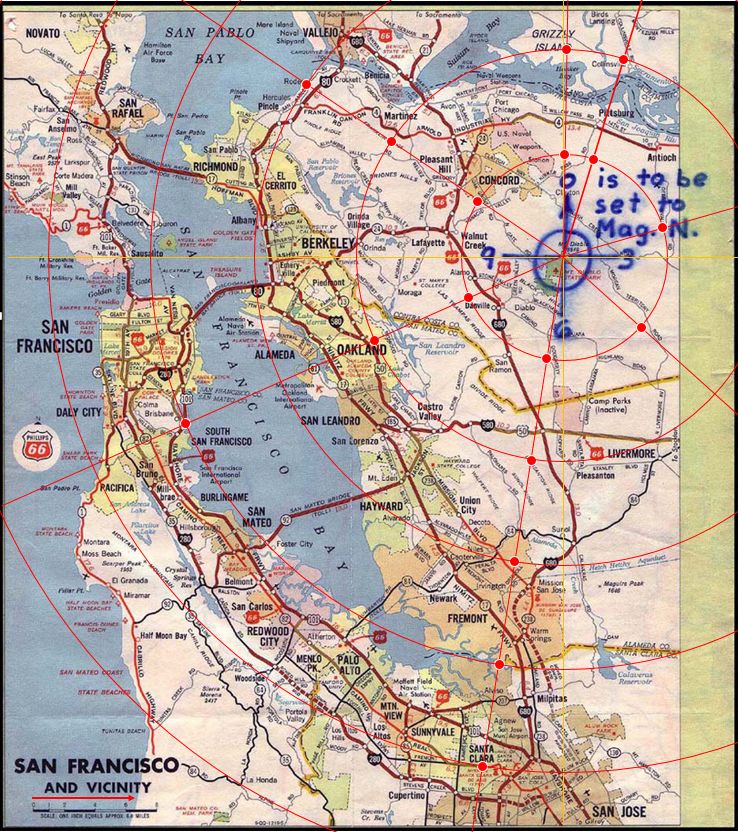
4 radians and 5 inches, however, isn’t one of them.

All I did was overlay the crosshairs with the dark circle over a compass rose, which was Zodiac’s guide to 4 radians (set to MagN) = 246.2 degrees. With SFPD next to it, this had to factor into his target. With SFPD the target, only 5 inches lands over San Francisco using the map scale. The hashtag (which represents the word “number”) before inches (with the arrow pointing here) on “P.S. The Mt. Diablo code concerns Radians + # inches along the radians”, indicates the number five should be inserted here. The statement of the “code concerns Radians & inches”, to me, indicates the code must contain the words inches and radians. Therefore, the answer is “four radians and five inches”, to be coupled with the map of Magnetic North (17 degrees). Placed in the code from characters 9 to 32, only the word ESTIMATE satisfies the first 8 characters (with 3 repeating). Ingleside PD is 251 degrees from Mount Diablo. The angle and distance of Ingleside is 97.5 % accurate. The choice of SFPD (or elsewhere) as the target was never going to land exactly on a whole number of radians and inches, so I suspect he gave us a guide or estimate. No other amount of radians or inches falls in San Francisco, and when he brought up the Park Police Station bombing and stated “it wouldn’t do to move into someone elses territory”, I suspect he chose Ingleside as an alternative. Alongside Ingleside is the Southern Freeway, matching every detail on his April 20th 1970 diagram. I’m satisfied it is the answer, but I realize others disagree (such as yourself). We all have to find the answer we believe in Shaqmeister.   

Posted by: @richard-grinell

All I did was overlay the crosshairs with the dark circle over a compass rose, which was Zodiac’s guide to 4 radians (set to MagN) = 246.2 degrees.

That would be then, I guess, the “crosshairs with the dark circle” from the Little List letter?

Confused now, as:

Posted by: @richard-grinell

The Zodiac clearly believed that a location for the bomb could be determined through the Phillips 66 map alone, without the additional later “concerns radians & inches” clue. Therefore, any solution has to be achieved without the Little List letter.

Posted by: @richard-grinell

We all have to find the answer we believe in Shaqmeister.

Just on a personal note, I’m looking to find the answer that is correct.

Unfortunately Shaq, very few in the Zodiac community can agree on even the most obvious things, like the killer sent the shirt piece, so I doubt any solution (however convincing) will satisfy many. Without the Little List letter, the bomb was to be set a certain number of degrees around the crosshairs and a set distance from it. Every threat regarding bombs had been centered around San Francisco, mailed to the San Francisco Chronicle and included SFPD=0. The map was also “San Francisco & Vicinity”, therefore it makes more sense to begin with a threat aimed at San Francisco as the starting point. Using miles, km, or feet, any number of these can fall inside San Francisco, so we have to choose a unit of measurement that only one answer can exist. Using the map scale of 6.4 miles to the inch (bearing in mind the east-west distance of San Francisco) only 5 inches, or 32 miles falls within San Francisco. Equally, the angle around the crosshairs can’t be formulated in degrees, because any number of whole degrees lands within the north-south axis of San Francisco. Therefore, it has to be an angular measurement that falls inside San Francisco where only one answer exists. That is 4 radians. Neither 1, 2, 3, 5, or 6 falls within San Francisco (with or without Magnetic North). So, without the Little List letter we can conclude Zodiac chose inches and radians. Going back to your statement of wanting the correct answer, if you or I had suggested on June 26th 1970 that Zodiac must be using radians and inches to set the bomb (and must be 4 radians and five inches), and on July 26th 1970 the Zodiac confirmed the Mt Diablo code concerned radians and inches, do you think anyone would still believe this was the answer. The answer, is of course no. The composition of the 32 symbol cipher, with 29 unique characters,  is such, that people will dismiss everything presented in absence of a viable key later given by Zodiac. How do you prove a solution correct for a 29/32 unique character construction? I can’t prove the one I’ve presented here is correct to anybody’s satisfaction. If you are satisfied that your solution is correct Shaq, does it really matter what anyone else thinks. It’s always nice when people agree with you, but it doesn’t make any difference to whether it’s true or not.

Posted by: @richard-grinell

Without the Little List letter, the bomb was to be set a certain number of degrees around the crosshairs and a set distance from it. Every threat regarding bombs had been centered around San Francisco, mailed to the San Francisco Chronicle and included SFPD=0. The map was also “San Francisco & Vicinity”, therefore it makes more sense to begin with a threat aimed at San Francisco as the starting point.

Yes on your case for San Francisco here, except for a slight clarification that I’d want to not pre-empt your subsequent point by using “a certain number of degrees around,” but instead “a certain angle.” As you yourself argue, I can’t imagine that, at this point, he would be moving back out of the city.

Posted by: @richard-grinell

Using miles, km, or feet, any number of these can fall inside San Francisco, so we have to choose a unit of measurement that only one answer can exist. Using the map scale of 6.4 miles to the inch (bearing in mind the east-west distance of San Francisco) only 5 inches, or 32 miles falls within San Francisco.

Incorrect on this one, I’m afraid, as my figure in a previous post demonstrates clearly. All I can guess is that you are maybe using the conversion scale of the very inexact Phillips map to calculate a distance in miles, then applying this distance in miles against some accurate measurement of the distance to San Francisco on, say, Google Maps?

Don’t!

The scale of the Phillips map is in inches, the code gives a distance in inches. Measure the distance on the map in lengths according to what equates to one inch against the scale. Five inches hits the sea.

Posted by: @richard-grinell

Equally, the angle around the crosshairs can’t be in degrees, because any number of whole degrees lands within the north-south axis of San Francisco. Therefore, it has to be an angular measurement that falls inside San Francisco where only one answer exists. That is 4 radians. Neither 1, 2, 3, 5, or 6 falls within San Francisco (with or without Magnetic North). So, without the Little List letter we can conclude Zodiac chose inches and radians.

On the contrary, without the Little List letter we would not be distracted beyond what we are directly given on the Phillips map, that we are to count out the angle clockwise in units of 30 degrees each.

Posted by: @richard-grinell

How do you prove a solution correct for a 29/32 unique character construction?

This is a very important question, isn’t it? Unfortunately, most times it gets asked it is posed as if it is necessarily rhetorical. I would only disagree with the ‘necessarily’ here. If the Zodiac did not intentionally incorporate any deeper constraints into the Z32 than just the three repeats, then there would be little to separate any one potential solution from another. That’s why I am setting out to test whether or not there are indeed further constraints that we can identify and validate, independently or otherwise of any specific solution.

We don’t actually know how the Zodiac calculated the distance in miles (say 31 miles to Ingleside for example). If he just used the scale and applied 5 inches, then absolutely it would fall in the sea. If however he used longitude and latitude points to calculate distance, then applied the code using the miles to achieve the inches, he can arrive at the correct distance of approximately 5 inches. It depends on how clever the Zodiac was. It’s not impossible he worked in a relevant industry supplying such skills. I go back to “P.S. The Mt. Diablo code concerns Radians + # inches along the radians”. Concerns = relate to; be about. If the code was about radians and inches, one could argue that the code has to contain both these words, irrespective of the value we think they are. We both agree inches is there. Clearly, the Zodiac Killer knew that 29 unique characters was problematic, as was the brevity of his 13-Symbol cipher, so why he chose to incorporate 29 unique characters could indicate a completely different system to standard cryptographic methods. I did try the old A=1, B=2, C=3 system to add up the total of forward facing alphabetical letters in the Z32. Curiously, it added up to 234 (degrees), coupled with the map of 17 degrees MagN = 251 degrees = Ingleside PD. Irrespective of whether this was meant (I’m not convinced), some technique using code solving rather than cipher solving, probably needs applying.