Ok…so I happened to come across an article mentioning a group called Four-Pi that was very active in murders at the time of Z. What struck me as unusual is that Z’s symbol has 4 divisions (4 pieces of a pie ![]() ). So, 4 Pi is actually the the angular measure of a complete sphere (solid angle) – 4π steradians.
). So, 4 Pi is actually the the angular measure of a complete sphere (solid angle) – 4π steradians.
A Steradian is
The steradian (symbol: sr) or squared radian is the SI unit of solid angle. It is used in three-dimensional space, and functions analogously to the manner in which the radian quantifies planar angles. The name is derived from the Greek stereos for "solid" and the Latin radius for "ray, beam".
The steradian, like the radian, is dimensionless, essentially because a solid angle is the ratio between the area subtended and the square of its distance from the vertex: both the numerator and denominator of this ratio have dimension length squared (i.e., L²/L² = Φ – no unit). It is useful, however, to distinguish between dimensionless quantities of different nature, so in practice the symbol "sr" is used to indicate a solid angle. For example, radiant intensity can be measured in watts per steradian (W·sr−1). The steradian was formerly an SI supplementary unit, but this category was abolished from the SI in 1995 and the steradian is now considered an SI derived unit.
http://en.wikipedia.org/wiki/Steradian
So I went on to check out more about steradians:
In geometry, a solid angle (symbol: Ω) is the two-dimensional angle in three-dimensional space that an object subtends at a point. It is a measure of how large the object appears to an observer looking from that point. In the International System of Units (SI), a solid angle is expressed in a dimensionless unit called a steradian (symbol: sr).
A small object nearby may subtend the same solid angle as a larger object farther away. For example, although the Moon is much smaller than the Sun, it is also much closer to Earth. Therefore, as viewed from any point on Earth, both objects have approximately the same solid angle as well as apparent size. This is evident during a solar eclipse.
http://en.wikipedia.org/wiki/Solid_angle
Now a solid angle is characterized by the "Omega" symbol as shown above….and Z used that.
I know there has been a lot of talk about Z using radians since that is what he stated in his letter, but what if he used these steradians and plotted it on the map according to the earth being a sphere, and not a flat surface as a map would show it, but rather from a globe?
And back to the 4-pi movement cult, they also collected slaves and had NUMEROUS other famous killers among their ranks. They were a fairly large cult and Manson and Berkowitz were both members. The leader of 4-Pi was called the "Grand Chingon" and was said to be a very influential and wealthy California Business man. It just really piqued my curiosity reading about the 4-Pi group in that the leader would tell others to go kill for him. So just thinking outside the box here, say Z was multiple killers with a single person that was writing the letters, such as the leader. Z would always look different and the letter writer, whom I also think was highly intelligent and misspelling for fun, could have been the highly intelligent and wealthy California business owner.
I would wonder if Mr.X was ever linked to this group.
Again…just interesting links to things that may or may not have anything to do with the case.
Oh….and the steradian thing is way over my head as far as mathematics goes, so there is no chance I could actually work this out in any way….just seemed like an interesting connection and I haven’t found anything on anyone checking into steradian angles or measurement in regards to Z.
Various writings place this mysterious businessman in L.A., not S.F. — so probably not Mr. X…
Incidentally, cannibal murderer Stanley Dean Baker, the one who came forward with the "Four Pi" story, was involved with the 1970 murder of Robert Salem, where "ZODIAC" and "SATAN SAVES" were scrawled on a wall in the victim’s blood.
http://murderpedia.org/male.B/b/baker-stanley-dean.htm
Various writings place this mysterious businessman in L.A., not S.F. — so probably not Mr. X…
Incidentally, cannibal murderer Stanley Dean Baker, the one who came forward with the "Four Pi" story, was involved with the 1970 murder of Robert Salem, where "ZODIAC" and "SATAN SAVES" were scrawled on a wall in the victim’s blood.
Yeah, I read about him and that case….pretty messed up. At the end he recanted the while 4-pi story and said he just wrote those things for shock value on the wall. I personally believe he was involved with the group….he knew too many details not to be.
As far as the Mr.X think goes, I would think the head of an organization would keep his actual living space private and hold meetings elsewhere. He was Uber rich and could have traveller to the meetings anytime.
Santiago Park isn’t that far from O’Neil Park were they had there rituals in the Santa Ana mountains. Some more here on the last post. viewtopic.php?f=99&t=1032
The trouble with any kind of cult connection – for me – is simply the nature of the known crimes. They don’t fit the idea – not even LB does that in my opinion. The only way in which they may conceivably fit, is if all the victims were involved somehow with a cult themselves – and were eliminated because they knew too much (or something along those lines). And nothing indicates they were involved with any cult, let alone the same cult.
The letters don’t fit either as I see it. To put it both vaguely and precisely at the same time, I think they’re all clearly written by the same person – or by persons who all made an effort to create that impression. Which may fit many theories – but not the cult idea. Not for my money.
Santiago Park isn’t that far from O’Neil Park were they had there rituals in the Santa Ana mountains. Some more here on the last post. viewtopic.php?f=99&t=1032
Some more possible connections here http://zodiackiller.fr.yuku.com/reply/1 … ply-145458
Hi,
The Four-Pi Movement is linked to The Process, which I have just posted on. This is very interesting!
viewtopic.php?f=96&t=2202
"As the cult grew, the DeGrimstons withdrew further from the outer world, occupying a zone of secrecy and exclusion, penetrated only by the oldest members. They called themselves The Omega (see symbol, left); apparently they had fused into a single, psychic entity. Robert, whose long hair, beard and dreamy expression made him look increasingly like Christ, could still be seen at lectures, where his charismatic voice preached the approaching conflagration. Mary Ann was rarely seen by lower ranking members; the hierarchical system of neophytes, initiates, priests and ‘Brothers’ was strictly enforced, and the secret rituals of the Omega were a matter of some speculation among new devotees."
Also, The Process produced a magazine that has artwork that resembles the art from the zodiac cards.
(dubdubdub.satanservice.org/propaganda/process.html)
(dub.dub.dub.satanicmojo.blogspot.com/2014/06/the-process-x-marvel-comics.html)
Ok…so I happened to come across an article mentioning a group called Four-Pi that was very active in murders at the time of Z. What struck me as unusual is that Z’s symbol has 4 divisions (4 pieces of a pie
). So, 4 Pi is actually the the angular measure of a complete sphere (solid angle) – 4π steradians.
A Steradian is
The steradian (symbol: sr) or squared radian is the SI unit of solid angle. It is used in three-dimensional space, and functions analogously to the manner in which the radian quantifies planar angles. The name is derived from the Greek stereos for "solid" and the Latin radius for "ray, beam".
The steradian, like the radian, is dimensionless, essentially because a solid angle is the ratio between the area subtended and the square of its distance from the vertex: both the numerator and denominator of this ratio have dimension length squared (i.e., L²/L² = Φ – no unit). It is useful, however, to distinguish between dimensionless quantities of different nature, so in practice the symbol "sr" is used to indicate a solid angle. For example, radiant intensity can be measured in watts per steradian (W·sr−1). The steradian was formerly an SI supplementary unit, but this category was abolished from the SI in 1995 and the steradian is now considered an SI derived unit.
http://en.wikipedia.org/wiki/Steradian
So I went on to check out more about steradians:
In geometry, a solid angle (symbol: Ω) is the two-dimensional angle in three-dimensional space that an object subtends at a point. It is a measure of how large the object appears to an observer looking from that point. In the International System of Units (SI), a solid angle is expressed in a dimensionless unit called a steradian (symbol: sr).
A small object nearby may subtend the same solid angle as a larger object farther away. For example, although the Moon is much smaller than the Sun, it is also much closer to Earth. Therefore, as viewed from any point on Earth, both objects have approximately the same solid angle as well as apparent size. This is evident during a solar eclipse.
http://en.wikipedia.org/wiki/Solid_angle
Now a solid angle is characterized by the "Omega" symbol as shown above….and Z used that.
I know there has been a lot of talk about Z using radians since that is what he stated in his letter, but what if he used these steradians and plotted it on the map according to the earth being a sphere, and not a flat surface as a map would show it, but rather from a globe?
And back to the 4-pi movement cult, they also collected slaves and had NUMEROUS other famous killers among their ranks. They were a fairly large cult and Manson and Berkowitz were both members. The leader of 4-Pi was called the "Grand Chingon" and was said to be a very influential and wealthy California Business man. It just really piqued my curiosity reading about the 4-Pi group in that the leader would tell others to go kill for him. So just thinking outside the box here, say Z was multiple killers with a single person that was writing the letters, such as the leader. Z would always look different and the letter writer, whom I also think was highly intelligent and misspelling for fun, could have been the highly intelligent and wealthy California business owner.
I would wonder if Mr.X was ever linked to this group.
Again…just interesting links to things that may or may not have anything to do with the case.
I know there has been a lot of talk about Z using radians since that is what he stated in his letter, but what if he used these steradians and plotted it on the map according to the earth being a sphere, and not a flat surface as a map would show it, but rather from a globe?
OMG!!!! You just described boundary functions.
https://answers.yahoo.com/question/inde … 949AAx9pbQ
"I was doing a report on the unibomber off google and saw his math phd dissertation and was wondering if this stuff actually makes sense to anyone and if so, What exactly is it talking about in more "understandable math terms".
Let H denote the set of all points in the Euclidean plane having positive y-coordinate, and let X denote the x-axis. If p is a point of X, then by an arc at p we mean a simple arc v, having one endpoint at p, such that v – {p} ( H. Let f be a function mapping H into the Riemann sphere. By a boundary function for f we mean a function t defined on a set E ( X such that for each p ( E there exists an arc v at p for which
lim f(z) = t(p).
z -> p
z ( v
The set of curvilinear convergence of f is the largest set on which a boundary function for f can be defined; in other words, it is the set of all points p ( X such that there exists an arc at p along which f approaches a limit. A theorem of J.E. McMillan states that if f is a continuous function mapping H into the Riemann sphere, then the set of curvilinear convergence of F is of type F(sd). In the first of two chapters of this dissertation we give a more direct proof of this result than McMillan’s, and we prove, conversely, that if A is a set of type F(sd) in X, then there exists a bounded continuous complex-valued function in H having A as its set of curvilinear convergence. Next, we prove that a boundary function for a continuous function can always be made into a function of Baire class 1 by changing its values on a countable set of points. Conversely, we show that if t is a function mapping a set E ( X into the Riemann sphere, and if t can be made into a function of Baire class 1 by changing its values on a countable set, then there exists a continuous function in H having t as a boundary function. (This is a slight generalization of a theorem of Bagemihl and Piranian.) In the second chapter we prove that a boundary function for a function of Baire class e > 1 in H is of Baire class at most e + 1. It follows from this that a boundary function for a Borel-measurable function is always Borel-measurable, but we show that a boundary function for a Lebesgue-measurable function need not be Lebesgue-measurable. The dissertation concludes with a list of problems remaining to be solved.
Best AnswerAsker’s Choice
Cool Dude answered 6 years ago
This is very coherent if you know the terms he’s using. The only insight I can glean from this abstract is that he was a pretty typical mathematician.
To explain what he’s doing, first consider a continuous function f(x) from the open interval (0,1) to the real number line. You might ask, "Can I extend this to a continuous function on the closed interval [0,1]?" In other words, you’re trying to extend the function to its boundary points, 0 and 1. If the limit of f(x) as x goes to 0 exists, then you can reasonably define f(0) to be this limit; similarly for f(1). But if one of these limits doesn’t exist, you can’t extend f(x) to a continuous function at that point. What are all of the possibilities? Four: we can extend f(x) to a function on [0,1], (0,1], [0,1), or (0,1). And we can realize all of these perfectly well with the functions f(x) = x, f(x) = 1/x, f(x) = 1/(1-x), and f(x) = 1/(x^2-x), respectively.
Now what is the Unabomber doing? Instead of his functions taking values from the interval (0,1), it takes values from an upper half plane, i.e. the points lying above the x-axis in the plane, or equivalently the points (x,y), with y > 0 and x arbitrary. This set has a boundary like (0,1) does, a set of points that separate it from the rest of the plane–the x-axis, the set of points with y = 0. And instead of the range of the function being in the real numbers, it’s in the surface of a sphere (here realized as the Riemann sphere, which is the complex plane plus a "point at infinity").
So he’s asking: given a continuous function f(x) from the half plane to the sphere, what can I say about extending this to a continuous function on the boundary, i.e. the x-axis? First, what does he mean by continuous here? There are a lot of different directions that I can approach the x-axis from the half plane–perpendicularly, at an angle, on a spiraling trajectory, etc. The Unabomber says he doesn’t care what sort of path you take to get to the boundary, just so long as ONE exists so that the limit of f(x) "along this path" exists. And then we can define f(x) at this boundary point as this limit.
Next, how many possibilities can there be? I.e., given a function, what subset of points of the boundary can you extend the function to? In the previous case of the interval and the real line, the boundary only had two points, so I only had to worry about a finite number of possibilities. The x-axis is a line. It contains infinitely many points. So there are infinitely many subsets. So the possible sets of boundary points to which you can extend a continuous function is potentially huge. In fact, the Unabomber shows this to be true. However, continuous functions are pretty special, so the sorts of sets you can get above shouldn’t be too ugly. And, indeed, he shows this.
Asker’s rating & comment
5 out of 5
very impressive understanding of abstract mathematics
Very interesting! Yes Ted K did his thesis on boundary functions IIRC.
I don’t really understand it much but as you note it is a subset of math and geometry. It is very complex and abstract a lot of it deals with circles and spheres.
MODERATOR
Deeper and deeper the rabbit hole goes.
Darla….I have absolutely NO idea what I am reading in your post. I studied a LOT of math in college, but have used none of it since.
Does what you posted lend more credibility to a TK/Z link?
I am wondering if anyone that knows more about steradians can check on the Z map with steradians in mind, rather than just radians.
Would be really cool to me if someone could uncover the bomb, if there was one, based on using this method and actually being able to pinpoint the device.
I am getting my own interest "re-piqued" in this possibility again. So, the "Omega" symbol that Z used and stated in his letter that the code coupled with the map would allow the bomb to be found…..could the Omega symbol be part of a steradian geographical coordinate? The coordinates being the code and the Omega symbol being used in the correct place to signify steradians?
Reading about celestial coordinates along with steradians, and again I am way out of my league here, it would seem that the number of characters in the code pre and post omega symbol, could match up with coordinate systems…..celestial, equatorial, etc, or a mix of both with the Omega symbol being used as a "pivot" of sorts, denoting steradians are in use?
Hi, I think if we look at these clues with these connections in mind, we might be able to figure out where the bomb is.
The most important part of the information I posted is in the middle of this explanation of TJK’s thesis on boundary functions. The first guy asks, "what does this all mean?" and the second guy responds with an excellent answer which ties into your idea of 4 pie. Which also ties into my idea of the Omega, which is English couple Mary Anne and Robert DeGrimston;originally Robert Moor and Mary Anne MacLean).
What TJK did was find an easier way to find the points on a circle by going into three dimensional space and figure it out from there. This is what you pointed out with the idea of the solid angle ( which is characterized by the "Omega").
Now what is the Unabomber doing? Instead of his functions taking values from the interval (0,1), it takes values from an upper half plane, i.e. the points lying above the x-axis in the plane, or equivalently the points (x,y), with y > 0 and x arbitrary. This set has a boundary like (0,1) does, a set of points that separate it from the rest of the plane–the x-axis, the set of points with y = 0. And instead of the range of the function being in the real numbers, it’s in the surface of a sphere (here realized as the Riemann sphere, which is the complex plane plus a "point at infinity").
So he’s asking: given a continuous function f(x) from the half plane to the sphere, what can I say about extending this to a continuous function on the boundary, i.e. the x-axis? First, what does he mean by continuous here? There are a lot of different directions that I can approach the x-axis from the half plane–perpendicularly, at an angle, on a spiraling trajectory, etc. The Unabomber says he doesn’t care what sort of path you take to get to the boundary, just so long as ONE exists so that the limit of f(x) "along this path" exists. And then we can define f(x) at this boundary point as this limit.
http://www.californiarealestatecourses. … es12_8.htm
http://www.californiarealestatecourses. … es12_7.htm
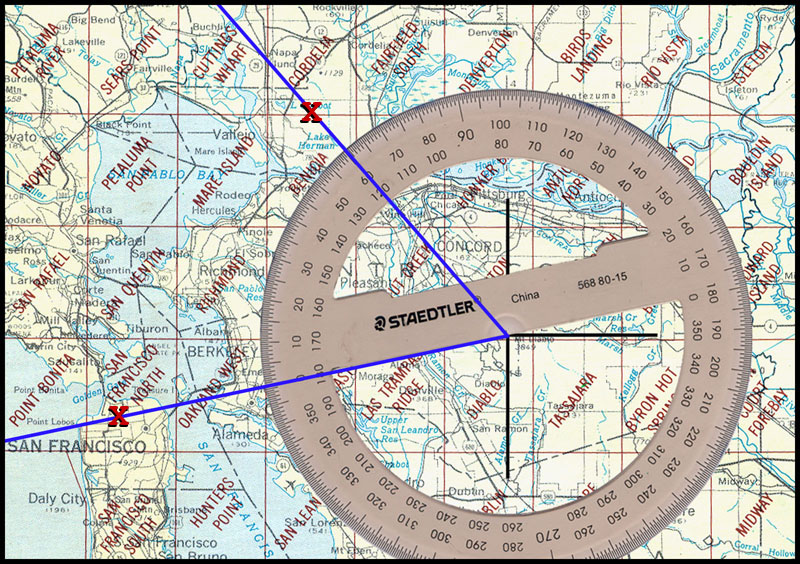
IMO, The first clue to this map is the fact that Z uses the Mr. Diablo meridian as a starting point. This means that the answer to the coded message is going to be limited to a certain number of letters.
The three intersections in California are the Humboldt, Mt. Diablo and San Bernardino (HBM, MDBM, SBBM).
Any specific township square is identified by stating the township number, the range number and the name of the principal meridian and base line. Thus, we might have a description which reads: Township 3 North, Range 4 East, San Bernardino Base and Meridian (T3N, R4E, SBBM).
N,S,E,W,R,H,B,M,D,S,T
The omega is in this clue and has never been used before. So, maybe, somehow it’s significant. The last letters could be MDBM because the bomb was buried in the bay area.
Deeper and deeper the rabbit hole goes.
Darla….I have absolutely NO idea what I am reading in your post. I studied a LOT of math in college, but have used none of it since.
Does what you posted lend more credibility to a TK/Z link?
I am wondering if anyone that knows more about steradians can check on the Z map with steradians in mind, rather than just radians.
Would be really cool to me if someone could uncover the bomb, if there was one, based on using this method and actually being able to pinpoint the device.
Z says explicitly that his puzzle has something to do with radians and inches along the radians. Why would he say that if the actual clew has to do with steradians?
The way I figure, both the following scenarios make (some) sense:
A) He actually buried something, possibly some sort of bomb, somewhere and provided his readers with real clews which would, in fact, lead to the location he had in mind.
B) He was just messing with the cops.
What does not make sense to me is this:
C) He says that his puzzle has to do with radians – but this is not the case. It actually has to do with steradians. There is a device (or whatever) buried somewhere and you can find it, but not by following the instructions he provided. You have to divine that he actually meant something other than what he said.
Z says explicitly that his puzzle has something to do with radians and inches along the radians. Why would he say that if the actual clew has to do with steradians?
The way I figure, both the following scenarios make (some) sense:
A) He actually buried something, possibly some sort of bomb, somewhere and provided his readers with real clews which would, in fact, lead to the location he had in mind.
B) He was just messing with the cops.
What does not make sense to me is this:
C) He says that his puzzle has to do with radians – but this is not the case. It actually has to do with steradians. There is a device (or whatever) buried somewhere and you can find it, but not by following the instructions he provided. You have to divine that he actually meant something other than what he said.
Steradians are also called "square radians"
Steradians are a measure of the angular ‘area’ subtended by a two dimensional surface about the origin in three dimensional space, just as a radian is a measure of the angle subtended by a one dimensional line about the origin in two dimensional (plane) space. Steradians are equivalently referred to as ‘square radians.’
So, they are radians. With all of the codes and "trickery" Z used in his writings, why WOULD he directly point us to radians and not have it actually be square radians or steradians?