good work mr wilks. it opens up the possibility of the simple answer being that he created a cipher which, when properly decoded, reveals a message hidden in within lines of garbage text. that would make a lot of sense to me as i’ve never believed zodiac was an expert cryptologist. if you wanted to make an encryption harder to crack, a la the progression from the 408 to the 340, having your statement mixed up with garbage text would certainly do so without requiring you to acquire additional encryption skills.

i realize this opens up even more implausible solutions but i think we’re on the right track and personally maintain that the solution to the 340, much like the 408, will make perfect sense once it’s revealed.

good work mr wilks. it opens up the possibility of the simple answer being that he created a cipher which, when properly decoded, reveals a message hidden in within lines of garbage text. that would make a lot of sense to me as i’ve never believed zodiac was an expert cryptologist. if you wanted to make an encryption harder to crack, a la the progression from the 408 to the 340, having your statement mixed up with garbage text would certainly do so without requiring you to acquire additional encryption skills.

i realize this opens up even more implausible solutions but i think we’re on the right track and personally maintain that the solution to the 340, much like the 408, will make perfect sense once it’s revealed.

Thanks!

I think the first stage solution to the 340 would likely have several lines of clear English, like perhaps SEEANAME and THESEFOOLSHALL SEE and maybe HELLTOO. Several other lines may seem to be mostly or all garbled garbage, perhaps intentionally to increase difficulty of solution as you suggest, but perhaps those seeming garbage lines require a second stage solution of Cesar or something else.

Using the excellent analysis by Quicktrader showing the ++ very likely solves as LL, and from Glurk and the FBI files that normal F and normal B possibly solves as L, this is what we get:

Building from that, as Graysmith also solves + , F, and B all as L, I then add in strong logical possible word solves from the Raw Graysmith of SEE A NAME and THESE FOOLSHALL SEE this is what we get:
Note: I did not intentionally create the possible 1st line THE or the 2nd line HELLTOO. Those were created by applying the QT solves, the Glurk/FBI solves and the RG word solves of SEEANAME and THESEFOOLSHALLSEE.

After six months, finally another update:

PhD Donald Burleson has written a brilliant abstract regarding vowel-consonant-analysis.
http://www.blackmesapress.com/Crypto.htm

The main idea behind his abstract is to not only look for the contact frequencies of each symbol but to also check the contact frequencies of each adjacent symbol of those ‘root’ symbols, too.

It should be mentioned that his theory is based on Russian development, however has fairly improved the identification process. Also, due to his division with the frequency of each root symbol, it should work with homophone ciphers quite well, too.

The basic idea is to divide the contact values of each adjacent symbol by the frequency of the root symbol, therefore achieving a ‘MACC’ value while the contact values of each root symbol (the symbol analyzed) is divided by its frequency, too (called ‘VCC’). I had known about the VCC approach regarding the root symbol, even developing it further ‘through the cipher’, however not thought about analyzing its adjacent symbols. So the MACC is a good, at least complementary approach to analyze symbols with regard to their vowel/consonant status.

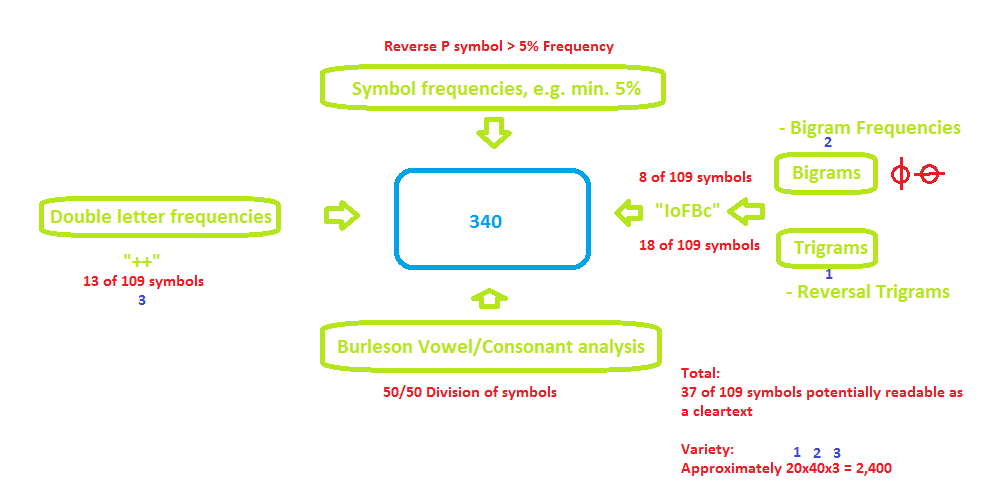
I did the Burleson-Analysis on parts of the 340. For this reason I had selected some groups of symbols of length approximately L=8 to reduce the overall cipher complexity (less cipher, less symbols). I took such groups that appear to be connected, sort of tied to each other by using as many similar symbols as possible. This allows counterchecking the groups to each other, therefore eliminating errors in cleartext or vowel-consonant analysis.

The results of the Burleson-Analysis were astonishing: Most of the symbols had a MACC value of either less than 9 or more than 11. This meaning that there is only a small group of symbols which identity (vowel or consonant) could not cleary be identified. Those symbols are potentially good ‘binders’ such as the letters ‘D’, ‘T’ or ‘N’, while symbols with a MACC value of less than 9 are potential vowels (including the two best binders ‘L’ and ‘R’) and, further, symbols with a MACC value of greater than 11 being consonants.

Identification of symbols being vowels/consonants thus got possible very clearly.

Additionally to that, the MACC values appear to be close to Burleson’s experience regarding the MACC value, e.g. 9.8 for the letter ‘N’. Based on this analysis, a symbol can be associated to a group of cleartext letters, such as ‘D’, ‘T’ or ‘N’, instead of requiring a 24 letter alphabet as being potentially correct (8 symbols usually quote with 24^8 varieties..now being e.g. 3^8 varieties, which is of course dramatically less, therefore easier to solve).

One letter showed to be distinctively a super-consonant: The letter ‘Y’ has a low MACC value of 4.5, exactly such value was found in the group I had selected, too. Looking closer to this specific symbol, it indeed had followed a double symbol. Both, the identical MACC value plus the low VCC value of the root symbol itself plus the connection to a double symbol leads me to the conclusion that this specific symbol is actually representing the cleartext letter ‘Y’. In the selected groups this symbol appears only twice, so I would not exclude the letter ‘I’ to be an alternative, however the MACC value of approx. 4.5 is in fact compliant and is a ‘Y’ following two double letters linguistically quite ok, too.

Will add some more analysis on the cipher, trying to associate various cleartext letters to symbols according to their MACC value, hopefully getting a readable cleartext in the near future.

The selected groups..the first four letters cover approx. 30% of this cipher selection.

MACC values with 3 having a 4.5, similar to Burleson’s abstract (letter ‘Y’)

QT

qt – is it possible, using this method, to decode the initial substitution part of the cipher if we assume he additionally used some other method? in other words, if he did scramble words or purposely make spelling mistakes does this method fall apart because it’s initial assumption is that certain letters appear near certain other letters or in groups?

in either case this is fascinating and potentially a very lucrative avenue for figuring out what he did. if we use this method to make determinations about what a decrypted substitution cipher 340 should look like then i assume it’d be pretty apparent, given enough time for the variants, to say with some level of certainty that he did or didn’t use this method.

Burleson must be totally blind to the color red.

Wow.

It’s like tripping on LSD.

Great work. Really interesting.

I think you made a mistake in this sentence:

"
The results of the Burleson-Analysis were astonishing: Most of the symbols had a MACC value of either less than 9 or more than 11. This meaning that there is only a small group of symbols which identity (vowel or consonant) could not cleary be identified. Those symbols are potentially good ‘binders’ such as the letters ‘D’, ‘T’ or ‘N’, while symbols with a MACC value of less than 9 are potential vowels (including the two best binders ‘L’ and ‘R’) and, further, symbols with a MACC value of greater than 11 being consonants."

AK: You say less than 9 are potential vowels but the give examples of L and R.

Can you clarify what (vowels or consonants) are typically less than 9 and what are typically higher than 11?

Hey Quicktrader,

Looking forward to what the Burleson thing might reveal for the 340.

Some ideas that I have for you is to test it on the 408 first and if possible (enough material?) to correlate for the 340 the first 10 rows versus the last 10 rows.

I’ve tried to determine a consonant/vowel map for the 340 some time ago by letting my solver make a change (+1 or -1) to an array constituting a consonant/vowel map for results that scored above a specific threshold. This worked very well for almost anything expect the 340.

And regarding contact analysis I wrote something that for each symbol compares the distance of other symbols before and after. The idea here is that in english you may have a (fictive) bigram "im" which occurs frequently but for instance "mi" occurs rarely. The measurement is so that it can differentiate between a plaintext containing english text and a plaintext that is randomized. Because in a randomized plaintext (if large enough) the bigram "im" should be equally frequent to "mi". Interestingly enough the 340 scores most random of all ciphers I have tested this way.

qt – is it possible, using this method, to decode the initial substitution part of the cipher if we assume he additionally used some other method? in other words, if he did scramble words or purposely make spelling mistakes does this method fall apart because it’s initial assumption is that certain letters appear near certain other letters or in groups?

in either case this is fascinating and potentially a very lucrative avenue for figuring out what he did. if we use this method to make determinations about what a decrypted substitution cipher 340 should look like then i assume it’d be pretty apparent, given enough time for the variants, to say with some level of certainty that he did or didn’t use this method.

Even if Z scrambled words or had typing errors, the method may lead to a solution. Currently I add additional approaches such as Trigrams..

QT

Great work. Really interesting.

I think you made a mistake in this sentence:

"
The results of the Burleson-Analysis were astonishing: Most of the symbols had a MACC value of either less than 9 or more than 11. This meaning that there is only a small group of symbols which identity (vowel or consonant) could not cleary be identified. Those symbols are potentially good ‘binders’ such as the letters ‘D’, ‘T’ or ‘N’, while symbols with a MACC value of less than 9 are potential vowels (including the two best binders ‘L’ and ‘R’) and, further, symbols with a MACC value of greater than 11 being consonants."

AK: You say less than 9 are potential vowels but the give examples of L and R.

Can you clarify what (vowels or consonants) are typically less than 9 and what are typically higher than 11?

According to Burleson the expected MACC values – in his example – are as follows:

Letter / MACC expect.
Y 4,500
E 6,385
O 6,417
A 7,000
U 7,000
I 7,500
H 8,167
L 8,500
R 8,833
G 8,857
S 8,875
F 9,000
M 9,250
B 9,250
D 9,571
N 9,800
T 10,167
C 10,333
P 12,500

However this data is not based on a large amount of text but on his example (largely based data has not yet been published, as far as I know). Nevertheless it sort of gives some indication.

QT

All above considered to solve the selected groups from the 340.

QT

Here you go with a small tool..the blue line is to enter letters. Those in a frame are bigrams or a doubletrigram. The four first blue letters will represent the most represented symbols in the selected cipher parts. Adding more than

– 5 doubletrigram plus
– 1 bigram plus
– 1 ‘++’ letters

will increase the variety dramatically. Adding additional 3-4 letters should be ok, adding more may lead to a chaos..

While a tool with 64 symbols will lead to 100 billion years of guessing, this tool rather appears to be like the TV show ‘wheel of fortune’….good luck (btw it’s the teacher approach rather than the scientific sequence analysis approach..).

QT

Excel..

Let’s assume to set a 5-gram to the cipher, e.g. on the ‘IoFBc’ position. Further, that additional letters are simply tried out one by one. All of the previous with the goal to receive a chain of (constructed) cleartext letters of at least length=8 or higher. You may then receive a looong list of such combinations with possibly only one being correct. To find out which one this could be, you may compare this list with a dictionary. This, however, still may lead to a large amount of potential results. A question that remains is if there existed any cleartext letters containing at least two words out of the dictionary (possibly leading to a correct solution, a so-called crib).

To select two words out of a cell at the same time is not so easy, especially if all of the dictionary entries shall be checked. I had quite some work with finding such solution so Excel would do that, here is the result:

=IFERROR(IF(AGGREGATE(15;6;ROW(DICTIONARY[DICTIONARY])/
(FIND(DICTIONARY[DICTIONARY];Tabelle1!C3&" ")>=1);1)=AGGREGATE(14;6;(ROW(DICTIONARY[DICTIONARY]))/
(FIND(DICTIONARY[DICTIONARY];Tabelle1!C3&" ")>=1);1);1;CONCATENATE(AGGREGATE(15;6;ROW(DICTIONARY[DICTIONARY])/
(FIND(DICTIONARY[DICTIONARY];Tabelle1!C3&" ")>=1);1);" ";AGGREGATE(14;6;(ROW(DICTIONARY[DICTIONARY]))/
(FIND(DICTIONARY[DICTIONARY];Tabelle1!C3&" ")>=1);1)));1)

with ‘DICTIONARY’ being an ‘intelligent table’ and C3 the first cell to be checked. The formula lists either two line numbers of the dictionary, e.g. 123 4008 for the two words found in a cell – or a control value (1). Íf only one word is found, it also delivers you a control value. It’s quite useful as you can now find letter combinations containing at least two words from the dictionary you have chosen, so I thought I’d share it. The idea behind is to find – under certain given criteria, e.g. the 5-gram, a phrase that contains at least two cleartext words (of course it does not work if e.g. we deal with a 10-letter word in that phrase).

QT

Hi,

I now have completed my approach to crack the 340 by focussing on line 17 of the cipher, starting with the ‘C’ symbol. I call it the FCCP-method. The method does work, however it is very computational, which still is a challenge. Nevertheless, the 340 is definitely crackable, imo:

1. Define the ‘+’ symbol (e.g. as ‘L’ – according to Bernoulli formula it has a 79% chance, second is ‘S’ with about 2.5% only)

2. Define the ‘L’ symbol according to step one. In our case (+ being an ‘L’), this is AEIOU and few other consonants (e.g. ‘w’ as in ‘owl’). Please note that the ‘L’ symbol is one previous to the ++ symbol.

3. Define the 5-gram ‘IoFBc’. It consists out of two repeating trigrams, ‘IoF’ and ‘FBc’. Both appear twice, it is likely that some other cleartext trigrams behind these cipher trigrams are actually present but well hidden behind other homophones. At least they are frequent, e.g. had a 0.5% chance to show up in the 340 twice. Both of them to be combined delivers us a 5-gram. From all 5-grams consisting of two frequent trigrams, we work us down according to a reliable frequency list 5-grams. One may soon see that only approximately 10-50 of such 5-grams actually come into focus, so we can handle them one after another. ‘QUFBZ’, for example, is not really a good candidate.

4. Define the ‘C’ symbol as being any letter from A-Z. This leads us to the i]column of our future data table.

5. Define the ‘W’ symbol and the ‘o with horizontal line’ symbol in combination as AA, AB,…ZY,ZZ (line of our table). Some combinations may be eliminated (e.g. QQ) as these two symbols follow directly after the ++ double symbol. This leads us to the line of our data table. Our data table should now have approximately 37,180 entries.

6. Set variable #1, the ‘reverse L’ symbol. Set variable #2, the ‘Zodiac symbol’. Both variables shall be checked out on each run individually, both A-Z, thus 676 settings to be done on each run.

7. Concatenate all of the above to text strings. We do get a table of so-called fictitiously created cleartext phrases (FCCPs, my term). These FCCPs may linguistically be nonsense – or not. All do have the same structure X_XXXXXXXXXXXXXXXX meaning that we do get a string of 16 letters (!) in a row. I never had imagined to even get 12..

8. Analyse the data by comparing all FCCPs with a dictionary (excel ‘aggregate’ function..please don’t ask me how..), doing so by e.g. searching for any word of length >6 or e.g. any combination of at least three words.

I did program this FCCP method by using Excel. So what was the result?

Based on the assumption that + is an ‘L’ (or whatever letter you think it should be), the creation of a table containing these 37,180 FCCPs (per run) goes like this:

a.) Entering ‘IoFBc’, e.g. ‘TIONS’
b.) Setting variable #1, e.g. as ‘C’ (RUN 2) or ‘D’ (RUN 1)
c.) Setting variable #2, e.g. as ‘B’
d.) Analyze all FCCPs from the data table with regard to linguistic structures (e.g. finding a word with length >6)

Based on the 5-gram ‘TIONS’ the results of the first two settings were the following:

RUN 1 (L, TIONS, D, B, length >6):
no result

RUN 2 (L, TIONS, C, B, length >6):
CONTROL, CENTRAL

The FCCP method does work as long as Z had used any word of length >6 in this particular 16-letter phrase (the dictionary is therefore reduced, too, as all the shorter words can be ignored, btw). The cracking process eliminates all FCCPs not containing any of such word or linguistic structure. All ‘positive’ FCCPs are shown in e.g. a structure like this:

X_XXCONTROLXXXXXXX

All of the positive FCCPs can be checked out further: Finding a second word in the phrase or looking for a logical sense by reading the results. Expansion to a string of 18-letters is possible. Wouldn’t there be any match, all words of length >5 must be searched for. However there are results:

While RUN 1 showed up with no results at all, in RUN 2 I could receive a total of 56 matches out of 37,180 (26 for each, CONTROL and CENTRAL). The procedure has thus eliminated 31,724 or 99.85% of ‘nonsense’ FCCPs. This, in fact, is the cracking process itself.

It is then possible to perform one run after another with 676 settings of variables for each 5-gram, e.g. TIONS, ATIVE,… etc. All that based on + being an L. So far the results have not led to a fully readable text. But so far I have only performed 5 runs of approximately a few thousands that are required to find the cleartext solution.

On my PC with 19 GFlops, which is quite slow, each run takes about 2 minutes. This leads us to 676 settings x 50 potential 5-grams x 2 minutes or a total of 33,800 runs x 2minutes. Thus approximately 7 weeks of calculation time is needed to check out all relevant settings (non-outlier). This is months if not years of work if we do consider changing the variables and extracting the results as well.

BUT:
If the cipher is a homophonic substitution cipher, like the 408 is, it then can be solved by using this method.

The only challenge is the computation: A computer with at least 10 Terraflops, better 100 Terraflops is required to find the cleartext solution in a reasonable time. The solution may appear on the next run or on the last..I do expect it to be found in the first third, thus 10,000 runs (with 676 settings each). Please note that the computational effort is also higher than in trial-and-error methods of sequences as the string has to be first concatenated and then checked against the complete dictionary (latter I keep small..better to apply on Z’s language and faster).

The 340 is definitely not crackproof. Anybody got a Cray computer at home?

Below you see my table starting in C10, above is an auxiliary table plus the setting of variables. It goes down to C139 and is mostly hidden (~600 columns). On the right is the dictionary plus the results found. All FCCPs containing results can be looked up by the search function (or automatically, but I keep the file simple – it has approx. 500kb only – full of complicated formulas such as the ‘aggregate’ function making it able to compare all FCCPs with all words of the dictionary):

After five runs only, I was able to rule out 5 x 37,180 = 185,900 FCCPs of promising settings in a few minutes only. So these settings have never to be tried out again (min length >6). Looking into the billions of FCCPs possible, this is still quite a fast way to eliminate all of the nonsense FCCPs. In combination with our understanding of trigram, 5-gram frequencies, the method should well deliver the result when used with appropriate computation.

Advantages of the FCCP method:
1. If Z had interrupted the sequences (e.g. ‘W’ is frequent in line 17/18, however not present in other areas of the cipher), this method still works.
2. Sequence analysis has to check-out all combinations. There is no reduction e.g. by considering a vowel (or consonant) previous to ++
3. Frequencies of trigrams, 5-grams can be considered thus the chances of finding the solution are extremely improved
4. Running a sequence analysis does not eliminate varieties. Thus on each run the same sequences could appear. The FCCP-method strictly rules out ‘wrong’ settings.
5. A direct analysis of individually defined linguistic criteria is possible. Positive FCCPs always represent a partial or fully readable text, not only a score value.
6. Intermediary peaks (hills climb..) can be avoided by further analysis of positive FCCPs while the sequence analysis usually gets stuck (or runs for ages)
7. ABCCA and vowel/consonant structures can be considered, e.g. by pre-selection in the dictionary
8. A smaller dictionary is required by e.g. searching only for words >6, which are likely to appear in a 16 or 18 letter phrase.
9. In fact it’s the fastest way to determine a cleartext solution as all of the above supports the solving process to be quicker than a simple trial-and-error method (hills climb).
10. The method is applicable on all homophone substitutionn ciphers as long as they support structures to create FCCPs of a certain length (all others are unsolvable if not all varietes are checked).

I’m gonna make this my phdoc thesis .

QT

Quicktrader,

Respect for your awesome job on this one. I think your approach could lead up to a possible solution. Keep up the good work!

Greetz,
Eduard (from the Netherlands)

I also highly respect this approach. It is very complex for an amateur like me, and even with the difficulties i have in English, but I understand with time.
The letter C as a "joker", (get this straight).
Disposal by trial and error is like a "Darwinian" analysis.
Congratulations Mr Quicktrader

Marcelo Leandro