Glad to see you guys working hard on this,let’s hope 2016 sees the 340 crumble

UPDATE:

Programming the FCCP method (doing so with ‘Python’).

Potential cleartext strings (FCCPs) shall be created under consideration of specific assumptions (e.g. the + symbol representing the letter ‘L’ and the IoFBc-quintgram being ‘THERE’). Later, the created FCCP-strings shall all be searched for individually defined linguistic criteria, e.g. words with a length >6.

Since today my very simple program actually works (so far) so that I am able to create strings consisting of e.g. the following structure in the 340-cipher:

C<+FlwBIoL++owC

In a first run, I had set-up a maximum of 600,000 strings (FCCPs). Finding one specific word in those 600,000 FCCP-strings took about 8 seconds. Thus, to check out the most likely 1,000,000,000 variants would take approximately 3.7 hours. Based on + representing the letter ‘L’ and considering the 50 most frequent quintgrams for ‘IoFBc’, we calculate:

50 frequent quintgrams
5 variable homophones (A-Z): C, <, l, w, o
1 variable homophone (AEIOU): L

is thus equal to 50 x 26^5 x 5 = 2,970,344,000 FCCP-strings

To check out all those strings would take approximately eleven hours of computation. However, we still don’t know which word we are actually looking for. We even don’t know if the string contains a word of length >6 at all. IF there is one, however, it will show up. To check out the most frequent 2,000 words with length >6 therefore leads us to

5,940,688,000,000 specific, pre-selected FCCP-strings

leading us to 916 days of computation or – using a lousy 100 Terraflop computer – 4 hours and 10 minutes.

As a result we’d receive a list of all FCCP-strings potentially containing a word of Length >6. To find a complete cleartext phrase would then require an additional (or extended) run with extra criteria, e.g. finding a second word. However this run would only take a few seconds, if at all. If the such clartext phrase is among the first 600,000 variants, it’ll show after 8 seconds only.

QT

Btw, to speed up computation the Aho-Corasick algorithm give us some support..

https://en.wikipedia.org/wiki/Aho%E2%80 … _algorithm

Let’s have a closer look at the following phrase of the 340-cipher (line 9):

ASSUMING the + symbol representing the letter ‘L’:

M+ is repeating 3 times in the cipher, thus it most likely should represent the digraph ‘AL’.
( http://www.math.cornell.edu/~mec/2003-2 … raphs.html)
( http://practicalcryptography.com/crypta … equencies/).

Now we can think about where words are actually starting and ending around this part of the phrase. Let’s have a look on the separation of words:

A separation like this

AL. L….

would lead to either ‘MALT’, ‘SALT’, ‘OVERSALT’, ‘STRINGHALT’, ‘DEALT’, ‘EXALT’, ‘HALT’, ‘BASALT’, ‘COBALT’ or ‘ASPHALT’ as a cleartext – followed by a word starting with a ‘L’. A separation of words like this:

A L.L….

would lead to either ‘LALL’, ‘LILL’, ‘LILT’, ‘LILACS’, ‘LILTED’, ‘LOLL’, ‘LULL’, ‘LOLLIPOP’, or a ‘LILLIPUT’. A text structure like this:

AL .L….

would lead to phrases such as ‘PARTIAL ILLEGITIMATE’ or comparable. And finally a text structure like this

AL.L_….

would actually lead to no solutions at all. If we assume the complete structure (‘AL.L’) to be part of only one cleartext word , such cleartext words would be limited to a few ones, too, such as ‘SALTLIKE’, ‘CALMLY’, ‘BALDLY’, ‘HALFLIVES’, ‘SCALELIKE’, ‘STALKLESS’.

This should lead us to the conclusion that Z had either used one of the following words:

‘MALT’, ‘SALT’, ‘OVERSALT’, ‘STRINGHALT’, ‘DEALT’, ‘EXALT’, ‘HALT’, ‘BASALT’, ‘COBALT’, ‘ASPHALT’, ‘LALL’, ‘LILL’, ‘LILT’, ‘LILACS’, ‘LILTED’, ‘LOLL’, ‘LULL’, ‘LOLLIPOP’, ‘LILLIPUT’, ‘SALTLIKE’, ‘CALMLY’, ‘BALDLY’, ‘HALFLIVES’, ‘SCALELIKE’, ‘STALKLESS’.

or that there is a separation of two words exactly behind the M+ symbols (e.g. PARTIAL ILLEGITIMATE – in fact there are many words ending on -AL and similar are there many words starting with either a vowel or a consonant followed by a ‘L as a second letter, too).

So if we ignore the words above (although still potential cleartext solutions), we should somehow focus on such a word structure. This gets us to the last three symbols of the phrase above, which acutally are consisting of a repeating 3-gram. Assuming that one to be a statistical non-outlier, actually gives us a structure of the second word as ‘.L…ING’ or comparable.

Update:
Here is a list of longer words, not complete but matching the ‘.L…ING’ structure…out of 1,200 trigrams combined with 1,500 words of length >7 (1.8m varieties) there are only 56 words that do comply with such a structure:

ALLEGATION
ALLEGEDLY
ALLIANCE
ALONGSIDE
ALTERNATIVE
ALTHOUGH
ALTOGETHER
BLESSING
CLASSICAL
CLASSROOM
CLINICAL
CLOTHING
ELABORATE
ELECTION
ELECTRIC
ELECTRICAL
ELECTRICITY
ELECTRONIC
ELECTRONICS
ELEMENTARY
ELEPHANT
ELEVATOR
ELIGIBLE
ELIMINATE
ELSEWHERE
FLEXIBLE
ILLUSION
ILLUSTRATE
PLACEMENT
PLANNING
PLATFORM
PLEASANT
PLEASURE
SLIGHTLY
ULTIMATE
ULTIMATELY
ALLOWING
BLEACHING
BLESSING
BLINDING
BLINKING
BLUSHING
CLAIMING
CLAPPING
CLEANING
CLEARING
CLIPPING
FLASHING
FLOATING
FLOODING
PLANTING
PLEASING
PLUGGING
SLAPPING
SLIPPING

Some risks with this thought..first the dictionary was chosen not too large (5,000 words only, which should be sufficient in a first step to continue the solving process). Second the trigrams were limited, althose the ones chosen are the most likely ones (to be present 2-3 times in the 340). Third, shorter words would match, too, have not been considered in this analysis. However, that’s it: If Z had used a longer word with + equal to ‘L’ (Bernoulli) – plus no outliers to handle – then the real cleartext could already be amongst one of the words above.

QT

Great work. Using conventional analysis, perhaps A is most likely to precede L.

But don’t forget specific Zodiac vocabulary tendencies.

ILIKE, KILL, KILLING, THRILL, THRILLING, WILL,etc.

Thus the M+ combo likely translates not as AL but as IL. Suggest try solving the M as an I and see what that yields. And to increase difficulty Z may spell words with three L’s in this manner KILLLING, THRILLLING, etc.

The letter "S" is an option..

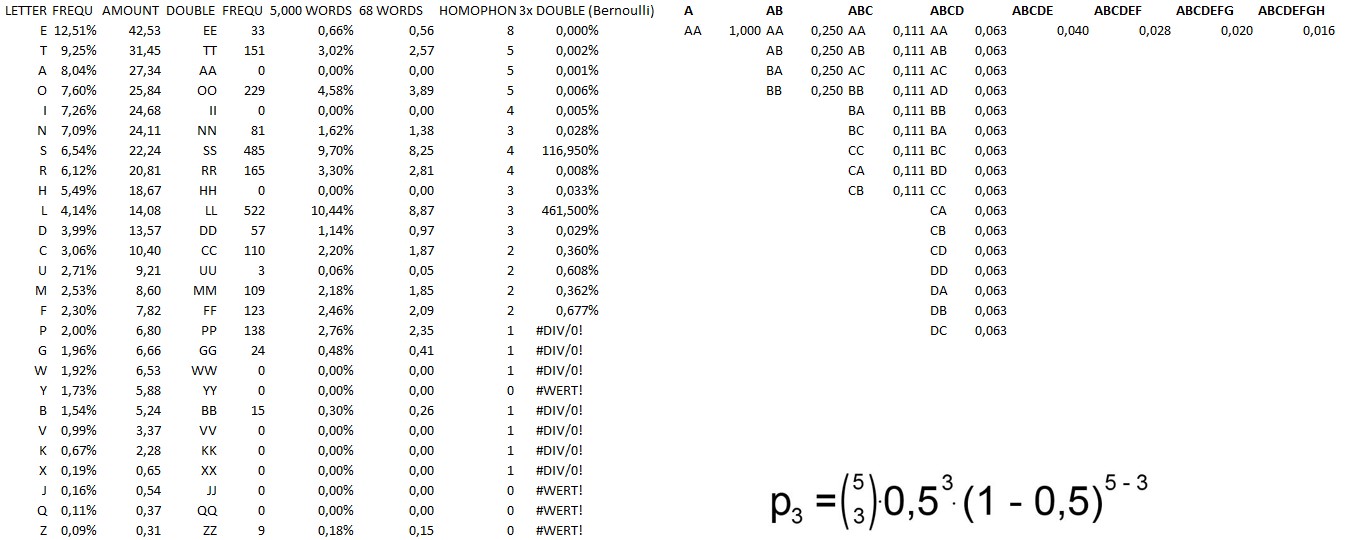
We already have seen the idea that the occurrence of double symbols (‘++’) may be compared to a bowl out of which we draw differently colored balls. For example if we have a non-frequent double letter such as QQ it is hard to get three double QQs. Opposite, with multiple homophones (e.g. for the letter ‘E’), chances of a visible occurrence of three double EEs wouldn’t be very likely either.

So what we in fact need to identify the + symbol is

a.) a letter that is somehow frequent (the + symbol occurrs 24 times in the 340, thus it should have at least a frequency of nearly 7%..better higher as there would be other homophones adding counts to its specific letter)
b.) a letter that occurrs frequently as a double letter (it should be expected to occurr at least once or twice in the cipher)
c.) a letter that is not represented by too many homophones (because these again would ‘hide’ the double letters somehow)

This could mean:
ad1.) the + symbol is most likely a letter such as ETAOINSRHL (all frequency approximately >4%)
ad2.) the + symbol is most likely a letter such as ETONSRLDCMFPGB
ad3.) the + symbol is most likely NOT a letter such as ETAOIN

Bernoulli’s formula allows us to combine the probability of a double letter occurrence with the amount of homophones used for a specific letter. To do so, the amount of ‘expected’ homophones is transformed into a separate table to simulate that each homophone would have been used e.g. equally (different homophones are used for the letter, thus the chance of two identic homophones appearing in a double letter is lower as a different homophone would in fact ‘hide’ the double letter). Of course this assumption is not fully correct as some homophones that represent one specific letter may be used more often than other homophones. However, the solution of the 408 shows that the homophones have been used quite equally (there in a sequence).

We do know that Z, in the 408, did not distribute homophones on his letters according to his own letter frequency (cleartext). Instead, he had used a separate letter frequency table. This table, however, must have been old or of bad quality as it must have had some outliers when comparing with modern frequency tables. If a modern letter frequency would suggest 4 homophones for a letter, Z had e.g. used only three homophones. Or, when comparing two letters, Z might have had used 2 homophones instead of 1 although the letter represented by one homophones was in fact more frequent in his own cleartext.

Subsequently, the following update was made:

1.) Considering Z’s different frequency table combined with a modern letter frequency table, thus a fictitious letter frequency table that would match Z’s actual homophone distribution in the 408 cipher.
2.) This frequency table was used to determine the amount of homophones for each alphabetical letter in the 340.
3.) An update of double letter frequencies was made (referring to a 5,000 word database and assuming an average word length of 4 letters)
4.) Bernoulli formula was used to determine if any letter is potentially a valid candidate to represent the + symbol

These are the results:

– Most non-frequent letters are ruled out as they either have a very low letter frequency or a very low double letter frequency (or even both). The only potential ‘candidate’ is the letter ‘P’, which would in fact occurr almost three times as a double letter (all of its occurrences then potentially represented by only one homophone..please note that homophones of <2 are not computable with Bernoulli as the formula always considers the chances which homophone is actually in use). However: P is not frequent at all. Instead it is highly unlikely that a 2% letter would occurr 24 times in a 340 cipher. Therefore we can eliminate the following letters as the + symbol: PGWYBVKXJQZ

– According to the double letter frequencies (!) most other letters would be represented by ‘too many’ homophones. So either the double letter frequency is too low or the amount of (expected, as used in the 408) homophones is too high (hiding the double letters, e.g. the case with ‘E’). The combination of both leads to chances of less than 1% that these letters are even able to represent the + symbol. Thus we can, with high chance, eliminate the following letters: ETAOINRHDCUMF.

– Only two letters are capable to combine a good relation between double letter frequency and an ‘adequate’ amount of expected homophones: ‘L’ and ‘S’. Bernoulli helps us with that one. This is in fact new information as in our previous analysis we had a 79% chance for the letter ‘L’ and an approximate 2.5% chance for the letter ‘S’. This had logically led to the conclusion that + is most likely represented by the letter ‘L’. With this updated data, however, we now have to realize that on one hand ‘L’ is a great candidate, the likeliness to appear three times in the cipher is in fact >1. But on the other hand, with the adapted (homophones to be expected) frequency table and an updated double letter frequency table, the letter ‘S’ is an absolutely viable candidate for the + symbol, too. In fact, both letters are expected to appear at least three times as a double letter in the cipher (although only one actually does, which may happen either accidentially or by purpose). Please consider that slight modifications do not alter this result drastically: For example it needs three times more TT double letters than expected to give it a chance of 34%. Four times more often and TT would be a valid + candidate, too. But this simply is not the case (in my reference data).

– Now deciding on which letter, ‘L’ or ‘S’, is representing the + symbol, we should have a look at the (single) letters’ overall frequency: ‘L’ is (usually) expected to occurr with a frequency of somewhere around 4%. Only one of three (or even four) homophones would thus cover almost twice than all of the expected ‘L’s. At least two additional homophones would therefore lead to an overall frequency of somewhere around 8%. Statistically unlikely, even if Z had used ‘LL’ quite often (statistically he would have done so with the SS letters, too). Different so with the letter ‘S’: This letter is expected to appear about 22 times in the 340 cipher – which is very close to the overall occurrence of the + symbol (24 times). Therefore, if the letter ‘S’ has been used only slightly more often, it is a way better candidate for the + symbol than the letter ‘L’.

One more comment: On same places in the cipher, two + symbols appear not directly next but quite close to each other. This may be due to one or two different words. If we assume at least one or two of those ‘structures’ to be represented by only one word: Out of 10,000 most frequent English words there do exist approximately 400 words containing two ‘L’s but there are almost 1,000 words containing at least two ‘S’..so the chances are as well that these structures do represent words with two ‘S’ instead of two ‘L’s.

Updated data: L and S are candidates for the + symbol

Structures of the + symbol..better for S than L?

There is not much statistical data on double letters. It could make sense to even analyse Z communication regarding his double letter usage..

REMEMBER…Z HAD USED THE DOUBLE LETTER ‘LL’ A DOZEN TIMES IN THE 408 – AND IT HAD SHOWED UP ONLY TWICE!

QT

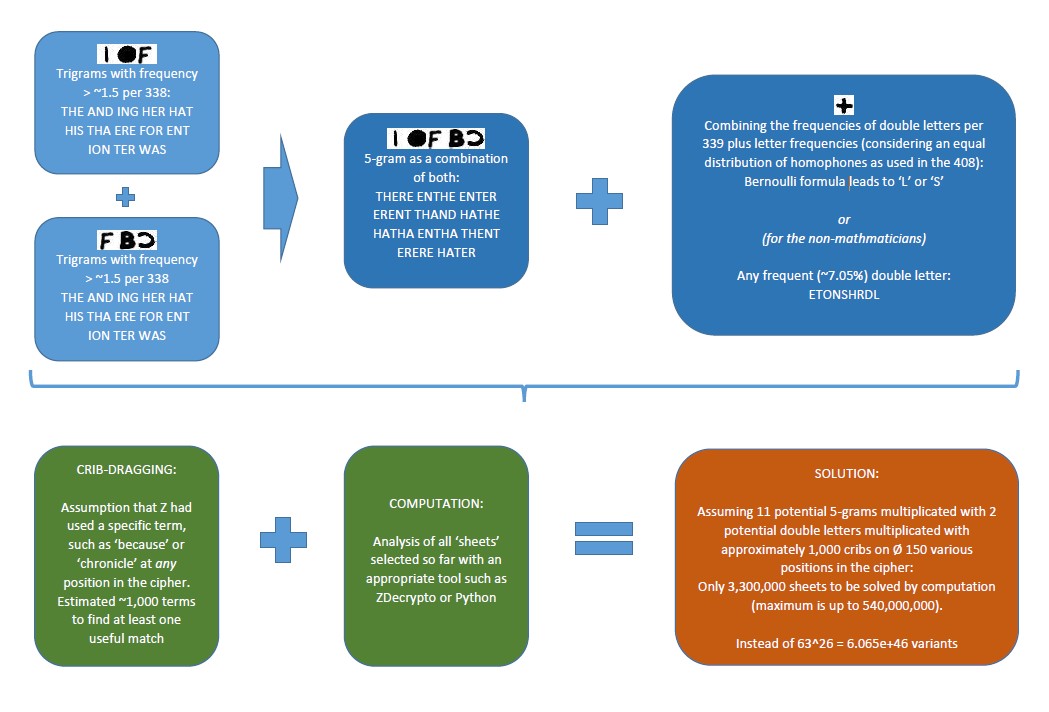
Long time no see..in fact never seen before: A solid approach of how to actually break the 340 cipher:

The message is the following: Trigrams such as QJF rather would not occurr twice in Z’s message. Two repeating trigrams, however, are available in the 340. Those even overlap on one position of the cipher, thus last and first letter of the trigrams must be identical. Based on this, there is also a double letter with an overall frequency of at least 7.05% occurring three times. We combine those two results. Then we use frequent terms such as the word ‘because’. If Z had used one of, let’s say 1,000 of such terms, it must be available at whatever position in the cipher. We combine this with the previous results. Therefore we do get multiple sheets based on the information above. These sheets shall be analysed by computation, eg. via Python or ZDecrypto or something like that. Due to the previous pre-selection, the whole cipher gets way better computable, the one correct sheet of only a few million sheets is easier to find than one in 6.05+e46 (billions, billions, billions…) variants.

This is how a preselected sheet looks like: Two trigrams with frequency >1.5 per 338 potential cipher positions, overlapping at the IoFBc position, combined with the frequent double letter ‘L’ and (this is new) the crib ‘because’ dragged on one of multiple positions in the cipher. As you can see, the sheet should be quite solvable for a computer. Of course, the computer has to check out all the sheets, not only this one.

IMO this is a quite secure method to crack the 340 (assuming it to be a homophone substitution, like the 408).

QT

As crib-dragging is a bit more complicated to set up, here are the results of another attack I currently try:

The first part is as described in the graphic above, thus aiming at two overlapping (repeating) trigrams. As some of the trigrams would be ‘hidden’ behind different homophones, those trigrams most likely occur more often than only twice. Regardless of that, we use any frequent trigrams that match together when overlapping (‘IoFBc’) and get a list of statistically interesting 5-grams:

‘THERE’, ‘ENTHE’, ‘ENTER’, ‘ERENT’, ‘THAND’, ‘HATHE’, ‘HATHA’, ‘ENTHA’, ‘THING’, ‘WITHA’, ‘WITHI’, ‘ITHER’, ‘THENT’, ‘ERERE’, ‘HATER’, ‘WITHE’, ‘ENTHI’, ‘ITHAT’, ‘THALL’, ‘HATHI’, ‘ITHIS’, ‘THITH’

Based on that, we may conclude according to our Bernoulli analysis that the + symbol represents either ‘L’ or ‘S’. Due to the overall frequency of the + symbol, we also may assume that + represents rather the letter ‘S’ than ‘L’. We now have a closer look at line 17/18 of the cipher:

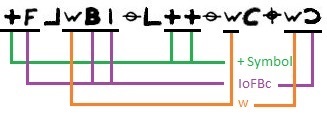
As you can see, by ‘guessing’ the w symbol, a total of 11 out of 16 letters are then defined. This ‘definition’ is no secure solution, however it represents the ‘most likely’ solution available (e.g. trigram QJF would rather not appear twice in the cipher, nor would a e.g. double letter M occur 24 times). Based on this, we simply complete the string of 16 letters with any other alphabetical letter (as we don’t know which ones those symbols acutally represent). We get:

5-grams x ‘+’ x ‘w’ x (A-Z)^4 = 22 x 1 x 26 x 26^4 = 6,796,147,072

therefore approximately 6.8B variants to check.

In fact, there are multiple approaches to ‘check’ this string:

a.) no complete cleartext word inside the string (e.g. a word longer than 16 letters)
b.) at least one word inside the string with e.g. length>4
c.) at least two words inside the string with e.g. length>4 (both)
d.) shorter words available, however only one word of length>4 available
e.) not even one word with length >4 available (only short words used in the string)

For practical reasons, I started with c.), thus searching for at least two words of length >4 inside the string (doing so by using an Aho-Corasick algorithm). Although tests are not finished yet, I could already check all variants for w symbol = E,T,A,O,I,N,R,H,D,L,U,B,G and + symbol = ‘S’ (using a smaller word database, btw..most frequent 2,000 words only).

Astonishingly there are only very few results. To be more precise, out of 6.8B variants it was possible to select approximately 140 strings only (!) that contain at least two words of a length>4 (~0,0000000206%). All other string combinations cannot produce an output of such two words of length>4.

Each ‘run’ for the w symbol (any alphabetical letter, eg. ‘B’) takes about 3-4 hours (Pentium quad core, Python). Currently the letter G is running through the program, cross-combining all 5-grams with ‘S’ as well as the word dictionary (all sort of simultaneously..).

ALL of the strings contain cleartext. Not always this cleartext makes any sense, of course, as any two words are found in the string, no matter in which context. The goal is to find the one string that supports us with the correct Z cleartext. Due to the small dictionary as well as some preconditions (e.g. + being ‘S’ instead of ‘L’ or the fact that we search for two words in the string), the correct solution is not necessary but imo somehow likely amongst the solutions below:

+=S, w=E
SAGENTWASSWEETED
SAGENTWASSWEEPED
SAGENTWASSWEPTED
SAGENTSASSSENSED
SAGENTSASSSENDED
SEVERELESSLEASEE
SEVEREWASSWEETET
SILENTWASSWEETEG
SILENTLESSLEEPEG
SEVEREHISSHEETEE
SAGENTHASSHEETED
SAGENTSASSSEEMED
SILENTLESSLEAVEG

+=S, w=T
none

+=S, w=A
SICATTLESSLAINAH
SEPANELASSLAINAT
SEPANELISSLAINAT
SIBATTLESSLAINAH
SICATTLESSLASHAH
SIBATTLESSLASHAH

+=S, w=O
SENORTHISSHOESOE
SAMONTHASSHOESOD
SEMONTHASSHOESOT
SEFORTHISSHOESOE
SENORTHASSHOTSOE
SENORTHISSHOTSOE
SAMONTHASSHOTSOD
SIMONTHASSHOTSOG
SEMONTHASSHOTSOT
SAMONTHISSHOTSOD
SIMONTHISSHOTSOG
SEMONTHISSHOTSOT
SEFORTHASSHOTSOE
SEFORTHISSHOTSOE
SEWORTHASSHOTSOE
SEWORTHISSHOTSOE
SEMONTHASSHOOTOT
SAMONTHISSHOOTOD
SIMONTHISSHOOTOG
SEMONTHISSHOOTOT
SAMONTHASSHOREOD
SIMONTHASSHOREOG
SEMONTHASSHOREOT
SAMONTHASSHORTOD
SIMONTHASSHORTOG
SEMONTHASSHORTOT
SAMONTHISSHOREOD
SIMONTHISSHOREOG
SEMONTHISSHOREOT
SAMONTHISSHORTOD
SIMONTHISSHORTOG
SEMONTHISSHORTOT
SAMONTHASSHOCKOD
SIMONTHASSHOCKOG
SEMONTHASSHOCKOT
SAMONTHOSSHOCKOD
SAMONTHISSHOCKOD
SIMONTHISSHOCKOG
SEMONTHISSHOCKOT
SAMONTHASSHOPSOD
SIMONTHASSHOPSOG
SEMONTHASSHOPSOT
SAMONTHISSHOPSOD
SIMONTHISSHOPSOG
SEMONTHISSHOPSOT
SEFORTHASSHOPSOE
SEFORTHISSHOPSOE
SEWORTHASSHOPSOE
SEWORTHISSHOPSOE
SENORTHASSHOWNOE
SENORTHASSHOWSOE
SENORTHISSHOWNOE
SENORTHISSHOWSOE
SENORTHUSSHOWNOE
SENORTHUSSHOWSOE
SAMONTHASSHOWNOD
SIMONTHASSHOWNOG
SEMONTHASSHOWNOT
SAMONTHASSHOWSOD
SIMONTHASSHOWSOG
SEMONTHASSHOWSOT
SAMONTHISSHOWNOD
SIMONTHISSHOWNOG
SEMONTHISSHOWNOT
SAMONTHISSHOWSOD
SIMONTHISSHOWSOG
SEMONTHISSHOWSOT
SEFORTHASSHOWNOE
SEFORTHASSHOWSOE
SEFORTHISSHOWNOE
SEFORTHISSHOWSOE
SEFORTHUSSHOWNOE
SEFORTHUSSHOWSOE
SEWORTHASSHOWNOE
SEWORTHASSHOWSOE
SEWORTHISSHOWNOE
SEWORTHISSHOWSOE
SEWORTHUSSHOWNOE
SEWORTHUSSHOWSOE

+=S, w=I
SANINTHASSHIRTID
SANINTHASSHIRTID
SININTHASSHIRTIG
SENINTHASSHIRTIT
SANINTHISSHIRTID
SININTHISSHIRTIG
SENINTHISSHIRTIT
SANINTHUSSHIRTID
SININTHUSSHIRTIG
SENINTHUSSHIRTIT
SEBIRTHASSHIRTIE
SANINTHASSHIFTID
SININTHASSHIFTIG
SENINTHASSHIFTIT
SANINTHISSHIFTID
SININTHISSHIFTIG
SENINTHISSHIFTIT
SANINTHUSSHIFTID
SININTHUSSHIFTIG
SENINTHUSSHIFTIT
SEBIRTHASSHIFTIE
SEBIRTHISSHIFTIE
SEBIRTHUSSHIFTIE
SANINTHASSHIPSID
SININTHASSHIPSIG
SENINTHASSHIPSIT
SANINTHISSHIPSID
SININTHISSHIPSIG
SENINTHISSHIPSIT
SEBIRTHASSHIPSIE
SEBIRTHISSHIPSIE

+=S, w=N
none

+=S, w=H
none

+=S, w=R
SHAREIPASSPRIORR
SHAREIPISSPRIORR
SHOREIPASSPRIORR
SHOREIPISSPRIORR
STHREEPASSPRIORR
STHREEPISSPRIORR
STOREHEASSERVERR
STOREHEISSERVERR

+=S, w=D
none

+=S, w=L
none

+=S, w=U
SECUREPASSPURSUE
SADULTLESSLUMPUL
SECURELESSLUMPUE

+=S, w=B
none

+=S, w=G
still running…

…

QT

Some more thoughts about the cipher..

In fact there is one big difference between the 340 and the 408: Although the 340 cipher text is shorter and contains more homophones, the + symbol is somehow outstanding as it appears an overall of 24 times or 7% while in the 408 the maximum count for one homophone is 16 or 4% only. Now this leads to a lot of trouble BECAUSE if we assume the + symbol not to be the only homophone for a letter, it would indicate a letter frequency of much more than 7%. Lets think about it:

Letter E: At least 5 if not 8 homophones, if sequentially used that would lead us to a letter frequency of roughly 5 times 24, thus 120 or 35%, which is unrealistic.
Letters L, T, N, O, A etc similar, assuming 3 homophones only, leading to a letter frequency of 21%.
Letters H, P etc., assuming 2 homophones only, leading to a letter frequency of – still – 14%, all of this is sort of unrealistic.

In addition to the trivial thoughts above I tried to recalculate the probability for a letter to show up three times as a double homophone. Most likely the L can be illustrated to be represented by the + symbol, however this still requires one of the homophones to represent 7% of the cipher. But we must accept that there would be two more homophones, most likely as frequent as the + symbol, so it doesn’t work out no matter how hard someone tries (because the other homophones ‘push’ the overall letter frequency above normal levels).

So I have to admit, although other thoughts were present earlier, that – after applying a binomial tree with hypergeometric distribution values – there are only three ‘candidates’ of frequent letters that may fulfill the criteria to match the three double ++ formations (Z-408-frequencies):

S – 16.7 expected letters: 34.4%
L – 27.5 expected letters: 7.2%
O – 22.4 expected letters: 21.9%

The letter E, for example, had

E – 44.9 expected letters: 0.07%

To calculate the letter S, it was even necessary to set the minimum of present double letters (SS) in the cipher to an expected minimum of 6..on the other hand it was not yet possible to complete the calculation for more than three double letters (‘draws’). Thus the values above are only approaches (so far I could not find any formula for hypergeomatric permutation over multiple draws..assume a bowl of different homophones drawing two symbols each time..what are the chances to draw 1, 2, 3, 4 etc. times to get at least 3 pairs of ++ ..even with such formula we still couldn’t tell how many double letters are present in the cleartext).

What the observation above shows, however, is that it is very unlikely that any letter with multiple homophones is present in the cipher with 24 + symbols. Not only that those cover already 7% of the cipher but the other homophones representing the same letter have not even been considered yet. Even if the + symbol represented the letter L, there would be more homophones representing L – leading to a way too high value for the L letter frequency. Similar with O, only 22.4 letters are expected but already one of at least 3 homophones does represent 24 letters.

My conclusion to all this is that no matter how you look at it, a multiple (>2) homophone letter doesn’t work out here at all. Also the letters with 2 homophones don’t work as they would at least be present with 10% in the cipher (e.g. 30 letters, 24 of them a + symbol).

If we now look back to the 408, the maximum symbol there was the reversed Q symbol with 16 or 4%. Although the cipher text was shorter AND there had been fewer homophones!!

So there are two possibilities..we either can wonder about such high presence of one single homophone OOOORRRR due to the cleartext it was absolutely inevitable to use those 24 + symbols. The only case I can think of is the case that the + symbol represents a letter which is present with ONE homophone only.

Now those would rather not be the letter Q or K etc..as they are commonly not present as multiple double letters. But there are other medium-frequent letters represented by one homophone such as C, M, P, G. Of those the letter M is expected to be one of the most frequent and indeed: The most frequent symbol of the 408 cipher was represented by nothing else but the letter M!

What I’d like to say is that it is very unlikely that any frequent letter is represented by the + symbol. This is also the reason why there is no sequence possible between the + symbols (three pairs of them occur directly after another, two with one homophone inbetween +b+). If we count the reversed Q in the 408, we get 16. In that case, however, the reversed Q or (M letter) was present with a normal frequency. If, however, such single-homophone-letter had an unexpectedly high frequency, such as 7% instead of 3%, this particular letter could be the cleartext behind +.

According to this, the letters C, M, P, G are – although above average frequency – the best candidates for the + symbol.

With double letter frequencies of

C: 0.12
G: 0.01
M: 0.05
P: 0.26

the letter P is the best double letter candidate, while the letter C is in fact closer to the overall frequency of 7%. Thus, depending on the cleartext anormalities, it is still absolutely inconclusive to tell which of those single-homophone letters shows up three times as a double letter (it could be anyone..) – and has an above average overall frequency.

QT

News with the cipher from my side..let’s assume that IoF and FBc (the IoFBc section I had mentioned earlier) are frequent trigrams (as both appear at least twice in the cipher). This leads us to IoFBc most likely being one of the following 5-grams:

‘THERE’, ‘ENTHE’, ‘ENTER’, ‘ERENT’, ‘THAND’, ‘HATHE’, ‘HATHA’, ‘ENTHA’, ‘THING’, ‘WITHA’, ‘WITHI’, ‘ITHER’, ‘THENT’, ‘ERERE’, ‘HATER’, ‘WITHE’, ‘ENTHI’, ‘ITHAT’, ‘THALL’, ‘HATHI’, ‘ITHIS’, ‘THITH’, ‘THERS’, ‘HEREA’, ‘HATIO’, ‘ERERS’, ‘ERESS’, ‘FOREA’, ‘THATI’, ‘THATE’, ‘THAVE’, ‘TIONE’, ‘TEREA’, ‘VEREA’, ‘WITIO’, ‘WITER’, ‘ATING’, ‘ATION’, ‘ATITH’, ‘ONERE’, ‘ONENT’, ‘ONERS’, ‘ONESS’, ‘ATERE’, ‘ATENT’, ‘ATERS’, ‘ATESS’, ‘REAND’, ‘REALL’, ‘REATI’, ‘REATE’, ‘REAVE’, ‘NCERE’, ‘NCENT’, ‘NCERS’, ‘NCESS’, ‘AVERE’, ‘AVENT’, ‘AVERS’, ‘AVESS’, ‘OFTHE’, ‘INTHE’, ‘OTHER’, ‘ONTHE’

This, however, also leads us to the idea that the (repeating) bigram BY is not only frequent, too (as it repeats as well), but also do we get the first bigram letter from the list above. An example: If THERE is representing the 5-gram (IoFBc), then the B symbol is representing the letter ‘R’. With that information we can look for frequent bigrams starting with ‘R’, e.g. RE, RO, RA, RI, RU, RT, RS, RD, RG. Due to BY repeating, it most likely is not representing e.g. RM.

Based on the list above, the B symbol represents one of the following letters only:

A, E, H, I, L, N, O, R, S, T, V

BECAUSE both repeating trigrams of the 340 cipher with a high chance are not non-frequent, the BY bigram is supposed to start with one of the letters above. Therefore, BY most likely does not represent any other bigram than those starting with one of the letters above. As BY also occurs more than once, BY is a frequent bigram (and not an accidentially repeating non-frequent bigram), too.

The letters B, C, D, F, G, J, K, M, P, Q, U, W, X, Y, Z may rather be eliminated for the B symbol.

DEPENDING on which 5-gram is assumed to be correct, the BY is partially pre-determined, too. For example:

IoFBc: THERE
BY: RE, RO, RA, RU, RI, RT, RS, RD, RG

The combination of THERE and DE, for example, is impossible as in that case one symbol would represent two different letters (assuming a homophone substitution).

In combination with e.g. Bernoulli’s result regarding the + symbol, same can be done with the M+ bigram of the cipher (repeating three times). If one assumes the + symbol to represent the letter ‘S’, the M+ bigram would be AS, IS, US, DS, TS etc. (a frequent one, too). In any case, the bigram would end with S.

Altogether it can be said that by this procedure, the n-gram, the Y and the M can be defined as some sort of scale. Those eight symbols already represent 85 of 340 letters or 25% of the cipher!

QT

Looking closer at the lines 3/4 and 9 of the 340 cipher:

As we can see, some homophones actually show up in both of the sequences. Further, some homophones are part of repeating bigrams/trigrams or the + symbol.

Assuming that only frequent bigrams/trigrams are capable to show up at least twice (or more often) under multiple homophones per letter, I’ve set up some strings of input variables (approx. 185,000) that allow to set up 90% of both of the strings shown above. Latter done so mostly to avoid memory errors in python..now the program takes more time but the pc can handle it ‘one by one’. For testing reasons, the + symbol was set as ‘S’, due to previous Bernoulli analysis (may be changed anytime).

For the first time ever, currently two FCCP strings are cross-checked to each other (cracking process). A third string could be added sooner or later.

Here are some of the first results..please be aware that not necessarily each string is correct, however it shows that e.g. two words of length>5 can be found simoultanously in two different strings:

..
DROZEESTOOPED ESYSOONEREO
..
GREOEESHINING ESUSINGEREE
..
EROZEESISTERE ESJSSPHEREO
..

Advantages:
– found solutions cover 140 out of 340 homophones (>41% of the cipher)
– method works if no bigram/trigram is statistical outlier
– method can be extended to a third string (final cracking)

Disadvantages:
– if variables are wrong (statistical outliers), method may fail
– only dealing with homophone substitution
– not considering dyslectic errors
– potentially high analysis effort (e.g. if + is not representing ‘S’)
– currently searching for words of length>5 letters only

QT

UPDATE:

The first run brought too many results, I stopped at approx. 650,000. This, of course, is naturally occurring if we think about the variety of input data (~185,000).

To narrow down the cracking process, a third string from the cipher has been added (line 17/18 from + to w symbol). Now, the prog has to find a total of three words in three different strings (at least one word in each string).

As you can imagine it is not easy to simply type three words into the cipher (e.g. Oranchak’s great webtoy) without getting any interferences. It might be easy at some spots of the cipher, but not in those three strings (as they have many homophones in common).

The program is still running (and could do so for a long time..).

However, if there is a match it might already be part of Z’s cleartext (no anagramming or other ‘compromises’). Due to the cross-checking over three different ‘areas’ of the cipher, chances to hit an erroneous peak are very low. It still is possible, however, that e.g. one string does not contain any word of the length>5. A next step could be to expand the dictionary to cover e.g. 4-/5-letter words, too.

SUMMARY:
– checking Bernoulli test on letters for the + symbol
– checking the most frequent repeating (overlapping) trigrams (5^2)
– checking the most frequent repeating bigrams (28^5)
– trial & error with ‘fillers’ by using A-Z (26^5)
– trial & error with one filler (‘w’ symbol) by using ETAOINSRHDLCU (1×13)

This leads us to 1 x 5^2 x 28^5 x 26^5 x 13 or 66 Quadrillion variations being checked against a 5,000 word database for (multiple) cleartext occurrence.

Although I guess we might get old on waiting for this one, it might (!) be the only way to actually solve the 340. No need to underestimate the complexity of the 340 cipher at this point.

However, the set-up has at least partially been chosen in a way that the most likely combination will be calculated first (e.g. ETOINSRHDLCU for the frequent ‘w’ symbol). Therefore a solution might come up earlier than expected.

Also, the computation process can still be broken down into parts, like it has been done by choosing the letter ‘S’ for the + symbol. Of course, the speed of the pc as well as Python itself also play a role in this anti-Z game. Hopefully, Python does some efficiency tricks in the background, too.

While doing so, it should be mentioned that if the prog finds multiple solutions for the three strings, the first solution is most likely the correct one. Thus, it might only be necessary to calculate e.g. 0.000001% of all variations to find Z’s cleartext. If a solution is found, it then covers a total of 154 symbols or ~0.45 of the cipher. For a human being it then will be easy to either solve the rest of the cipher or to discard the solution as an erroneous, accidential peak.

We’ll see if we get any promising results, I’ll keep it updated. If anybody has access to a supercomputer, it weren’t such a bad idea either.

For those interested, the following is a small part of the 157-line Python prog..it covers two out of three strings. Various settings such as the dictionary or the import from the input data file is not shown below nor is the Aho-Corasick algorithm to search efficiently for words.

    for P, Q in [(P,Q) for P in alphabet for Q in alphabet]:
        chain2 = M+pl+P+pl+Z+Q+O+F+B+c+Y
        if int(len(get_keywords_found(chain2))) >0: ## Minimum Keywords in chain2
            for S, R, T in [(S,R,T) for S in bigrams2 for R in alphabet for T in alphabet]:
                chain1 = S[1]+B+Y+R+c+M+pl+U+Z+G+T+S
                if int(len(get_keywords_found(chain1))) >0:

QT

seriously thinking about setting up my second PC for the computation of Z’s 340 cipher..

Update…adding a third string on the first run didn’t work, computation way too slow..however the program works with cross-checking two strings. More results, some almost-duplicates due to conjugation of all variations. Below you can see a 30 sec. video how the results pop-up. No interferences regarding the use of homophones. All results are based on a length>5 dictionary with approximately 5,000 words as well as some pre-setting of variables (185,000 different settings of approx. 10 different homophones..results shown in the video are around #38,000 of those 185,000).

https://docs.zoho.com/file/5hf3946ba379 … 041b47be38
(~33 MB)

The tool develops to be very efficient as the results found can be re-checked against a different third string in a second step (and so on..) until a final solution is found. If no solution is found, that either means that the pre-settings were wrong or the words weren’t present in the dictionary or that at least one string does not contain any word of length>5 (which is our biggest trouble, so far). Pre-settings of the variables may be modified, however. Thus, all potential settings can be checked, e.g. the + symbol representing another letter than ‘S’.

As soon as a solution is found with e.g. three (or more) >5 letter words in three different strings, it could already be close or equal to the cleartext solution.

QT

Why did you abandon the results of your first study, which showed that L was the letter most likely represented by + ?

In the English language, perhaps T or S are more commonly doubled, and more frequently used. But looking at Zodiac’s particular language, as revealed in his letters and the solved 408 code, showed he most frequently doubled L and used L very often. This showed up in your first study, and was reinforced by Glurk, Doranchak and myself presenting all the words that Z used with L and LL.

Bernoulli computation showed that the odds for + being a highly frequent letter are very low. This because if Z had used more homophones for frequent letters, the occurrence of double letters would get ‘shuffelled’ too much due to the amount of homophones used.

Less-frequent letters might be represented by three double occurrances but those letters do have the problem that they wouldn’t occurr with an overall frequency of >7%.

Thus, the truth is somewhere inbetween, Bernoulli can show exactly where. The following sheet is simplified but after having done such calculation you can see the following:

– Rare letters might be an option, however usually do not occurr with a frequency of 7%
– Frequent letters might be an option regarding the frequency, however get shuffelled too much by the use of multiple homophones.
– Most letters don’t even have a sufficient double letter frequency (e.g. the letter ‘I’)

SOME letters do remain with an even low chance to be represented by the + symbol. It is not very likely that three double symbols occurr in such a cipher at all!! The chance for this is only around 10%!

Such letters are – actually only two – ‘L’ and ‘S’. Of those two, the ‘S’ is closer to a frequency of >7% which is why I (meanwhile) do prefer the letter ‘S’ over the letter ‘L’. In fact, the frequency of >7% actually correlates better with the average frequency of ‘S’, too (which gave me some confidence in the idea of ‘S’). Also, ‘S’ is a valid candidate for frequent double letters.

Nevertheless: ‘L’ still has a similar chance (but then must have been used with an above-average frequency..therefore, assuming a 408-like distribution of homophones, the + symbol – most likely – represents the letter ‘S’). All just my humble opinion.

BTW, the only three letters being expected to occur more often than three times as a double letter are ‘S’, ‘L’ and ‘O’. In a 340 text, the letter O is expected to occur approximately three times (it has too many homophones, too). ‘S’ and ‘L’ both are expected to occur approximately 7 times. All others are not expected to occur even three times or more at all. Considering the shuffling with homophones it therefore is obvious that the ‘L’ and the ‘S’ are sort of the only candidates (if ‘normal’ language has been used..no pizza in nizza stuff..) for the + symbol.

QT

Well we have had this debate before. I still maintain your excellent initial work and resulting conclusion that L was likely the correct solution for the + symbol was correct.

I think it is very important. When you consider that if + is L, so the many ++ are LL, that could lead one to consider solving the symbol before the ++ as likely an I or an A, and you try word solves from there. Really if you misidentify the + symbol, you have 7 to 8% of the code wrong at the start, and you will never solve it. If you correctly identify the + symbol, you finally have a start, and if correct, you have 7 to 8% of the code solved, and can start to do more word solves from there. And yes I agree there is likely some other second step needed to fully solve the code. But after almost 50 years of getting nowhere, can we try to solve ONE symbol of the 340 code, the symbol that appears most frequently?

I would downplay what studies and probabilities for the English language in general show. What letter is more commonly doubled in novels or general writings means little. The letters doubled and the letters that were used in the previous Zodiac code and the previous Zodiac mailings are what should be paramount and take precedence.

Because not only is LL a combination that occurs often in normal English language usage, the Zodiac in particular used the LL combination more than any other. Look at this past work for reference, with comments from myself, Glurk and Doranchak. In terms of solving the first stage of the 340, I agree with your initial study and finding very much that as a working hypothesis it makes very strong sense to solve ++ as LL.

AK Wilks:

In the first Zodiac Code he used "S" 24 times. Only once was there a "SS", and that happened in the phrase "it iS So much fun". Zodiac never used a word that has "SS" in it, not once. Compare that to the number of words he used in the first code that had "LL" – SEVEN different words! And they are words we might think it is likely he also used in the 340 code. They were:

Zodiac also used these words with a single "L". – like, people, wild, girl, slaves, slow, animal, afterlife.

By my rough quick count, the letter "L" appears 33 times in the 408 code. About 8.1% of the letters are "L", which is about double normal usage, as it happens that many words Z liked to use have either L or LL in them. So if Z used "L" 8.1% of the time in the 408, it seems to me that solving + as L, meaning L is used 7-8% of the time in the 340 code is right on target.

GLURK: I’ve done a small bit of work on this, and I’m going to have to say that as far as Zodiac’s use of the doubled letter "L," he did in fact use it a lot.
More than would be expected in normal writing. Even in words that, properly spelled, would not have the letter doubled.

I did not do exact word counts, sorry, but in a quick study I’ve found:

ALL, ALLREADY
AWFULLY
BILLIARD
BILLOWY
BULLET
BULLSHIT
CALLED
CELLING
COLLECT, COLLECTING
CONTINUALLY
FILLING
FULL
HELL
HILL, HILLS
HOLLY
KILL, KILLED, KILLER, KILLING
PULLED
REALLY
ROLLED
SHALL
SMALL
SQUEALLING
TELL, TELLING
THRILLING
TITWILLO
UNTILL
VALLEJO
WACHAMACALLIT
WALL
WELL
WILL

This should be all of them, I think, unless I missed something… I probably did miss something…
I don’t, however, believe that the 340 is simply a homophonic cipher like the 408. But I also don’t have any doubt at all that Zodiac often used "LL" in his writings. He clearly used it more than would be expected.

DORANCHAK: Here are some others:

ALLEY (confession letter)
ALLEYS (confession letter)
ALLWAYS (1971-03-13-times)
BALL (confession letter)
BELLI (1969-12-20-melvin-envelope)
CALL (confession letter, 1969-11-09-chronicle, 1970-07-26-chronicle)
CELL (1970-07-26-chronicle)
FALL (1970-06-26-chronicle-cipher)
FELLOWS (1970-07-26-chronicle)
FOLLOWED (confession letter)
UNWILLING (desktop poem)
SPELL (1974-02-14-sla)
SPILLING (desktop poem)
WILLING (confession letter)
WILLINGLY (confession letter)
YOULL (1970-10-05)