Interesting theory. However, it might be more conclusive if you were able to create a homophonic cipher using this method that cannot be solved by hill-climbing. It seems to be a very effective technique.

-glurk

Sounds like an idea for a masters thesis. I really like the discussion about the cycles, and how you identified the different ways that they appear and named them.

I have wondered why the 340 cycles are not as perfect as the 408 cycles, and if Zodiac used some simple paper and pencil way to cycle the cycles ( regional cycling ).

One idea that I was working on this last spring, before getting sidetracked with other projects, was to find some visual way to identify an overall "signature" for cycle activity and the presence of regional cycles.

See below for a rough example. On the left, positions in the 340 where perfect three symbol cycles begin. For example, 30 such cycles begin at column 13, row 7. And 24 such cycles begin at column 4, row 8. The spreadsheet is a heatmap of cycle start and stop activity. On the right, positions in the 340 where perfect three symbol cycles end. For example, 25 cycles end at column 5 row 10 and column 5 row 13. Examples marked with heavy blue squares.

So this is just a very rough idea. But you could use it or something like it to identify a "signature" for the 340 for two, three, four, etc. symbol cycles. Then use your computer to make a lot of homophonic messages with a lot of different samples of plaintext and a lot of different types of cycles. Look at the signatures for your test messages and compare with the 340’s signature. It could help us guess what Zodiac did. I would like to continue this type of work in the future.

I think that you should look at some of the other statistical facts about the 340 before getting too involved with your bigram work. See this? There are only a few of these symbols but yet they arrange together into a pattern. That bigram pattern can be found throughout the 340, and there are many more of them than there are bigram repeats where the symbols are positioned next to each other.

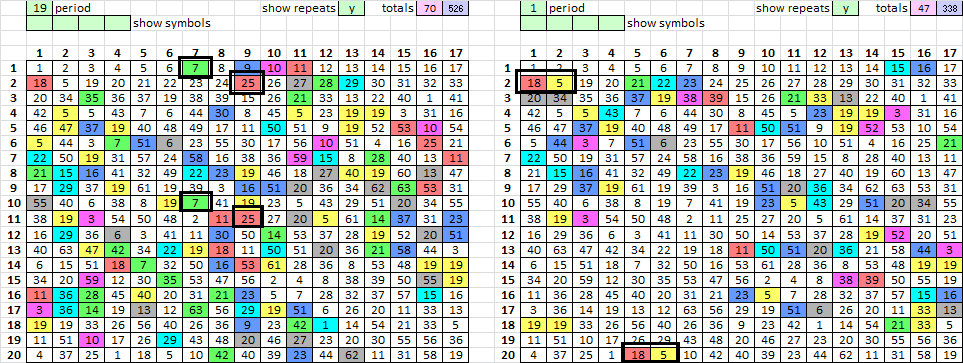
I use numbers instead of symbols for my spreadsheet. Here are all of the "period 19" repeats, on the left. Find the individual ones with color matching. I marked an example with heavy black square. They take up about a third of the message. You should talk about them in your analysis. On the right are the "period 1" repeats. Another example marked with heavy black square. There are a lot more period 19 repeats than there are period 1 repeats.

Thanks for the post.

Moonrock, thanks for taking the time to post all that. There are a lot of interesting ideas in there. I agree with glurk — it would be very informative to produce test ciphers (sticking to simple homophonic substitution in the normal reading direction) that cannot be solved using current hillclimbers. Such ciphers are known to exist but rely on the plaintext having anomalous n-gram statistics (for instance, lists of places or names, or of spelled-out numbers). I’d be surprised if a plaintext with normal n-gram stats could be protected from a hillclimber’s attacks simply by changing the cycles and/or bigrams, without resorting to transpositions or other schemes (and obviously without increasing the number of unique symbols).

—

Thanks for sharing your test cipher. I’ve added it to my collection of test ciphers:

https://docs.google.com/spreadsheets/d/ … sp=sharing

In that spreadsheet I compare hundreds of test ciphers to Z340 via many different measurements. When sorting by similarity to Z340, your cipher appears on row 19, which means you did a good job of making it very similar to Z340, based on calculations of the overall distance of its measurements to those of your cipher.

I don’t yet know a good way to deal with the anomalous sequence problem. I wonder if it is even possible to develop a sufficient enough language model to capture such anomalous sequences. Your bigram chaining idea is interesting and I wonder if it would generalize to more kinds of repeating sequences such as bigrams that are separated by wildcards (A?B A?B instead of AB AB, where ? can be any symbol).

—

Hi, happy to have joined the forum.

I am looking at the Test Cipher Collection https://docs.google.com/spreadsheets/d/1awBaW_1GC3TWgRmOwKnYKwOLvBY5unkX7P1yt1itMiA/edit#gid=1394933925, and trying to solve those marked as unsolved.

I believe I have a solution to this challenge. There might be a couple of errors but it is something like.

IHAVENTFORGOTTENABOUTTHEPIGGIESWHOMADEAFOOLOFTHEMEELVESTRUTHFULLYONEDAYIMAYPAYTHEMAVISITTOSEEHOWGOODTHEIRMEMORYISAVERYTOOSINCEHETHINKSIMADAMNQUEERHOWFUNWOULDITBETOTALKTOHISFACEWITHOUTHIMEVENKNOWINGITSSFSFAVORITESUPERHEROTHERODIACBYTHEWAYTHATBROADYOUFOUNDDOWNSOUTHWASMYFIRSTITWASSUCHAGREATPLEASURETOTEACHHERALESSONBUTNOTASMUCHASSFPDRLORPWKFE.

Was it already solved?

George

Welcome Dr.G,

Below is the link to introduce yourself. If you would like to create a new topic and post a little about yourself, if you wish.

viewforum.php?f=20

trav

Was it already solved?

Yes, it was solved. And welcome.

Thanks Jarve – also posted in ‘introduce yourself’.

Are there challenges which are pure homophonic (no transposition etc…) which are still unsolved?

George

Did this one ever get solved?

http://www.zodiackillersite.com/viewtop … 612#p42612

It’s difficulty is apparently due to high multiplicity (0.438)

Are there challenges which are pure homophonic (no transposition etc…) which are still unsolved?

Try https://ciphermysteries.com/2017/06/25/ … hers-solve

Did this one ever get solved?

No. I have this cipher as alanbenji. I suspect that its high multiplicity is not the only problem. The underlying plain text may possibly be a bit strange.