On deeper consideration it will be noted that, whilst intended to be helpful, the above analogy is not, however, a perfect one. In the context of a chess problem, the ‘constraints’ that lead inevitably to the solution are precise. They derive from a combination of 1.) the rules of the game of chess, 2.) the actual position as encountered in the problem and 3.) knowledge of the intended outcome (checkmate next move). This is not, however, the case in relation to the ‘cipher-as-problem’. In this latter case, whilst you have the ‘position’ (the cipher code), there are unfortunately no rules to accompany it. You may have some significant insight into at least the nature of the outcome, such as that we know the solution to the Z32 will give the location of a bomb, but such fore-knowledge will at best be open to variations of interpretation, at worst sketchy and ill-defined. Thus, as relates to whatever constraints we must expect to find, we are here going to have to initially infer them, and test them later. That said, our initial inference has to be that such constraints must be present, in some form or another, else we are sitting on the fence and at risk of trying to solve a problem when we are actually involved in a game of chess with a presumed opponent who has every advantage over us and who must win.

In the next post, I will try and present an example to illustrate a reasonable approach to how such potential constraints may be identified and inferred.

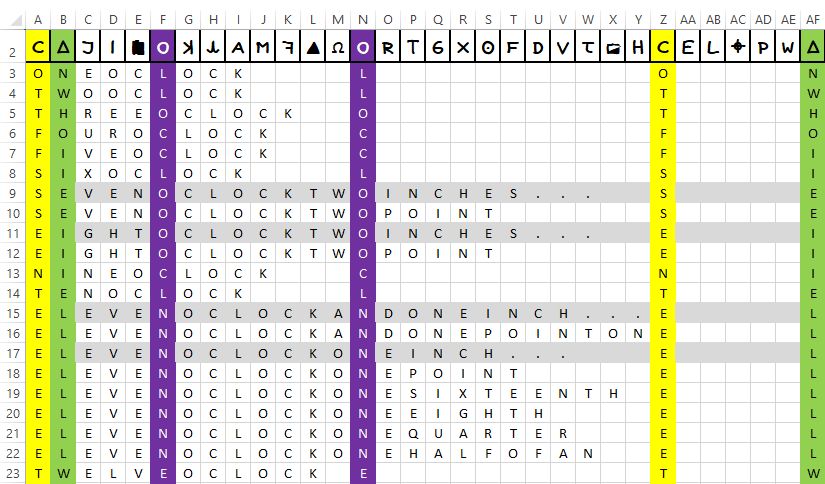
Consider the Z32, which is reproduced below with additional highlights intended to colour-code where the few duplicates are set.

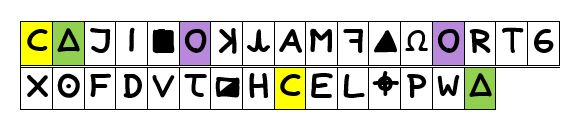
Obviously, in the absence of wanting to propose a polyalphabetic substitution cipher is in play, of their very nature the duplicates present constraints such that these three paired locations in the plaintext must be filled by three corresponding paired letters.

But then, it has to be asked: why these pairs specifically? Undoubtedly, on the likelihood that at least one or more of the three respective plaintext letters are common in the English language, what intention may be behind why these instances of a given letter specifically were set under the same cipher character, when there are likely other instances of the same letter alternatively encoded?

We cannot, of course, give any definitive answer to this question, particularly at this point. However, should we later produce a potential solve that has these duplicates fall alternatively on either the beginning or the end of certain words, could we not then work back to suggest that this choice of duplicates was thereby potentially intended, essentially in the manner of a helpful constraint? Possibly.

The open triangle itself gives illustration of potentially a different level of constraint. It would not be beyond reason to suppose that this particular symbol — one which relates the very last letter of the cipher to the second letter of the very first word — is intentionally duplicated for the very reason of constraining both the selection of candidate words at the start and, in consequence, what word goes at the end.

On the fair assumption that the first word is going to be an integer number from (possibly) ‘ZERO’ to ‘NINE’, this would mean that the last letter of the cipher must be one of ‘E’, ‘N’, ‘W’, ‘H’, ‘O’, or ‘I’. But could there be an even deeper constraint than this? Could it be that this last letter just happens to be one that, of itself, severely constrains the possible words that fit at the end — ‘I’, for example, as opposed to an unhelpful ‘E’ — and that the very purpose of duplicating this from the second letter of the cipher is to enable “get the first word, and you’re well on your way to the last?”

However it is — and this is just one example of the application of reasonably inferred constraints — if there is nothing of this sort at all, intentionally provided for the very purpose of aiding us in our progress towards probable candidate solutions, then I would contend that we had better spend our time elsewhere in some more profitable pursuit. Without constraints of some kind, in a cipher that presents 29 distinct characters out of 32, there would be nothing to make progress with. Likewise, the Zodiac might just as well, in that case, have used a full 32 distinct characters and been done with it.

Only, he didn’t.

We just have to work out why he gave us what he did, and how that helps us along our way.

Posted by: @shaqmeister

Is the Zodiac playing a game with you that, like in chess, it is his intention to win, or is he setting a problem for you, that you are expected — not without considerable effort, however — to ultimately solve?

Too often do we see attempts setting out to solve the remaining ciphers where this necessary initial decision has not even been made.

So, are we enjoined in some fierce and unending battle that we have already lost, or have we been set a problem to be solved? Because, it matters which!

Depending upon which choice we make, the consequences of the one could not be further from those of the other. Sitting on the fence is not an option, particularly with a pair of ciphers as short as the last two. If we do not find something, of whatever nature, that must of necessity lead us on the way to a unique solution, then either the Zodiac has tried to help us and fallen short, or we are lost on the battlefield before even striking a blow.

And just to be clear, what I am wanting to convey here is my personal conviction that it is this very posture of ‘fence-sitting’ which ultimately contributes perhaps the biggest obstacle to success of all — if, that is, success is there to be had. No one says it has to be, of course.

”Here’s my amazing solution of the Z32 code which, despite the fact that the Zodiac employed every trick imaginable to hide from me, I was able to crack and see right through all the levels of obfuscation” will always be a non-starter. If he did, in fact, aim to hide the solution that well, then forever hidden it will be. Well done. You just spent your hours attacking a problem that, from the very nature of your assumption as to the composer’s intent, can only be unsolvable. Mind the splinters when you sit down.

”Here’s a potential solution that tries to just keep as close as possible to what it would be fair to presume we are being told — or instructed — to do, and using just what we’re given.” And sure, the solution offered may not turn out to be a uniquely defined one, but at least the effort is honest and the proposal likely a better one.

”Here’s a candidate solution that follows a method of solution that would appear to be strongly indicated by the context, and which benefits from exhibiting actual, probability-quantifiable intent” is far the most superior in terms of increased likelihood of being ‘correct’ and, as such, must be given some candidate value raising it above any alternative ‘solution’ that does not.

So, we begin in a state of optimism that if there is a solution to be had, then it must in some way be one that we are — by some means — inevitably guided towards. And this leads on to the question of just how we might go about comparing and evaluating the merits of any and all ‘possible’ solutions we might encounter.

The following (below) is a clip from Episode 11 of Dave Oranchak’s excellent YouTube series Let’s Crack Zodiac. This particular episode, as a whole, treats of the claims made in 2021 by French Engineer Fayçal Ziraoui of having solved both the Z13 and the Z32. As usual, Oranchak expertly walks through these claims and evaluates them against the well-understood difficulties of asserting any such thing in the case of these two very short and problematic ciphers.

The whole episode — in fact the entire series — is well worth a watch if you haven’t already. In the clip here, however, Dave Oranchak is explaining how, for a 2017 television show, he had developed a web tool to visually demonstrate just how many ‘solutions’ to the Z32 are, in theory, possible. Nearly 6,000, in fact, for the presentation.

The question we must now pose, however, is are all these 6,000 possible solutions equally probable, and how might we, in fact, start to filter these down.

(Link)

We’re being tasked with solving a problem posed to us, remember. We’re not a disadvantaged player in some stacked game. Or, if we are, then we should at the very least be honest to ourself and take a step back from the pursuit of mere futility.

Posted by: @shaqmeister

The question we must now pose, however, is are all these 6,000 possible solutions equally probable, and how might we, in fact, start to filter these down.

So, just to first clarify the context, the data we’re going to be looking closer at comprises 58,099 independent possible solves for the Z32. And, what do we mean here by ‘possible’—a term which, all too often, gets mixed up and conflated with much more important words, such as ‘probable’? ‘Possible’, to be clear, is not a relative term. In relation to the entire scope of all things that are possible, no one thing is any more possible than another. There simply aren’t any grades or degrees of possibility. Mere possibility is, in a very real sense, not of any genuine use to us here.

Probability, on the other hand, is a different matter altogether and we shall indeed want to use probability estimates in all and any meaningful evaluations of potential solutions and the like. In fact, this will be a key factor right from the very start in looking to make judgements as to criteria by which we might begin paring down this initially daunting set of 58,099 possible solutions.

Before getting into all that, however, there’s a point that I want to make first, one that I feel is so crucial to everything that follows that I’m just going to state it here without further ado. It is this, that:

You, in attempting to offer a solution to the Z32, are limited by both the cipher length and the presence and specific placing of the three duplicate symbols.

The Zodiac, on the other hand, was not!

This cannot be stressed strongly enough, so step away for a moment to let it start to sink in, if that helps. Again:

You, in your attempt to reconstruct the Z32 plaintext, are under significant constraints as to how you go about it and what you produce.

The Zodiac was completely free to construct it however he pleased.

If the Zodiac had needed an extra couple letters of plaintext to easily and straightforwardly set out his encoded bomb location, then we would now be attempting to solve the Z34, and that’s all there is to it. If we, in our attempt at fitting plausible text into the given 32 character space, are finding ourselves having to compress words, or reorder sentences awkwardly, then we should come right back to what is written above and think again.

And, right from the start, we’re going to let this important reminder stay in the forefront of our thinking as we now begin the process of filtering.

Firstly, then, there is no reasonable meaning to a bearing taken from a mountain and intended to be set out on a map of undoubted inexactness being given to us in milliradians. This is particularly the case when the offered proposals comprise vanishingly small angles with fractional parts to boot, and we can just reject these.

Of course, any rejection of this nature is, in some degree, a subjective decision. So, not to worry. If we’re running out of plausible alternatives later, we can always come back to what we have jettisoned and haul it back in. Only, millirads — or their near equivalent, Mils — are just for small angles. In fact, the whole purpose of millirads is to leverage the fact that, for very small angles the angle in milliradians and the sine of such angles are indistinguishable. This is of great importance in, say, marksmanship. It is not so in the wider world of finding your way about a map.

Secondly, there’s some convention here that needs to be taken into consideration when it comes to setting out and conveying a bearing and a range. And, more to the point, there’s a logic behind the convention. Basically, it is never otherwise than that the bearing precedes the range. Think about it. Before we can set out from any spot we have to first decide what direction we’re going in. I can turn myself to face thirty degrees from North and then start pacing out a hundred yards in that direction. I cannot, however, start pacing in no particular direction whatsoever and then start thinking about which way I ought to be going afterwards.

So, all possible solutions from the set that have the range preceding the bearing are, likewise, rejected. We are now, from just these first two steps, down from 58,099 too 32,223.

Thirdly, then, to conventions having to do with the different idioms that pervade how we speak and how we write. Unless I am to be convinced by evidence I’m currently not aware of, I can only conclude that while we — both in the US and the UK — will use “oh” for “zero” in certain contexts in speech, we simply never write ‘ZERO’ as ‘OH’.

Likewise — and this comes back to the point made at the start — if the Zodiac is intending to give us an angle in radians and a distance in inches then, as the highest probability, we are likely to expect to see ‘RADIANS’ and ‘INCHES’ in the plaintext of his code. Even — remember — if that means that we are having to solve a Z37. Of course, on the other hand, there are valid and accepted abbreviations for both — ‘RAD’ and ‘IN’ — and we might see these with high probability also. What we won’t expect to see, however, is the angle unit as ‘RADIANS’ and the distance unit as ‘IN’. Or, the other way round. So, all inconsistencies of this nature are taken as a fourth criterion for exclusion.

And this same, essentially, goes for the interchangeable words ‘POINT’ and ‘DOT’. It’s one or the other, throughout the plaintext, but not a mixture of both in the same solution. And, at this point, we’re right down to 6,293.

The next is perhaps slightly more subjective, but I see no reason to admit the precedent that the Zodiac is suddenly going to start introducing either symbols, or spaces, into his plaintext, and so possible solves including either ‘&’, ‘+’ or ‘ ’ are left out.

Lastly, then, it comes down to nothing more complicated than rejecting implausible numbers. Taking the magnetic declination around Mount Diablo in the 1970s to be +17 degrees, six radians falls just about directly due North, and we will not see any angles more than a third of a radian greater than this. Trailing and redundant zeros are likewise rejected, as are other oddities such as forming a post-decimal as if it were an integer. (.85 is “point eight five,” not “point eighty-five”.)

So, what are we left with after all this reduction, having set out with a heart-stopping 58,099 ‘possible’ solutions? Actually, the following only — a mere 31 in number — and even some of these pose elements that would appear open to question.

01. THREERADIANTHREEPOINTFIVETWOINCH
02. THREERADIANTHREEPOINTFOURTWOINCH
03. THREERADIANTHREEPOINTNINETWOINCH
04. THREERADIANTHREEPOINTZEROTWOINCH
05. THREERADIANZEROPOINTEIGHTTWOINCH
06. THREERADIANZEROPOINTSEVENTWOINCH
07. THREERADIANZEROPOINTTHREETWOINCH
08. THREEDOTONERADIANDOTEIGHTTWOINCH
09. THREEDOTONERADIANDOTSEVENTWOINCH
10. THREEDOTONERADIANDOTTHREETWOINCH
11. THREEDOTONERADIANEIGHTTENTHSINCH
12. THREEDOTONERADIANFIVEEIGHTHSINCH
13. THREEDOTONERADIANTHREEDOTTWOINCH
14. THREEDOTONERADIANTHREEFIFTHSINCH
15. THREEDOTONERADIANTHREETENTHSINCH
16. THREEDOTTWORADIANDOTEIGHTTWOINCH
17. THREEDOTTWORADIANDOTSEVENTWOINCH
18. THREEDOTTWORADIANDOTTHREETWOINCH
19. THREEDOTTWORADIANEIGHTTENTHSINCH
20. THREEDOTTWORADIANFIVEEIGHTHSINCH
21. THREEDOTTWORADIANTHREEDOTTWOINCH
22. THREEDOTTWORADIANTHREEFIFTHSINCH
23. THREEDOTTWORADIANTHREETENTHSINCH
24. THREEDOTSIXRADIANDOTEIGHTTWOINCH
25. THREEDOTSIXRADIANDOTSEVENTWOINCH
26. THREEDOTSIXRADIANDOTTHREETWOINCH
27. THREEDOTSIXRADIANEIGHTTENTHSINCH
28. THREEDOTSIXRADIANFIVEEIGHTHSINCH
29. THREEDOTSIXRADIANTHREEDOTTWOINCH
30. THREEDOTSIXRADIANTHREEFIFTHSINCH
31. THREEDOTSIXRADIANTHREETENTHSINCH

Collectively, as to bearing, all 31 are directed somewhere between 3 and 3.6 radians from magnetic north. Seven use ‘POINT’ for the decimal divider, the remainder the (to me) somewhat weaker and less compelling ‘DOT’. All, however, convey the same weakness that they give the distance unit — even for a non-unity distance — as ‘INCH’ rather than ‘INCHES’, and this only because I have accepted the same for the angle as ‘RADIAN’ instead of (where appropriate) ‘RADIANS’. And of course, had I not done so, we would in fact be looking at an empty set of candidates at this point. The last ten yet jar on the ear, missing the easy ‘OFAN’ before the final ‘INCH’, as do 11., 12., 14., 15., 19. and 20. Reject these and we’re left with a paltry 15 candidates only.

So, not at all the only result possible through a process of considered pruning, and one you may not — wholly or in part — agree with. Still, as an illustrative example it has served its purpose, which was in the main to demonstrate the power of thinking beyond what is just ‘possible’ to some evaluation of what’s ‘probable’.

And that, in a nutshell, is the primary difference between the pure cryptanalytic approach that can be — and has been — applied with resounding success to the first two longer ciphers, the 408 and the 340. Although a process of relative weighing is internally involved in the act of ‘hill-climbing’ during computer-aided cryptanalysis, the result — possible only given a sufficient unicity — is essentially that this is the only valid solution possible. Here, in attempting an attack on the woefully short Z32, unicity is not our friend and therefore we need something more.

It is this precise ‘something more’ that we should now be setting out to look for.

So, what are we able to learn from this particular exercise?

Let’s start by asking the question why it is that, out of all the initial 58,099 cryptanalytically ‘possible’ solutions, the resultant set has reduced down to only those that give a bearing starting with the digit ‘THREE’? Likewise, why does it appear that we have been compelled in this manner to end the plaintext with the awkward and ill-fitting ‘INCH’ where ‘INCHES’ would have been more to our expectations?

As it happens, these two results are interconnected and the reason is of the highest significant to re-formulating further useful approaches at seeking a stand-out solution to the Z32.

The repeating open triangle at position 2 and 32 of the cipher is the culprit here, and I would hold that the very choice of this repeat specifically is highly likely to have been intentional. I say this for just the very reason that, together with the external (contextual) limitations we must impose on what we are expecting to find in the plaintext — a bearing and a range, at the very least — the additional constraints imposed by just this one select repeat become severe.

If we are committed to radians for the unit angle, and assuming a plaintext that is completed by some combined bearing and range alone, then the very start of the plaintext can only comprise one of ‘ZERO’, ‘ONE’, ‘TWO’, ‘THREE’, ‘FOUR’, ‘FIVE’ and ‘SIX’. (If we are wishing to include a sub-unit angle in the first radian beyond magnetic north and wish to drop the ‘ZERO’, we might want to add ‘POINT’ and ‘DOT’ to these.) But of course, none of these provides the necessary second letter ‘S’ that we would have to have to permit ‘INCHES’ at the very end of the plaintext; and only ‘THREE’ will give us the opportunity to settle for an unsatisfying ‘INCH’ in its place.

Basically, if you want a straight bearing and range in radians and nothing else, then it is going to have to start with ‘THREE’ and end with ‘INCH’. (Note, specifically, that the preceding process of filtering viable results did not, of itself, at any point enforce any such limitation of this kind, and yet the results require it all the same.) And this, to my own personal assessment, is enough to permit me to consider the strong possibility that all 31 of the remaining possible solutions should likewise be rejected and that what we have left of the initial 58,099 is, in fact, the null set.

So, what does this tell us? What are our options now?

Well, we could open up to initially dropping the implicit requirement here that the angle be measured in radians. That, in its turn, would permit consideration of angles in degrees, among other considerations, of which the scope of options for the word at the start is in turn extended. Yet still, not even this attempt will offer up a viable starting choice word with a second letter ‘S’.

So, what else can we consider?

Well, it would seem to me that we are strongly led towards having to drop the second implicit assumption in the data considered here — that the plaintext contains a specification of a bearing and a range and nothing else.

Of course, at this point we are forced to remember that the cipher we are dealing with is very short. The consequence of dropping this contextual assumption, therefore, must be that there will only be room now to give a relatively low-precision bearing and range such that, over all eventualities, it is near impossible to see how these two values can thus retain significant decimal or fractional parts. Is that, then, a problem?

Not necessarily.

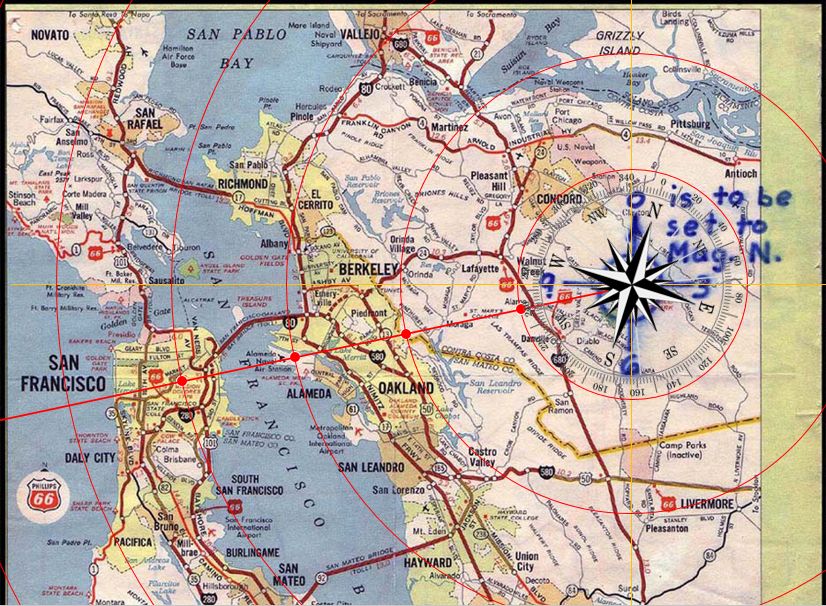
We only have to look again, and more closely, at the map that we’ve been given to realise that all that it really is able to, and does, present are the distinctions between land and water, the major cities and townships, the primary features of the relevant road infrastructure and the locations of where you can get your Phillips gas. Beyond this, there is really nothing further of detail to point to at all. So why would we need precision in our bearing and range anyway?

Basically, if we make the highly reasonable assumption that the bearing/range pair is only intended to point out a very general location of the map — say, nothing more precise than at the level of the city or township — and that the space we have therefore gained in the Z32 plaintext is intended specifically to give whatever detail is required to identify a precise location or feature in that general area, then the primary intention of providing us with information sufficient to locate a bomb somewhere on the map is widened in its possibilities. ‘INCHES’ is pulled back from the end of the cipher, and we are no longer limited to a bearing that must start with ‘THREE’.

So, at this point it would appear that we have turned full circle and have arrived back at the beginning again, having effectively failed to retain any concrete candidate solutions after a considered attempt at pruning down an initially very large data set. We need, therefore, to set out again with something different, and that difference will be this (as has been indicated already):

We are going be attempting to develop a new and hopefully non-empty set of candidates upon first dropping only the implicit constraint of the original data set, that the specification in some form of the expected bearing and range must necessarily take up all the space available within the 32-character cipher.

Basically, then, this will entail again defining a specific format for what will be accepted as a clean and plausible bearing/range pair, without concern at this point whether there is text space left over.

For the actual format, the following will be used to provide an acceptable specification. It will be as:

[#][‘RADIAN(S)’][‘AND’;‘PLUS’;‘’][#][‘INCH(ES)’]

Where decimal parts or fractions are permitted, the decimal point will be rendered only as ‘POINT’. Essentially, we are only going to be accepting complete words for all units and for the number separator. Both ‘ZEROPOINT’ and just ‘POINT’ will be permitted to start angles less that one whole radian.

Of course, this might again appear too extreme and unnecessarily reductive. However, there are good reasons for this and ones that should not be new at this point.

Recall, an overriding premise that has coloured everything that has gone before now is the idea that we’re solving a problem that has been posed under the expectation that we shall succeed. For this reason, at the very least, we have to conclude that its solution must involve — perhaps multi-level — constraints that permit a unique solution to rise, in some manner, above all the others. The actual internal constraints posed by the Z32 are, in contrast, rather minimal. Three pairs of repeating cipher symbols over a cipher text of length 32 is not much of a constraint, if this was all we have.

But, of course, it is not all we have. Alongside the internal constraints we also have a body of external constraints to supplement the former. Some are contextual — we know, in essence, what the nature of the plaintext will be. Yet, it must appear that there remains scope for requiring even further help, and the best position to take on this at the outset is to look for it in every corner imaginable.

Thus, in support of a cipher text with very few duplicate characters, we get the most help if that cipher text is limited to fewer, and longer, words. The duplicates that we do have then become more meaningful, more powerful as constraints. Indeed, from the very sparse spread of them, it has to be at least considered that this scarcity is, in fact, intentionally matched to the needs of the sought plaintext.

Also, we’re merely holding on to the critical point that was raised previously — that the Zodiac, having had the freedom to make his cipher as long as he liked, was not himself compelled in any way to begin arbitrarily introducing contractions and abbreviations.

What, then, do we find.

Well, as it happens, the results that I have obtained from a hopefully complete study of the problem thus posed came as somewhat of a surprise.

Taking the format as above and requiring a clean and direct text giving, from the beginning, both the bearing then the range, the candidate set corresponding to angles measured in radians again came up as the empty set. Effectively, permitting integer as well as fractional values for the angle up to two decimal places, whilst allowing any of ‘AND’, ‘PLUS’ or nothing at all to separate the two coordinates, there were no combinations according to these constraints that could complete without getting tripped up on some or other required letter.

Not. A. One.

Posted by: @shaqmeister

[#][‘RADIAN(S)’][‘AND’;‘PLUS’;‘’][#][‘INCH(ES)’]

Taking the format as above and requiring a clean and direct text giving, from the beginning, both the bearing then the range, the candidate set corresponding to angles measured in radians again came up as the empty set. Effectively, permitting integer as well as fractional values for the angle up to two decimal places, whilst allowing any of ‘AND’, ‘PLUS’ or nothing at all to separate the two coordinates, there were no combinations according to these constraints that could complete without getting tripped up on some or other required letter.

Here’s the breakdown.

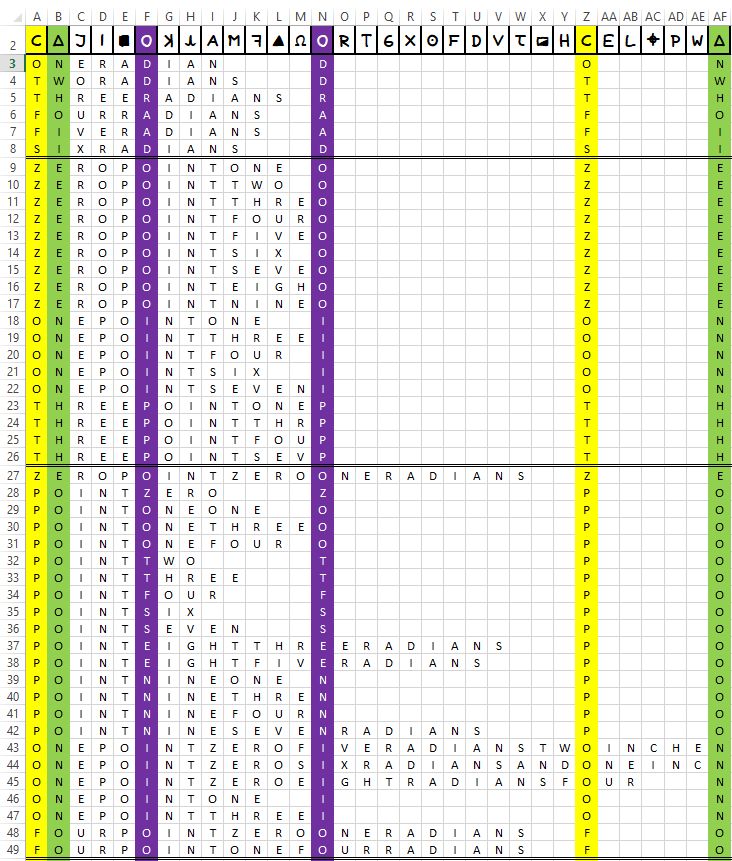
The first block (lines 3–8) give the attempts at fitting any one of the six integer radian bearings. As can be seen these, of necessity, fix one of either ‘R’, ‘A’ or ‘D’ for the first ‘O’ (ciphertext) and, of course, require the same for the second. This, of itself, is actually quite limiting as there are no alphabetised digits in the full range {0,9} that contain the letters ‘A’ or ‘D’. ‘R’ is found in both ‘ZERO’ and ‘FOUR’, but only row 5 is requiring the ‘R’ — at the second ‘O’ — and there are not enough spaces preceding it to permit a fit. The conjunctive ‘AND’ has both ‘A’ and ‘D’, of course. However, there are none among the six alternatives that have these falling in the correct place. ‘PLUS’ is completely excluded here. Hence there are no candidates corresponding to a integer radian bearing matching the required format.

There is, of course, some redundancy evident in presenting all six of the available integer bearings, and such redundancy—where present—will be made use of in what follows. ‘TWO’ and ‘SIX’ can immediately be deemed to fail on the failure of ‘ONE’ in this instance, with all comprising three letters and no one attempt making it past the second ‘O’ to where the first and second duplicates become pertinent to any exclusion. Likewise, ‘FIVE’ fails without further consideration at the failure of ‘FOUR’ (four letters).

On to the second block, then, and here we are looking at bearings expressed to one decimal place using ‘POINT’. For the first time, of course, ‘ZERO’ comes into play. Bearings commencing ‘POINT’ are considered permitted but are not included in this second section as they are covered in the one following and, in that place, are excluded at both precisions.

Here, then, the three possible plaintext letters corresponding to the ciphertext ‘O’ are now ‘O’, ‘I’ and ‘P’. As is shown to be required, however, none of these match around the end of any of the longer numbers ‘THREE’, ‘SEVEN’ nor ‘EIGHT’, and neither do they appear early in a subsequent ‘RADIAN(S)’.

In the third block, at two decimal place precision, all the alternatives beginning ‘POINTZERO’ can be excluded by row 28, which would require a second ‘Z’ to follow at some point that matches no alternatives. The potential candidates that appear to start out well by making it past the second ciphertext ‘O’ either fail at one or other of the last two hurdles, or even overshoot (as in row 44). ‘THREERADIANS…’ to two decimal places in the third block can be ignored as no alternatives could make it past the second ciphertext ‘O’, according to row 5, to progress any further.

And that’s it, unless I have completely missed something, and thus for the second time we find ourselves back at the empty candidate set.

Posted by: @shaqmeister

And that’s it, unless I have completely missed something, and thus for the second time we find ourselves back at the empty candidate set.

So, how is it that we must progress from here?

Well, in essence we must choose either of two paths at this point. We must either 1.) give up on our commitment thus far to only admitting clean language without contractions or abbreviations, or 2.) break with the implicit assumption to this point that the bearing must be given in units of radians.

The first, at this point, would appear premature in the absence of having first explored all the possibilities under the second, and so we will now move on to considering alternative angular units and trial first (yes, there are further alternatives to consider) ‘DEGREES’.

Compared to radians, the scope of integer values available in degrees is greatly increased — to a total 359 possible integer values, as compared to just 6. For this reason, it appears reasonable to limit the scope of candidate angles just to this set of unit values. This would be consistent with the likely accuracy obtained in taking a bearing with a compass in the field. It also sits easily with the imprecise and sparsely marked out (as to precise locations) Phillips map that we have been given. The scale for distances will not change, and we shall continue to accept fractional parts of inches.

As a further point of note, before getting in to it, another sense in which angles in degrees differ from those in radians is that, for any angle over, say, ninety degrees, the expanded written form consistent with our rejection of contractions will of necessity be lengthy even before getting to the range. We shall see how that effects the resultant candidate set.

Here, then, is the comparable breakdown for degrees and inches.

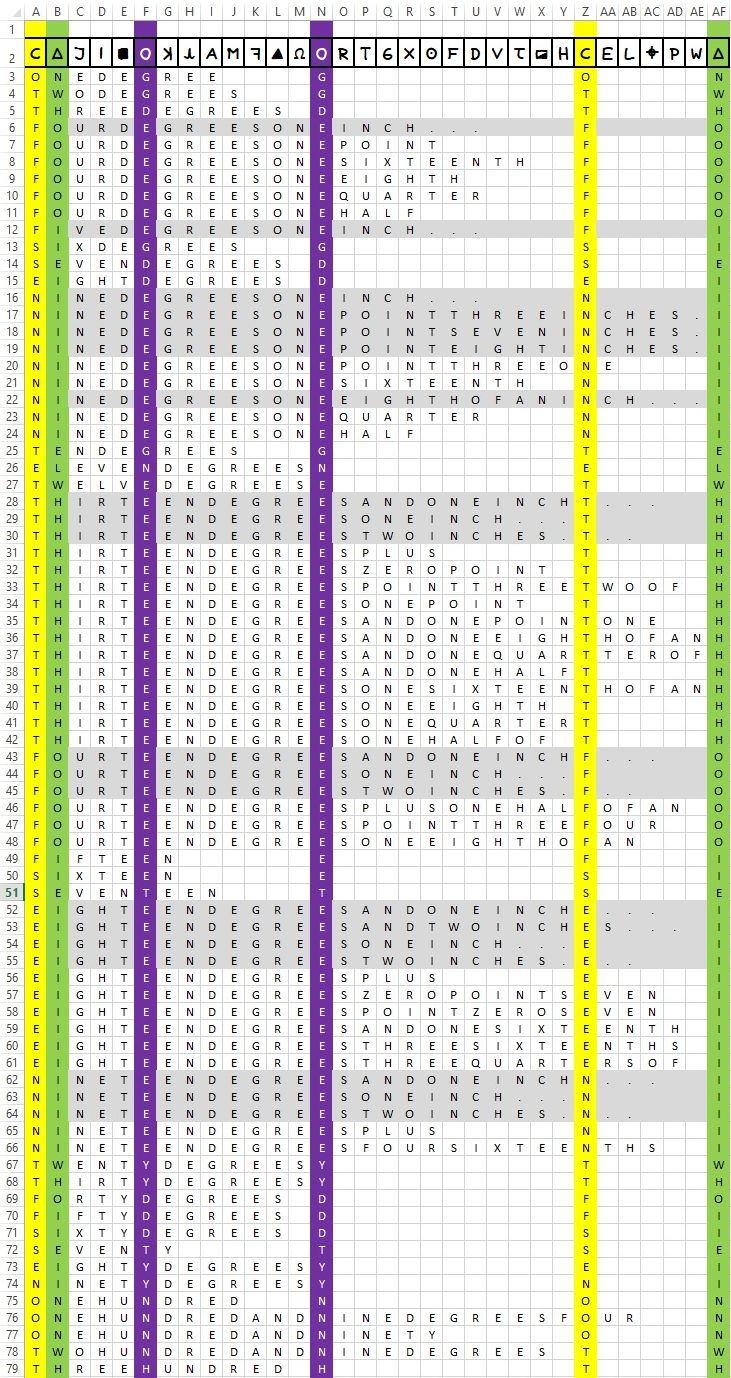
Finally, then, we are producing at least some candidate partial solutions for angles in degrees; twenty to be precise, as below.

01. FOURDEGREESONEINCH.......F.....O
02. FIVEDEGREESONEINCH.......F.....I
03. NINEDEGREESONEINCH.......N.....I
04. NINEDEGREESONEPOINTTHREEINCHES.I
05. NINEDEGREESONEPOINTSEVENINCHES.I
06. NINEDEGREESONEPOINTEIGHTINCHES.I
07. NINEDEGREESONEEIGHTHOFANINCH...I
08. THIRTEENDEGREESANDONEINCHT.....H
09. THIRTEENDEGREESONEINCH...T.....H
10. THIRTEENDEGREESTWOINCHES.T.....H
11. FOURTEENDEGREESANDONEINCHF.....O
12. FOURTEENDEGREESONEINCH...F.....O
13. FOURTEENDEGREESTWOINCHES.F.....O
14. EIGHTEENDEGREESANDONEINCHE.....I
15. EIGHTEENDEGREESANDTWOINCHES....I
16. EIGHTEENDEGREESONEINCH...E.....I
17. EIGHTEENDEGREESTWOINCHES.E.....I
18. NINETEENDEGREESANDONEINCHN.....I
19. NINETEENDEGREESONEINCH...N.....I
20. NINETEENDEGREESTWOINCHES.N.....I

So, why then is it that we are all of a sudden able to generate twenty valid candidates from ‘DEGREES’ where we could not previously generate any from ‘RADIANS’? Does this, in any way whatsoever, indicate that the sought after unique solution thereby must have some elevated probability of matching one of these partial candidate solutions?

In fact, the answer to this question must be no, and for the following reason.

Unlike ‘RADIANS’, which we found in the main generated awkward encodings for the duplicated cipher symbol ‘O’—ones that were very likely to fail against subsequent words for numerical digits—just the simple and merely incidental fact that ‘DEGREE’ is fifty percent made up of ‘E’s will make random hits more likely whenever one of the ‘E’s lands against the ‘O’. Couple this with the fact that we are also, now, getting numbers such as ‘NINETEEN’ for the angle with a cache of ‘E’s of their own, and it’s easy to see that we’re going to be getting a relatively high proportion of matches regardless. Indeed, this lexical advantage is in fact a short-lived one, and is lost entirely once we have reached only ‘TWENTY’ as the start of the plaintext. There is, therefore, nothing in itself here to suggest that the correct solution is more likely to be one of these beyond the mere fact that, at the very least, we no longer have the empty set to work with.

Another similar, and important, point to make is the following.

When undertaking the process of excluding possible candidates that did not match the given starting criteria, one in particular caused hesitation upon its exclusion for the reason that it nonetheless was the only instance found where the plaintext was not partially, but fully, completed. This came out as:

THIRTEENDEGREESANDONEQUARTERINCH

This was rejected, despite being in some sense plausible in terms of clean English language usage, on the basis that it was assessed as comprising a contraction of ‘ONEQUARTEROFANINCH’. Similar exclusions were applied at points during the evaluation using ‘RADIANS’, thus the same was applied here to ensure consistency. However, it was wondered initially whether this risked losing the one candidate that did, in fact, complete the cipher.

It was remembered that an overarching principle of the whole pursuit here is to search for some set of constraints that are, in some way, sufficient to force only one potential candidate solution to stand out as unique. Surely, then, if only one candidate in this evaluation, and one alone, matches a reasonable constraint of effecting completeness, is that not just in the very nature of the kind of criteria we are looking for?

I would argue, again, not.

We have found this one slightly misbehaving candidate to be unique in the sense noted, but that is only because we are in the process of undertaking a comprehensive analysis of a hopefully complete set of viable candidates. It would be unreasonable to suppose that the Zodiac would have done the same. We can hardly imagine him having composed his cipher with such a solution and then spent the time, as we have done here, evaluating all alternatives and adjusting his key until he could be certain of this particular flavour of uniqueness. That is why I have, ultimately, not hesitated to consistently apply the running criteria for exclusion and have this, as a possible candidate, gone.

Posted by: @shaqmeister

The first, at this point, would appear premature in the absence of having first explored all the possibilities under the second, and so we will now move on to considering alternative angular units and trial first (yes, there are further alternatives to consider) ‘DEGREES’.

What, then, of these “further alternatives,” and why don’t we just stop here? We have considered both of the primary and commonly encountered units for angles — degrees and radians — so what else is there to do?

In answer to this — specifically as to why it would be erroneous to quit at having evaluated just degrees and radians — I offer the following.

There is a clear and intentional numbering around the ‘compass rose’ drawn by the Zodiac on the Phillips map, for which it is not possible to give any account under either degrees or radians. Effectively, this numbering divides the full circle into twelfth parts, each of the equivalent of thirty degrees and starting with zero at the top. Having acknowledged as much, then, it would be a dereliction merely to propose that these numbers must have been added for some independent and unknown reason, and not to first take them into consideration as of themselves defining the angular units used. For completeness, and in aid of not being subsequently accused of having overlooked all valid and viable alternatives, we will therefore give the same consideration as we have to both degrees and radians to these ‘twelfth parts’.

Two interpretations for a division of the circle into twelfths appear viable in some degree, and we shall give consideration to both.

Contextually considered, we can note that a twelfth part of the zodiacal circle is a ‘SIGN’ and, in the context of the study of angles around the celestial zodiac a sign is indeed a specific extension of the sexagesimal system for angles — degrees, minutes and seconds of arc — to group angles of thirty degrees. We shall therefore consider signs with some justification.

Equally, but less of an easy fit, we should consider ‘HOUR’. This is somewhat problematic as the underlying model on this interpretation — the clockface — is not, in fact, accurately reflected in the numbering around the Diablo rose, which has ‘0’ at the top rather than ‘12’. We shall evaluate hours, all the same, and also one or more variations on clockface numbering.

For now, let’s start by giving the (hopefully comprehensive) breakdown of potential valid partial candidate solutions that make use of an angle in ‘SIGNS’.

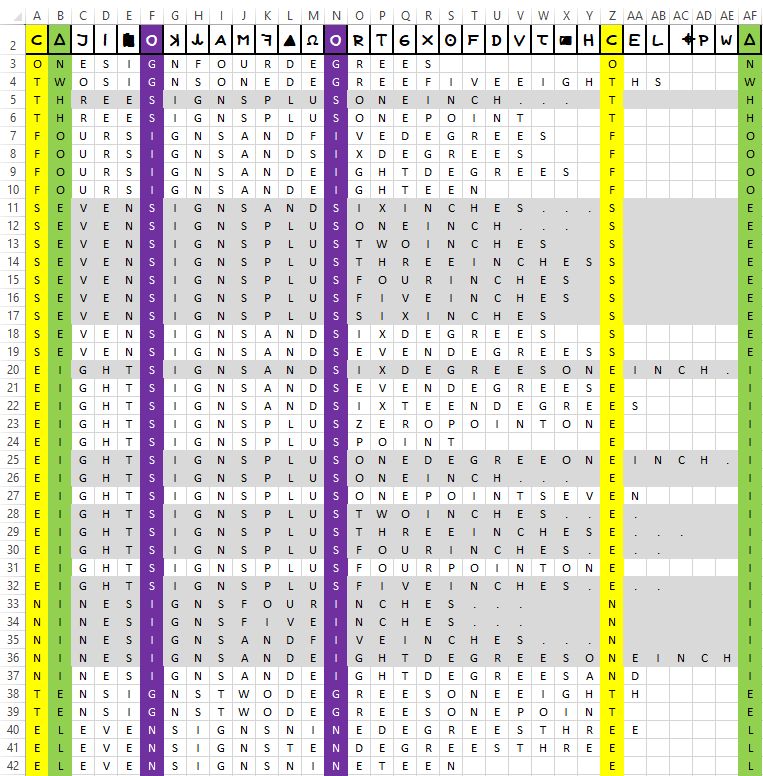
Here then, as in the previous search under ‘DEGREES’, we are able to generate 19 candidate partial solutions for angles in ‘SIGNS’ (below).

01. THREESIGNSPLUSONEINCH....T.....H
02. SEVENSIGNSANDSIXINCHES...S.....E
03. SEVENSIGNSPLUSONEINCH....S.....E
04. SEVENSIGNSPLUSTWOINCHES..S.....E
05. SEVENSIGNSPLUSTHREEINCHESS.....E
06. SEVENSIGNSPLUSFOURINCHES.S.....E
07. SEVENSIGNSPLUSFIVEINCHES.S.....E
08. SEVENSIGNSPLUSSIXINCHES..S.....E
09. EIGHTSIGNSANDSIXDEGREESONEINCH.I
10. EIGHTSIGNSPLUSONEDEGREEONEINCH.I
11. EIGHTSIGNSPLUSONEINCH....E.....I
12. EIGHTSIGNSPLUSTWOINCHES..E.....I
13. EIGHTSIGNSPLUSTHREEINCHESE.....I
14. EIGHTSIGNSPLUSFOURINCHES.E.....I
15. EIGHTSIGNSPLUSFIVEINCHES.E.....I
16. NINESIGNSFOURINCHES......N.....I
17. NINESIGNSFIVEINCHES......N.....I
18. NINESIGNSANDFIVEINCHES...N.....I
19. NINESIGNSANDEIGHTDEGREESONEINCHI 

Note that here, as is consistent with the extended sexagesimal system, we do not consider ‘POINT’ anywhere in the specification of the angle. Where part signs are available, these are conventionally expressed by stepping down to the next unit level, so to speak, with subsequent addition of parts in degrees. Three instances of this form have made it through the candidate selection process at 09., 10. and 19.

Something else that stands out here also is a feature in the results that has not been encountered previously. For the set of candidate values starting with an integer digit of five letters — ‘THREE’, ‘SEVEN’ and ‘EIGHT’ — the combination of the unit, ‘SIGNS’ and the conjunctive, ‘PLUS’, is completely bounded by the two instances of the ciphertext symbol ‘O’. The consequence of this is then that specification of any subsequent integer range in inches is thereby completely unconstrained through the lack of any further duplicated cipher symbol for the next 11 characters following the second ‘O’ (ciphertext). The only partial, but external, constraint is the distances in inches that are made available for any angle given the bounds of the Phillips map. This is, then, a serious feature that may have to be taken into further consideration at some point to come. We put it aside for the present, however, and press on with the final potential ‘unit’ for defining the angle—‘HOURS’.

Posted by: @shaqmeister

We put it aside for the present, however, and press on with the final potential ‘unit’ for defining the angle—‘HOURS’.

Two distinct but nonetheless related attacks are going to be made here. The first will develop candidates using ‘[#]HOURS’ simply. The second will allow for the possibility of a direction according to the ‘[#]OCLOCK’ scheme. Neither are wholly satisfactory, if only for the reason stated that they are both inconsistent with the conventional ‘clockface’ model they are purported to portray in that they require 12 as north (or front-facing), whereas we are given a scale starting with zero.

There are further issues, also, which mar the analogy of using time divisions to represent an angle. We don’t usually pay direct attention to our awareness of the fact, but the clockface itself actually functions through use of what I will call a ‘palimpsest’ of scales — one on top of another, on top of another. One scale for seconds, over one scale for minutes over one scale for hours, all around the one single face. Then, of course, each separate scale requires its own hand to mark it, and three hands at most define three separate directions, and we are only concerned with a single direction. It is, therefore, my contention that the analogy is stretched too far in proposing that the one hand—the hour hand—be permitted to also define subparts of an hour, and consequently only the unit hours will be considered in what follows.

This latter is also consistent with the use of the ‘o’clock’ system whereby, on a ship, “bandit at 8 o’clock” gives immediate meaning, and it would only be introducing confusion in an urgent situation to cry “bandit at 8 o’clock and 27 minutes.”

The following, then, evidences the process of exclusion from assuming ‘HOURS’ as the unit representing angles from north:

which results in the following small candidate set of partial solutions:

01. FOURHOURSPLUSONEINCH.....F.....O
02. FIVEHOURSANDFOURINCHES...F.....I
03. FIVEHOURSPLUSONEINCH.....F.....I
04. SIXHOURSANDFOURINCHES....S.....I
05. NINEHOURSANDFOURINCHES...N.....I
06. NINEHOURSPLUSONEINCH.....N.....I
07. TENHOURSANDFOURINCHES....T.....E
08. TWELVEHOURSONEINCH.......T.....W

whilst for the final set we have:

resulting in a further four*:

01. SEVENOCLOCKTWOINCHES.....S.....E
02. EIGHTOCLOCKTWOINCHES.....E.....I
03. ELEVENOCLOCKANDONEINCH...E.....L
04. ELEVENOCLOCKONEINCH......E.....L

(EDIT: *For some reason, a further one surviving candidate under the last set was missed, or otherwise omitted in error, requiring that we add:

05. ELEVENOCLOCKANDTWOINCHES.E.....L

Its omission here, however does not affect the ultimate result of this study overall.)

In summary…

The method we have been following thus far has been, in all senses, a simple and direct one. At the very outset, we have merely accepted that we have either been presented in the Z32 with a sufficiently constrained problem that is capable of producing a uniquely defined solution, or we are wasting our time if we believe otherwise. In this spirit, then, we have reasonably acknowledged that, alongside the internal constraints of the cipher text as given — length, 32; 3 (only) duplicate cipher symbols — there must be, and are, other external constraints that are far from trivial and that we can leverage in seeking to apply mere exclusion to hopefully get down to a sufficiently limited candidate solution set at the very least.

We know that the code gives the location of a bomb, and we can deduce easily that it will contain in some form a bearing/range pair of coordinates. Although we can be certain that the units of the range will be in inches, as per the scale on the map that we have been given, it has been important to keep open all possibilities as to how the angle is specified.

Continuing the requirement for constraints, however, it has been assumed entirely reasonable to require the text of the cipher to be easily readable, using complete words and not contractions or abbreviations, and that these limitations are logically supported in the awareness that the Zodiac, himself, was not limited to a 32-character cipher and thus, had he needed to avoid contractions, he could have just made it longer. Further, from the same standpoint of requiring constraints, it has to be accepted that any intention of permitting even acknowledged and otherwise valid abbreviations — such as ‘RAD’ for ‘RADIAN’ or ‘IN’ for ‘INCH’ — immediately throws us onto a slippery slope at the bottom of which we will find ourselves devoid of any meaningful constraints whatsoever, and we’re thereby back merely to the futility position that we have already rejected.

The one final supposition has been that, where the cipher is permitted to encode information beyond just the specification of a bearing and range pair, this extra information will come at the end.

And from just this, and hopefully barring any glaring errors or omissions along the way, it has been possible to arrive at a candidate set of just 51* partial solutions to put forward for further study. These are:

01. FOURDEGREESONEINCH.......F.....O
02. FIVEDEGREESONEINCH.......F.....I
03. NINEDEGREESONEINCH.......N.....I
04. NINEDEGREESONEPOINTTHREEINCHES.I
05. NINEDEGREESONEPOINTSEVENINCHES.I
06. NINEDEGREESONEPOINTEIGHTINCHES.I
07. NINEDEGREESONEEIGHTHOFANINCH...I
08. THIRTEENDEGREESANDONEINCHT.....H
09. THIRTEENDEGREESONEINCH...T.....H
10. THIRTEENDEGREESTWOINCHES.T.....H
11. FOURTEENDEGREESANDONEINCHF.....O
12. FOURTEENDEGREESONEINCH...F.....O
13. FOURTEENDEGREESTWOINCHES.F.....O
14. EIGHTEENDEGREESANDONEINCHE.....I
15. EIGHTEENDEGREESANDTWOINCHES....I
16. EIGHTEENDEGREESONEINCH...E.....I
17. EIGHTEENDEGREESTWOINCHES.E.....I
18. NINETEENDEGREESANDONEINCHN.....I
19. NINETEENDEGREESONEINCH...N.....I
20. NINETEENDEGREESTWOINCHES.N.....I
21. THREESIGNSPLUSONEINCH....T.....H
22. SEVENSIGNSANDSIXINCHES...S.....E
23. SEVENSIGNSPLUSONEINCH....S.....E
24. SEVENSIGNSPLUSTWOINCHES..S.....E
25. SEVENSIGNSPLUSTHREEINCHESS.....E
26. SEVENSIGNSPLUSFOURINCHES.S.....E
27. SEVENSIGNSPLUSFIVEINCHES.S.....E
28. SEVENSIGNSPLUSSIXINCHES..S.....E
29. EIGHTSIGNSANDSIXDEGREESONEINCH.I
30. EIGHTSIGNSPLUSONEDEGREEONEINCH.I
31. EIGHTSIGNSPLUSONEINCH....E.....I
32. EIGHTSIGNSPLUSTWOINCHES..E.....I
33. EIGHTSIGNSPLUSTHREEINCHESE.....I
34. EIGHTSIGNSPLUSFOURINCHES.E.....I
35. EIGHTSIGNSPLUSFIVEINCHES.E.....I
36. NINESIGNSFOURINCHES......N.....I
37. NINESIGNSFIVEINCHES......N.....I
38. NINESIGNSANDFIVEINCHES...N.....I
39. NINESIGNSANDEIGHTDEGREESONEINCHI
40. FOURHOURSPLUSONEINCH.....F.....O
41. FIVEHOURSANDFOURINCHES...F.....I
42. FIVEHOURSPLUSONEINCH.....F.....I
43. SIXHOURSANDFOURINCHES....S.....I
44. NINEHOURSANDFOURINCHES...N.....I
45. NINEHOURSPLUSONEINCH.....N.....I
46. TENHOURSANDFOURINCHES....T.....E
47. TWELVEHOURSONEINCH.......T.....W
48. SEVENOCLOCKTWOINCHES.....S.....E
49. EIGHTOCLOCKTWOINCHES.....E.....I
50. ELEVENOCLOCKANDONEINCH...E.....L
51. ELEVENOCLOCKONEINCH......E.....L

All potential bearings in units of radians have been excluded (see discussion here). We have now, however, come to the end of our use of both the internal and contextual external constraints and must, therefore, seek something else if we are to hope to progress further.

That said, the implication of the above is that, if the contextual constraints applied as above are not only valid, but correct, then the actual solution to the Z32 will match, in part, one and only one of the above 51 candidates.

It must be with this optimism, then, that we shall attempt to press on with this ‘problem’.

(EDIT: *Actually, this should be 52 candidates. The following was initially omitted during the relevant reduction, above:

52. ELEVENOCLOCKANDTWOINCHES.E.....L

Its omission there does not, however, result in any change as regards the ultimate result of this study.)

Posted by: @shaqmeister

We have now, however, come to the end of our use of both the internal and contextual external constraints and must, therefore, seek something else if we are to hope to progress further.

It is thus, at this point, that we cannot fairly proceed at all without first acknowledging that we are now, of necessity, entering on a whole new territory. Whether we like it or not, it will henceforth be impossible to avoid introducing into our method some or other degree of unavoidable subjectivity. We have, as stated, exhausted the process of merely inferring reasonable constraints arising both internally, as to the form of the ciphertext, and contextually, given what we can know of what the message is intended to convey.

From hereon out we are required to assume, in order that we may continue to suppose that any unique solution is possible, that the Zodiac has given us something further, intentionally, and sufficient to add a final layer of unique constraints to the problem. But, assuming this is the case, how to find it?

Certainly, we must — as ever — avoid anything that is at all random in its essence. If we are to propose that we have been given the final piece of the puzzle, then it must be in some measure obvious, or at least apparent, that this is so. We must avoid any complex interpretation of things that might look like ‘clues’, in this sense, as complexity will always be the enemy of considered constraints and accepting anything at all complex will be merely to set off in entirely the wrong direction.

So, first of all let’s just review for a moment the data set that we have arrived at and that we are going to continue working with.

We have, then, a set of 51 candidate partial solutions to the Z32 cipher which have survived a process of exclusion and which are, in turn, limited to ones that match the internal constraints of the cipher itself and which give a complete specification of a bearing and range pair. In all instances, besides just this, we have for each a length of cipher up to the end which remains incomplete. As stated, we have used up all the constraints we have encountered thus far. That said, we can yet begin by considering, as a heuristic, in what easy and straightforward manner these remainders may yet evidence scope for intentionally introducing further constraint.

One such plausible possibility arises from the necessity, in each, of having the very last letter of the candidate plaintext given. In all instances, the very last letter of the plaintext is one of ‘O’, ‘I’, ‘H’, ‘E’, ‘W’ or ‘L’. Now from these, and in the absence of having been provided with anything else more specific to help us solve for the ending of the plaintext — either internally or contextually — it would appear entirely reasonable to suggest that this last letter, of itself, is to be chosen so as to add, at least in part, to the additional constraints that we are seeking.

According to this proposal, then, it has to be noted that, for a plaintext in the English language, the most constraining final letter from among these would be the ‘I’. After that might come the ‘O’, and then possibly the ‘H’.

And, in support of a proposal to perhaps consider this one ending above (or at least prior to) the others, we only have to remember how the Zodiac was made aware, right after the Hardens’ early solution to the Z408, that in a real sense it was the ‘I’ that provided the lead in. Harden had made it publicly known that his first assumption was that the Zodiac would be arrogant and would start his coded message with ‘I’.

Here, we again notice that the symbol the Zodiac uses at the end of the Z32 is the ‘open triangle’, which was indeed one of the symbols that he used to encode ‘I’ in the 408. (In the 340 ‘open triangle’ encodes ‘N’, which does not occur at the end of any candidate in the current set.) Further, if we would look at the three remaining symbols from the 408 that were used likewise to encode ‘I’, two of which are present in the 32 ciphertext — viz. reverse-‘K’ and ‘P’ — we see that both were used also to encode ‘I’ in the Z340. So, it is perhaps to be considered as in some degree indicated that we might accept the same for the 32, upon which we then look at how the candidate list might pare down were we to propose an encoding on ‘I’ for each of the three-out-of-four symbols with this same encoding in the 408. And what we get is as in the list below:

01. EIGHTSIGNSPLUSONEINCH....E.....I
02. EIGHTSIGNSPLUSTWOINCHES..E.....I
03. EIGHTSIGNSPLUSTHREEINCHESE.....I
04. EIGHTSIGNSPLUSFOURINCHES.E.....I
05. EIGHTSIGNSPLUSFIVEINCHES.E.....I

Just by taking this one step, if in any sense plausibly justified, the complete candidate set reduces down to just five, all of which sit along a bearing of 8 signs from magnetic north.

Indeed, if we plot these over the Phillips map, we see that we can further drop the last one as 5 inches from Mount Diablo in this direction does not make landfall.

What is more, we have also gained an extra letter third from the last in each remaining candidate, and now have a very tightly constrained ending to boot. The set is now:

01. EIGHTSIGNSPLUSONEINCH....E...I.I
02. EIGHTSIGNSPLUSTWOINCHES..E...I.I
03. EIGHTSIGNSPLUSTHREEINCHESE...I.I
04. EIGHTSIGNSPLUSFOURINCHES.E...I.I

Interestingly, it may be recalled — and if not, see at the end of the previous post here — that when these and a number of other related candidates were first proposed, concern was expressed at the time that their form was such that their specification of the range was all but fully unconstrained and, therefore, that they might become potentially problematic if ultimately retained. This was a concern which arose specifically through noting that these particular candidates were among the only ones for which the combination of the unit and conjunctive — ‘SIGNSPLUS’ — was wholly delimited between the paired and duplicated cipher symbols ‘O’_____‘O’. Now, however, that we are indeed encountering them as the only surviving candidates of a secondary process of exclusion, under the present additional constraints, we find that they have thereby reduced to a set that can now, in fact, be readily subject to distinction on the basis of new constraints factored into the undeciphered plaintext.

Indeed, what in fact remains at this point must be deemed to be sufficiently delimited and constrained that a simple brute force approach may be considered viable in order to effect expansion and subsequent further reduction to, hopefully, only one unique solution.

At the very least, this must be an effort worth undertaking, and all that is needed is just some help from a simple word solving programme and a little persistence besides.

Posted by: @shaqmeister

Indeed, what in fact remains at this point must be deemed to be sufficiently delimited and constrained that a simple brute force approach may be considered viable in order to effect expansion and subsequent further reduction to, hopefully, only one unique solution.

At the very least, this must be an effort worth undertaking, and all that is needed is just some help from a simple word solving programme and a little persistence besides.

But why should we have to work even this hard, when there is a chance that we have been gifted something else to help us on our way?

Consider, at this point, how the four remaining candidate partial solutions differ.

Fundamentally, in terms of the plaintext that we do have for them, we acknowledge a basis for distinction in that each gives a different integer value for the range in inches. However, perhaps more importantly to our purpose here, this is better stated as saying that each gives a range value that is distinguishable in presenting a different and unique character length. In turn, then, this requires that the text that remains to be decoded in each case is likewise of a unique character length. So this, of itself, is an identifiable point of distinction that may help us towards pulling out a single one of these candidates from current four.

Let’s focus then, for a moment, on the four incomplete plaintext sections. These are:

01. ....E...I.I
02. ..E...I.I
03. E...I.I
04. .E...I.I

Their lengths, in order, are therefore 11, 9, 7 and 8 characters respectively.

For the moment, we shall merely register these differences and put them to one side. Suppose, indeed, that instead we now introduce a trial of a different sort.

To begin on a new direction, let it be first merely noticed that in the Z13 cipher there are five cipher symbols that are present also in the Z32. In the latter they occur singly, whilst in Z13 we find duplicates on two of them. Suppose then, in the spirit merely of exploration, we trial substituting into the Z13 whatever encodings we may have reached for these common symbols already in the Z32. The implicit rationale here, of course, is simply one of considering it possible that the two ciphers may, in fact, be built around the same key.

Here is what we get for the Z13:

N......S.G.NS

which is consistent across all four surviving candidate partial solutions.

And we can perhaps take this a step further, also.

We recall that we had reduced an initial candidate set down from 51 to just 4 on the reasoned assumption that taking from the Z408 the encoding of the open triangle at the very end of the Z32 as ‘I’, and then applying the same encoding to the remaining two cipher characters which also match ‘I’ — both in the Z408 and the Z340 — could be considered valid in terms of providing an intentionally identifiable second-level constraint facilitating solution. Essentially, at that point where we were clear that we must achieve some extra help or fail, we found a way, à la Harden, to let “the ‘I’s have it.”

Suppose we do the same with the Z13 and suggest that we take the three repeating ‘8-ball’ characters to, likewise, encode ‘I’. We then get, for the 13:

N...I.ISIG.NS

again, consistently from all four candidates.

And this, of itself, would appear very promising indeed. So let’s break it down some.

The first thing that we notice, of course, is that we’ve pretty much reproduced in the Z13 the word used for the unit of angle in the Z32 candidates, ‘SIGNS’. That is, except for the presence of one apparently interloping character between the ‘G’ and the ‘N’. Without letting this dissuade us, however, what is further apparent is that, immediately preceding this partially corrupt ‘SIGNS’, we find a sequence of six characters which evidence matching against the very last 6 letters of the Z32 in a number of significant ways, and at several different levels.

In the first instance, we note from the ciphertext that the first and third letters of these two blocks — in both instances currently unknown — are encoded by the same cipher symbol in both the Z13 and the Z32. On top of this, again in relation to both text blocks equally, we have the requirement that the last and the third-from-last plaintext characters be the same, and in both instances we here have them as ‘I’s.

Perhaps more importantly, however, when we compare the three ‘I’s we have introduced into the Z13 as encoded by the ‘8-ball’ symbol with the encodings at their respective equivalent places in the Z32, we find that they are encoded in the latter precisely by the very three characters that we pulled from the Z408 in the previous step as likewise encoding ‘I’. It is hard to imagine that this could be anything other than intentional.

We must, in consequence, thereby be encouraged to pursue the idea further that the span of 6 letters from 2 to 7 in the plaintext of the Z13 matches the equivalent span covering the last 6 characters in the 32.

Further we can propose that, just as the Z13 minus the five letters of the slightly disfigured ‘SIGNS’ leaves 8 characters remaining, so we should focus from hereon out on just that one of the four candidates remaining for the Z32 which, likewise, is wanting a further 8 characters to complete.

We are therefore plausibly down to just one candidate partial solution for the Z32 left to ultimately solve. Further, we are now required to regard the letter immediately following ‘INCHES’ as, of necessity, being ‘N’, the second of the last string of six being ‘E’.

EIGHTSIGNSPLUSFOURINCHESNE.E.I.I

Posted by: @shaqmeister

We are therefore plausibly down to just one candidate partial solution for the Z32 left to ultimately solve. Further, we are now required to regard the letter immediately following ‘INCHES’ as, of necessity, being ‘N’, the second of the last six being ‘E’.

EIGHTSIGNSPLUSFOURINCHESNE.E.I.I

And here is where we can now leave the pursuit, as we have reached the point of now only being able to duplicate what has already been argued elsewhere in the thread ‘Z13 as Z32 Mk. I’.

There, as will be seen, the mode of attack was fundamentally different to how we have proceeded here. In that thread, the method of attack was to start with leveraging the observations only just included here, as to the potential for certain noted similarities between the Z13 and the Z32 suggesting a common key, and indeed common words.

Here, in contrast, we have set out from a completely different starting point and have progressed by a different method. Essentially, what we have been exploring in this thread is very much a prequel to the former method, pursuing the idea of plausibly limiting down first the set of valid candidate solutions that it would then be required to consider further.

Of course, in doing so, we have proceeded in a manner that, of necessity, must bring the question of confirmation bias squarely into play. At the very least, in having decided to limit the form in which the bearing and range occur in the plaintext, to avoid both contractions and otherwise ill-formed text, we were thereby aware from the very start that the solution from the other thread would be one that must survive the culling.

What we could not, however, be sure of here is just exactly what else would and would not survive besides.

There was certainly no expectation at the outset of this study that not a single candidate formed on angular units in radians would progress through the process of elimination based on the contextual constraints that were fixed upon. There was no way of preempting, either, the result that just this first elimination process should bring the candidate set right down to a helpful mere 51 remaining. It was likewise on reaching the second level of constraint evaluation, whereby it was proposed as indicated that we might try utilising the same encodings for ‘I’ in the Z32 as were found in the Z408. In this instance, again, we must acknowledge that we were certain in advance that the solution obtained elsewhere must survive. Yet the fact that this, amongst only four candidates all sitting on the same bearing of ‘EIGHTSIGNS’, and no others at all made it through was not something that could have been foreseen. There was always the possibility that candidates beginning ‘FIVEPOINT…’, for example, might have progressed just as readily under this latter constraint, and on radians for the unit of angle, had any such instances otherwise survived.

But of course, for the entire method here to be considered as validly pointing towards at least a unique partial candidate solution, we have to propose that the two (somewhat interrelated, through the mere supposition of a shared key) steps involving the fixing of key instances of the letter ‘I’ are something that we can be expected to have been led towards, when considered in the context as we find it. Basically, this must be the case for these additional ‘helpers’ to have been intentional. Unfortunately this, of itself, is not by any means an easy consideration to pin down definitively.

All the same, having noted and accepted as much, the overall conclusion reached within the bounds of this investigation as a whole must appear undeniable. It is that, on the assumption that the plaintext of the Z32 begins with statement of a bearing and range matching some viable, though possibly broad, place on the Phillips map, written in straight, uncompressed English, coupled of itself with the further assumption of a common key for both the Z13 and the Z32, then only a single, unique solution presents itself as meeting these constraints. Likewise, in support of this finding, the common key assumption itself appears strongly grounded and, again, without this it is not obvious by what other means the ultimate set of 51 candidates from the first stage could be reduced.

And it need not be a concern that, as according to the method followed from the outset in this thread, the explicit limitation to “no contractions or abbreviations” resulted in a single solution containing ‘NE’ as intending “north east.” In fact, both encodings here — for the ‘N’ and the ‘E’ — are fully determined without specific effort, on the assumptions as given. Recall also that, without the former limitation, no solution at all would be possible. If it just happens, however, that the Zodiac merely did use expanded wording only for the bearing, but permitted ‘NE’ later on, then we would only be required to acknowledge that we had been lucky in finding it.

More to the point, if genuine weight is given to the intermediate identification, during the process of co-solution of the 13 and the 32 together, of the three ‘8-balls’ in the Z13 as corresponding to, and singling out, the three instances of symbols in the Z32 that encoded ‘I’ in the original cipher, the 408, then it is easy to see that we could step back, actually permit abbreviations and contractions on all relevant candidate units, and still reduce down to only the single completed candidate as here.

However that is, this solution, or no solution, would appear to be the choice we’ve reached.