Yeah, your are right.
Daikon, if you can think of a way to score cycles so that we can separate the true cycles from the false cycles, it would be greatly appreciated.
So far I have used a simple formula to calculate the percentage of ciphertext that is bracketed by the ciphertext that it should be bracketed by. For example, ABABAB = 4/6 = .60. That actually works pretty well to help flush out the symbols that are not in any strong cycles, like the q and the +. I just add up the total score for each symbol, and compare with the total score for all of the other symbols. For example, for symbol 1, score of 1 with 2, 1 with 3, 1 with 4, etc. all added up. The symbols with the lowest total scores don’t cycle well with other symbols.
I use probability scores. For example, ABABAB = 2^6 = 64, whereas ABAB only scores 2^4 = 16. My cycle "hillclimber" can flush out maybe a dozen or so true two-symbol cycles. I think that is pretty good, considering all of the false two symbol cycles.
It’s sort of like panning for gold. You have to get the light material to float to the top and out of the pan so that there are only a few nuggets at the bottom. I can only work with two symbol cycles in any practical way. But that’s o.k. because ABCD includes AB AC AD BC and CD and sometimes I can find all of them together in practice messages.
If you can think of any other way to score the cycles, to study the cycles to determine what Zodiac did besides cyclic homophonic substitution, or to use the positions of the cycle symbols in the message in any useful way, let me know. Thank you in advance for any participation.
Smokie
I think cosine similarity is useful for corroborating cycle candidates. The measurement compares symbols to each other and tries to find symbols that "act" like other symbols. For example, if symbol A tends to be followed (preceded) by the same symbols that symbol B tends to be followed (preceded) by, then there’s a better chance that they stand for the same plain text letter. Basically, you build vectors based on symbol counts and you measure the distances between them (smaller distances mean greater similarity).
The Copiale cipher was cracked in part by identifying homophones using cosine similarity measurements. Here’s the paper that describes the technique: http://stp.lingfil.uu.se/~bea/publ/copiale-11.pdf
The 340 is probably too short for reliable cosine similarity measurements but maybe they are useful when combined with other techniques.
Thanks for the article! It was easy to read and very interesting. I can imagine people in European high society, such as kings and queens, using ciphers to send messages to each other in the 1500’s. I understand about the cosine relationships a little bit. I know what cosine is, but don’t see any triangle relationships with the vectors. But, I took Calculus 30 years ago. Really a very well written article.
I have been having fun with my cycle hillclimber and different ways to score cycles. I shall post some interesting findings a bit later. I made a message with perfect cycles, and tried my cycle hillclimber with the probability and percentages formulas. Surprisingly, the percentage formula performed much better and paired up a whopping 39 symbols. My next attempt will be at including a value that rewards total distance between the first symbol and the last symbol in a cycle.
EDIT: Jarlve, are you out there? I have a new formula for my cycle hillclimber, and with a message with only perfect cycles (no high count 1:1 or whatever), I was able to gather together 43 symbols. And 9 of the 63 symbols are low count 1:1, for B, F, J, K, etc.
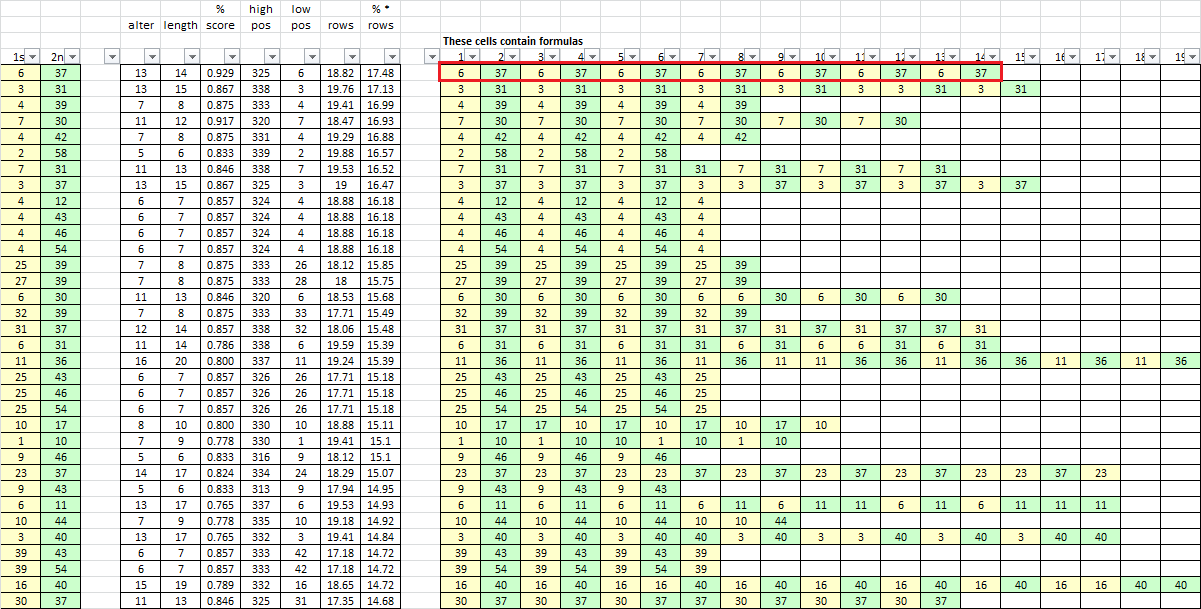
Score = (number of alternations/ count symbol 1 + count symbol 2) * ((high position – low position)/17)
The distance between the high position and low position is figured in total number of rows, so that a cycle that spans from row 1 to row 20 is given higher preference compared to a cycle with the same number of alternations and total count but that starts in say row 2 and ends in row 19. That’s what the 17 is for.
For cycle 1 2 1 2 1 1 1 2 2 in my test message, I get 4 consecutive alternations. Total symbol count is 5 + 4 = 9. High position for the last 2 is 277 and low position for the first 1 is 8. Score = ( 4 / 9 ) * ( 277 – 8 ) / 17 = 7.033.
When I use my cycle hillclimber, only 10 cycle symbols are left standing by themselves without sitting next to a cycle partner. Not all of the cycle symbols are gathered together, so I could get AA in one place, and AA in another place. But the list of possible merges is a lot better with this formula.
Please shoot me a grid of numbers when you can, perfect cycles and that’s all. No other tricks. See if I can identify a lot of the possible merges. I’ll post the graphic of my hillclimber results for the Purple H experiment in a bit so you can see.
Smokie
I understand about the cosine relationships a little bit. I know what cosine is, but don’t see any triangle relationships with the vectors.
It’s a tricky one. Took me a bit to understand what they meant by "cosine relationship" (or "cosine similarity"). I’ll try to explain. They are basically using a dot product. A dot product of two vectors is equal to the cosine of the angle between them. Well, for normalized vectors (i.e. vectors of length 1), otherwise you also need to divide by their lengths. Now it is important to remember that cosine of 0 degrees is 1, cosine of 90 degrees is 0, and cosine of 180 degrees is -1. Another way to look at it: the dot product represents one of the vectors projected onto the other. Sort of like a shadow. If the vectors are perpendicular, the projection (shadow) of either one of them onto the other will be zero. If they are pointing in the same general direction, the projection (shadow) will be the longest.
If you combine all this together, you’ll see that "cosine relationship" is just a number representing whether 2 vectors are pointing in the same general direction (angle is close to 0 degrees, and cosine is 1), or if they are perpendicular (90 degrees, cosine is 0), or if they are pointing in generally opposite directions (180 degrees, cosine is -1). How to calculate the cosine similarity value for two vectors? That’s where the dot product comes in. You just multiply individual coordinates of 2 vectors and add it all together. So if you have to vectors of ( 1, 2, 3, 4, 5) and ( 9, 8, 7, 6, 5 ), their dot product is: 1*9 + 2*8 + 3*7 + 4*6 + 5*5. You’ll also need to divide that number by the length of each of the 2 vectors to normalize it (i.e. bring to -1..1 range). No need to calculate the actual angle, or compute cosines of any angles.
Why does that number tell you whether the vectors are pointing in the same direction, or if they are perpendicular? Magic? Not quite. 🙂 Let’s simplify to 2 dimensions. Let’s make one vector point along X axis: (1,0), and the other along Y axis: (0,1). They are obviously perpendicular to each other (i.e. not at all "similar"). Their dot product is, as expected: 1*0 + 0*1 = 0. Confirmed, they are perpendicular (cosine of 90 degrees is 0). You see, it’s quite simple. Since you are multiplying individual coordinates of the two vectors, if they are "not in sync" with their corresponding coordinates (i.e. one of the coordinates is close to 0 for one of the vectors, but the other one’s isn’t), you end up adding up 0s or very small numbers, which means vectors are mostly perpendicular, or "not similar". However, if both of the vectors have individual coordinates "in sync" (i.e. they are large numbers in both vectors), their dot product will end up close to 1, and these vectors will be "similar".
Going back to ciphers, you take all symbols and count how many times each of them follows (or leads) other symbols. You end up with "vectors" of N numbers representing each symbol (where N is the number of unique symbols in the cipher). Then you can compute dot products between each of the symbols to figure out which ones are "cosine similar" (dot product is close to 1), and those that are grouped together are likely to stand for the same plaintext letter, as they "behave" similarly (i.e. they are likely homophones). The idea is that different letters "like" to follow (or lead) certain other letters (bigram frequencies are not smooth), so it’s like a fingerprint for each letter. And you can group symbols together by their "cosine similarity" fingerprint, as their fingerprints (given a long enough text) will be similar to each other. I haven’t done this test on Z340 myself, but I suspect it might be just too short to get reliable similarity numbers.
You can probably extend this to bigrams, to get an even more accurate result (trigram frequencies are even less smooth). I.e. count how many times a given symbol follows (or leads) a given bigram (a pair of symbols). But you’ll need to have an even longer text for that, so Z340 is definitely out.
If you can think of any other way to score the cycles, to study the cycles to determine what Zodiac did besides cyclic homophonic substitution, or to use the positions of the cycle symbols in the message in any useful way, let me know.
I think it’s a great idea to try to identify cycles and therefore possible candidates for homophones, as it would help reduce the multiplicity of the cipher. In fact, that’s how my "unsolvable" cipher was eventually cracked — by manual analysis of homophone cycles (which I didn’t try to hide at all) and following different possibilities of merging them. But I haven’t done any research in that direction myself, so I can’t really offer any insight, I’m afraid. You definitely seem to have a much better grasp of the cycles.
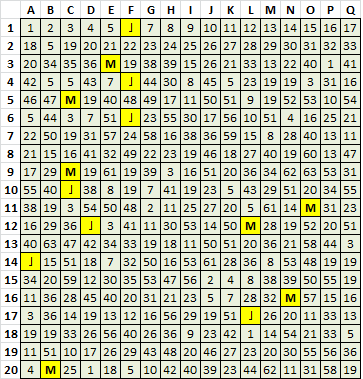
Jarlve, here are my hillclimber results for the Purple H experiment, which is a message with only perfect cycles, no other methods of encryption:
16 20 17 36 12 5 8 1 25 29 26 33 46 9 14 13 24
2 37 42 32 34 12 52 19 43 33 24 39 31 45 47 7 18
4 15 56 51 38 53 60 13 59 44 63 50 1 13 5 26 3
19 55 14 6 40 34 47 24 2 20 39 61 28 35 56 51 11
14 48 22 41 54 24 58 27 40 18 29 13 43 22 8 9 46
53 32 11 45 38 50 59 31 60 58 11 24 16 20 49 36 12
63 44 42 25 5 52 33 46 1 17 57 40 34 4 28 62 47
19 11 56 15 41 55 6 61 13 3 35 13 9 14 30 20 16
48 37 4 57 22 34 26 13 32 54 42 36 16 24 62 49 45
47 13 55 18 29 17 24 41 8 52 39 43 21 53 37 61 51
9 38 59 31 1 19 7 32 49 12 36 40 39 26 50 16 60
33 46 15 56 13 63 44 5 12 36 13 29 54 43 33 16 13
53 35 8 14 48 57 31 24 60 42 44 36 20 17 16 46 63
54 52 25 5 1 12 33 45 34 13 24 29 24 43 58 28 62
47 51 11 56 15 22 55 6 61 59 18 4 26 24 35 37 14
9 30 8 19 24 48 40 21 53 7 57 39 13 60 2 46 62
41 32 34 30 2 12 15 22 45 47 7 13 24 13 55 56 28
61 38 9 51 59 35 13 48 49 17 57 41 62 37 10 20 50
19 39 31 63 5 14 4 15 6 51 32 13 29 44 43 33 36
13 53 24 60 42 54 16 40 49 36 46 63 8 52 25 5 23
The new formula works really well to gather the symbols together!
Daikon: I’ll have to read your last messages after this.
General: The cycle hillclimber is working better now, and gathering cycle symbols together. But it’s only a row of symbols with scores between them, and obviously randomization is going to make things more difficult in the 340. But it’s a start.
Imagine this. Instead of a row of symbols and scores between the symbols, how about a grid of 9*7=63 symbols.
Same approach. The score between symbols 1 and 2 is the two symbol formula score for 1 and 2. Mutate by switching two symbols in the grid and change the scores accordingly. Save higher total scores and keep mutating. A lot of the symbols that are in the same cycles together, even if there is some randomization, should eventually gather together into groups.
Maybe not necessary to make a grid, I don’t know. But it’s a concept. Keep tweaking the formula and using different test messages until you get the best possible formula. Then apply to the 340. Find the best guess as to the cycles and work from there.
Smokie
Hey All-
I had a bit of free time, so I have read over this thread, and also the King/Bahler paper referenced earlier. Does anyone actually have the source code to the "REMOVE_HOMOPHONES" program? I know it was written in Pascal, but I think that converting it to C (or anything better than Pascal) might not be too difficult, and might be useful.
I’ve considered just trying to re-write it in whole from the paper, but I don’t have THAT much free time. ![]()
Also, just trying to help, there are a number of ciphers mentioned in this thread, such as "experiment 1,2,3 etc.," "The mystery cipher," "The Purple H experiment," and so on. I suppose that these ciphers are given somewhere in this long thread, but I could not track them down. Could someone possibly put them in one place, with solutions?
What I mean is that since this is NOT a challenge cipher thread, posting them with solutions is much more helpful, since the idea isn’t to SOLVE them, but to find a method to work out the homophonic cycles. Personally, I just can’t even attempt to help, even if I want to, if I first have to figure out which cipher is which, go find them, then solve then, then FINALLY start to look at cycles. That’s just too much to do in order to try to participate.
I’m not complaining. Good work is being done here. If it were just a bit more organized, others might be able to join in.
-glurk
EDIT: Jarlve, do you think I am wrong in wanting the solutions posted with the ciphers? I think they SHOULD be, since what we are looking for here is cycles or sequences in homophones, and I don’t think anyone will "cheat" on those, or try to make them conform to the given solutions. If a program is able to find them, it won’t matter if the solution is known or unknown.
——————————–
I don’t believe in monsters.
I believe these are the ciphers smokie uses but I don’t know exactly which is what. I included the actual plaintext under the symbolic version every time, they are from my plaintext library which can be found under My work (signature link).
p14hs63a24.txt, perfect cycles, 1 symbol is 1:1 substitute:
zL6ZQi1~Vf0'7?#Ko
E]{+BpYSwnE=^GlN
&fIQ%G‚gMk6@l$J1w
G#)c=(2%=/0R97T=
‚D.?^K5vl+:ownr3|
pNzYLGZ{]IMV~(2=R
c6:l/SC&1im0'^€.3
gkG7!KzQr+p=J=$@?
#ND]oCS=|nl‚)9QvV
M&RT6@f1%G$g.=i0
r:=37w~=#Dz=%=‚n
]LKY{?w+2=ZpfN='
V=$=lkoB=|G&RS/i=
:lZ.M/%€rGQ#YIlZc
('V/?k6~&E=391|^G
)Tzf0wL=m7]{ovgI
R=.r€iK@Yc+‚9p%NB
:TM'LlV{Sv&63I1k0
=zcG.D7=]9lRGrQ$K
?E:fo+!lnp#3w~@NV
thecoreyswereoneo
fthefewoldfamilie
swholingeredinbel
linghamplacetheha
ndsomequietoldstr
eetwhichthesympat
heticobservermust
grievetoseeabando
nedtoboardinghous
esthedwellingsare
statelyandtalland
thewholeplacewear
sanairofaristocra
ticseclusionwhich
mrscoreysfathermi
ghtwellhavethough
tassuredwhenhelef
therhishousethere
athisdeathitisone
oftwoevidentlydes
p70chs63.txt, perfect cycles, 4 symbols are 1:1 substitutes:
p70chs63.txt ----------------- Symbols: 63 Characters: 340 Multiplicity: 0.1852941 Index of Coincidence: 0.0174735 ----------------- Numbered by appearance: 1: [: 6 2: V: 7 3: K: 6 4: ]: 5 5: E: 6 6: X: 6 7: k: 6 8: ;: 6 9: ,: 6 10: n: 6 11: H: 3 12: R: 5 13: i: 6 14: x: 5 15: (: 6 16: ^: 8 17: m: 6 18: : 11 19: B: 4 20: ": 5 21: w: 4 22: p: 6 23: v: 5 24: S: 5 25: }: 6 26: s: 4 27: /: 5 28: ‚: 5 29: Y: 12 30: F: 6 31: D: 5 32: q: 5 33: $: 5 34: b: 23 35: o: 6 36: |: 6 37: =: 5 38: ƒ: 5 39: g: 6 40: l: 5 41: &: 4 42: _: 5 43: -: 6 44: u: 6 45: G: 2 46: 9: 6 47: M: 6 48: a: 2 49: ': 5 50: 1: 3 51: *: 5 52: :: 6 53: Q: 5 54: ~: 2 55: .: 5 56: 4: 3 57: 2: 5 58: T: 1 59: U: 5 60: @: 2 61: t: 3 62: +: 2 63: y: 3 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 16 20 21 22 23 24 25 26 11 27 28 29 30 31 32 33 34 35 36 37 38 39 34 40 34 41 42 43 44 21 12 45 14 46 47 48 16 49 34 50 51 52 53 54 55 8 56 9 18 22 57 36 6 15 1 16 25 18 20 58 44 10 34 59 47 34 30 2 53 13 4 60 23 32 31 29 38 1 43 3 57 5 35 29 34 59 4 16 39 55 61 33 40 52 41 34 27 29 9 10 42 2 7 49 17 37 22 46 34 51 23 15 8 12 29 30 18 56 62 36 6 44 45 34 18 47 25 32 40 43 53 55 18 9 57 22 35 42 38 24 13 36 29 52 28 34 49 14 29 3 39 26 18 44 50 51 15 34 30 2 47 20 27 34 61 46 21 53 54 31 29 55 1 32 43 9 60 37 5 63 22 7 19 17 33 6 10 40 34 25 36 24 35 34 42 52 44 8 12 39 16 46 47 6 26 14 25 63 11 13 20 59 28 18 41 16 27 56 31 49 33 23 51 2 53 29 3 18 18 34 50 15 43 55 38 52 5 4 7 35 30 34 48 37 12 39 19 62 17 18 24 46 29 9 32 34 40 2 14 1 29 43 28 34 10 3 29 42 20 6 63 5 23 57 34 21 22 8 7 49 34 13 38 17 59 34 25 19 36 24 27 51 52 41 31 37 44 61 28 15 47 8 3 35 26 5 33 13 1 2 7 4 17 39 10 16 57 59 34 46 30 [VK]EXk;,nHRix(^m B^"wpvS}sH/‚YFDq $bo|=ƒgblb&_-uwRG x9Ma^'b1*:Q~.;4, p2|X([^}"TunbUMb FVQi]@vqDYƒ[-K2Eo YbU]^g.t$l:&b/Y,n _Vk'm=p9b*v(;RYF 4+|XuGbM}ql-Q., 2po_ƒSi|Y:‚b'xYKg su1*(bFVM"/bt9wQ ~DY.[q-,@=EypkBm$ Xnlb}|Sob_:u;Rg^9 MXsx}yHi"U‚&^/4D '$v*VQYK\b1(-.ƒ: E]koFba=RgB+mS9Y ,qblVx[Y-‚bnKY_"X yEv2bwp;k'biƒmUb} B|S/*:&D=ut‚(M;Ko sE$i[Vk]mgn^2Ub9F shamanarespiritua lguidesandpractit ionersnotofthediv inebutoftheveryel ementsunlikesomeo thermysticsshaman communewithforces thatarenotstrictl ybenevolenttheele mentsarechaotican dlefttotheirownde vicestheyrageagai nstoneanotherinun endingprimalfuryi tisthecallofthesh amantobringbalanc etothischaosactin gasmoderatorsamon gearthfirewateran dairshamansummont
p70chs63_version2.txt, perfect cycles, 4 symbols are 1:1 substitutes:
p70chs63.txt
-----------------
Symbols: 63
Characters: 340
Multiplicity: 0.1852941
Sum of non-repeats: 4387
Index of coincidence: 0.0217074
-----------------
Symbols numbered by order of appearance:
-----------------
1 = Y (c=5)
2 = a (c=4)
3 = c (c=12)
4 = U (c=4)
5 = y (c=11)
6 = F (c=10)
7 = ' (c=11)
8 = p (c=4)
9 = S (c=14)
10 = w (c=5)
11 = C (c=2)
12 = E (c=5)
13 = - (c=4)
14 = k (c=5)
15 = V (c=7)
16 = " (c=8)
17 = m (c=11)
18 = o (c=4)
19 = 1 (c=5)
20 = Z (c=3)
21 = 8 (c=13)
22 = I (c=4)
23 = J (c=10)
24 = N (c=3)
25 = b (c=1)
26 = = (c=4)
27 = n (c=12)
28 = M (c=6)
29 = s (c=5)
30 = _ (c=6)
31 = 4 (c=5)
32 = e (c=23)
33 = u (c=10)
34 = * (c=13)
35 = L (c=4)
36 = q (c=4)
37 = z (c=6)
38 = (c=4)
39 = ! (c=6)
40 = : (c=3)
41 = 6 (c=2)
42 = 0 (c=2)
43 = & (c=2)
44 = 3 (c=6)
45 = . (c=3)
46 = > (c=3)
47 = A (c=2)
48 = ; (c=3)
49 = 2 (c=3)
50 = , (c=4)
51 = v (c=4)
52 = / (c=1)
53 = W (c=4)
54 = + (c=3)
55 = Q (c=3)
56 = 5 (c=3)
57 = r (c=2)
58 = @ (c=3)
59 = ) (c=2)
60 = O (c=3)
61 = ^ (c=2)
62 = R (c=1)
63 = B (c=3)
-----------------
Symbolic cipher:
-----------------
YacUyF'pSwCE-kV"c
mo"1Z8IyJNb='nMs_
4eu*LqFeze!:S6E0
kJ8&"3e.V>*AS;28m
*,SuMv"Fm1/8YeW*e
_+SQ5rwzsnIq@cUyJ
ne,W"u8)4!Oepn*v
3a'Vc-SFeMY_=Enzm
2^8J*0emSu!3:8*mS
58FVwyL*n>'eMkncJ
ZmS._ze!+81;eRuN*
AsnSI3@8rQyB*'oc4
FqVeJSyueMO8pEF"J
*u6kFBC-1U'm"=2s
_4vzaSncmme.!:8Y>
y,'J3e&LEuo^cmyFn
*VeM+kwn@'eIcn_1J
ByqWeZS;'zeQvc5eu
o8yp!Os-*)'3S=cF
Ny4LYa'UcJw",WeuV
shamanarespiritua
lguidesandpractit
ionersnotofthediv
inebutoftheveryel
ementsunlikesomeo
thermysticsshaman
communewithforces
thatarenotstrictl
ybenevolenttheele
mentsarechaotican
dlefttotheirownde
vicestheyrageagai
nstoneanotherinun
endingprimalfuryi
tisthecallofthesh
amantobringbalanc
etothischaosactin
gasmoderatorsamon
gearthfirewateran
dairshamansummont
-----------------
Nummeric cipher:
-----------------
1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,3
17,18,16,19,20,21,22,5,23,24,25,26,7,27,28,29,30
31,32,33,34,35,36,6,32,37,32,38,39,40,9,41,12,42
14,23,21,43,16,44,32,45,15,46,34,47,9,48,49,21,17
34,50,9,33,28,51,16,6,17,19,52,21,1,32,53,34,32
30,54,9,55,56,57,10,37,29,27,22,36,58,3,4,5,23
27,32,50,53,16,33,21,59,31,39,60,38,32,8,27,34,51
44,2,7,15,3,13,9,6,32,28,1,30,26,12,27,37,17
49,61,21,23,34,42,32,17,9,33,39,44,40,21,34,17,9
56,21,6,15,10,5,35,34,27,46,7,32,28,14,27,3,23
20,17,9,45,30,37,32,39,54,21,19,48,32,62,33,24,34
47,29,27,9,22,44,58,21,57,55,5,63,34,7,18,3,31
6,36,15,32,23,9,5,33,32,28,60,21,8,12,6,16,23
34,33,41,14,6,63,11,13,19,4,7,17,38,16,26,49,29
30,31,51,37,2,9,27,3,17,17,32,45,39,40,21,1,46
5,50,7,23,44,32,43,35,12,33,18,61,3,17,5,6,27
34,15,32,28,54,14,10,27,58,7,32,22,3,27,30,19,23
63,5,36,53,32,20,9,48,7,37,32,55,51,3,56,32,33
18,21,5,8,39,60,38,29,13,34,59,7,44,9,26,3,6
24,5,31,35,1,2,7,4,3,23,10,16,50,53,32,33,15
-----------------
Nummeric cipher for ZKDecrypto:
-----------------
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 3
17 18 16 19 20 21 22 5 23 24 25 26 7 27 28 29 30
31 32 33 34 35 36 6 32 37 32 38 39 40 9 41 12 42
14 23 21 43 16 44 32 45 15 46 34 47 9 48 49 21 17
34 50 9 33 28 51 16 6 17 19 52 21 1 32 53 34 32
30 54 9 55 56 57 10 37 29 27 22 36 58 3 4 5 23
27 32 50 53 16 33 21 59 31 39 60 38 32 8 27 34 51
44 2 7 15 3 13 9 6 32 28 1 30 26 12 27 37 17
49 61 21 23 34 42 32 17 9 33 39 44 40 21 34 17 9
56 21 6 15 10 5 35 34 27 46 7 32 28 14 27 3 23
20 17 9 45 30 37 32 39 54 21 19 48 32 62 33 24 34
47 29 27 9 22 44 58 21 57 55 5 63 34 7 18 3 31
6 36 15 32 23 9 5 33 32 28 60 21 8 12 6 16 23
34 33 41 14 6 63 11 13 19 4 7 17 38 16 26 49 29
30 31 51 37 2 9 27 3 17 17 32 45 39 40 21 1 46
5 50 7 23 44 32 43 35 12 33 18 61 3 17 5 6 27
34 15 32 28 54 14 10 27 58 7 32 22 3 27 30 19 23
63 5 36 53 32 20 9 48 7 37 32 55 51 3 56 32 33
18 21 5 8 39 60 38 29 13 34 59 7 44 9 26 3 6
24 5 31 35 1 2 7 4 3 23 10 16 50 53 32 33 15
-----------------
Symbolic cycles:
-----------------
Old symbol: s, homophone(s): YwIqv (YwIqvYwIqvYwIqvYwIqvYw)
Old symbol: h, homophone(s): a:>+@O (a:>+@Oa:>+@Oa:>+@Oa)
Old symbol: a, homophone(s): cy' (cy'cy'cy'cy'cy'cy'cy'cy'cy'cy'cy'c)
Old symbol: m, homophone(s): U,W5 (U,W5U,W5U,W5U,W)
Old symbol: n, homophone(s): FJu (FJuFJuFJuFJuFJuFJuFJuFJuFJuFJu)
Old symbol: r, homophone(s): p-=L;Q (p-=L;Qp-=L;Qp-=L;Qp-=L)
Old symbol: e, homophone(s): S8* (S8*S8*S8*S8*S8*S8*S8*S8*S8*S8*S8*S8*S8*S)
Old symbol: p, homophone(s): Cb (CbC)
Old symbol: i, homophone(s): Ek1s4 (Ek1s4Ek1s4Ek1s4Ek1s4Ek1s4)
Old symbol: t, homophone(s): VM_z!3 (VM_z!3VM_z!3VM_z!3VM_z!3VM_z!3VM_z!3V)
Old symbol: u, homophone(s): " ("""""""")
Old symbol: l, homophone(s): m (mmmmmmmmmmm)
Old symbol: g, homophone(s): oB (oBoBoBo)
Old symbol: d, homophone(s): ZN6 (ZN6ZN6ZN)
Old symbol: c, homophone(s): n (nnnnnnnnnnnn)
Old symbol: o, homophone(s): e (eeeeeeeeeeeeeeeeeeeeeee)
Old symbol: f, homophone(s): . (...)
Old symbol: v, homophone(s): 0A (0A0A)
Old symbol: b, homophone(s): &^ (&^&^)
Old symbol: y, homophone(s): 2r (2r2r2)
Old symbol: k, homophone(s): / (/)
Old symbol: w, homophone(s): )R ()R))
-----------------
Nummeric cycles:
-----------------
Old symbol: s, homophone(s): 1,10,22,36,51 (1,10,22,36,51,1,10,22,36,51,1,10,22,36,51,1,10,22,36,51,1,10)
Old symbol: h, homophone(s): 2,40,46,54,58,60 (2,40,46,54,58,60,2,40,46,54,58,60,2,40,46,54,58,60,2)
Old symbol: a, homophone(s): 3,5,7 (3,5,7,3,5,7,3,5,7,3,5,7,3,5,7,3,5,7,3,5,7,3,5,7,3,5,7,3,5,7,3,5,7,3)
Old symbol: m, homophone(s): 4,50,53,56 (4,50,53,56,4,50,53,56,4,50,53,56,4,50,53)
Old symbol: n, homophone(s): 6,23,33 (6,23,33,6,23,33,6,23,33,6,23,33,6,23,33,6,23,33,6,23,33,6,23,33,6,23,33,6,23,33)
Old symbol: r, homophone(s): 8,13,26,35,48,55 (8,13,26,35,48,55,8,13,26,35,48,55,8,13,26,35,48,55,8,13,26,35)
Old symbol: e, homophone(s): 9,21,34 (9,21,34,9,21,34,9,21,34,9,21,34,9,21,34,9,21,34,9,21,34,9,21,34,9,21,34,9,21,34,9,21,34,9,21,34,9,21,34,9)
Old symbol: p, homophone(s): 11,25 (11,25,11)
Old symbol: i, homophone(s): 12,14,19,29,31 (12,14,19,29,31,12,14,19,29,31,12,14,19,29,31,12,14,19,29,31,12,14,19,29,31)
Old symbol: t, homophone(s): 15,28,30,37,39,44 (15,28,30,37,39,44,15,28,30,37,39,44,15,28,30,37,39,44,15,28,30,37,39,44,15,28,30,37,39,44,15,28,30,37,39,44,15)
Old symbol: u, homophone(s): 16 (16,16,16,16,16,16,16,16)
Old symbol: l, homophone(s): 17 (17,17,17,17,17,17,17,17,17,17,17)
Old symbol: g, homophone(s): 18,63 (18,63,18,63,18,63,18)
Old symbol: d, homophone(s): 20,24,41 (20,24,41,20,24,41,20,24)
Old symbol: c, homophone(s): 27 (27,27,27,27,27,27,27,27,27,27,27,27)
Old symbol: o, homophone(s): 32 (32,32,32,32,32,32,32,32,32,32,32,32,32,32,32,32,32,32,32,32,32,32,32)
Old symbol: f, homophone(s): 38,45 (38,45,38,45,38,45,38)
Old symbol: v, homophone(s): 42,47 (42,47,42,47)
Old symbol: b, homophone(s): 43,61 (43,61,43,61)
Old symbol: y, homophone(s): 49,57 (49,57,49,57,49)
Old symbol: k, homophone(s): 52 (52)
Old symbol: w, homophone(s): 59,62 (59,62,59)
p44mhs63.txt, some randomization in the cycles, some 1:1 substitutes:
p44.txt ----------------- Symbols: 63 Characters: 340 Multiplicity: 0.1852941 Sum of non-repeats: 4175 Index of coincidence: 0.0172479 ----------------- Symbols numbered by order of appearance: ----------------- 1 = k (c=5) 2 = u (c=8) 3 = o (c=5) 4 = , (c=7) 5 = e (c=8) 6 = r (c=5) 7 = 1 (c=6) 8 = F (c=4) 9 = . (c=4) 10 = 7 (c=11) 11 = 3 (c=13) 12 = [ (c=6) 13 = g (c=5) 14 = % (c=3) 15 = t (c=6) 16 = V (c=4) 17 = ^ (c=6) 18 = J (c=12) 19 = R (c=5) 20 = ` (c=5) 21 = v (c=8) 22 = _ (c=6) 23 = > (c=5) 24 = w (c=5) 25 = ! (c=5) 26 = < (c=4) 27 = (c=5) 28 = O (c=8) 29 = X (c=8) 30 = p (c=4) 31 = P (c=8) 32 = @ (c=8) 33 = E (c=9) 34 = T (c=10) 35 = ' (c=4) 36 = N (c=12) 37 = 6 (c=2) 38 = G (c=4) 39 = I (c=6) 40 = - (c=5) 41 = ( (c=4) 42 = h (c=9) 43 = + (c=5) 44 = z (c=10) 45 = Q (c=2) 46 = L (c=5) 47 = : (c=4) 48 = i (c=7) 49 = ; (c=7) 50 = Z (c=1) 51 = U (c=3) 52 = l (c=3) 53 = y (c=3) 54 = q (c=2) 55 = d (c=2) 56 = n (c=4) 57 = # (c=4) 58 = C (c=2) 59 = / (c=3) 60 = Y (c=2) 61 = = (c=1) 62 = ? (c=2) 63 = m (c=1) ----------------- Symbolic cipher: ----------------- kuuo,er1F.73[g%tV ^J^R`v_>,w!<OXpP @E3JTX3[g'N767wvE utGI-(vh.+JzPX<@Q TL:OzoNi`-;7Z71`t TvULh3Ep,kXrVFQ@ E!RNP3z+>T'Ie[Jl` .@yquTGhd%L+n#iu( woIig:Cle^3tEJz_ OrNTP<7#-Jz^pXk/- @VY;7R>_1vN[P3:=P JzwgO!'Nh;J,eL.E nh3GN^XNT1@qh;t[; ?3y+J`/1iU(VikoXC ErRIi;7F!h>,LhevN _<N67nwOY'@GIe3Ed T;J%(E1+uPOJT@go ,73iN7v!e3ruhXv^R I:tPeOzp-#nTz/uU? kJzm_#l3,_yFOz>N[ allthetracesofaff initywithorconsci ousnessofthebeowu lfthatwecandiscov erandtheyareveryf ewaresuchastofavo urthisdatetheonly completeparallelt othefableisfoundi ntheicelandicsaga ofgrettirwhoisaki ndofnorthernhercu lesthisheroperfor msmanygreatfeatsb uttherearethreewh ichbelongtothesup ernaturalinoneoft hesehewrestleswit hafiendcalledglam andkillshimandtho ----------------- Nummeric cipher: ----------------- 1,2,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16 17,18,17,19,20,21,22,23,4,24,25,26,27,28,29,30,31 32,33,11,18,34,29,11,12,13,35,36,10,37,10,24,21,33 2,15,38,39,40,41,21,42,9,43,18,44,31,29,26,32,45 34,46,47,28,44,3,36,48,20,40,49,10,50,10,7,20,15 34,21,51,46,42,11,33,30,4,1,29,6,27,16,8,45,32 33,25,19,36,31,11,44,43,23,34,35,39,5,12,18,52,20 9,32,53,54,2,34,38,42,55,14,46,43,56,57,48,2,41 24,3,39,48,13,47,58,52,5,17,11,15,27,33,18,44,22 28,6,36,34,31,26,10,57,40,18,44,17,30,29,1,59,40 32,16,60,49,10,19,23,22,7,21,36,12,31,11,47,61,31 18,44,24,13,28,27,25,35,36,42,49,18,4,5,46,9,33 56,42,11,38,36,17,29,36,34,7,32,54,42,49,15,12,49 62,11,53,43,18,20,59,7,48,51,41,16,48,1,3,29,58 33,6,19,39,48,49,10,8,25,42,23,4,46,42,5,21,36 22,26,36,37,10,56,24,28,60,35,32,38,39,5,11,33,55 34,49,18,14,41,33,7,43,2,31,28,27,18,34,32,13,3 4,10,11,48,36,10,21,25,5,11,6,2,42,29,21,17,19 39,47,15,31,5,28,44,30,40,57,56,34,44,59,2,51,62 1,18,44,63,22,57,52,11,4,22,53,8,28,44,23,36,12 ----------------- Nummeric cipher for ZKDecrypto: ----------------- 1 2 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 17 19 20 21 22 23 4 24 25 26 27 28 29 30 31 32 33 11 18 34 29 11 12 13 35 36 10 37 10 24 21 33 2 15 38 39 40 41 21 42 9 43 18 44 31 29 26 32 45 34 46 47 28 44 3 36 48 20 40 49 10 50 10 7 20 15 34 21 51 46 42 11 33 30 4 1 29 6 27 16 8 45 32 33 25 19 36 31 11 44 43 23 34 35 39 5 12 18 52 20 9 32 53 54 2 34 38 42 55 14 46 43 56 57 48 2 41 24 3 39 48 13 47 58 52 5 17 11 15 27 33 18 44 22 28 6 36 34 31 26 10 57 40 18 44 17 30 29 1 59 40 32 16 60 49 10 19 23 22 7 21 36 12 31 11 47 61 31 18 44 24 13 28 27 25 35 36 42 49 18 4 5 46 9 33 56 42 11 38 36 17 29 36 34 7 32 54 42 49 15 12 49 62 11 53 43 18 20 59 7 48 51 41 16 48 1 3 29 58 33 6 19 39 48 49 10 8 25 42 23 4 46 42 5 21 36 22 26 36 37 10 56 24 28 60 35 32 38 39 5 11 33 55 34 49 18 14 41 33 7 43 2 31 28 27 18 34 32 13 3 4 10 11 48 36 10 21 25 5 11 6 2 42 29 21 17 19 39 47 15 31 5 28 44 30 40 57 56 34 44 59 2 51 62 1 18 44 63 22 57 52 11 4 22 53 8 28 44 23 36 12 ----------------- Symbolic cycles: ----------------- Old symbol: a, homophone(s): kF%+:-U (kF%-+:-UkF+%+:-k-:+UkF%+:-UkF) Old symbol: l, homophone(s): uln# (uuulun#ul#nnuu#nu#l) Old symbol: t, homophone(s): orR>'G( (orR>'G(orR>'G(orR>'G(orR>'G(orR>) Old symbol: h, homophone(s): ,NI (,,NIN,NIINNN,NNI,NNI,NI,N) Old symbol: e, homophone(s): Ti7he (e7T77hTi77ThTeThiieT77hehThiii7hhe7eTT7i7eheT) Old symbol: r, homophone(s): 1!L; (1!L;1L!L;1!;L1;;1;!L;1!) Old symbol: c, homophone(s): .<p (.<p.<p.<p.<p) Old symbol: s, homophone(s): 3X (3X3X3X3X33X33X3X333X3) Old symbol: o, homophone(s): [w@ ([w@[w@@[@w@[w@[w@@[) Old symbol: f, homophone(s): gtV (gtVgttVgtVgtVgt) Old symbol: i, homophone(s): ^_P (^^_PPP^_P^_PP^_P^P__) Old symbol: n, homophone(s): JO (JOJJOJJOJJOJJOJOJOJO) Old symbol: y, homophone(s): ` (`````) Old symbol: w, homophone(s): v (vvvvvvvv) Old symbol: u, homophone(s): E (EEEEEEEEE) Old symbol: b, homophone(s): 6C (6CC6) Old symbol: d, homophone(s): z (zzzzzzzzzz) Old symbol: v, homophone(s): QZ (QZQ) Old symbol: m, homophone(s): y? (y?y?y) Old symbol: p, homophone(s): qd (qdqd) Old symbol: g, homophone(s): /Y (/Y/Y/) Old symbol: k, homophone(s): =m (=m) ----------------- Nummeric cycles: ----------------- Old symbol: a, homophone(s): 1,8,14,43,47,40,51 (1,8,14,40,43,47,40,51,1,8,43,14,43,47,40,1,40,47,43,51,1,8,14,43,47,40,51,1,8) Old symbol: l, homophone(s): 2,52,56,57 (2,2,2,52,2,56,57,2,52,57,56,56,2,2,57,56,2,57,52) Old symbol: t, homophone(s): 3,6,19,23,35,38,41 (3,6,19,23,35,38,41,3,6,19,23,35,38,41,3,6,19,23,35,38,41,3,6,19,23,35,38,41,3,6,19,23) Old symbol: h, homophone(s): 4,36,39 (4,4,36,39,36,4,36,39,39,36,36,36,4,36,36,39,4,36,36,39,4,36,39,4,36) Old symbol: e, homophone(s): 34,48,10,42,5 (5,10,34,10,10,42,34,48,10,10,34,42,34,5,34,42,48,48,5,34,10,10,42,5,42,34,42,48,48,48,10,42,42,5,10,5,34,34,10,48,10,5,42,5,34) Old symbol: r, homophone(s): 7,25,46,49 (7,25,46,49,7,46,25,46,49,7,25,49,46,7,49,49,7,49,25,46,49,7,25) Old symbol: c, homophone(s): 9,26,30 (9,26,30,9,26,30,9,26,30,9,26,30) Old symbol: s, homophone(s): 11,29 (11,29,11,29,11,29,11,29,11,11,29,11,11,29,11,29,11,11,11,29,11) Old symbol: o, homophone(s): 12,24,27,32 (12,24,27,32,12,24,32,27,32,12,32,24,27,32,12,24,27,32,12,24,32,27,32,12) Old symbol: f, homophone(s): 13,15,16 (13,15,16,13,15,15,16,13,15,16,13,15,16,13,15) Old symbol: i, homophone(s): 17,22,31 (17,17,22,31,31,31,17,22,31,17,22,31,31,17,22,31,17,31,22,22) Old symbol: n, homophone(s): 18,28 (18,28,18,18,28,18,18,28,18,18,28,18,18,28,18,28,18,28,18,28) Old symbol: y, homophone(s): 20 (20,20,20,20,20) Old symbol: w, homophone(s): 21 (21,21,21,21,21,21,21,21) Old symbol: u, homophone(s): 33 (33,33,33,33,33,33,33,33,33) Old symbol: b, homophone(s): 37,58 (37,58,58,37) Old symbol: d, homophone(s): 44 (44,44,44,44,44,44,44,44,44,44) Old symbol: v, homophone(s): 45,50 (45,50,45) Old symbol: m, homophone(s): 53,62 (53,62,53,62,53) Old symbol: p, homophone(s): 54,55 (54,55,54,55) Old symbol: g, homophone(s): 59,60 (59,60,59,60,59) Old symbol: k, homophone(s): 61,63 (61,63)
Wildcard simulation though I’m not 100% sure about plaintext anymore:
=`Y>[Ta1Tj3ZC@Ryk oqB7yRLu7-F?(ONo5 n:dx+VSK7%IgaU4PW 0tX!kFBApu;H3Ed(E :wuj=74+v7w#TSdC7 77?u7PV.z%qeUgSOb `RZSa7`A>dF7][73n LiwKyGvV#5HT=[pXe B%gUk(Hx?]7HFbBVg -ak7IO;d`1w%:AEj+ gqo.Su7PeCFVLVdi@ 0p3dUc+Kt50yN=7cb XKFv4:a]xTEkG>%NH z71`u51Bj(-d!TX77 `VRk?T5b7IcCOoAw7 7v%#:(XO+ZTFSEL0P @kP>g7BNi%WpHYun- .%kdjIbCzd:?7wgt; qdS#PO5GFLzceudPo Twik[ykUXn>VEp%Bv ilikekillingpeopl ebecauseitissomuc hfunitismorefunth ankillingwildgame intheforrestbecau semanisthemostdan gerousanimalofall tokillsomethinggi vesmethemostthril lingexperenceitis evenbetterthanget tingyourrocksoffw ithagirlthebestpa rtofitisthatwheni dieiwillbereborni nparadiceandallth eihavekilledwillb ecomemyslavesiwil lnotgiveyoumyname becauseyouwilltry 1 2 3 4 5 6 7 8 6 9 10 11 12 13 14 15 16 17 18 19 20 15 14 21 22 20 23 24 25 26 27 28 17 29 30 31 32 33 34 35 36 37 20 38 39 40 7 41 42 43 44 45 46 47 48 16 24 19 49 50 22 51 52 10 53 32 26 53 31 54 22 9 1 20 42 34 55 20 54 56 6 36 32 12 20 20 20 25 22 20 43 35 57 58 38 18 59 41 40 36 27 60 2 14 11 36 7 20 2 49 4 32 24 20 61 5 20 10 30 21 62 54 37 15 63 55 35 56 29 52 6 1 5 50 47 59 19 38 40 41 16 26 52 33 25 61 20 52 24 60 19 35 40 23 7 16 20 39 27 51 32 2 8 54 38 31 49 53 9 34 40 18 17 57 36 22 20 43 59 12 24 35 21 35 32 62 13 45 50 10 32 41 64 34 37 46 29 45 15 28 1 20 64 60 47 37 24 55 42 31 7 61 33 6 53 16 63 4 38 28 52 58 20 8 2 22 29 8 19 9 26 23 32 48 6 47 20 20 2 35 14 16 25 6 29 60 20 39 64 12 27 17 49 54 20 20 55 38 56 31 26 47 27 34 11 6 24 36 53 21 45 43 13 16 43 4 40 20 19 28 62 38 44 50 52 3 22 30 23 57 38 16 32 9 39 60 12 58 32 31 25 20 54 40 46 51 18 32 36 56 43 27 29 63 24 21 58 64 59 22 32 43 17 6 54 62 16 5 15 16 41 47 30 4 35 53 50 38 19 55
Mystery cipher before columnar transposition, perfect cycles and a few 1:1 substitutes I believe:
p20.txt ----------------- Symbols: 63 Characters: 340 Multiplicity: 0.1852941 Sum of non-repeats: 6456 Index of coincidence: 0.0190352 ----------------- Symbols numbered by order of appearance: ----------------- 1 = O (c=2) 2 = i (c=5) 3 = L (c=5) 4 = 6 (c=3) 5 = M (c=4) 6 = u (c=12) 7 = a (c=6) 8 = 5 (c=5) 9 = A (c=4) 10 = 1 (c=24) 11 = = (c=6) 12 = - (c=6) 13 = d (c=10) 14 = ; (c=5) 15 = o (c=10) 16 = h (c=5) 17 = [ (c=3) 18 = 8 (c=10) 19 = : (c=6) 20 = z (c=9) 21 = _ (c=3) 22 = K (c=5) 23 = 0 (c=7) 24 = U (c=11) 25 = 4 (c=6) 26 = & (c=4) 27 = (c=4) 28 = H (c=11) 29 = y (c=4) 30 = I (c=2) 31 = Z (c=6) 32 = @ (c=4) 33 = k (c=7) 34 = q (c=7) 35 = > (c=4) 36 = 7 (c=7) 37 = l (c=6) 38 = G (c=6) 39 = b (c=2) 40 = ' (c=6) 41 = ] (c=6) 42 = e (c=2) 43 = Q (c=5) 44 = / (c=4) 45 = 3 (c=4) 46 = S (c=5) 47 = f (c=6) 48 = ! (c=3) 49 = ^ (c=4) 50 = r (c=4) 51 = s (c=2) 52 = < (c=5) 53 = n (c=4) 54 = g (c=4) 55 = Y (c=2) 56 = c (c=4) 57 = t (c=4) 58 = ` (c=4) 59 = % (c=4) 60 = C (c=1) 61 = 9 (c=4) 62 = . (c=4) 63 = + (c=3) ----------------- Symbolic cipher: ----------------- OiL6Mua5A1=-d;oh[ 8:1z_1K0dMAU4&H; yIZ@kq>o7uh8zUl10 dHGb']Ooue8Q/U1k3 zSf!=^-d_rqHeu7s< n:Uag[foLYc510Z48 ;'-lHGt`z1doh8%MS 1ku]qi=@&7KaQUg4 Z:z<>H1^'S%1/dy1C oQ3u;Uc1=h80`Hlt9 r1IZkizfuG&U;>d1 Lq<'.]57/H1+uKaSy 4%10r-koQ6AL!Ulg3 8b=GqH]nz<+_5suat K4%9:U7Hl&GZ0d1^' f`yMcr]iS@-koa.8 4qn617Lu:10=>U11k @Q!9/zfd3o-8h5Hlz <^Z:q.'9doY1.u7`8 A1K[fUGgH]tn+iu1c chaplinalsorememb erselsatellinghim aboutthetimeeinst einconceivedhisth eoryofrelativityd uringbreakfastone morningheseemedlo stinthoughtandign oredhisfoodsheask edhimifsomethingw asbotheringhimhes atdownathispianoa ndstartedplayingh econtinuedplaying andwritingnotesfo rhalfanhourthenwe ntupstairstohisst udywhereheremaine dfortwoweekswithe lsabringinguphisf ----------------- Nummeric cipher: ----------------- 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17 18,19,10,20,21,10,22,23,13,5,9,24,25,26,27,28,14 29,30,31,32,33,34,35,15,36,6,16,18,20,24,37,10,23 13,28,38,39,40,41,1,15,6,42,18,43,44,24,10,33,45 20,46,47,48,11,49,12,13,21,50,34,28,42,6,36,51,52 53,19,24,7,54,17,47,15,3,55,56,8,10,23,31,25,18 14,40,12,37,28,38,57,58,20,10,13,15,16,18,59,5,46 10,33,6,41,34,2,11,32,26,27,36,22,7,43,24,54,25 31,19,20,52,35,28,10,49,40,46,59,10,44,13,29,10,60 15,43,45,6,14,24,56,10,11,16,18,23,58,28,37,57,61 50,10,30,31,33,2,20,47,6,38,26,27,24,14,35,13,10 3,34,52,40,62,41,8,36,44,28,10,63,6,22,7,46,29 25,59,10,23,50,12,33,15,43,4,9,3,48,24,37,54,45 18,39,11,38,34,28,41,53,20,52,63,21,8,51,6,7,57 22,25,59,61,19,24,36,28,37,26,38,31,23,13,10,49,40 47,58,29,5,56,50,41,2,46,32,12,33,27,15,7,62,18 25,34,53,4,10,36,3,6,19,10,23,11,35,24,10,10,33 32,43,48,61,44,20,47,13,45,15,12,18,16,8,28,37,20 52,49,31,19,34,62,40,61,13,15,55,10,62,6,36,58,18 9,10,22,17,47,24,38,54,28,41,57,53,63,2,6,10,56 ----------------- Nummeric cipher for ZKDecrypto: ----------------- 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 10 20 21 10 22 23 13 5 9 24 25 26 27 28 14 29 30 31 32 33 34 35 15 36 6 16 18 20 24 37 10 23 13 28 38 39 40 41 1 15 6 42 18 43 44 24 10 33 45 20 46 47 48 11 49 12 13 21 50 34 28 42 6 36 51 52 53 19 24 7 54 17 47 15 3 55 56 8 10 23 31 25 18 14 40 12 37 28 38 57 58 20 10 13 15 16 18 59 5 46 10 33 6 41 34 2 11 32 26 27 36 22 7 43 24 54 25 31 19 20 52 35 28 10 49 40 46 59 10 44 13 29 10 60 15 43 45 6 14 24 56 10 11 16 18 23 58 28 37 57 61 50 10 30 31 33 2 20 47 6 38 26 27 24 14 35 13 10 3 34 52 40 62 41 8 36 44 28 10 63 6 22 7 46 29 25 59 10 23 50 12 33 15 43 4 9 3 48 24 37 54 45 18 39 11 38 34 28 41 53 20 52 63 21 8 51 6 7 57 22 25 59 61 19 24 36 28 37 26 38 31 23 13 10 49 40 47 58 29 5 56 50 41 2 46 32 12 33 27 15 7 62 18 25 34 53 4 10 36 3 6 19 10 23 11 35 24 10 10 33 32 43 48 61 44 20 47 13 45 15 12 18 16 8 28 37 20 52 49 31 19 34 62 40 61 13 15 55 10 62 6 36 58 18 9 10 22 17 47 24 38 54 28 41 57 53 63 2 6 10 56 ----------------- Symbolic cycles: ----------------- Old symbol: c, homophone(s): Ob (ObOb) Old symbol: h, homophone(s): i>/3` (i>/3`i>/3`i>/3`i>/3`i) Old symbol: a, homophone(s): L5Kyr (L5KyrL5KyrL5KyrL5KyrL5K) Old symbol: p, homophone(s): 6+ (6+6+6+) Old symbol: l, homophone(s): MA_ (MA_MA_MA_MA) Old symbol: i, homophone(s): uUH (uUHuUHuUHuUHuUHuUHuUHuUHuUHuUHuUHu) Old symbol: n, homophone(s): a4lG] (a4lG]a4lG]a4lG]a4lG]a4lG]a4lG]) Old symbol: s, homophone(s): 1 (111111111111111111111111) Old symbol: o, homophone(s): =Z'S (=Z'S=Z'S=Z'S=Z'S=Z'S=Z') Old symbol: r, homophone(s): -:f (-:f-:f-:f-:f-:f-:f) Old symbol: e, homophone(s): do8z (do8zdo8zdo8zdo8zdo8zdo8zdo8zdo8zdo8zdo8) Old symbol: m, homophone(s): ;h (;h;h;h;h;h) Old symbol: b, homophone(s): [I ([I[I[) Old symbol: t, homophone(s): 0kq7 (0kq70kq70kq70kq70kq70kq70kq7) Old symbol: g, homophone(s): > (>>>>) Old symbol: u, homophone(s): @n (@n@n@n@n) Old symbol: v, homophone(s): e (ee) Old symbol: d, homophone(s): Q<% (Q<%Q<%Q<%Q<%Q<) Old symbol: y, homophone(s): !s (!s!s!) Old symbol: f, homophone(s): ^c (^c^c^c^c) Old symbol: k, homophone(s): YC (YCY) Old symbol: w, homophone(s): 9. (9.9.9.9.) ----------------- Nummeric cycles: ----------------- Old symbol: c, homophone(s): 1,39 (1,39,1,39) Old symbol: h, homophone(s): 2,27,35,44,45,58 (2,27,35,44,45,58,2,27,35,44,45,58,2,27,35,44,45,58,2,27,35,44,45,58,2) Old symbol: a, homophone(s): 3,8,22,29,50 (3,8,22,29,50,3,8,22,29,50,3,8,22,29,50,3,8,22,29,50,3,8,22) Old symbol: p, homophone(s): 4,63 (4,63,4,63,4,63) Old symbol: l, homophone(s): 5,9,21 (5,9,21,5,9,21,5,9,21,5,9) Old symbol: i, homophone(s): 6,24,28 (6,24,28,6,24,28,6,24,28,6,24,28,6,24,28,6,24,28,6,24,28,6,24,28,6,24,28,6,24,28,6,24,28,6) Old symbol: n, homophone(s): 7,25,37,38,41 (7,25,37,38,41,7,25,37,38,41,7,25,37,38,41,7,25,37,38,41,7,25,37,38,41,7,25,37,38,41) Old symbol: s, homophone(s): 10 (10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10) Old symbol: o, homophone(s): 11,31,40,46 (11,31,40,46,11,31,40,46,11,31,40,46,11,31,40,46,11,31,40,46,11,31,40) Old symbol: r, homophone(s): 12,19,47 (12,19,47,12,19,47,12,19,47,12,19,47,12,19,47,12,19,47) Old symbol: e, homophone(s): 13,15,18,20 (13,15,18,20,13,15,18,20,13,15,18,20,13,15,18,20,13,15,18,20,13,15,18,20,13,15,18,20,13,15,18,20,13,15,18,20,13,15,18) Old symbol: m, homophone(s): 14,16 (14,16,14,16,14,16,14,16,14,16) Old symbol: b, homophone(s): 17,30 (17,30,17,30,17) Old symbol: t, homophone(s): 23,33,34,36 (23,33,34,36,23,33,34,36,23,33,34,36,23,33,34,36,23,33,34,36,23,33,34,36,23,33,34,36) Old symbol: g, homophone(s): 26,54,57 (26,54,57,26,54,57,26,54,57,26,54,57) Old symbol: u, homophone(s): 32,53 (32,53,32,53,32,53,32,53) Old symbol: v, homophone(s): 42 (42,42) Old symbol: d, homophone(s): 43,52,59 (43,52,59,43,52,59,43,52,59,43,52,59,43,52) Old symbol: y, homophone(s): 48,51 (48,51,48,51,48) Old symbol: f, homophone(s): 49,56 (49,56,49,56,49,56,49,56) Old symbol: k, homophone(s): 55,60 (55,60,55) Old symbol: w, homophone(s): 61,62 (61,62,61,62,61,62,61,62)
Mystery cipher after columnar transposition (I ran into trouble here and had to manually retrace cycles back from the original):
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 3 17 13 26 4 27 28 17 8 29 30 26 19 31 32 33 34 28 35 14 22 36 17 7 37 10 5 38 26 39 4 27 17 40 41 42 22 43 10 34 7 44 45 12 46 10 45 19 47 36 11 48 49 35 27 25 50 4 51 52 51 1 28 17 53 23 37 54 22 9 55 15 16 21 7 26 56 57 33 22 14 3 40 58 27 47 44 4 7 19 8 59 12 17 11 42 43 1 17 34 26 35 21 6 36 18 20 54 30 10 24 17 48 4 39 37 23 31 29 60 27 58 17 40 17 49 19 47 55 10 27 59 7 43 33 3 61 26 22 28 11 57 17 41 14 19 37 3 26 52 17 29 34 17 6 20 24 10 4 51 32 44 15 40 18 10 16 35 1 62 31 42 17 63 39 47 36 48 27 34 28 26 46 21 58 33 52 41 12 13 16 43 54 7 17 2 42 44 50 15 22 38 10 35 57 27 63 25 19 1 53 11 48 36 61 4 28 18 21 17 23 40 26 44 37 33 49 27 58 20 42 8 7 24 51 59 1 55 22 52 12 34 47 62 6 31 30 16 2 26 29 21 35 17 17 34 36 28 11 23 17 10 53 17 51 61 15 14 30 43 27 39 19 19 12 22 41 33 4 46 7 40 23 10 62 48 49 36 35 22 62 56 17 4 59 61 37 7 44 9 6 63 13 17 10 51 55 26 57 53 27 17 54 18 42 homophone(s): 5,38 (5,38,5,38) homophone(s): 6,24,29,43,41,59 (6,24,29,43,41,59,6,24,29,43,41,59,6,24,29,43,41,59,6,24,29,43,41,59,6) homophone(s): 16,15,18,31,52 (16,15,18,31,52,16,15,18,31,52,16,15,18,31,52,16,15,18,31,52,16,15,18) homophone(s): 2,63 (2,63,2,63,2,63) homophone(s): 8,13,25 (8,13,25,8,13,25,8,13,25,8,13) homophone(s): 10,26,27 (10,26,27,10,26,27,10,26,27,10,26,27,10,26,27,10,26,27,10,26,27,10,26,27,10,26,27,10,26,27,10,26,27,10) homophone(s): 1,21,33,38,41 (1,21,33,38,41,1,21,33,38,41,1,21,33,38,41,1,21,33,38,41,1,21,33,38,41,1,21,33,38,41) homophone(s): 17 (17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17) homophone(s): 11,37,40,47 (11,37,40,47,11,37,40,47,11,37,40,47,11,37,40,47,11,37,40,47,11,37,40) homophone(s): 12,23,51 (12,23,51,12,23,51,12,23,51,12,23,51,12,23,51,12,23,51) homophone(s): 4,7,22,19 (4,7,22,19,4,7,22,19,4,7,22,19,4,7,22,19,4,7,22,19,4,7,22,19,4,7,22,19,4,7,22,19,4,7,22,19,4,7,22) homophone(s): 3,14 (3,14,3,14,3,14,3,14,3,14) homophone(s): 9,32 (9,32,9,32,9) homophone(s): 28,34,35,36 (28,34,35,36,28,34,35,36,28,34,35,36,28,34,35,36,28,34,35,36,28,34,35,36,28,34,35,36) homophone(s): 20,54,57 (20,54,57,20,54,57,20,54,57,20,54,57) homophone(s): 30,53 (30,53,30,53,30,53,30,53) homophone(s): 45 (45,45) homophone(s): 43,48,58 (43,48,58,43,48,58,43,48,58,43,48,58,43,48) homophone(s): 46,51 (46,50,46,50,46) homophone(s): 49,55 (49,55,49,55,49,55,49,55) homophone(s): 56,60 (56,60,56) homophone(s): 61,62 (61,62,61,62,61,62,61,62)
I am out there,
smokie, that is a really nice improvement to your system. I see that you reduced the weight of longer cycles, it’s something which we do in the solvers also but in another way. We use the log function on the score of the n-gram. So you could possibly try to keep your exponential system but just encapsulate the score of each cycle in a log10 function.
Try the grid! Experimentation is good.
glurk made some good points and I’m thinking to create an entire new suite of test ciphers (with plaintexts this time) including some of the new stuff I’d like to see tested, what do you think smokie?
Edit: ideally I’d like to start a new thread for the cycle work so that I can consolidate all the test ciphers to start of the thread.
I will clean up my posts to include better references and citation links before I do anything else. The grid idea may come in the future. But I am working with a spreadsheet on a small computer, so that’s a pretty big project. If you want to start a new, better organized thread, that’s fine with me. But I can stay here too. It doesn’t matter to me. Quicktrader started the thread a long time ago and disappeared after making one post. His objective I think was to suggest working on the cycles. This thread is disorganized and includes a lot of my stream of consciousness and redundant summations. If you want to start a new thread and set forth more specific objectives with the first post, that’s fine. I will use my cycle hillclimber or anything else that I have already used according to your rules. Or you can invite others to use their computer programming skills to do something else or whatever you want and we can keep my spreadsheet efforts here. Either way. Part of my objective is to inspire more experienced people than myself.
I like the idea of testing a new set of messages. I am really excited about my cycle hillclimber. I have suspicions that Zodiac may have switched some of the cycles or uses for some of the symbols while encoding. Now that I understand more about probability scoring and have explored the cycles with different formulas, I feel differently about the q and think that it may have some relationship with the < { q q < q q q q < q < q < q < q < q }, with the bold being the double q. Why did he double the q, making it look like the q was not in a cycle, and then later cycle the q with the <? But I stray from the topic and still haven’t fully digested daikon’s post.
I have to go out of town today, but will clean things up for referencing in this thread before I experiment with anything else.
We use the log function on the score of the n-gram. So you could possibly try to keep your exponential system but just encapsulate the score of each cycle in a log10 function.
It’s a good simplification, but there is an actual reason for using logs, it’s not just a heuristic. The table of N-gram frequencies represents the probability of each of them appearing in a given text. So, for example, if you use a table that say that TH bigram appears 1588 times out of a total of 58600 bigrams, that simply means that the probability of finding TH in a given text is 1588 / 58600 = 0.027, or P(‘TH’) = 0.027. In statistics, if you need to compute the probability of two independent events, you simply multiply their probability. So, for example, if you want to find out the probability of bigrams AB and TH both appearing in the same text, you multiply their probabilities (or their frequencies from the bigram table). In math notation: P(‘AB’|’TH’) = P(‘AB’) × P(‘TH’). Now, going back to logarithms, you probably remember that log(A×B) = log(A) + log(B). Conversely, 10^(A+B) = 10^A × 10^B (where 10^A means 10 to the power of A). I.e. when you are working with powers, or exponents, you need to *add* them when you are *multiplying* the whole numbers.
Going back to ciphers, when you are scoring a possible solution using N-gram stats, you are simply computing the probability of the solution text appearing in an English text (a longer one, presumably). If the probability is low (small score), it is less likely to be a coherent English, compared to a higher probability (larger score) solution. To compute the probability of a solution, you need to *multiply* the probabilities of separate N-grams appearing in it. So, for a possible solution ‘ABCCD’, the score is P(‘AB’|’BC’|’CC’|’CD’) = P(‘AB’) × P(‘BC’) × P(‘CC’) × P(‘CD’). The problem is, when you are multiplying very small numbers, you end up with much-much smaller numbers very quickly. For example, if the probability of bigram ZV is 0.0001 (not sure what it is exactly, but it’s definitely a rare one), and you happen to have 3 of them in the solution you are trying to score, you end up with 0.0001 × 0.0001 × 0.0001 = 0.000000000001, or 1e-12. Computers can only represent floating point values as small as 1e-38, I believe, even if you are using double precision floats. So if you try to score a solution with a lot of rare N-grams, you’ll bump into floating point underflow error, when your score will likely dip below the smallest representable floating point value during computations.
One of the possible solutions — use logs of probabilities! Then you need to *add* them, instead of multiplying, so you won’t have issues with underflow errors. Plus, as an added benefit, computers do additions a bit faster than multiplications. And no need to use an expensive exp() function at the end to get the actual probability value, since we will be comparing the scores relative to each other. Which means we are fine with the score equal to log of the probability, and we don’t care about the exact probability value.
Just thought I’ll mention this, as it is a common solution to work with logs when you have to multiple a lot of numbers, that can potentially be small. Which happens a lot when you are working with probabilities.
Glurk, here are some citations for the experiments, which I also included in the text of my posts:
See viewtopic.php?f=81&t=267&start=50, post # 5, p70chs63.txt (this is Experiment 1 J-ST, or "Experiment 1").
See: viewtopic.php?f=81&t=267&start=50, post # 7, p70chs63.txt (this is Experiment 2 J-ST, or "Experiment 2").
See: viewtopic.php?f=81&t=267&start=70, post # 2, p44.txt (this is Experiment 3 J-ST, or "Experiment 3").
See: viewtopic.php?f=81&t=267&start=80, post # 5, and viewtopic.php?f=81&t=267&start=90, post # 1 (this is the "Mystery Cipher").
Thanks for the interest. Smokie
O.k. guys, this may be a bit premature, but we can always take these results off of the table and start anew.
I ran the 340 with my new scoring system. These are the first few lines, sorted by score. Score = (# of alternations/ total symbol count) * number of rows spanned.
Keeping things very simple (and leaving out symbol 30 for right now, which also cycles imperfectly with 6 and 37), I just want to ask what you guys think about the top result, with 6 and 37, which are the backwards L and the M.
6 count = 7
37 count = 7
And three other symbols in the message have a total count of 7 (if that matters):
21 count = 7
31 count = 7
50 count = 7
1. What is the probability of this being a Zodiac made cycle and not a random cycle? Can we merge them together into one symbol? Why or why not?
2. Considering the start position of 6 and end position of 325, is there any way to use plaintext frequencies to guess at what plaintext 6 and 37 map to, with the hypothetical assumption that there are no other symbols in the cycle?
Smokie
Smokie-
Can you test your Excel program against this numeric cipher?:
792 839 777 106 523 761 459 858 34 357 997 149 523 623 153 243 634 20 764 758 106 523 784 938 152 839 777 858 792 357 107 727 34 106 523 55 858 459 777 938 727 422 792 152 106 925 727 839 795 107 727 963 523 761 459 997 422 607 634 623 795 925 758 997 243 141 634 784 107 963 152 795 761 839 997 761 764 607 153 34 149 963 634 353 607 55 623 858 422 20 357 795 149 149 243 149 963 761 758 925 764 149 107 459 422 727 34 399 106 152 399 839 523 607 925 963 459 997 107 727 784 422 357 353 353 273 623 634 758 858 243 761 106 764 784 925 34 149 623 602 777 357 353 795 152 141 141 243 758 858 764 34 997 938 784 938 623 149 607 634 357 938 106 243 758 107 761 963 153 607 353 141 784 858 422 764 523 925 963 795 938 141 727 34 107 727 623 106 422 727 357 925 997 758 107 607 839 634 458 858
This is the EXACT cipher mentioned above in the King/Bahler paper (Table 2) which I OCR’d and corrected. It is completely sequential, and the homophones are known and are listed in the paper. The plaintext is:
FOURSCOREANDSEVENYEARSAGOOURFATHERSBROUG HTFORTHONTHISCONTINENTANEWNATIONCONCEIVE DINLIBERTYANDDEDICATEDTOTHEPROPOSITIONTH ATALLMENARECREATEDEQUALNOWWEAREENGAGEDIN AGREATCIVILWARTESTINGWHETHERTHATNATIONOR
-glurk
——————————–
I don’t believe in monsters.