I wanted to explore the search space of all possible replacements for the "+" symbol, under the assumption that the "+" symbol is meant to be a wildcard and can be replaced by any other symbol in the 340’s alphabet.

To measure the appearance of non-random "interesting things", I have the following four scores:

1) Average probability of the 25 least probable repeated ngrams or fragments.
2) Average cosine similarity of the 25 most similar symbol pairs
3) Average probability of the 25 least probable repeated homophone cycle candidates, L=2
4) Jarlve’s measurement of non-repeats

The search tries to minimize each measurement, so the cosine similarity is subtracted from 1 (so very similar pairs of symbols approach 0), and Jarlve’s non-repeat measurement is subtracted from 10000 (so it gets smaller as more nonrepeats are found)

The search is currently limited to the "+" symbol, just to keep things simple. It is a multiobjective hillclimbing search, meaning it explores a "surface" of solutions that are "pareto optimal" (that is, no solution within the surface is entirely better or worse than other solutions within the surface). In other words, some solutions may have very good result for the first measurement but not the fourth measurement. Others may have good overall measurements. Or some may have great fourth measurement and first measurement but not the second. So the "surface" is like a set of tradeoffs among objectives.

During the search, the "+" symbols in the original Z340 are replaced with other symbols, then the measurements are taken. At each generation, candidate assignments are mutated and kept if they are pareto optimal with other candidates.

Here are some preliminary results after 1200 generations: https://docs.google.com/spreadsheets/d/ … sp=sharing The spreadsheet is sorted by the composite score, which is the product of all 4 scores, to help the overall "best" candidates to appear near the top. The original Z340 appears on line 141, so you can compare the measurements to it. The generated cipher texts are all there, too, if you want to run some solvers on them to see if they score better than the original 340.

So far, the result confirms that making such assignments can greatly increase the appearance of "interesting things" (repeating ngrams, repeating fragments, and homophone cycles).

For example, the original Z340 has these improbable patterns:

4.644659E-12 +???FBc +???FBc
1.12791E-11 J??p7 J??p7
2.589325E-11 #O???Y #O???Y
4.1108127E-11 5?4?. 5?4?.
4.51164E-11 H???p?^ H???p?^
5.8259814E-11 O?*?C O?*?C
1.0193137E-10 G2 G2 G2
2.5692576E-10 M??2?c M??2?c
3.1719227E-10 |5F |5F
4.7190446E-10 2?c 2?c 2?c

The cipher at line 4 of the spreadsheet has these improbable patterns:

5.159943E-16 J??#?%??Y J??#?%??Y
1.3209456E-15 #?%??Y?< #?%??Y?<
2.0639773E-15 J???O%??Y J???O%??Y
2.0639773E-15 #O%??Y #O%??Y
3.224964E-15 J??#O% J??#O%
4.643948E-15 z?JS??7 z?JS??7
5.283782E-15 O%??Y?< O%??Y?<
5.6191785E-15 JS?p7 JS?p7
5.7332704E-15 J??#O???Y J??#O???Y
1.1888509E-14 S??j??5F S??j??5F

(As I look at those, I wonder if the scores need to be normalized to avoid overcounting any repetitions)

Similarly, the original Z340 has these improbable homophone cycles:

+B, [+B] B+++++++++ [+B] + [+B] [+B] [+B] [+B] + [+B] [+B] + [+B] + [+B] B+, 10, 9.2118554E-27
2z, [2z] [2z] 2 [2z] [2z] [2z] [2z] [2z] [2z] z, 8, 5.8105547E-26
|c, [|c] [|c] [|c] [|c] | [|c] c [|c] c [|c] [|c] |, 8, 3.135721E-25
p|, [p|] ppp [p|] [p|] [p|] [p|] || [p|] [p|] [p|] , 8, 6.721697E-25
BO, [BO] [BO] OO [BO] B [BO] BBB [BO] [BO] [BO] [BO] , 8, 1.3483034E-24
Bc, B [Bc] c [Bc] B [Bc] B [Bc] c [Bc] [Bc] [Bc] B [Bc] , 8, 1.3483034E-24
lM, [lM] [lM] [lM] [lM] [lM] [lM] [lM] , 7, 2.4584872E-24
RK, [RK] [RK] [RK] [RK] [RK] R [RK] [RK] , 7, 6.2605362E-24
RM, [RM] [RM] [RM] R [RM] [RM] [RM] [RM] , 7, 6.2605362E-24
2M, [2M] [2M] 22 [2M] [2M] [2M] [2M] [2M] , 7, 1.4278389E-23

The cipher at line 28 of the spreadsheet has these:

Rc, [Rc] R [Rc] [Rc] [Rc] c [Rc] [Rc] [Rc] [Rc] [Rc] cc, 9, 1.3996231E-27
Bc, B [Bc] cc [Bc] [Bc] [Bc] B [Bc] c [Bc] [Bc] [Bc] B [Bc] , 9, 7.2217504E-27
cF, [cF] F [cF] F [cF] [cF] c [cF] F [cF] cc [cF] [cF] [cF] , 9, 7.2217504E-27
(K, [(K] [(K] [(K] ( [(K] [(K] [(K] [(K] [(K] , 8, 2.2646309E-26
OK, [OK] [OK] [OK] [OK] [OK] [OK] [OK] OO [OK] , 8, 5.2608665E-26
Rl, [Rl] [Rl] R [Rl] [Rl] [Rl] [Rl] [Rl] R [Rl] , 8, 5.2608665E-26
l|, [l|] [l|] [l|] [l|] [l|] [l|] [l|] [l|] ||, 8, 5.2608665E-26
2(, [2(] (2 [2(] [2(] [2(] [2(] [2(] [2(] [2(] , 8, 5.8105547E-26
(M, [(M] [(M] [(M] ( [(M] [(M] M [(M] [(M] [(M] , 8, 5.8105547E-26
2M, [2M] [2M] [2M] 2 [2M] [2M] [2M] [2M] M [2M] , 8, 5.8105547E-26

(I’m wondering if the scoring here should be modified to count ONLY the contiguous sequences, to reward the appearance of unbroken cycles)

I think it will take a lot of work to test the wildcard hypothesis, but a good start will be to do as smokie suggests and compare distributions of random shuffles to the original 340, and also to generate more test ciphers with known solutions that use wildcards in the way we assume it is being done. If the solvers can break those test ciphers but not the 340 then we can exclude this hypothesis.

Thanks doranchak.

I understand the last part. I hope that you can help with the random sequence data. I could make the distribution graphs if you want, but to randomize, find sequences, compile totals for all scores, etc. would take me eons. Actually, I couldn’t because my computer starts smoking when I try to use Excel to examine even the L=3 sequences.

Whenever you get the chance.

I think that you are also saying that you are going to create other ciphers with, known solutions, the sequencing and using wildcards to see if your computer programs can solve them as compared to the 340. Thanks again.

EDIT: Also notice the graph above for L-3. The distributions are different. That probably took me a day just for one randomization. I think that maybe the comparisons between the distributions will be different for L-4, L-5,, L-6, and L-7 because the L-3 comparison is different than the L-2 comparison.

So far, the result confirms that making such assignments can greatly increase the appearance of "interesting things" (repeating ngrams, repeating fragments, and homophone cycles).

But how do we measure its significance? I’ll see if I can score these ciphers you included in the document.

Edit: doranchak, the ciphers in your document have different lengths. I’m not sure what’s the problem here.

I made a cipher with perfect cycles and with the letter "a" (became "=" symbol) not homophonically substituted (count 24). I’m not sure if it could be of use but it looks interesting. It makes me think that which we are seeing as wildcards could just be letters that have no homophones.

p14hs63a24.txt

zL6ZQi1~Vf0'7?#Ko
E]{+BpYSwnE=^GlN
&fIQ%G‚gMk6@l$J1w
G#)c=(2%=/0R97T=
‚D.?^K5vl+:ownr3|
pNzYLGZ{]IMV~(2=R
c6:l/SC&1im0'^€.3
gkG7!KzQr+p=J=$@?
#ND]oCS=|nl‚)9QvV
M&RT6@f1%G$g.=i0
r:=37w~=#Dz=%=‚n
]LKY{?w+2=ZpfN='
V=$=lkoB=|G&RS/i=
:lZ.M/%€rGQ#YIlZc
('V/?k6~&E=391|^G
)Tzf0wL=m7]{ovgI
R=.r€iK@Yc+‚9p%NB
:TM'LlV{Sv&63I1k0
=zcG.D7=]9lRGrQ$K
?E:fo+!lnp#3w~@NV

(I’m wondering if the scoring here should be modified to count ONLY the contiguous sequences, to reward the appearance of unbroken cycles)

A road in between perhaps.

I think it will take a lot of work to test the wildcard hypothesis, but a good start will be to do as smokie suggests and compare distributions of random shuffles to the original 340, and also to generate more test ciphers with known solutions that use wildcards in the way we assume it is being done. If the solvers can break those test ciphers but not the 340 then we can exclude this hypothesis.

I’ll create a wildcard cipher upcoming weekend (maybe sooner, can’t promise) by hand, do you guys agree on 4 wildcard symbols with the same frequencies as (5, 19, 20, 50) seen in the 340? I’ll try to mask obvious repeating ngrams visually.

But how do we measure its significance? I’ll see if I can score these ciphers you included in the document.

Maybe the strong patterns in the original 340 can be ranked by the relative probability, weighted against whatever the shuffle tests show as the distribution of naturally-occurring patterns. Then you’ll at least have a sense of which patterns escape the reach of pure randomness.

But the patterns I’ve introduced by my multiobjective search are arrived at using artificial means (i.e., creating candidate alternative ciphertexts). So the only real ranking we can do is to look at other patterns that might be "unlocked" by our guesses of the wildcard assignments, or by applying a strong solver to each candidate until the correct one is identified.

I don’t even know if the approach I’m using is effective, since I haven’t applied any test ciphers to it yet.

Edit: doranchak, the ciphers in your document have different lengths. I’m not sure what’s the problem here.

I forgot to say that my search includes nulls as one of the symbols a wildcard can be replaced with.

I’ll create a wildcard cipher upcoming weekend (maybe sooner, can’t promise) by hand, do you guys agree on 4 wildcard symbols with the same frequencies as (5, 19, 20, 50) seen in the 340? I’ll try to mask obvious repeating ngrams visually.

My view is that we should start simple, and only assume the + is a wildcard. If your solver can deal with those tests, then expand the wildcards to more than one symbol, until the solver can handle all 4 wildcard symbols effectively. Then you’ll be fairly confident that you’ve excluded the hypothesis for the real 340 (or you’ll actually crack the damned thing. PLEASE DO THAT! )

Yes, I agree that symbols 5, 19, 20 and 51 are the four hot candidates for wildcards, fillers or 1 to 1 substitutes. They are high in count but, unlike the other symbols (excepting those that are very low in count), absolutely do not cycle well with any other symbols.

And I agree with starting simple.

To state the obvious, I think that now that we have resolved that Zodiac used cycles, there are two issues before us. How to identify the small handful of cycles that he actually used, and also how to eliminate the wildcard hypothesis.

On these issues I defer to your judgment greatly. The multiplicity of observed cycles can be examined under different lenses. The distribution lens is one. I also like the shuffling lens. Simple scoring methods will screen out many. Perhaps the wildcard analysis will yield another fact that we did not know. At the least, that will narrow down the use of those hot candidates as either filler or as 1 to 1 substitutes.

Thank you and I’ll be back.

P.S. I have a question about your computer programs. I see that you have been using your own symbol set. I was just wondering if your programs work with the actual symbols, or if the programs work with numbers and convert to symbols. The reason that I ask is because I noticed that you have started referring to the symbols by number instead of by symbol.

Maybe the strong patterns in the original 340 can be ranked by the relative probability, weighted against whatever the shuffle tests show as the distribution of naturally-occurring patterns. Then you’ll at least have a sense of which patterns escape the reach of pure randomness.

But the patterns I’ve introduced by my multiobjective search are arrived at using artificial means (i.e., creating candidate alternative ciphertexts). So the only real ranking we can do is to look at other patterns that might be "unlocked" by our guesses of the wildcard assignments, or by applying a strong solver to each candidate until the correct one is identified.

I don’t even know if the approach I’m using is effective, since I haven’t applied any test ciphers to it yet.

I’m scoring your ciphers now with up to 6-grams and a very high amount of keys to make sure they are maxed out.

Edit: your ciphers will not be done before I have to go to work. I will make another reply this evening with your results.

My view is that we should start simple, and only assume the + is a wildcard. If your solver can deal with those tests, then expand the wildcards to more than one symbol, until the solver can handle all 4 wildcard symbols effectively. Then you’ll be fairly confident that you’ve excluded the hypothesis for the real 340 (or you’ll actually crack the damned thing. PLEASE DO THAT! )

Well in this thread we already explored a 340 character part of the 408 with the "+" symbols from the 340 superimposed but that is only 53 symbols. Both ZKDecrypto and AZdecrypt can solve that but the score is quite low because the patterns of text are interrupted and the higher level n-grams cannot lock in as much. I’ll make a few ciphers, ranging from 1 to 4 wildcards or so.

By the way I tried something else. I superimposed the 4 suspected wildcards on a 340 part of the 408 and then removed them. Scored this both in ZKDecrypto and AZdecrypt and it didn’t catch on. Here is the cipher and the plaintext for which the wildcards were removed also. This is not the plaintext that came out of a solver, it’s the actual one.

408 wildcard simulation:

ilikkillingpeople
auseitissomucfuni
ismorefunthaillin
gwlameinteforrete
cauemaisthemotdan
geousanimalofallt
okillsoethiggives
ehemtthrillingepe
eceiseenbetterang
ettingyourrocksfi
thagilthestpartfi
tisthatwhedeiwill
berebornnparaicen
dalltheihvekildwl
lbomemyslavesiwil
otgiveoumnamebeca
ueyouwilltr
¼ºP//uBºËOR¥ÐX¥BW
GyF°¼HP¹K‚ÑyÅJy^u
˽ÑTÔNQyDµ£S¼·BPO
RAºÌÑEË^LZJÄÒÐHW
žy+ÑG¼KI£°ÑXµ¤S¢
RNIyEÌO¾ÑGBTQS·BL
Ä/P·B¹XEHMuRRËÃZK
УWѵLMÒ¼·BPDR+¥°
NÅEËFZÐOVWIµ+ÔÌ^R
°HI¼DR¸TyÒÄÅ/¹JP
µM¾RuºL£EKH¥GÒIJË
µ¼¾LMÌNA£Z¤ÐËA¼·B
VW+VTÔO^¥SÒÌuÅ°D
¤GººIMNË£ÃE/¼ºÆA·
BVXÑWѸF·¾Ã+¹¼A¼º
TµRuÃ+ÄyÑ^SÑWVZÅG
yE¸TyA¼º·LÔ

Then I made a simple change to my solver to remove characters at random in the corpus! This is after I remove all other garbage characters that are not "abcdefg…". I wonder if this idea can be improved, any thoughts?

if rnd>0.15 then
'process letter
end if

Then scored the 408 example above and amazingly one of the results came out rather decently, given the circumstances.

ilaffallindpeople
auseinatherumhusa
idrourfunshaillan
dwleroistthorvene
meusraihtherostan
drtuoeneralofallt
ofalltoonhaddinth
ehersthrillandspe
rmoistencetssuesd
entindyoursomftha
shedalthohnparthi
sietherwhtteiwill
cesscounspareamen
tallthrihnofilewl
lcoreryslenstiwil
osdansoursarectma
uoyouwilltu

Some catch though, this is one of 300 files, it’s not a high scoring one and if you don’t know the plaintext… I did this for the 340 and here are the results, I checked them but I really don’t know if there is anything. 1. hypothesis has to be correct. 2. wildcards have to be correct.

Results for the 408 and 340 for various percentages of removed characters from the corpus.

Observations for the results of the 408, many returns seemed to have at least the right consonants/vowels in place. I will add something to my solver that after each return records the consonant/vowel of each position to a map by simply adding or subtracting 1. And then see if I can get at least a lock on the consonants/vowels.

Yes, I agree that symbols 5, 19, 20 and 51 are the four hot candidates for wildcards, fillers or homophones. They are high in count but, unlike the other symbols (excepting those that are very low in count), absolutely do not cycle well with any other symbols.

Made a cipher with 63 symbols, uses perfect cycles (computer generated) but has 4 symbols which have a 1 to 1 substitution, so no homophones (counts are rather similar to the suspected wildcards of the 340). They should also not cycle well, you should be able to identify them by frequency. I wonder what you could say about it. It does solve but that’s not the issue which I’d like to explore here.

p70chs63.txt

[VK]EXk;,nHRix(^m
B^"wpvS}sH/‚YFDq
$bo|=ƒgblb&_-uwRG
x9Ma^'b1*:Q~.;4,
p2|X([^}"TunbUMb
FVQi]@vqDYƒ[-K2Eo
YbU]^g.t$l:&b/Y,n
_Vk'm=p9b*v(;RYF
4+|XuGbM}ql-Q.,
2po_ƒSi|Y:‚b'xYKg
su1*(bFVM"/bt9wQ
~DY.[q-,@=EypkBm$
Xnlb}|Sob_:u;Rg^9
MXsx}yHi"U‚&^/4D
'$v*VQYK\b1(-.ƒ:
E]koFba=RgB+mS9Y
,qblVx[Y-‚bnKY_"X
yEv2bwp;k'biƒmUb}
B|S/*:&D=ut‚(M;Ko
sE$i[Vk]mgn^2Ub9F

P.S. I have a question about your computer programs. I see that you have been using your own symbol set. I was just wondering if your programs work with the actual symbols, or if the programs work with numbers and convert to symbols. The reason that I ask is because I noticed that you have started referring to the symbols by number instead of by symbol.

I’m not using the webtoy transcription but I should switch to it because it is easier to work with. In computer programs these symbols are usually converted to numbers (integers) because the CPU can process integers faster.

Yes, I agree that symbols 5, 19, 20 and 51 are the four hot candidates for wildcards, fillers or homophones. They are high in count but, unlike the other symbols (excepting those that are very low in count), absolutely do not cycle well with any other symbols.

Made a cipher with 63 symbols, uses perfect cycles (computer generated) but has 4 symbols which have a 1 to 1 substitution, so no homophones (counts are rather similar to the suspected wildcards of the 340). They should also not cycle well, you should be able to identify them by frequency. I wonder what you could say about it. It does solve but that’s not the issue which I’d like to explore here.

EDIT: 1 to 1 substitutes.

It sounds to me like you are experimenting with your computer programs that solve coded messages, and using models that are similar to what I am suggesting about the sequences, wildcards, and other possibilities for the four candidate symbols.

Your Question

I think that you are wondering if the results of an analysis of this new model would be similar to the results of my analysis of the 340. Using my rudimentary scoring system of two symbol cycles. I think that you are wondering if my method would flush out the same four symbols. I could do that, it would take a few hours at least. But it would be nice if you could convert the symbols to numbers for me, starting with [=1, V=2, etc., just like how my version of the 340 is numbered. I have a simple spreadsheet that compares each symbol to every other symbol, and has 63*62=3906 different two symbol sets to work with and look for patterns. I could convert your symbols to numbers by myself, but it would take a while. I do a lot of this stuff manually. But I would definitely like to try flushing out your four symbols if that is what you are asking for. If I can, it would mean that I could have flushed out four symbols in the 340 that merely have a 1 to 1 substitution.

Is that what you are thinking?

Your model uses perfect cycles, which raises an interesting question for me. Almost all if not all of the long and/ or multi repeated cycles in the 340 are missing symbols. If the wildcard hypothesis is correct, then the total number of missing symbols in the cycles would be roughly the same as the wildcard count. I think that if your model had roughly the same number of missing cycle symbols, I am curious to find what my analysis would show.

I would be happy to try with the perfect cycles or with the cycles with missing symbols.

Thanks for answering the question about the conversions of symbols to numbers and vice versa. You must a a subroutine that does that as an aside to the work that your computer is doing. Numbers do make programming easier.

Distribution Comparison Method Revised

In the interest of being thorough, I will finish my expressed thoughts on the distribution comparison method for isolating Zodiac’s symbol cycles:

In a post above, I was talking about making 30 randomizations, and comparing the mean count of each score to the count for each 340 score. I was using a score system of 0% to 99%, or one hundred possible score slots. However, I mentioned about possible including the standard deviation for each mean count as well. To finish and document this thought for future reference:

To concisely revise, a standard deviation value could be added to the mean. Any 340 cycle that scored higher than the mean plus the standard deviation would be more likely to be Zodiac made rather than random. And the nice thing about the method is that the standard deviation value could be adjusted to 1.2 standard deviations, 1.4 standard deviations, or whatever to eliminate more and more cycles from the huge list of cycles that we are working with.

It’s just one possible tool. I really liked the shuffle idea. And there are more methods that we can apply as we learn about the nature of the cycles.

Thanks, S.T.

Here are your ciphers doranchak. I should be able to process them faster next time. The scores are normalised over the amount of characters "score * 340 / c", I could possible also include normalisation over the amount of symbols "score * 340 * 63 / c / s" or anyway you want it. I copied the ciphers of your document as they appear and numbered them from top to bottom.

I think that you are wondering if the results of an analysis of this new model would be similar to the results of my analysis of the 340. Using my rudimentary scoring system of two symbol cycles. I think that you are wondering if my method would flush out the same four symbols. I could do that, it would take a few hours at least. But it would be nice if you could convert the symbols to numbers for me, starting with [=1, V=2, etc., just like how my version of the 340 is numbered. I have a simple spreadsheet that compares each symbol to every other symbol, and has 63*62=3906 different two symbol sets to work with and look for patterns. I could convert your symbols to numbers by myself, but it would take a while. I do a lot of this stuff manually. But I would definitely like to try flushing out your four symbols if that is what you are asking for. If I can, it would mean that I could have flushed out four symbols in the 340 that merely have a 1 to 1 substitution.

Is that what you are thinking?

That’s part of what I’m thinking. I would also like to know if you find possible broken cycles in relation to these 1:1 symbols. There should be none but I’m thinking that some may show up out of chance. And how does this compare to the 340? Do you see more or less? Take your time, when you’re done I’d like to give you the same cipher but with some randomisation applied to the cycles.

p70chs63.txt
-----------------
Symbols: 63
Characters: 340
Multiplicity: 0.1852941
Index of Coincidence: 0.0174735
-----------------
Numbered by appearance:
1:            [: 6
2:            V: 7
3:            K: 6
4:            ]: 5
5:            E: 6
6:            X: 6
7:            k: 6
8:            ;: 6
9:            ,: 6
10:           n: 6
11:           H: 3
12:           R: 5
13:           i: 6
14:           x: 5
15:           (: 6
16:           ^: 8
17:           m: 6
18:           : 11
19:           B: 4
20:           ": 5
21:           w: 4
22:           p: 6
23:           v: 5
24:           S: 5
25:           }: 6
26:           s: 4
27:           /: 5
28:           ‚: 5
29:           Y: 12
30:           F: 6
31:           D: 5
32:           q: 5
33:           $: 5
34:           b: 23
35:           o: 6
36:           |: 6
37:           =: 5
38:           ƒ: 5
39:           g: 6
40:           l: 5
41:           &: 4
42:           _: 5
43:           -: 6
44:           u: 6
45:           G: 2
46:           9: 6
47:           M: 6
48:           a: 2
49:           ': 5
50:           1: 3
51:           *: 5
52:           :: 6
53:           Q: 5
54:           ~: 2
55:           .: 5
56:           4: 3
57:           2: 5
58:           T: 1
59:           U: 5
60:           @: 2
61:           t: 3
62:           +: 2
63:           y: 3

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
18 19 16 20 21 22 23 24 25 26 11 27 28 29 30 31 32
33 34 35 36 37 38 39 34 40 34 41 42 43 44 21 12 45
14 46 47 48 16 49 34 50 51 52 53 54 55 8 56 9 18
22 57 36 6 15 1 16 25 18 20 58 44 10 34 59 47 34
30 2 53 13 4 60 23 32 31 29 38 1 43 3 57 5 35
29 34 59 4 16 39 55 61 33 40 52 41 34 27 29 9 10
42 2 7 49 17 37 22 46 34 51 23 15 8 12 29 30 18
56 62 36 6 44 45 34 18 47 25 32 40 43 53 55 18 9
57 22 35 42 38 24 13 36 29 52 28 34 49 14 29 3 39 
26 18 44 50 51 15 34 30 2 47 20 27 34 61 46 21 53
54 31 29 55 1 32 43 9 60 37 5 63 22 7 19 17 33
6 10 40 34 25 36 24 35 34 42 52 44 8 12 39 16 46
47 6 26 14 25 63 11 13 20 59 28 18 41 16 27 56 31
49 33 23 51 2 53 29 3 18 18 34 50 15 43 55 38 52
5 4 7 35 30 34 48 37 12 39 19 62 17 18 24 46 29
9 32 34 40 2 14 1 29 43 28 34 10 3 29 42 20 6
63 5 23 57 34 21 22 8 7 49 34 13 38 17 59 34 25
19 36 24 27 51 52 41 31 37 44 61 28 15 47 8 3 35
26 5 33 13 1 2 7 4 17 39 10 16 57 59 34 46 30

[VK]EXk;,nHRix(^m
B^"wpvS}sH/‚YFDq
$bo|=ƒgblb&_-uwRG
x9Ma^'b1*:Q~.;4,
p2|X([^}"TunbUMb
FVQi]@vqDYƒ[-K2Eo
YbU]^g.t$l:&b/Y,n
_Vk'm=p9b*v(;RYF
4+|XuGbM}ql-Q.,
2po_ƒSi|Y:‚b'xYKg
su1*(bFVM"/bt9wQ
~DY.[q-,@=EypkBm$
Xnlb}|Sob_:u;Rg^9
MXsx}yHi"U‚&^/4D
'$v*VQYK\b1(-.ƒ:
E]koFba=RgB+mS9Y
,qblVx[Y-‚bnKY_"X
yEv2bwp;k'biƒmUb}
B|S/*:&D=ut‚(M;Ko
sE$i[Vk]mgn^2Ub9F

Edit: please disregard this sample I will upload a much better version tomorrow with the actual cycles included.
Is this okay Smokie? Let me know if you still want it different. Could seperate numbers by commas next time?

Your model uses perfect cycles, which raises an interesting question for me. Almost all if not all of the long and/ or multi repeated cycles in the 340 are missing symbols. If the wildcard hypothesis is correct, then the total number of missing symbols in the cycles would be roughly the same as the wildcard count. I think that if your model had roughly the same number of missing cycle symbols, I am curious to find what my analysis would show.

Excellent idea. I’ll see if I can make such a cipher for you tomorrow.

Jarlve,

What you have provided is perfect the way it is. I want to find the cycles myself. After I input the numbers, my spreadsheet will show them to me and I can sort and filter them any way that I want. Then I copy and paste the scores to another spreadsheet and total them up. The symbols with the lowest overall scores have fewer cycle relationships with all other symbols.

I will perform the exact same analysis that I performed on the 340 two symbol cycles, and give you my answer as to what symbols do not cycle well with the others. I understand that some of the non-cycling symbols may actually cycle randomly with other symbols. That is a possibility. But I will be able to show any relationships that are in question. It may take a little time; there is going to be a lot of copying and pasting going on over here.

Thanks.

doranchak, how are your results? I would like to see how your mutli-objective hill climber performs on a wildcard cipher of our own.

smokie,

First one was too easy because all 4 of them had the highest frequencies of all symbols. I’m not sure but there may also have been a problem with the previous encoder, which I wrote rather quickly a few weeks ago. Anyway here’s a better one, for which 4 symbols have a 1:1 substitution and only 1 is identifiable by frequency. Besides those everything else cycles perfectly, I’m really anxious now if you can identify them!

The cycles are also in the text file both in symbolic and nummeric version, if you don’t want to see them just don’t scroll down but it’s pretty neat! I don’t think you’ll remember them if you just glance over it.

Here’s the new one: (please use this one, sorry if I wasted your time!)

p70chs63.txt
-----------------
Symbols: 63
Characters: 340
Multiplicity: 0.1852941
Sum of non-repeats: 4387
Index of coincidence: 0.0217074
-----------------
Symbols numbered by order of appearance:
-----------------
1 = Y (c=5)
2 = a (c=4)
3 = c (c=12)
4 = U (c=4)
5 = y (c=11)
6 = F (c=10)
7 = ' (c=11)
8 = p (c=4)
9 = S (c=14)
10 = w (c=5)
11 = C (c=2)
12 = E (c=5)
13 = - (c=4)
14 = k (c=5)
15 = V (c=7)
16 = " (c=8)
17 = m (c=11)
18 = o (c=4)
19 = 1 (c=5)
20 = Z (c=3)
21 = 8 (c=13)
22 = I (c=4)
23 = J (c=10)
24 = N (c=3)
25 = b (c=1)
26 = = (c=4)
27 = n (c=12)
28 = M (c=6)
29 = s (c=5)
30 = _ (c=6)
31 = 4 (c=5)
32 = e (c=23)
33 = u (c=10)
34 = * (c=13)
35 = L (c=4)
36 = q (c=4)
37 = z (c=6)
38 =  (c=4)
39 = ! (c=6)
40 = : (c=3)
41 = 6 (c=2)
42 = 0 (c=2)
43 = & (c=2)
44 = 3 (c=6)
45 = . (c=3)
46 = > (c=3)
47 = A (c=2)
48 = ; (c=3)
49 = 2 (c=3)
50 = , (c=4)
51 = v (c=4)
52 = / (c=1)
53 = W (c=4)
54 = + (c=3)
55 = Q (c=3)
56 = 5 (c=3)
57 = r (c=2)
58 = @ (c=3)
59 = ) (c=2)
60 = O (c=3)
61 = ^ (c=2)
62 = R (c=1)
63 = B (c=3)
-----------------
Symbolic cipher:
-----------------
YacUyF'pSwCE-kV"c
mo"1Z8IyJNb='nMs_
4eu*LqFeze!:S6E0
kJ8&"3e.V>*AS;28m
*,SuMv"Fm1/8YeW*e
_+SQ5rwzsnIq@cUyJ
ne,W"u8)4!Oepn*v
3a'Vc-SFeMY_=Enzm
2^8J*0emSu!3:8*mS
58FVwyL*n>'eMkncJ
ZmS._ze!+81;eRuN*
AsnSI3@8rQyB*'oc4
FqVeJSyueMO8pEF"J
*u6kFBC-1U'm"=2s
_4vzaSncmme.!:8Y>
y,'J3e&LEuo^cmyFn
*VeM+kwn@'eIcn_1J
ByqWeZS;'zeQvc5eu
o8yp!Os-*)'3S=cF
Ny4LYa'UcJw",WeuV
-----------------
Nummeric cipher:
-----------------
1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,3
17,18,16,19,20,21,22,5,23,24,25,26,7,27,28,29,30
31,32,33,34,35,36,6,32,37,32,38,39,40,9,41,12,42
14,23,21,43,16,44,32,45,15,46,34,47,9,48,49,21,17
34,50,9,33,28,51,16,6,17,19,52,21,1,32,53,34,32
30,54,9,55,56,57,10,37,29,27,22,36,58,3,4,5,23
27,32,50,53,16,33,21,59,31,39,60,38,32,8,27,34,51
44,2,7,15,3,13,9,6,32,28,1,30,26,12,27,37,17
49,61,21,23,34,42,32,17,9,33,39,44,40,21,34,17,9
56,21,6,15,10,5,35,34,27,46,7,32,28,14,27,3,23
20,17,9,45,30,37,32,39,54,21,19,48,32,62,33,24,34
47,29,27,9,22,44,58,21,57,55,5,63,34,7,18,3,31
6,36,15,32,23,9,5,33,32,28,60,21,8,12,6,16,23
34,33,41,14,6,63,11,13,19,4,7,17,38,16,26,49,29
30,31,51,37,2,9,27,3,17,17,32,45,39,40,21,1,46
5,50,7,23,44,32,43,35,12,33,18,61,3,17,5,6,27
34,15,32,28,54,14,10,27,58,7,32,22,3,27,30,19,23
63,5,36,53,32,20,9,48,7,37,32,55,51,3,56,32,33
18,21,5,8,39,60,38,29,13,34,59,7,44,9,26,3,6
24,5,31,35,1,2,7,4,3,23,10,16,50,53,32,33,15
-----------------
Nummeric cipher for ZKDecrypto:
-----------------
1   2   3   4   5   6   7   8   9   10  11  12  13  14  15  16  3   
17  18  16  19  20  21  22  5   23  24  25  26  7   27  28  29  30  
31  32  33  34  35  36  6   32  37  32  38  39  40  9   41  12  42  
14  23  21  43  16  44  32  45  15  46  34  47  9   48  49  21  17  
34  50  9   33  28  51  16  6   17  19  52  21  1   32  53  34  32  
30  54  9   55  56  57  10  37  29  27  22  36  58  3   4   5   23  
27  32  50  53  16  33  21  59  31  39  60  38  32  8   27  34  51  
44  2   7   15  3   13  9   6   32  28  1   30  26  12  27  37  17  
49  61  21  23  34  42  32  17  9   33  39  44  40  21  34  17  9   
56  21  6   15  10  5   35  34  27  46  7   32  28  14  27  3   23  
20  17  9   45  30  37  32  39  54  21  19  48  32  62  33  24  34  
47  29  27  9   22  44  58  21  57  55  5   63  34  7   18  3   31  
6   36  15  32  23  9   5   33  32  28  60  21  8   12  6   16  23  
34  33  41  14  6   63  11  13  19  4   7   17  38  16  26  49  29  
30  31  51  37  2   9   27  3   17  17  32  45  39  40  21  1   46  
5   50  7   23  44  32  43  35  12  33  18  61  3   17  5   6   27  
34  15  32  28  54  14  10  27  58  7   32  22  3   27  30  19  23  
63  5   36  53  32  20  9   48  7   37  32  55  51  3   56  32  33  
18  21  5   8   39  60  38  29  13  34  59  7   44  9   26  3   6   
24  5   31  35  1   2   7   4   3   23  10  16  50  53  32  33  15  
-----------------
Symbolic cycles:
-----------------
Old symbol: s, homophone(s): YwIqv  (YwIqvYwIqvYwIqvYwIqvYw)
Old symbol: h, homophone(s): a:>+@O  (a:>+@Oa:>+@Oa:>+@Oa)
Old symbol: a, homophone(s): cy'  (cy'cy'cy'cy'cy'cy'cy'cy'cy'cy'cy'c)
Old symbol: m, homophone(s): U,W5  (U,W5U,W5U,W5U,W)
Old symbol: n, homophone(s): FJu  (FJuFJuFJuFJuFJuFJuFJuFJuFJuFJu)
Old symbol: r, homophone(s): p-=L;Q  (p-=L;Qp-=L;Qp-=L;Qp-=L)
Old symbol: e, homophone(s): S8*  (S8*S8*S8*S8*S8*S8*S8*S8*S8*S8*S8*S8*S8*S)
Old symbol: p, homophone(s): Cb  (CbC)
Old symbol: i, homophone(s): Ek1s4  (Ek1s4Ek1s4Ek1s4Ek1s4Ek1s4)
Old symbol: t, homophone(s): VM_z!3  (VM_z!3VM_z!3VM_z!3VM_z!3VM_z!3VM_z!3V)
Old symbol: u, homophone(s): "  ("""""""")
Old symbol: l, homophone(s): m  (mmmmmmmmmmm)
Old symbol: g, homophone(s): oB  (oBoBoBo)
Old symbol: d, homophone(s): ZN6  (ZN6ZN6ZN)
Old symbol: c, homophone(s): n  (nnnnnnnnnnnn)
Old symbol: o, homophone(s): e  (eeeeeeeeeeeeeeeeeeeeeee)
Old symbol: f, homophone(s): .  (...)
Old symbol: v, homophone(s): 0A  (0A0A)
Old symbol: b, homophone(s): &^  (&^&^)
Old symbol: y, homophone(s): 2r  (2r2r2)
Old symbol: k, homophone(s): /  (/)
Old symbol: w, homophone(s): )R  ()R))
-----------------
Nummeric cycles:
-----------------
Old symbol: s, homophone(s): 1,10,22,36,51  (1,10,22,36,51,1,10,22,36,51,1,10,22,36,51,1,10,22,36,51,1,10)
Old symbol: h, homophone(s): 2,40,46,54,58,60  (2,40,46,54,58,60,2,40,46,54,58,60,2,40,46,54,58,60,2)
Old symbol: a, homophone(s): 3,5,7  (3,5,7,3,5,7,3,5,7,3,5,7,3,5,7,3,5,7,3,5,7,3,5,7,3,5,7,3,5,7,3,5,7,3)
Old symbol: m, homophone(s): 4,50,53,56  (4,50,53,56,4,50,53,56,4,50,53,56,4,50,53)
Old symbol: n, homophone(s): 6,23,33  (6,23,33,6,23,33,6,23,33,6,23,33,6,23,33,6,23,33,6,23,33,6,23,33,6,23,33,6,23,33)
Old symbol: r, homophone(s): 8,13,26,35,48,55  (8,13,26,35,48,55,8,13,26,35,48,55,8,13,26,35,48,55,8,13,26,35)
Old symbol: e, homophone(s): 9,21,34  (9,21,34,9,21,34,9,21,34,9,21,34,9,21,34,9,21,34,9,21,34,9,21,34,9,21,34,9,21,34,9,21,34,9,21,34,9,21,34,9)
Old symbol: p, homophone(s): 11,25  (11,25,11)
Old symbol: i, homophone(s): 12,14,19,29,31  (12,14,19,29,31,12,14,19,29,31,12,14,19,29,31,12,14,19,29,31,12,14,19,29,31)
Old symbol: t, homophone(s): 15,28,30,37,39,44  (15,28,30,37,39,44,15,28,30,37,39,44,15,28,30,37,39,44,15,28,30,37,39,44,15,28,30,37,39,44,15,28,30,37,39,44,15)
Old symbol: u, homophone(s): 16  (16,16,16,16,16,16,16,16)
Old symbol: l, homophone(s): 17  (17,17,17,17,17,17,17,17,17,17,17)
Old symbol: g, homophone(s): 18,63  (18,63,18,63,18,63,18)
Old symbol: d, homophone(s): 20,24,41  (20,24,41,20,24,41,20,24)
Old symbol: c, homophone(s): 27  (27,27,27,27,27,27,27,27,27,27,27,27)
Old symbol: o, homophone(s): 32  (32,32,32,32,32,32,32,32,32,32,32,32,32,32,32,32,32,32,32,32,32,32,32)
Old symbol: f, homophone(s): 38,45  (38,45,38,45,38,45,38)
Old symbol: v, homophone(s): 42,47  (42,47,42,47)
Old symbol: b, homophone(s): 43,61  (43,61,43,61)
Old symbol: y, homophone(s): 49,57  (49,57,49,57,49)
Old symbol: k, homophone(s): 52  (52)
Old symbol: w, homophone(s): 59,62  (59,62,59)

I’m slowly getting caught up. Right now I’m adjusting my measurements and trying to optimize them for speed.

I’m still lost in the Sauce Me coming into these cipher threads is like me walking into a Rolls Royce dealership. It’s nice to look, but I know when I leave, I’ll be going home in the same car I came in.
It’s cool to see you Guys all working together as a team, and hope you Guys find something big!

Jarlve,

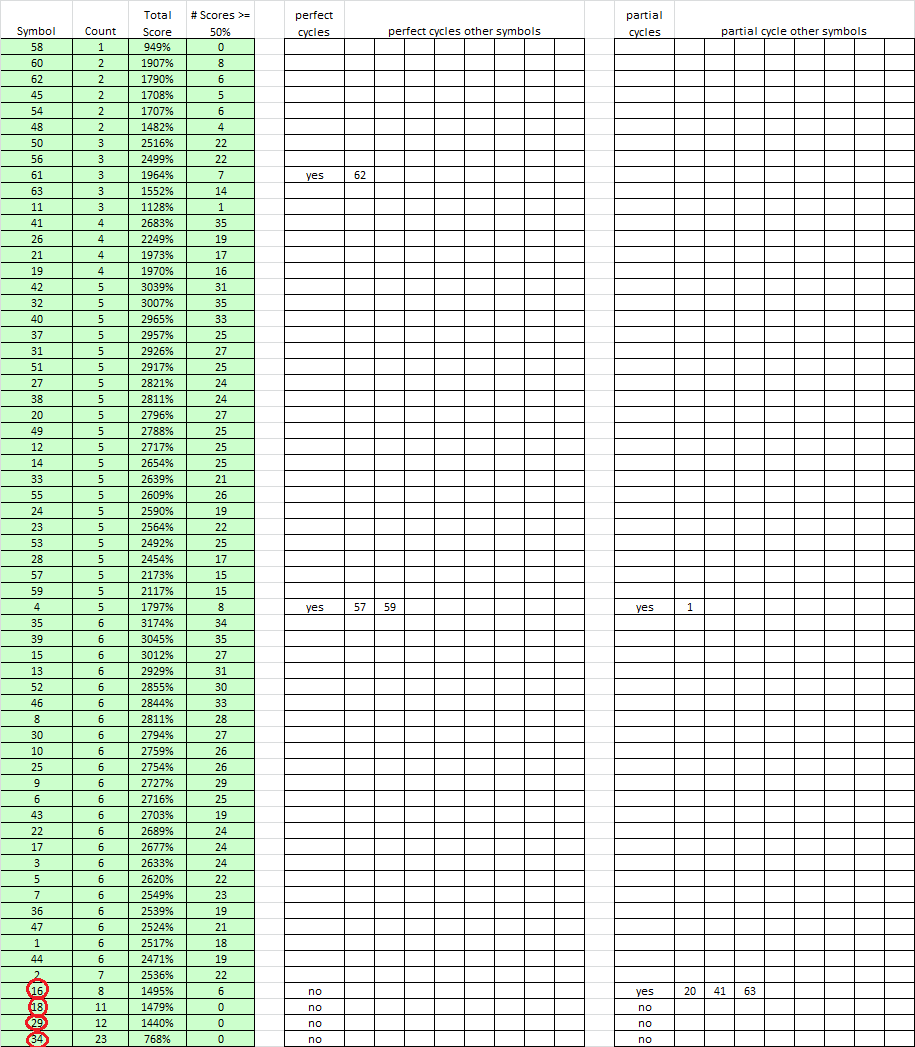
Yes, the first one was easy. Here are the results and hopefully no mistakes. I followed the same procedure as with the 340, as if I didn’t know the counts.

Experiment 1 J-ST

It seems that you intended me to find 16, 18, 29, and 34.

Symbol 16 does not have any perfect cycles with any other symbol, but does cycle with 20, 41 and 63 in part of the message.

For example, 16 and 20 (the others are similar):

I wrote another spreadsheet, and now all I have to do is enter the numbers and I can examine the one on one relationship scores very quickly. Next time don’t give me anything but a table of numbers, the ZKDecrypto version is easiest to work with. On the one you most recently posted, I won’t look at anything else.

S.T.