I think based on the varying results, it’s fair to suspect that the cipher author may have used a keyboard layout in some way to assist in making the symbol/letter assignments. But I can’t bring myself to say that a 1 out of 250 probability would be a statistical slam dunk, especially considering the variance of probability based on the initial assumptions during the randomized trials.

Also, the randomized trials assume we are only interested in finding keys that show adjacencies to typewriter key layouts. But they do not look for other adjacencies that, if present, would have generated interest among researchers (such as the periodic table, to use AK’s example). So, "odds of a random key lining up to the QWERTY layout" becomes "odds of a random key lining up to any interesting layout", a much broader criteria that would obviously increase the chances.

Still, it is a very interesting phenomenon, which reminds me of the "prime phobia" aspect of the 340. Because the "+" symbols occur a lot in the cipher, you’d expect them to fall on several of the 68 prime-numbered "slots" of the 340 cipher. But only one does. In random trials, 2.9% of shuffled ciphers with the same distribution of symbols have the same "prime-phobic" quality of the "+" symbol. Things get a little more interesting when you consider the "B" symbol, the 2nd most frequent symbol in the cipher, which is also prime-phobic: it, too, falls on only one prime-numbered spot. If you include that observation in randomized trials, you find that 1 in 143 shuffled ciphers have the same prime-phobia in its top two frequent symbols.

Rare enough to generate interest, but not so rare that it completely undeniable!

I think Doranchak states the situation pretty well. If we use pi’s analysis, we come out with 1.3% of randoms having equal or greater number of matches, which is about 1 out of 77 odds of the observed Z408 happening by chance. Using my analysis it is 0.4%, which is 1 out of 250. Doranchak states "I think based on the varying results, it’s fair to suspect that the cipher author may have used a keyboard layout in some way to assist in making the symbol/letter assignments." I agree, and would go even further, from suspecting the cipher author may have used a keyboard to suspecting he probably did.

I think Doranchak accurately states how some code and math people look at odds like these, or the prime phobic Z odds of 2.9% [1 out of 34] for the most frequent symbol (+) or 0.69 % [1 out of 143] if we include the second most frequent symbol (B).

And the frustrating things is if Zodiac was as smart as I think he was, he may have had a rough idea about some of these types of things. He didn’t tend to do things that were obvious giveaways. He avoided black and white, instead he usually kept it in the grey zone. If he was prime phobic, he did it enough to raise eyebrows but not enough to absolutely convince. If he used a typewriter keyboard, he only did it for part of his key. Again, enough to leave a tantalizing clue, but not enough times to prove he absolutely for sure did it.

I look at things a little different. We are all partially a product of our education, experience and background. My experience includes being a military policeman in the Army and a criminal defense lawyer. If in the real world I see something happen, and find out there is a 1% chance it happened randomly, I view that as a 99% chance it was not random. For example, if someone took two card decks so there were 100 cards in them and only one joker, and I go to a crime scene and see a joker card, and find that 100 card deck in the suspects house with no joker present, I look at that as a strong suspicion that the joker from that deck was placed there. Yes it is a 1% chance, but in the real world, it looks damn suspicious.

Scott Peterson never went fishing, except for the day his wife went missing. So if Scott says that was just a coincidence do you believe him? Or like a scene from the movie "The Counselor". A man is explaining that it was just a "coincidence" that a man he got out of jail was later set up and robbed of a drug shipment. The representative of the drug cartels explains "The people I work for are very practical. They don’t believe in coincidences. They’ve heard of them, they’ve just never seen one." One more movie scene analogy, from "Casino". Two slot machines get hit for huge money payoffs back to back. The casino manager asks the slot chief "Didn’t you know it was a scam, didn’t you know you were being set up?" The slot chief says "There is no way to tell that for sure." The manager says "Yes there is, there’s an infallible way. They won."

I guess that is my longwinded way of saying that yes for a mathematician a 1.3% or even 0.4% chance of something happening may not be a statistical slam dunk. But in the real world of criminals we seldom see things with those odds happen by chance. So when I see odds that something happens by chance 1.3% of the time, 1 out of 77 times (pi’s calculation) and that is what we see, I find it suspicious and worthy of further study. When I see something that happens by chance only 0.4% of the time by chance, 1 out of 250 times (my calculation), and that is what we see Zodiac did, I find it highly suspect and well deserving of much further study.

Anyway, here is a typewriter keyboard marked only with what I consider to be the slam dunk adjacent matches of plaintext-ciphertext.

They show the observed adjacent matches in the Zodiac 408 key which are:

1. . A-S
2. . B-V
3. . D-F
4. . E-W
5. . G-R
7. H-M
7. . I-U
8. . I-K
9. . R-T
10. . T-H
11. U-Y
12. V-C
13. W-A

1. I just noticed something. He seems to have started with a pretty good run with A, B, D, E, G, H. And then picks it up later to finish with another good run with R, T, U, V, W. What seems to be excluded is everything from J to Q. Which in Z408 terms means K, L, M, N, O, P are excluded, the middle range of the alphabet. Did he use something else? Was this intentional so as not giveaway to clearly that he used a keyboard for part? To keep the results in that grey range Doranchak talks about, enough to be suspicious and be a teasing clue, but not enough to be a clear result. Or just chance? Or does it mean something else? It appears he did it for the first 6 letters and the last 5 letters, but excludes the 6 in the middle. If Zodiac did NOT use the typewriter keyboard intentionally, and this is all just random, it just got weirder. How many random trials would show the first six and last five matching to a keyboard, but the middle six with no matches at all? if this is all just truly random and not intentional, shouldn’t the matches and non matches be spread out?

2. I just noticed something else! Some of the matched letters appear to "play tag" with each other. What percentage of randoms would show a similar pattern? So B=V, then V=C. In fact:

B – V – C
E – W – A – S
G – R – T – H – M
I – U – Y

Scott Peterson never went fishing, except for the day his wife went missing. So if Scott says that was just a coincidence do you believe him?

You still have to be careful. What if you arrested everyone who, on that day, were fishing for the first time in their life, and lived in the same general area? Under your premise, they all have the same probability of the fishing NOT being a coincidence. But only one or none of them would be the true perpetrator.

Without considering other evidence, you can’t directly induce a solid fact about his involvement in the crime based on the fishing fact alone. Improbable things happen all the time, and many of them are true coincidences. Recall my point about looking for one specific improbable pattern vs looking for any improbable pattern. The chances of one specific improbable pattern happening by chance is small. But if there are many improbable patterns to look for, the chances of one of them appearing gets much larger.

The birthday paradox is a good example of this. Consider a room that has 23 different people in it. What are the chances that two of them share the same birthday? Seems like a rare event, but the odds are actually 50%. Take any two people. It’s improbable that they have the same birthday. But then you look at a large number of improbable events. That is, you look at ALL PAIRS of people. If you have 23 people, you can make 253 different pairs of people. All those improbable events add up to a fairly probable one.

The fishing example is a little bit like that. You have to consider all the other improbable events that could have happened. Given enough opportunities for improbable events to happen, one of them will.

So, more evidence is always important to escape that pesky shadow of a doubt.

How many random trials would show the first six and last five matching to a keyboard, but the middle six with no matches at all? if this is all just truly random and not intentional, shouldn’t the matches and non matches be spread out?

Not necessarily. Just because something is happening by chance doesn’t mean it has to appear uniformly, or in a "non-clumpy" way. For example, if you flipped 5 coins and got heads every time, it seems non-random, but there’s still a 3% chance of it happening.

Also, there is a larger set of grouping criteria, other than the one you proposed, that have to be considered. First 5 and last 6, first 4 and last 7, first 3 and last 8, etc. You’d have to identify ALL such groupings that would be of interest, and then consider how they could still be appearing by chance.

Good points. I was really just thinking out loud. I didn’t expect to find that grouping and didn’t expect that so many letters seem to get tagged and then tag another letter. If pi or finder are still interested in looking at this maybe one or both could run 1,000,000 randoms and see the groupings and more importantly how many create linked taggings like the Z408.

Based on the results we already have your (Doranchak) statement that it is fair to suspect the cipher author may have used a keyboard layout in some fashion to assign some of the cipher symbol to letter pairings, is IMO correct. I would deem it a little stronger than you do. The question remains what does this tell us about Z and does it give us any clues to the 340? I am going to take a look at the 340 with the idea he might have again used the keyboard for part of it.

Thanks to pi for his studies, to finder for first observing and sharing this and to doranchak for his thoughts. Doranchak and I often look at things very differently, and I usually find his take very helpful (if sometimes frustrating) and needed. Sometimes we ultimately just agree to disagree, but other times he (and sometimes glurk, smithy or up2something) gave me a needed perspective that prevented me from going down blind alleys or endless mazes.

Good points. I was really just thinking out loud. I didn’t expect to find that grouping and didn’t expect that so many letters seem to get tagged and then tag another letter. If pi or finder are still interested in looking at this maybe one or both could run 1,000,000 randoms and see the groupings and more importantly how many create linked taggings like the Z408.

Well, I’ll address the groupings that you have noticed. In the z408, you have identified 2 clusters of very close letters: ABDEGHII and RTUVW.

They are not perfect clusters. The first one has 2 "holes" (i.e. it is missing the letters C and F) and the second one has one "hole" (i.e. it is missing the letter S).

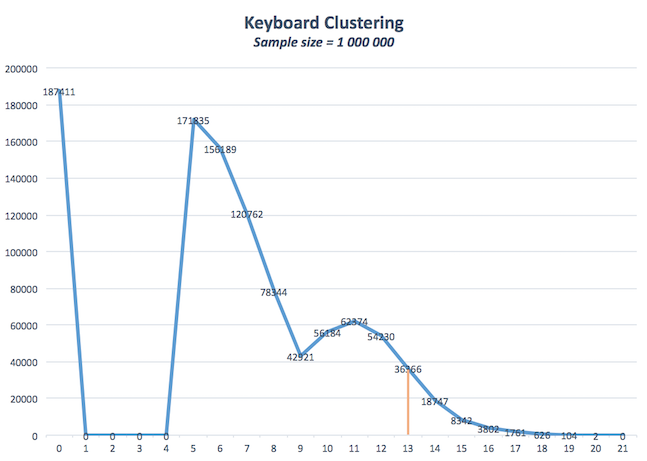
I have devised a little algorithm that randomly picks 13 letters out of 23 possibilities. Then, it counts the number of clusters that appear with a maximum of 2 non-consecutive holes per cluster. It generates 1 million of these arrangements and counts the number of results where a maximum of 2 clusters are present where their combined sizes are at least 13 characters and their individual sizes are at least 5 characters. This essentially evaluates how frequently a random key exhibits a clustering quality similar or higher than the z408.

After multiple runs of 1 million, 7% of random keys exhibit clustering configurations that show equal or higher togetherness than the z408.

The following graph illustrates an example of a 1 million run:

So, the z408 key exhibits a clustering that is higher than the mean but it is far from being exceptional.

Thanks very much for taking a look at this! Interesting.

Does your study include exclusivity? In the observed Z408 not only were there letters in two clusters but ALL the letters were in the two clusters of A-J & R-W and NONE were in the range of I-Q.

In the 7% were they exclusive like that or exclusive in any fashion?

In other words I would be very interested to know what percentage of the runs resulted in a similar grouping, were ALL the letters appear in any two clusters and NONE appear in the remaining third cluster?

I’m interested in how these results compare with other common layouts, like "AZERTY" used in Belgium and France, "QWERTZ" used in Germany, and the Dvorak layout, used by fast-typists…

-glurk

Just finished reading the thread. Very interesting discussion, some excellent points made.

To echo glurk’s post, I’d say it would be of great interest to see if a similar pattern would result from running tests on a non-qwerty layout, of which there are many. For something completely different, one could try the Arabic layout *, for instance, and see if this symbol proximity…er…thing, shows up here too.

* Which is entirely non-qwerty based, AFAIK.

Good ideas but whoa. I asked Pi to study the groupings and connections and he was nice enough to do so. I suggest let’s see what those final results are first.

Does your study include exclusivity?

That’s a very good point. I did not consider that aspect.

I just modified my algorithm to only consider clusters that encompass the totality of the chosen letters. In other words, the space between clusters do not contain any loose letters; every letter must be inside a cluster.

In such a scenario, the z408 key letter selection stands out more. Only 1.3% of 10 million random candidates show an equal or tighter clustering.

Does your study include exclusivity?

That’s a very good point. I did not consider that aspect.

I just modified my algorithm to only consider clusters that encompass the totality of the chosen letters. In other words, the space between clusters do not contain any loose letters; every letter must be inside a cluster.

In such a scenario, the z408 key letter selection stands out more. Only 1.3% of 10 million random candidates show an equal or tighter clustering.

Thanks much. That 1.3% is small enough to be very interesting for me and some others but probably not quite small enough to be interesting to everyone!

The connectivity I describe above at page 7 of this thread, B=V then V=C, etc., I’m not sure if it is possible to study that? Anyway thanks again for your work.

Thanks much.

You’re very welcome.

That 1.3% is small enough to be very interesting for me and some others but probably not quite small enough to be interesting to everyone!

I personally find it intriguing but, given all other contextual parameters, not convincing.

The connectivity I describe above at page 7 of this thread, B=V then V=C, etc., I’m not sure if it is possible to study that?

It is possible but it would require a different logic to be implemented. I’ll see what I can do but I make no promises…

I’m interested in how these results compare with other common layouts, like "AZERTY" used in Belgium and France, "QWERTZ" used in Germany, and the Dvorak layout, used by fast-typists…

I replied to this a bit earlier but I had made an error in my calculations so I deleted the post. I will post again with proper results.

Here are the corrected values by keyboard layout. The error I initially made in the post I deleted was to compare, for example, a random key applied to the azerty layout with the z408 key applied to the qwerty layout, as opposed to comparing it to the z408 key applied to the azerty layout.

I generated 10 million random keys to compare them to the z408 key on how many directly adjacent letter symbols can be found, per keyboard layout.

qwerty: 1.3% of random keys exhibit an equal or higher adjacency than the z408 key (as seen in previous posts)
azerty: 6.48% of random keys exhibit an equal or higher adjacency than the z408 key
qwertz: 7.37% of random keys exhibit an equal or higher adjacency than the z408 key
Dvorak: 14.25% of random keys exhibit an equal or higher adjacency than the z408 key

The z408 key exhibits a higher affinity with the qwerty keyboard than with the others, in terms of number of symbol letters being directly adjacent to their plaintext letter.

Very nice work _pi, that pretty much nails it. (imho)