O.k., I went back to the original post and understand it better now. That would be like drafting the message diagonally and then shuffling the columns like shuffling a deck of cards. The "untransposed" version should have substantially the same repeat list as the un-transposed period 19, but maybe with a few more or higher scoring repeats.

I like the scatter-graph. There are some points that are much higher than the cluster, and they seem roughly evenly spaced forming a horizontal line just under 2100. They score high, even though they may have fewer repeats. Did you check into those more closely?

Note that the period 15/ 19 pattern could be period 39 or 41 if he transcribed vertically. I un-transposed all 8 horizontal / vertical directions ( two from each corner ), tried to solve ten times each, and found that the two highest scoring on average were:

Transcription left to right top to bottom ( period 15 ); and

Transcription right to left bottom to top ( period 19).

I wonder if trying to work with smaller chunks of the message would be more fruitful, considering that there could be varying transposition schemes. Maybe un-transposing the right chunk the right way…

hi guys..the other day i was running AZdecrypt for the first time just experimenting around, and after about two hours i checked it and the top line read a perfect sensible line. Is this a normal happening. Does it do this because of the way the first few lines of the 340 have no repeats. any ways what spiked my interest is that it read DEARANNAFRAIDTHAT..ANN being the wife of my poi at the time. Just more really weird zynchro shit i suppose. I took a screen shot a little later and it was changing around a little but kept coming back to that line ..left it running to see what would come out a day or two later but i forgot to flick switch at power outlet too on..DOH.. lost it except the screen shot.

It’s easy to fit sensible phrases into the beginning of Z340 for the reason you identified, but it seems unusual for such a valid-sounding combination of words to appear spontaneously. I wonder if it is the result of the ngram stats used by AZdecrypt. As an example, I think that if you seed zkdecrypto with ngram stats derived from Moby Dick, in the resulting plaintexts you’ll get some appearances of phrases specific to that novel.

Another possibility is that it may have something to do with a real solution. One can only hope!

Can you post the screen shot?

Doranchak is correct about ZKD. One of the earliest versions used ‘Moby Dick’ heavily as a text statistic source, and the word "WHALE" kept being ‘found’ everywhere. It now uses a much larger text corpus to prevent this sort of bias.

-glurk

Doranchak. Technically a screen shot ..I used the iPhone. It changed around a few times but read perfect for most of the time.. always swapping back to DEARANNAFRAIDTHAT.. I missed it at this snap. I think nothing of it unless you do.

I like the scatter-graph. There are some points that are much higher than the cluster, and they seem roughly evenly spaced forming a horizontal line just under 2100. They score high, even though they may have fewer repeats. Did you check into those more closely?

Yes, I revisited them just now and I think they are caused by the shortening of the cipher text by certain transposition operations. I believe I made the plot before I realized that i needed to normalize the azdecrypt score based on cipher length, because it is higher for shorter ciphers.

I wonder if trying to work with smaller chunks of the message would be more fruitful, considering that there could be varying transposition schemes. Maybe un-transposing the right chunk the right way…

Yes, certainly worth exploring. At the moment I am testing a new IoC measurement that is applied to repeating fragments (normal ngram repeats such as AB AB AB as well as fragments such as A??B A??B A??B). My approach is to compare their relative probabilities to those of random shuffles to get an idea of which patterns can be "culled" from the measurement, so I can focus more on the most improbable repeating fragments. Then I can apply the measurement to various transpositions to see if there’s some correlation between high values of my customized IoC measurement and restoration of the correct ordering of any underlying plaintext.

I have been thinking a lot about what you are trying to do with the new IOC measurement, even before you posted. The problem is that trying to solve every possible un-transposition is not efficient, and I think that you are trying to figure out a way to determine which un-transpositions to try to solve. It is very similar to the concept of the heatmap, where I tried to figure out at which symbol position to add a skipped symbol or delete a null so as to maximize period x repeats. Sometimes it works, and sometimes it doesn’t. Among other things, I have been thinking about ways to incorporate multiple periods into my skip-null analysis.

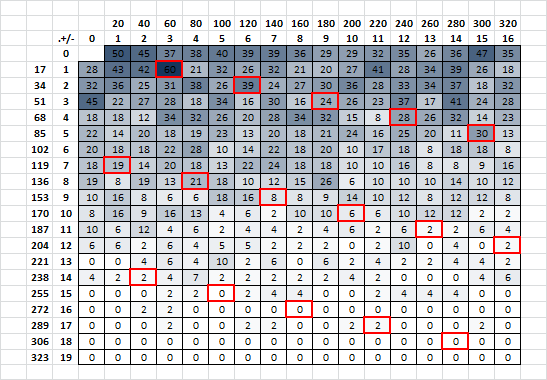
Just thinking a little bit about repeating fragments transposed versus untransposed, I made a spreadsheet suite that makes messages at period 20, with a 17 x 20 inscription rectangle. Then I applied my all-period spreadsheet for the transposed versus the untransposed. For the below, I used the "I like killing" message. The red boxes show the number of period x repeats at intervals of 20. You can see that after period 20, things do become quite confused because of randomness.

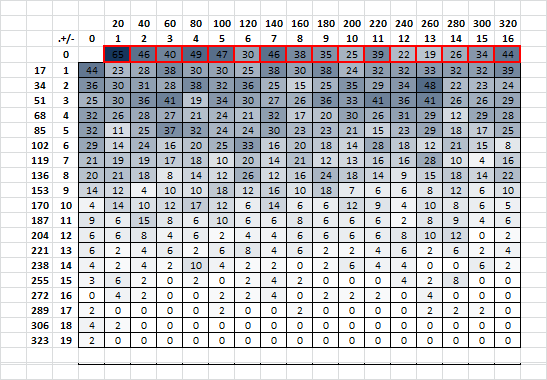
Then I untransposed the message and did the same thing. The red boxes show how period 20 becomes period 1, but with a few more repeats, period 40 becomes period 2, but with a few more repeats, etc.

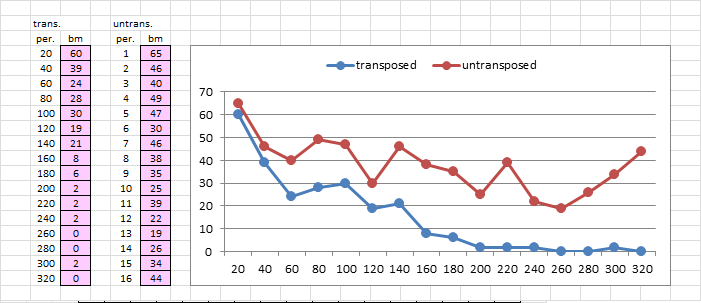
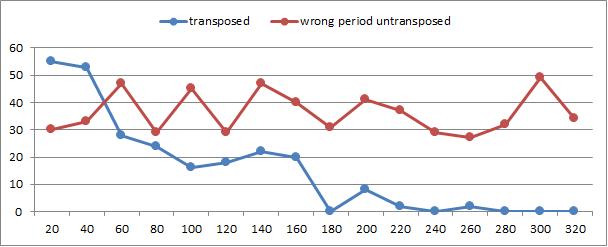
And here is a graph of the stats. The x-axis is the period, except that it only shows period 20, 40, 60, etc. The blue line shows the transposed stats, and the red line shows the untransposed stats. Notice that on the left portion of the graph, the shapes of the lines are very similar but exaggerated for the untransposed. On the the right side of the graph, the lines are not so similar and the untransposed numbers do not follow the transposed numbers.

Somewhere on the graph, maybe at about period 8 untransposed / period 160 transposed, it is not productive to make a comparison. By the way, I have made several messages this way and get similar results on the graph. I am sure that you have your IOC measurement worked out fine, but one idea that I have, and which may not work, is to find the un-transposition that maximizes the area between the lines up to about period 8 / 160. This is a very imprecise and murky subject. But I was also thinking about making such a graph for the skip-null heatmap results and finding the positions where I could delete or add a symbol to maximize the area between two lines representing transposed versions of a message.

Another observation that I do not know exactly how to explain. When I make transposed messages, usually some of the highest counts of period x repeats are still period 1 to about period 5. Conversely, when I un-transposed a message, the count of period 1 – about 16 repeats is much higher than they were at their transposed periods. For examples, the transposed message has 50 period 1 matches / repeats ( I count all matches, not just the repeats, actually ). It is not marked, but on the top all-period spreadsheet it is the upper leftmost value. On the other hand, there are only 2 count period 200 matches in the transposed message, marked by the tenth red box from upper left. But un-transposed, there are 25 such matches for period 10. It must have to do with the length of the message, at 340 symbols. You can’t get very many period 200 matches because of the length of the message. There aren’t enough period 20 possibilities. So I guess that I just explained it to myself. The length of the message has an effect on the count of period x untransposed matches versus the count of period x * transcription rows / columns matches. Does that make sense? That must be one of the reasons, if not the only reason, why the red line is an exaggerated version of the blue line on the left side of the graph, and diverges on the right side of the graph.

In short, it is likely much more productive to stay with period 1 – maybe period 8 or lower when making transposition versus untransposition comparisons.

I have been fiddling around with smaller chunks and expanding high count low cycle symbols. And I have also been thinking about un-transposition shortcuts. Regardless of whether the inscription rectangle may have been 15 or 19 columns or rows, there must be some gibberish symbols and trying to un-transposed an incomplete rectangle will cause some symbols to be switched in their positions. I have been thinking about ways to identify the most likely symbols to expand during untransposition. Not because of polyalphabetism, but to correct for erroneous un-transpositions.

Doranchak. Technically a screen shot ..I used the iPhone. It changed around a few times but read perfect for most of the time.. always swapping back to DEARANNAFRAIDTHAT.. I missed it at this snap. I think nothing of it unless you do.

Cool – Thanks for posting that.

I have decided to pursue these graphs for a while longer. I find them interesting.

Here is a message, I like killing, transposed at period 20 with a 17 x 20 inscription rectangle. Symbols 1 and 14 map to more than one high frequency plaintext so that I could get a similar distribution and bigram repeat count.

23 11 20 1 24 48 18 51 56 30 12 52 25 45 9 37 13
14 31 5 32 6 16 38 39 15 11 42 12 26 57 27 53 14
25 43 23 7 1 14 24 14 54 28 51 34 46 29 49 37 15
38 21 41 11 2 22 42 40 8 28 7 39 25 14 2 41 26
35 19 1 18 4 17 27 47 1 36 52 2 12 3 1 33 13
39 54 30 14 15 5 61 19 27 58 4 57 11 18 54 29 55
53 31 16 24 50 32 14 60 12 42 25 51 26 10 12 34 27
50 1 49 24 24 40 49 1 49 20 44 52 54 14 25 33 26
29 62 57 12 31 14 48 38 45 53 39 41 11 12 14 46 31
50 32 8 27 48 13 61 33 26 35 19 47 21 23 35 35 14
14 45 52 52 6 15 32 31 62 42 24 53 40 59 11 12 35
13 41 14 46 40 22 14 15 4 32 3 40 55 1 26 47 26
49 36 4 14 50 38 51 7 11 1 45 38 12 56 54 58 18
48 13 33 52 42 30 20 53 8 21 29 6 14 14 9 9 15
34 27 43 49 16 9 6 50 42 1 52 14 2 48 12 59 5
3 58 49 62 33 15 42 55 18 14 52 17 1 22 23 38 40
49 14 42 31 25 25 37 33 40 35 38 3 7 9 1 18 45
51 19 17 14 15 46 30 31 59 4 51 44 54 52 36 3 4
33 19 26 27 14 16 44 39 1 53 33 1 34 47 30 8 20
12 55 37 31 23 32 48 14 58 1 24 25 14 6 33 15 62

Check out how the un-transposed graph is very similar in shape to the transposed graph, but with higher counts of period 1, 2, 3, etc. bigram matches as compared to period 20, 40, 60, etc.

I am wondering if there is a way to use the shapes of the graphs to get at least a rough idea of whether we are un-transposing a message correctly, or whether there are transcription skips or nulls.

If I un-transpose at period 21, the transposed and un-transposed are expectedly dissimilar:

What would happen if I introduced just one transcription skip and un-transposed at the correct period?

EDIT: The graphs below are inaccurate, as I had a spreadsheet issue. I plan on revising the spreadsheet and posting new results soon.

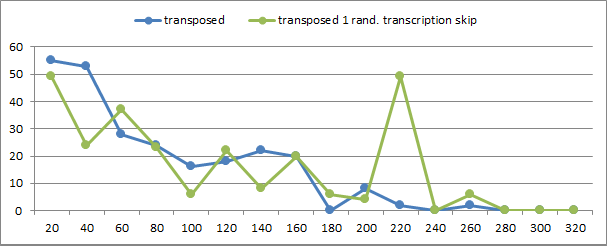
So I did introduce just 1 transcription error, a skip. Below, the blue line is the transposed version, without the skip. The green line is the transposed version with the skip:

This is what happens when I un-transpose the message with the transcription skip, the purple line. Note that the purple line is not the same shape as the green line:

My lunch break is almost over, but note also the spike at period 220 for the transposed with 1 skip. For some reason that has happened for the last few messages that I have made.

I had to make another message because I wanted to show the misalignments caused by the transcription in the middle of the untransposed message. The other one was on the edge and not easy to show. I put the transposition skip at position 162. Here is the transposed message.

Smokie30

23 11 20 1 26 48 18 51 56 30 12 52 25 45 9 37 13
14 31 5 32 6 16 38 39 11 11 40 12 26 57 27 53 14
1 44 23 7 1 13 24 14 54 28 14 34 46 29 49 37 15
38 21 41 11 2 22 42 40 8 28 7 39 25 14 3 41 26
35 19 1 18 4 17 27 47 4 36 52 2 12 3 1 33 13
37 55 30 14 15 5 61 19 23 58 4 56 11 18 54 29 55
53 31 16 24 50 32 14 60 12 40 25 51 26 10 13 34 27
50 1 49 23 24 41 48 1 48 14 44 52 54 14 25 30 26
28 62 56 15 30 15 49 38 45 53 39 40 15 14 14 46 31
48 32 7 27 48 13 62 33 1 34 19 47 21 23 36 34 14
14 45 51 52 5 15 30 31 62 40 24 53 40 59 12 12 36
15 40 14 46 42 22 22 15 2 32 4 41 55 39 25 47 26
49 36 4 14 50 37 51 7 11 1 46 38 12 56 55 58 18
50 13 33 53 42 30 20 53 8 21 29 5 14 14 9 10 15
36 27 43 49 17 9 6 50 42 1 51 11 4 48 11 59 5
3 58 49 61 31 13 40 54 19 14 52 16 39 20 1 39 41
49 14 42 33 25 25 38 31 40 35 38 4 7 10 1 18 46
53 18 16 14 11 47 31 31 59 2 51 44 54 52 35 3 4
30 18 26 23 11 17 43 39 1 14 33 27 34 47 30 7 22
12 55 37 31 26 32 48 14 58 1 24 24 21 6 33 12 62

EDIT: The graphs below are inaccurate, as I had a spreadsheet issue. I plan on revising the spreadsheet and posting new results soon.

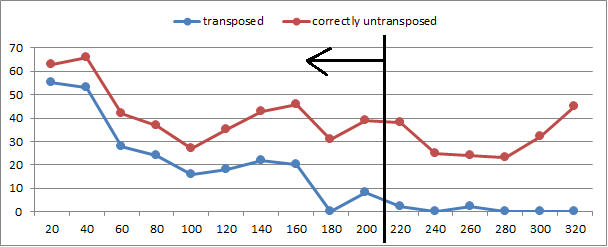
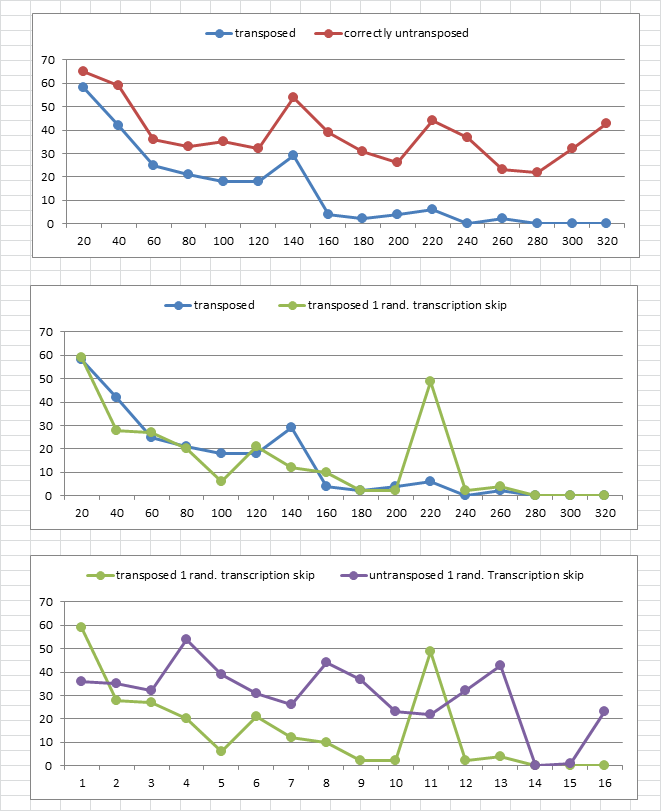
Here are the graphs. At top, the message transposed versus correctly untransposed. No skips. See that the shape of the lines are similar. In the middle, the transposed without the skip, versus the transposed after the skip. Relatively subtle differences, except the strange spike at period 11 / 220. At bottom, the transposed with the skip versus the untransposed with the skip. As opposed to the top graph, the shapes of the lines are very different.

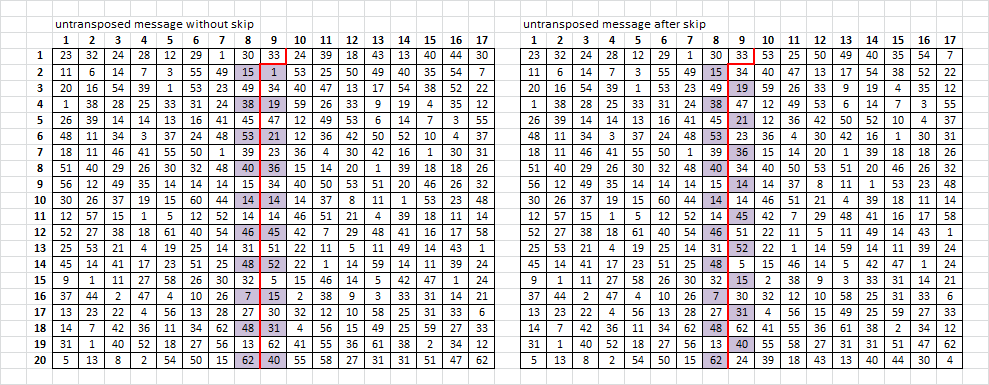
Why? Because of the misalignment caused by untransposing with a skipped symbol. Below is the message, untransposed without the skip on the left, and untransposed with the skip on the right. I highlighted some of the cells at the misalignment line for clarity.

When there is a skipped plaintext during transcription, the result is two very different shaped lines because the periods are all mixed up. If there is no skip, then the periods are as they should be before and after untransposition, and the lines will be more similar, as with the top graph.

I haven’t looked at the 340, and don’t know how to untranspose it anyway. But the general concept is that if we are untransposing correctly, the shapes of the before and after untransposition should be very similar. The 340 must have some gibberish nulls because 340 is not a multiple of either 15 or 19. Nulls would cause similar misalignments. And there could be other variables to examine.

I was thinking about a way to identify skip or null positions. Here is the idea:

1. For each of the 340 positions, add a new symbol, say, 64, and also delete a symbol. This would make a new untransposed message to correct for transcription errors or intentional nulls.

2. Untranspose the 340 new messages. EDIT: 680 new messages because there is one new message at each position for a skip and also for a null.

3. Compare the graphs for the 340 EDIT: 680 new transposed messages to the graphs for the 340 EDIT: 680 untransposed messages. See which ones have graph lines that are most similar. The alteration with the most similar graph lines is most likely to show the position for a skip or a null.

4. Make the change and keep doing that for situations where there may be multiple skips of nulls? The method would allow for backtracking to correct for errors because we could always add a symbol where a symbols was prior deleted, or vice versa. Keep doing that until the graph lines are most similar and no improvement can be made.

Anyway, that is one idea. The general concept, though, is that a correctly untransposed message will have a graph line that is similar to the transposed message graph line, and perhaps that concept can be applied to other transposition variations.

Nice work, smokie – I will comment further when I get a chance to think about your results.

Thanks. I am very excited about the new concept of comparing transposed period x match graph lines with untransposed period x match graph lines, and am going to flesh out these concepts in more detail.

This morning I untransposed the 340 period 19. As if he transcribed into the message rectangle left right top bottom. I re=-drafted the message into 19 columns to make the repeats line up vertically, rotated the message 90 degrees, and then re-drafted that into a 17 x 20 rectangle. I was very surprised by the results. The graph lines are nearly identical in shape. Perhaps we can use this technique to eliminate skips, nulls, or other transposition variations.

I will post pictures later today or tonight, and plan on making different types of transposition message with high period 15 or 19 match counts and experimenting with them.

Let me see if I can summarize your hypothesis:

1) Assume the 340 is transposed via a 17×20 inscription rectangle
2) Such an inscription, when applied, would result in a transposed cipher text that has bigram peaks in the transposed cipher text at periods 20, 40, 60, etc.
3) The count of repeats at each period is maximized when the correct untransposition is identified
4) We assume some extra step is causing misalignments (symbols added or removed, disturbing the regularity of the inscription)
5) Thus, identifying the extra step(s) and unravelling them will produce a graph of untransposed period bigram repeats that is at a maximum distance above the graph of transposed period bigram repeats (at the same periods in multiples of 20).
6) Additionally, the bigram graph for the correctly untransposed cipher will have a shape resembling the bigram graph for the transposed cipher.

Let me know if my summary is accurate. It’s a very interesting idea. You produced graphs at intervals at 20, and observed that the area between the untransposed and transposed graphs is large. What happens when you produce graphs at other intervals? Is the area always lower for other intervals? I also wonder about the effect of choosing the starting point (for instance, instead of 20 – 40 – 60 – etc, look at 1 – 21 – 41 – 61 – etc).

Your observation about the shape similarity of the two graphs is interesting. Could be useful to search for untranspositions that maximize the area and the graph similarity. Not sure how to measure the similarities — perhaps you could transpose both graphs to an common average value on the Y-axis, normalize them, and then compute the root mean square distance or some other distance metric for the two graphs. Or maybe just compare slopes (e.g., how many segments go up together, and how many go down together?)

I implemented my fragment IoC measurement but I find that it is very easy to identify false positives. First I ran a million shuffles of the Z340 to figure out the mean and standard deviation for the measurement. Then I can compute how many standard deviations away from the mean a particular untransposition’s ioc measurement is. Some of the simple untranspositions are compelling. But none of them produce any kind of spike in azdecrypt scores.

So then I took smokie27d, which is standard homophonic substitution (correct me if I’m wrong), and ran it through my transposition explorer to see if it wanders away from the "best" untransposition (which is to perform no untransposition). And it really does wander away, finding candidates untranspositions that are many standard deviations away from the expected. It may simply be that my measurement is too promiscuous when looking for repeating patterns, or I’m not doing a good job of testing for statistical significance.

This makes me very interested in correlating the ioc measurement with other ways to detect language features in the candidate untranspositions. Possibilities include cosine similiarity, contact analysis, your periodic interval graph area, etc. I need to work on making my transposition explorer produce true positives with test ciphers.

Your experiments are exciting! I look forward to hearing more about your progress.

Let me see if I can summarize your hypothesis:

1) Assume the 340 is transposed via a 17×20 inscription rectangle
2) Such an inscription, when applied, would result in a transposed cipher text that has bigram peaks in the transposed cipher text at periods 20, 40, 60, etc.
3) The count of repeats at each period is maximized when the correct untransposition is identified
4) We assume some extra step is causing misalignments (symbols added or removed, disturbing the regularity of the inscription)
5) Thus, identifying the extra step(s) and unravelling them will produce a graph of untransposed period bigram repeats that is at a maximum distance above the graph of transposed period bigram repeats (at the same periods in multiples of 20).

Not quite. I have thought that before, but am revising.

6) Additionally, the bigram graph for the correctly untransposed cipher will have a shape resembling the bigram graph for the transposed cipher.

Yes. It is the shape of the transposed versus untransposed graph lines that is important. My theory is that if a message is untransposed correctly, then the shape will be very similar. Graph periods 1, 2, 3, etc., and periods x, 2x, 3x, etc. The shapes of the lines will be very close.

Let me know if my summary is accurate. It’s a very interesting idea. You produced graphs at intervals at 20, and observed that the area between the untransposed and transposed graphs is large. What happens when you produce graphs at other intervals? Is the area always lower for other intervals? I also wonder about the effect of choosing the starting point (for instance, instead of 20 – 40 – 60 – etc, look at 1 – 21 – 41 – 61 – etc).

It was for a practice message transposed at period 20. I also wonder about the effect of changing start points, and that is one variable for finding the correct un-transposition that can be explored.

Your observation about the shape similarity of the two graphs is interesting. Could be useful to search for untranspositions that maximize the area and the graph similarity. Not sure how to measure the similarities — perhaps you could transpose both graphs to an common average value on the Y-axis, normalize them, and then compute the root mean square distance or some other distance metric for the two graphs. Or maybe just compare slopes (e.g., how many segments go up together, and how many go down together?)

I am not sure about actual maximizing. Perhaps shape is more important, and have also considered the mean square analogy. Perhaps something similar to that could narrow down the field of untransposed messages to examine more closely.

I implemented my fragment IoC measurement but I find that it is very easy to identify false positives. First I ran a million shuffles of the Z340 to figure out the mean and standard deviation for the measurement. Then I can compute how many standard deviations away from the mean a particular untransposition’s ioc measurement is. Some of the simple untranspositions are compelling. But none of them produce any kind of spike in azdecrypt scores.

So then I took smokie27d, which is standard homophonic substitution (correct me if I’m wrong), and ran it through my transposition explorer to see if it wanders away from the "best" untransposition (which is to perform no untransposition). And it really does wander away, finding candidates untranspositions that are many standard deviations away from the expected. It may simply be that my measurement is too promiscuous when looking for repeating patterns, or I’m not doing a good job of testing for statistical significance.

I would have to check smokie27d. Let me look into it soon.

This makes me very interested in correlating the ioc measurement with other ways to detect language features in the candidate untranspositions. Possibilities include cosine similiarity, contact analysis, your periodic interval graph area, etc. I need to work on making my transposition explorer produce true positives with test ciphers.

Your experiments are exciting! I look forward to hearing more about your progress.

I intend to spend some time exploring this idea in more detail by making messages and then untransposing them correctly and incorrectly for comparison. I will look more closely at transcription skips, wrong direction, incomplete inscription rectangles, etc.

I currently don’t think that the correct approach is maximization. I think that it may be relative differences.

Yes. It is the shape of the transposed versus untransposed graph lines that is important. My theory is that if a message is untransposed correctly, then the shape will be very similar. Graph periods 1, 2, 3, etc., and periods x, 2x, 3x, etc. The shapes of the lines will be very close.

Doesn’t comparing period 1 (2,3, etc) to period 20 (40, 60, etc) already imply that the same symbols are being counted, with some extras added?

Or to put it another way – why wouldn’t the graphs be similar? Aren’t you just finding the max bigram repeats at the x20 intervals already anyway? Maybe I’m just confused about the method.