I have a question. Has anyone ever tracked to see if there are "hot spots" in the 340 where ZKD seems to find more, longer words? Has anyone ever kept track to see if long words or short phrases seem to appear on certain rows more than on other rows? Has anyone ever added a subroutine that made a list of words found and the positions of those words? I cannot imagine nobody ever having thought of or tried that. Just wondering because of the masked bigrams idea.
I would guess that more words would tend to appear in spots where there are fewer constraints (i.e., many unique cipher symbols). It would be interesting to experiment with that.
It makes me wonder about this idea: Areas of the cipher text that contain more repeated symbols are harder to fit words and phrases into. For each position in the cipher text, a measurement of this difficulty can be approximated. What would happen if the hillclimber added an additional bias to an ngram, based on the "density of repeated symbols" at (or near) the ngram’s position? For example, a 5-gram that fits into the cipher symbols "ABCDE" is likely to be much less interesting than one that fits into "ABCAC".
Yeah, it just seems to me that I have seen more words appear and disappear in certain locations as opposed to others. Row 3 and about row 16 or 17 always seem to have little phrases pop up and then disappear. With hot spots, there may also be dead zones, where word infrequently appear. It would be interesting to know if there is a pattern.
That’s a really interesting idea. With enough test ciphers, maybe there is a way to correlate the hot spots with some aspect of the cipher statistics somehow. If so, then the 340’s hot spots might tell us something about the cipher.
from jarlve’s "a good man", broken down by recognizable words where applicable, kept in the same order as his "solve". not sure if this is helpful but it was interesting to me –
a good man
cessaler
and
by the barn . . .
Thanks for that. Normally I don’t take a lot of stock in vague connections. But this is a very dark short story about the cold blooded murder of a family that has gotten into a car accident on a rural road. And it was published in 1953, same year as the Lady Doom comic. The killer’s name is Misfit. I will read through it more closely tonight; see if this has ever been referenced before. I’m not an encyclopedia of Zodiac facts, so others may spot something that I don’t. It’s a pretty quick read.
Here’s the text: http://m.learning.hccs.edu/faculty/desm … 20Find.pdf
I tried daikon’s symbol expansion idea on suspected wildcard symbols "+", "F" and "B" and came up with something that just might be a 1st stage solve or an artifact of high multiplicity.
Unfortunately, that’s often the case with high multiplicity ciphers. Because you have long sequences of non-repeating symbols, the solver tends to substitute them with whole words or even somewhat meaningful combinations of words. I’ve seen it happen too often. Only if these fragments can be put together to form proper sentences, then we have something. Another good rule of thumb — if these fragments are all shorter than 2*N, where N is the highest order of N-gram stats you are using to score the solution. I’m not saying that what you came up with is not at all a partial solve, there is still a chance that it can be cleaned up to get to the correct solution, but I just wanted to caution everyone from falling too far down the rabbit hole. 🙂
One good way to incrementally improve a partial solution to a high multiplicity cipher is to lock some of the words it came up with, thus reducing the multiplicity, and then let the solver try to figure out the rest. It is often a process of trial and errors.
EDIT: Here’s how I solved another high multiplicity cipher a while ago: http://zodiackillersite.com/viewtopic.p … 684#p37684
I’m on vacation for the next two weeks, so I don’t have access to my main computer to help out, unfortunately. This laptop can barely handle a web browser. 🙂
from jarlve’s "a good man", broken down by recognizable words where applicable, kept in the same order as his "solve". not sure if this is helpful but it was interesting to me –
a good man
cessaler
and
by the barn . . .Thanks for that. Normally I don’t take a lot of stock in vague connections. But this is a very dark short story about the cold blooded murder of a family that has gotten into a car accident on a rural road. And it was published in 1953, same year as the Lady Doom comic. The killer’s name is Misfit. I will read through it more closely tonight; see if this has ever been referenced before. I’m not an encyclopedia of Zodiac facts, so others may spot something that I don’t. It’s a pretty quick read.
Here’s the text: http://m.learning.hccs.edu/faculty/desm … 20Find.pdf
It’s a great short story. If I recall, there’s a woman in the story who thought she’d be a better person if there were someone there to shoot her every minute of her life.
Unfortunately, that’s often the case with high multiplicity ciphers. Because you have long sequences of non-repeating symbols, the solver tends to substitute them with whole words or even somewhat meaningful combinations of words. I’ve seen it happen too often. Only if these fragments can be put together to form proper sentences, then we have something. Another good rule of thumb — if these fragments are all shorter than 2*N, where N is the highest order of N-gram stats you are using to score the solution. . . . One good way to incrementally improve a partial solution to a high multiplicity cipher is to lock some of the words it came up with, thus reducing the multiplicity, and then let the solver try to figure out the rest. It is often a process of trial and errors.
Thank you for sharing that good information. I understand.
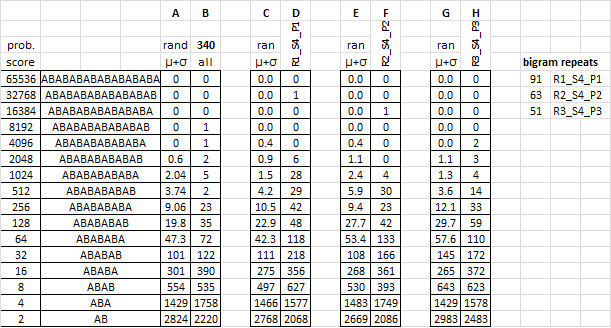
It is quiet tonight here, and I have been working on comparing R2_S4_P2, R2_S4_P2, and R2_S4_P2 with the 340. I was wondering how the cycle stats compare.
I randomized the three messages each ten times, found the mean and standard deviation for each consecutive alternation count, and then added them together.
1. Compare A, C, E and G, which gives some context to ten randomizations of the 340. When I randomized the three sample messages, I got similar results. For example, look at the differences at Row 1024. The 340 has five ABABABABABA, whereas ten randomizations can be expected to show a maximum of 2.04. That means that maybe about three are true, and two are false. R1 is not nearly random enough, and R2 and R3 are in line with the 340.
2. Look at the rows above 1024. R3 is randomized 30% and has similar long consecutive alternations compared to the 340. But R2 is randomized 20% and actually has fewer long consecutive alternations!
3. Rows 512 and below show that the 340 is more random than the sample messages; the 340 has fewer of the short consecutive alternations. All in all, the 340 stacks up a bit closer to R3 than the others, but does not match any of the sample messages with the distribution of consecutive alternations.
Roughly speaking, the 340 may be randomized somewhere around 20% to 30%. The takeaway, for me, is the context given by randomizing the sample messages. It gives a perspective on numbers of false cycles. The number of bigram repeats seems to go down when randomization is increased. R3 only has 51 bigram repeats, and the 340 has 47. My suggestion is that when working with cycles, perfect cycles may cause more bigram repeats, and randomization lowers that number. That’s my guess.
A more uniform distribution of symbols across the key letters causes more bigram repeats, and randomization lowers that number. That is what I am thinking.
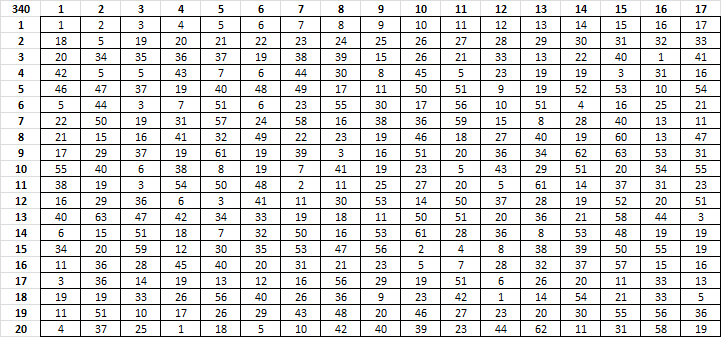
I ran R3_S$_P3 through my cycle hillclimber. Randomization was 30%. I only gathered together 17 out of 63 symbols.
I changed the hillclimber so that symbol count shows below the symbol. When there are three symbols that share the same score and roughly the same count, they are more likely to map to the same letter.
Check out:
1. Symbols 26, 27 and 33 all share the same score. They map to l and gathered together. Yet the randomized cycle was:
26,27,33,26,27,33,26,27,27,33,26,26,27,33.
2. Symbols 5, 28 and 38 all share the same count and score. They map to h and gathered together. Yet the randomized cycle was:
5,10,16,28,38,5,38,10,16,28,5,38,10,10,16,28,5,38,10,16,28,5,10,38,10,16,28,5,38,28,10. So that is interesting.
3. Symbols 29, 34 and 39. They map to i and gathered together. Yet the randomized cycle was:
2,29,34,29,39,2,34,29,29,39,39,2,34,2,29,39,2,34,29,39,2,34,29,39.
The cycle hillclimber sort of works. It’s not perfect, but with 30% randomization, I am surprised that some of these symbols gathered together so well. And a couple of low frequency letter cycles were pushed together again. v and d. So I am thinking that high scoring cycles will gather together, and low scoring cycles are pushed together, and the other symbols don’t do either. High and low extremes are more reliable as true than the scores in between.
I am thinking about someday trying to merge symbols that have the same count and score. Then run the hillclimber again to see if I can get more gathering and pushing of true cycles.
You have to excuse me but I still need to catch up with the rest of the thread.
There seems to be some sort of bug with AZdecrypt that prevents it from getting to certain solutions. I found out by moving the solving routine to another program. I did not change anything and all of a sudden it solved smokie’s purple haze message with ease and I was also able to get an easy solve on a test cipher of mine which has eluded me for months. It’s really strange and I still have to find out what exactly is the problem… and then issue forth another update.
It’s good news since I can now use the full potential of my solver.
I did a test for the 408 where one wildcard is inserted with a count of 57. After expanding the solver comes up with something that very closely resembles the plaintext of the 408. Therefore it looks realistic (as daikon stated) that we should be able to solve the 340 if it has similar wildcard counts.
ilikekillingpeopl ebecauseitissomuc hfunitismorefunth atwillingwillgame intheforderthecau semanisthemostdan gertueanamalofall tokillsomethinggi veshethemostthril lingexperencethis evenbetterchanget tingyourdocksoftw ithagilltherestpa rtofitiathaewhere dmeiwillbedeborni nparaticeandallth eihavekilledwillb ecomemyslavesiwil lnotgiveyoumaname becauseyouwilltry unexpanded: ¼ºP/_/uBºËOR¥ÐX¥B W___GyF°¼HP¹K‚ÑyÅ _Jy^u_˽ÑTÔNQyDµ£ S__¼·BPORA_º__ÌÑE Ë^L_ZJÄÒÐ_H_Wžy _+ÑG_¼KI£°ÑX_µ¤S¢ RN_IyEÌO¾ÑGBTQS·B LÄ/P·B¹X_EHMu_RRË ÃZK_Ð_£WÑ__µLMÒ¼· BPDR+_¥°_N_ÅE__ËF Z_ÐOVWIµ+Ô__Ì^R°H I¼DR¸TyÒÄÅ/¹_J__ PµM¾Ru_ºL£__EKH¥G ÒI_J˵¼¾LMÌNA£Z__ ¤_ÐËA¼·BVW+VTÔO_ ^¥SÒÌ_uÅ°_D¤GººIM NË£_ÃE/¼º__ÆA_·BV __XÑWѸF·¾Ã+¹¼A¼_ º_TµRuÃ+_ÄyÑ_^SÑW VZÅGy_E¸TyA¼º·LÔ_ expanded: ¼ºP/!/uBºËOR¥ÐX¥B W"#$GyF°¼HP¹K‚ÑyÅ %Jy^u&˽ÑTÔNQyDµ£ S'(¼·BPORA)º*,ÌÑE Ë^L-ZJÄÒÐ.H0Wžy 1+ÑG2¼KI£°ÑX3µ¤S¢ RN4IyEÌO¾ÑGBTQS·B LÄ/P·B¹X5EHMu6RRË ÃZK7Ð8£WÑ9:µLMÒ¼· BPDR+;¥°<N=ÅE>?ËF Z@ÐOVWIµ+ÔCUÌ^R°H I¼DR¸TyÒÄÅ/¹YJ[] PµM¾Ru`ºL£abEKH¥G ÒIcJ˵¼¾LMÌNA£Zde ¤fÐËA¼·BVW+VTÔOg ^¥SÒÌhuÅ°iD¤GººIM NË£jÃE/¼ºklÆAm·BV noXÑWѸF·¾Ã+¹¼A¼p ºqTµRuÃ+rÄyÑs^SÑW VZÅGytE¸TyA¼º·LÔv
I still don’t want to give up on the wildcard idea because there are some things that point in that direction. For instance the last 10 rows of the 340 (and even a bit more) having no bigrams at a period of 1 but many at 2,3,4,etc is very typical of a wildcard cipher (at least it is typical with the wildcard ciphers that smokie created). I’m also still considering the "A good man" solve since it just appeared, and the phrase likes to sit there. It’s probably insane but I think we may need to consider more wildcards…
smokie, I’d like to add your second cipher to the main post but could you add some additional information, thanks. Also, could you list your personal wildcard top 10? And what do you think of this list? Symbol numbers by appearance: 5,19,20,26,50,51.
The hobbit message kinda solves without expanding any wildcards.
inahomeintheprion
dtherelivecahobbi
snosanastydirtoge
tmilepilssswithts
eenedofformysndan
isawareslnoryetac
rowaresandwhilers
thnothinginittodi
tsignonorsieatitw
ayahobbisholeaset
hasmeananimportit
hsdamerfectlyroun
cdsorlikeaforshil
emaintespremnfmhh
ashinowelmorbrady
knowintmeetantrie
dlstsschorofsnedi
ntoatobeasameshal
lliksstunnelavery
comportabletonnel
19!/;^)2:C0*-?<EZ
'D/)@*61G)("0[#$2
]9;]X:ACLQ1?DMI*
C^<5)+26]]YJ1D0C]
)*ZHB[,U;@7S]9'":
<]NWT8)]5Z;?L*DX(
@MO?)A!9QW0<6*V]
C/:[C_1Z.291CD;B2
CY<I:[Z;@]<)"C1DJ
XS/[P#2]0;5*!]HD
/"]7)X:T%<7+[?D1C
0]'!=*@,)&D6L?;FZ
(Q][@523*">;?]/<6
)="19D*Y-@)^:U^_0
A/1ZMW)5^[V$?!BS
49;O2:D^*)K"%C81H
'5]D]](_[@;>]Z)Q<
9C[XDE#*T]=)Y/!6
5623]]CF:Z)5XG*?L
&;R+[@D#6)CE9:*5
I will post the key for the Hobbit message tonight.
At this point my favorites for wildcards are:
19 +
26 W
20 B
51 F
5 q (the backward’s P; is that just a small "p" in your lingo?)
In that order.
I was thinking about wildcards this morning. There are just so many symbols crammed into that thing, and so many of them are low count. One possibility is 19 and various other low count symbols. So, yes, I will start checking tonight for lower count symbols.
Jarlve, you may be shocked to see this, but I have found yet another way to organize symbol cycle statistics.
The following other symbols are not in any cycles with high statistical significance, some of them because of low count. I have verified this by looking at them individually.
18 count: 5
1 count: 4
2 count: 3
9 count: 3
24 count: 2
35 count: 2
45 count: 2
49 count: 2
52 count: 2
57 count: 2
59 count: 2
That’s a total count of 29. See also the 6th post at: viewtopic.php?f=81&t=2617&start=80, where I discuss my analysis for the other symbols that you were talking about today. Unless Zodiac cycled wildcards, this is my best interpretation to date.
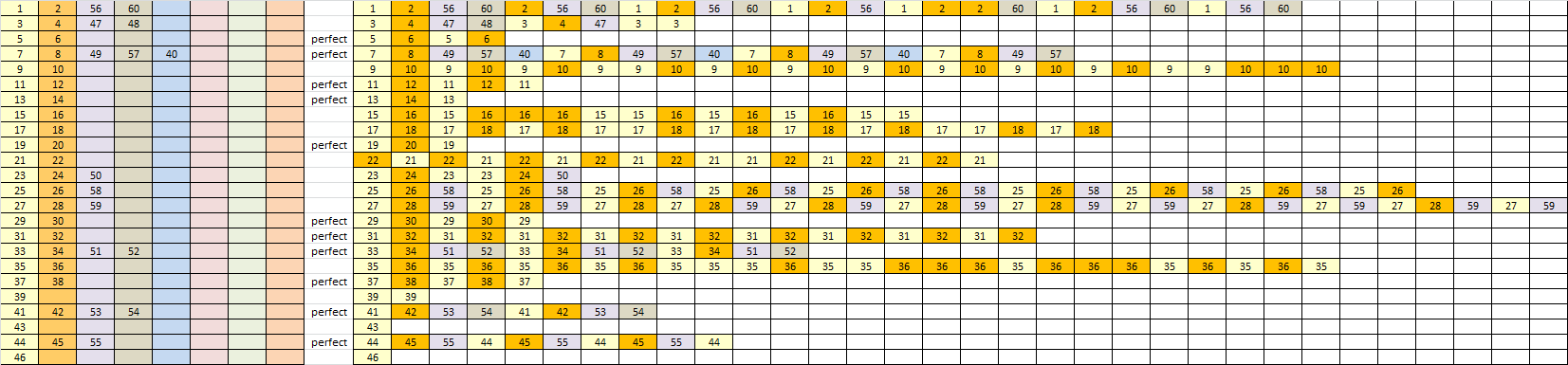
Here is my grid, just to make sure we are on the same page. If you can get a decent solution by expanding symbols, and some of the expanded symbols turn out to be the same letter, we can always merge them back together for proof that there is no other way to find the same solution.
And here is the Hobbit key:
A 1 2 56 60
B 3 4 47 48
C 5 6
D 7 8 49 57 40
E 9 10
F 11 12
G 13 14
H 15 16
I 17 18
J
K 19 20
L 21 22
M 23 24 50
N 25 26 58
O 27 28 59
P 29 30
Q
R 31 32
S 33 34 51 52
T 35 36
U 37 38
V 39
W 41 42 53 54
X 43
Y 44 45 55
Z 46
Here is the message before bigram masking:
17 25 1 15 27 21 9 18 26 35 16 10 13 31 28 37 58
7 36 15 9 32 10 22 17 39 9 8 2 16 59 3 4 18
35 25 27 36 56 26 60 33 35 44 49 17 31 36 45 41 10
35 15 28 21 9 11 18 22 21 10 57 42 17 36 16 35 15
9 10 58 40 34 59 12 53 27 32 23 51 1 25 7 2 26
28 59 46 55 52 24 9 22 21 58 27 31 44 10 36 56 8
32 45 47 60 31 9 33 1 25 49 55 16 28 22 10 54 18
35 15 26 59 36 16 17 58 14 18 25 17 35 36 27 34 18
35 57 28 41 26 59 58 27 32 36 28 9 2 35 18 36 42
56 51 60 15 59 48 3 18 35 16 27 21 10 1 25 40 36
15 2 35 50 9 56 26 52 5 28 23 11 59 31 36 17 35
16 60 7 1 29 9 32 12 9 6 36 22 44 31 27 38 58
8 49 28 59 32 21 18 19 10 2 30 27 31 35 15 28 22
9 29 56 17 25 36 10 57 13 32 9 10 26 53 18 35 16
60 33 15 17 58 45 55 9 21 22 59 54 4 31 1 34 51
20 25 27 47 18 26 36 16 10 9 43 60 5 35 24 17 40
7 21 10 36 15 9 8 28 59 32 27 29 10 58 9 49 28
25 35 59 56 36 37 48 10 52 16 60 29 9 57 15 1 22
21 22 18 19 10 2 35 38 26 58 9 22 56 39 10 31 44
6 27 24 11 28 32 36 60 3 22 9 35 37 25 26 10 21
Here is the message after bigram masking (masking only one of the two bigram repeat symbols):
17 25 1 15 27 62 9 18 26 35 16 10 13 31 28 37 58
7 36 15 9 32 10 22 17 39 9 8 2 16 59 3 4 18
61 25 27 61 56 26 60 33 35 44 49 17 31 36 45 41 10
35 62 28 21 9 11 18 22 61 61 57 42 17 36 16 35 61
9 10 58 40 34 59 12 53 27 32 23 51 61 25 7 2 26
28 61 46 55 52 24 9 61 21 58 27 31 44 10 36 56 8
32 45 47 60 31 9 33 1 25 49 55 16 28 22 10 54 61
35 15 26 59 35 63 17 58 14 18 25 17 35 36 27 34 18
35 57 28 41 26 59 58 27 32 61 28 9 2 35 17 36 42
56 51 60 15 59 48 3 18 61 16 27 21 10 1 61 40 36
15 2 61 23 9 56 26 52 5 28 23 11 59 31 36 17 35
16 61 7 1 29 10 32 12 9 6 36 22 44 31 27 38 58
8 49 61 59 32 21 18 19 10 2 30 27 31 61 15 28 22
9 29 2 17 25 36 10 57 13 32 9 62 26 53 62 63 16
60 33 15 17 58 45 55 9 21 62 59 54 4 31 1 34 51
20 25 27 47 18 26 36 62 10 9 43 2 5 35 24 17 40
7 21 61 36 61 61 8 63 59 32 27 30 61 58 9 49 28
25 35 59 56 36 37 3 10 52 61 60 29 9 57 15 1 22
21 22 18 19 61 61 35 38 26 58 9 21 56 39 10 31 44
6 27 50 11 59 32 36 60 3 22 9 35 37 25 26 10 21
And here is the solution:
I n a h o l e i n t h e g r o u n
d t h e r e l i v e d a h o b b i
t N o t a n a s t y d i r t y w e
t h o l e f i l l e d w i t h t h
e e n d s o f w o r m s a n d a n
o o z y s m e l l n o r y e t a d
r y b a r e s a n d y h o l e w i
t h n o t h i n g i n i t t o s i
t d o w n o n o r t o e a t i t w
a s a h o b b i t h o l e a n d t
h a t m e a n s c o m f o r t I t
h a d a p e r f e c t l y r o u n
d d o o r l i k e a p o r t h o l
e p a i n t e d g r e e n w i t h
a s h i n y y e l l o w b r a s s
k n o b i n t h e e x a c t m i d
d l e T h e d o o r o p e n e d o
n t o a t u b e s h a p e d h a l
l l i k e a t u n n e l a v e r y
c o m f o r t a b l e t u n n e l
EDIT: Below are the cycles, many of which are perfect. There are no high count 1:1 substitutes. The wildcards symbols that I used for masking bigram repeats were 61, 62 and 63.
Yeah, it just seems to me that I have seen more words appear and disappear in certain locations as opposed to others. Row 3 and about row 16 or 17 always seem to have little phrases pop up and then disappear. With hot spots, there may also be dead zones, where word infrequently appear. It would be interesting to know if there is a pattern.
That’s a really interesting idea. With enough test ciphers, maybe there is a way to correlate the hot spots with some aspect of the cipher statistics somehow. If so, then the 340’s hot spots might tell us something about the cipher.
These are top solves for the 340 from AZdecrypt096 together with a map that indicate hotspots and deadzones by giving each square in the cipher grid a color according to the score of the 5-gram (brighter is better). Because 5-grams are used the last 4 squares of the grid are unscored.
It’s the first time I did this and find it interesting that the 2nd line scores so low.
Edit: please go to the next page to see the new and improved pictures.
Ioc target weight 2:
gyhiscentofurnasm ostelliaarmdeiaco edlantocarlorlegi nsspectingsitthas sunteramfortthdoe sthercisimporisal lotanalsoabanderf lasicalitsomethru mentitchsreadymda seconteitispereds otheoryfamesinnai seachifiondndther emundltoforeallth caroecosdidandrtt debuildupyinocost fadgeealisedcnnas hantrumpetrcrefor ttorperatingnelos fromrepresmieispa inagosonecityfalt
http://i61.tinypic.com/m8dvgn.png
Ioc target weight 0:
gshiscentopernatm estelsilarldeiavo edvantocarlorsegi nsspectingsitthat sunterimporttheof sthercisimporital sotablytoacanderp lativisitseletoru mentatchtreadysea seconteitispereds othforspalesannai teachipionendther esundsteporealyth careevoteadanertt deceiveupsinocost padgeealisedvnbat hantrespetrcrepor ttorperatingnflos promrepreslieispa inagesonecitypayt
http://i60.tinypic.com/2w56l2d.png
Hmm, this makes me think it is best to place wildcards very evenly throughout the cipher, so it masks/destroys as many higher-order N-grams as possible, so that ZKD/AZD have nothing reliable to use to score the solution. Every 4th or 5th symbol would be ideal. I highly doubt Z would realize that though. I think he would be much more likely preoccupied with masking bigrams, to hide "KILL", etc., so that it won’t be solved as easily as Z408.
Yes, that’s a sure way to let the solvers run into problems and it’s why columnar transposition is so difficult to crack. I believe back in the time they used computer assisted word slides. For instance the word killing was placed from character one (sliding to the end) and all corresponding symbols were given the appropiate letters and they looked for similarities. I think the Zodiac could have known about this and placing wildcards uniformly throughout the cipher would likely corrupt the word slides.
I marked the symbols that I strongly suspect as being wildcards in green, the weaker candidates in grey. So nineteen out of 46 repeats include symbols 19 or 20. Let’s say, hypothetically, that Zodiac created these 19 repeats during the masking process. So then take these out for a minute, and we have 46 – 19 = 27 bigram repeats that were created by the cipher’s cycle step and not masked. Total count of symbols 19 and 20 = 36. With 36 symbols, and masking bigram repeats with only one symbol per repeat, we can mask 72 repeats. 72 + 27 = 99 bigrams to start with. Isn’t that about what we should have without the mystery step?
It’s a disturbing quality of the 340, allot of patterns, bigrams are indeed correlated with the "+" symbol. I have done some work and I believe that in general it looks convincing that the message is written horizontally. Though when the "+" symbol is removed from the cipher I’m not so sure anymore, but *it is* a part of the cipher.
I’m on vacation for the next two weeks, so I don’t have access to my main computer to help out, unfortunately. This laptop can barely handle a web browser.

Have a nice one!
Jarlve, you may be shocked to see this, but I have found yet another way to organize symbol cycle statistics.
The picture now shows the score per symbol? I have exact the same grid, we are on the same page. What do you think about symbols 7 and 54? If the wildcard hypothesis will turn out to be actual he could not have been an amateur imo. Whatever was done, it was hidden very well. Both wildcard ciphers you created have telltale signs floating around, the Zodiac 340 not so much.
Could you give some specific information about the hobbit cipher also, perfect cycles? 1:1 substitutes? wildcard symbols number? Thanks!
It’s the first time I did this and find it interesting that the 2nd line scores so low.
Interesting! How do they compare to hotspots of 340-character ciphers with known solutions? And the 408?