Jarlve, I do appreciate your answers as they really get it to the point. Please, for a minute, let’s go a little bit deeper into the issue of how your examine tool can help to solve the cipher. Please do also read it carefully and do not hesitate to ask, if any questions may occur:

1.) The complexity of the 340 is higher than that of the 408. The cleartext-to-homophone ratio is – unqually distributed – 5.397 compared to 7.418, making the 340 much harder to crack.
2.) A similar complexity ratio of the 340 would require to ‘guess’ 18 symbols correctly, thus leading to 340/45 = 7.555
3.) The 340 has 63^26 variations, thus 60,653,000,000,000,000,000,000,000,000,000,000,000,000,000,000 or 6.06E+46. The examine tool can handle about 100,000,000 variations in one run.
4.) Donald Gene and Bettye June Harden had cracked the 408 by applying certain cipher structures (‘kill’, ‘I like killing’)
5.) Such cipher structures do exist in the 340, too. Double letters, two trigrams appearing twice each (although additional ones might be hidden behind different homophones), etc.
6.) Based on the number of homophones Z had used (according to a separate (!) frequency table), Bernoulli formula shows that the odds for + being an ‘L’ is 71.1% (with ‘S’ being the second highest with a value of 2.3%). Other letters either are expected to have more than 3 homophones (e.g. ‘S’, leading to the low value) or are not expected to appear that often as a double letter (e.g. ‘VV’)

Therefore I do believe that due to the amount of variations (6 Billions^5 or 6.06E+46), such existing cipher structures should be considered when using the examine tool. This step may enable the examine tool to crack the cipher, which is currently not yet the case. Such considerations of cipher structures may be e.g.:

– considering e.g. + being an ‘L’ due to Bernoulli (or trying + to be an L, S, R,…)
– considering frequent trigrams, e.g. expectations >1 for the two at least twice reappearing trigrams (> expected frequency of trigrams)
– considering related structures, e.g. a vowel previous to ‘++’ or two frequent trigrams in combination as being a 5-gram (line 13, row 9)

otherwise the Examine tool possibly would have to run for a very long time..

In addition to that: Hillclimb method is the correct one, however regularly locks in to a local optima (value of ~13,000), while we are actually trying to force it to the global optima (the correct or nearly-correct solution). To force hill climb / examine tool doing so, it imo is necessary to configure additional assumptions to reduce the cipher’s complexity. This can be done, preferrably according to the cipher structure, by various methods such as but not limited to:

a.) Assuming + being an ‘L’ (or R, S,..)
b.) Assuming the first symbol of the cipher to be a vowel (or a consonant)
c.) Considering the two frequent trigrams to be statistically ‘frequent’ ones (therefore not being e.g. ‘ZZG’ or ‘GQM’ but rather ‘THE’ or ‘ERE’)
d.) Considering the 5-gram in line 13, row 9, being a combination of two of such frequent trigrams (‘THERE’ rather than ‘ZZGQM’)
e.) Considering a frequent symbol (e.g. the reversed P symbol) to not be a non-frequent letter (e.g. X, Q, Y would most likely not appear with a frequency of 5% in the cipher)
f.) Considering the bigram appearing three times in the cipher to be a frequent bigram, too.

Therefore the examine tool ideally would be adaptable so that certain symbols (or symbol combinations, e.g. trigrams) can exclude or include certain cleartext letters (e.g. exclude X, Y, Q for the reverse P symbol; using a list of frequent cleartext trigrams for the repeating and therefore frequent, too, cipher trigrams).

I would like to give an example of how I’d love to apply the Examine tool:

1. Setting the + symbol (e.g. ‘L’)
2. Setting the trigrams to a list of frequent trigrams (e.g. all trigrams that would appear 1.5 in a 340 cipher [44 per 10,000])
3. EASIER: Setting the 5-gram (line 13, row 9) to a list of (possibly frequent) 5-grams consisting of two frequent trigrams (‘THERE’, ‘THANT’, ‘WHICH’,..)
4. Setting the bigram in line one to a list of frequent bigrams (‘EN’, ‘TH’,..)
5. Excluding certain letters for certain symbols (e.g. X, Y, Q for the reverse P symbol)
6. RUN the examine tool and let it then check out some 100,000,000 variations..

It is obvious that especially step no. 3 is dramatically reducing the amount of variations. My expectation is that, considering this approach, the examine tool should become able to crack the 340. As I said, however, I do believe that it is a necessary step to solve it (if not accidentially).

Regarding your point that such modification would ‘interrupt’ the process:
The process is indeed influenced in a negative way: The solving process is now definitely slower than before (is it really?). The program can’t just use any 5-gram to be placed in, but has to use one that e.g. has one L on the third position and one T on the fifth position. But this exactly is the solving process we actually need. The other two methods, trying all variations or solving the cipher like a newspaper puzzle, both don’t work out. The first one because of the huge amount of variations (too high..), the second one because there is a lack of cipher structures such as more 4-grams or trigrams.

By using millions of variations under the pre-condition of existing cipher structures in combination with certain frequencies, the example tool should become successful.

Criticism:

Q: What if the reappearing trigrams or the 5-gram are not among the e.g. 2,000 most frequent ones?
A: Not very likely but tThere is the possibility to try the second most frequent 2,000 trigrams/5-grams, too. It will end up that the 5-gram is not ZZDZQ.

Q: What if the + is not an ‘L’? Or the reverse P symbol in fact is a Y?
A: Exclusions and inclusions could be done by anyone as he/she prefers. E.g. trying a certain group of letters to be excluded for the reverse P, then a second group of letters.

Q: What if the homophones are not distributed according a certain frequency table?
A: Nevertheless the preconditions helps to reduce the amount of variations to be checked through.

Q: What if the cipher then still cannot be solved?
A: Do not think so. But additional steps are possible, e.g. focussing on other cipher structures. Or it may even be not solvable, but I clearly doubt it.

My estimation is that the method described above leads to a reduction of the present 6 billion^5 or 6.06E+46 variations to approximately

63
minus 5 (5-gram list)
minus 2 (bigram list)
minus 1 (+ symbol)
minus 1 (e.g. vowel before plus symbol)
minus 1 (exclusion of revers P letters)

leading to an overall of 53^26 variations (still to be multiplied with the number of 5-grams, bigrams etc. used – which can actually be one by trying one run after another). This still is a number, but the complexity ratio has then increased to 6.415 (which is good, meaning a reuced complexity) instead of 5.397. It is therefore at least closer to a value of 7.418 (408 cipher), latter one has been proven to be solvable by methods of computation in the past.

In addition to that, the most frequent variations are covered instead of rare ones, too. This one I like most. A comparison of the amount of variations before and after the modification shows the advantage:

340 (unsolved):
63^26=
6.06E+46 variations

408 (solved):
55^26=
1.78E+45 variations

340 with modification:
53^26=
6.78E+44 variations

So the modifications in fact are leading to a 340 that has even less variations to be hill-climbed than the – already solvable – 408.

Again, I most appreciate your work and guess you therefore will be the first person to become able to read the cleartext. Would love if you share this idea (and the solution).

QT

QT-

While I would NEVER say that ZKDecrypto is a panacea, or a great solver, doesn’t it do what you ask? It seems, in a way, that we are asking programmers to do the same thing over and over again.

-glurk

QT-

While I would NEVER say that ZKDecrypto is a panacea, or a great solver, doesn’t it do what you ask? It seems, in a way, that we are asking programmers to do the same thing over and over again.

-glurk

Think it actually is a great solving tool, but a bit slow.

The main point is that it is hard to try one 5-gram after another in combination with let’s say 40 frequent bigrams one after another. Although this would indeed work. With only 200 5-grams, however, it would mean to 4,000 times select seven symbols. Then run it with the slow program, not being sure that it finds the correct solution on the first run. I actually tried some, but it ends up in quite a lot of work.

But in generally it does, except that you can’t lay a complete list of n-grams behind these specific cipher fractions.

Below you find a pic on which cipher the examine tool would run if only three steps were taken as a pre-condition: The leading + symbol, the 5-gram (consisting of frequent trigrams) and the bigrams (being frequent, too). It should be obvious that based on this cipher structure running through 100,000,000 variations makes way more sense:

If that doesn’t do it, by the way, there still is the possibility to reduce the 5-grams loaded (NOT [updated] IoFBc but the ones doing the hill climb work, the corpora). Just to let the solver be faster and using a more frequent corpora, even if only parts of the cipher might be solved.

Update:
Bigrams expected to appear at least 1.5 times in 340-2=338 trigrams:
th 1.52
he 1.28
in 0.94
er 0.94
an 0.82
re 0.68
nd 0.63
at 0.59
on 0.57
nt 0.56
ha 0.56
es 0.56
st 0.55
en 0.55
ed 0.53
to 0.52
it 0.50
ou 0.50
ea 0.47
hi 0.46
is 0.46

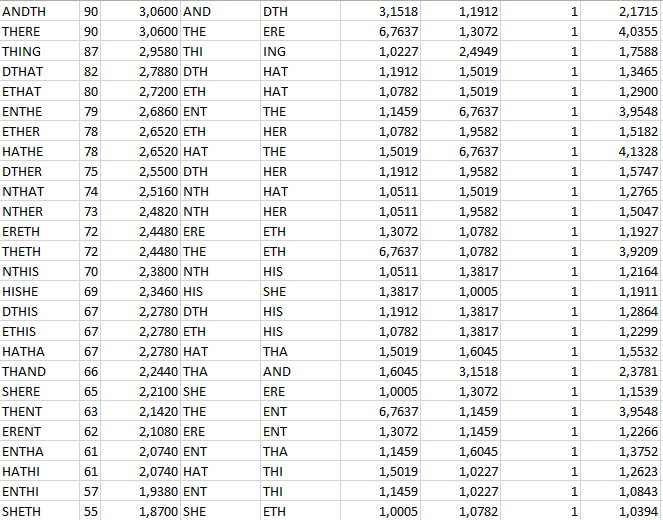
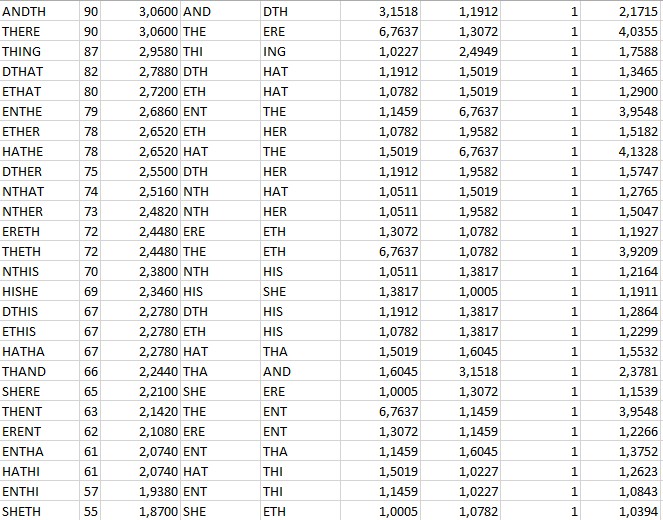
(Corrected) list of 5-grams consisting of two trigrams (IoFBc) with both trigrams appearing at least >1 in the 340 (updated: out of the 263,342 most frequent 5-grams):

ANDTH
THERE
THING
DTHAT
ETHAT
ENTHE
ETHER
HATHE
DTHER
NTHAT
NTHER
ERETH
THETH
NTHIS
HISHE
DTHIS
ETHIS
HATHA
THAND
SHERE
THENT
ERENT
ENTHA
HATHI
ENTHI
SHETH
ERERE
SHENT

Combining these with the + symbol leads to the structure in the picture above. Using more bigrams and 5-grams lead to a bigger sample, although statistically this would be an outlier.

Currently I do combine all those above with three additional symbols,

and

to try to cross-check it with text fractions in line 17/18 of the cipher..works quite well, but still a variety of potential solutions and have not found the final one yet. LETINSTALLTIDBIT or LETINSTALLTINYIT is such potential text fraction, so far (based on the n-gram ‘SHENT’).

QT

@Quicktrader, I’m not sure the search space argument holds much weight in relation to the 340. AZdecrypt has solved a 618 character cipher with 221 symbols (try 221^26) and longer ciphers with even more symbols for that matter.

I would like to give an example of how I’d love to apply the Examine tool:

1. Setting the + symbol (e.g. ‘L’)
2. Setting the trigrams to a list of frequent trigrams (e.g. all trigrams that would appear 1.5 in a 340 cipher [44 per 10,000])
3. EASIER: Setting the 5-gram (line 13, row 9) to a list of (possibly frequent) 5-grams consisting of two frequent trigrams (‘THERE’, ‘THANT’, ‘WHICH’,..)
4. Setting the bigram in line one to a list of frequent bigrams (‘EN’, ‘TH’,..)
5. Excluding certain letters for certain symbols (e.g. X, Y, Q for the reverse P symbol)
6. RUN the examine tool and let it then check out some 100,000,000 variations..

1) This functionality is already available (locking symbols to letters).

2,3,4) The way I’d like to add the n-gram functionality is that you select a symbol and then press a key which prompts you which n-gram size you like to use. If you for instance choose 4-gram the solver will then lock the symbol and the other 3 symbols that follow it to use a secondary 4-gram list. So that it will not change any of the involved symbols individually, but rather as a whole, picking a random 4-gram from the secondary list.

5) The way I’d like to add the letter excluding functionality is that you select a symbol and then press a key which prompts you to enter a string of letters the symbol can use. For instance you enter "aeiou" or "etaoinshrdlu" and if you leave it empty it’ll revert to "abcde…".

Does that seem okay for you?

@Quicktrader, I’m not sure the search space argument holds much weight in relation to the 340. AZdecrypt has solved a 618 character cipher with 221 symbols (try 221^26) and longer ciphers with even more symbols for that matter.

I would like to give an example of how I’d love to apply the Examine tool:

1. Setting the + symbol (e.g. ‘L’)
2. Setting the trigrams to a list of frequent trigrams (e.g. all trigrams that would appear 1.5 in a 340 cipher [44 per 10,000])
3. EASIER: Setting the 5-gram (line 13, row 9) to a list of (possibly frequent) 5-grams consisting of two frequent trigrams (‘THERE’, ‘THANT’, ‘WHICH’,..)
4. Setting the bigram in line one to a list of frequent bigrams (‘EN’, ‘TH’,..)
5. Excluding certain letters for certain symbols (e.g. X, Y, Q for the reverse P symbol)
6. RUN the examine tool and let it then check out some 100,000,000 variations..

1) This functionality is already available (locking symbols to letters).

2,3,4) The way I’d like to add the n-gram functionality is that you select a symbol and then press a key which prompts you which n-gram size you like to use. If you for instance choose 4-gram the solver will then lock the symbol and the other 3 symbols that follow it to use a secondary 4-gram list. So that it will not change any of the involved symbols individually, but rather as a whole, picking a random 4-gram from the secondary list.

5) The way I’d like to add the letter excluding functionality is that you select a symbol and then press a key which prompts you to enter a string of letters the symbol can use. For instance you enter "aeiou" or "etaoinshrdlu" and if you leave it empty it’ll revert to "abcde…".

Does that seem okay for you?

Ok? This is perfect .

Please rethink the ‘random’ selection of n-grams. This is crucial because it might be more useful to back it with a specific (e.g.) 5-gram list. The one I use is a combination of

a.) trigrams sorted according to a specific frequency value and
b.) the 5-grams sorted according to their own frequency, too:

In this file I first set the precondition that both trigrams appear at least e.g. 1.5 times in the cipher. This value may be modified, e.g. to a value of 1.0 only, too (as shown in the picture).

Setting up such precondition leads to a marker (‘1’) according to which I sort first, thus eliminating all other (statistically outlier) 5-grams consisting of various non-frequent trigrams. After that, however, I do sort the 5-grams, too, according to their own frequency. This list may finally be checked ‘one-after-another’. If your tool selects any n-gram randomly, chances are very high (>99.95%) that the tool chooses any out of e.g. 263,320 5-grams. The ones consisting of frequent trigrams (~150 or so} would not really be checked first although exactly those do fulfill the criteria of ‘consisting out of two frequent trigrams’.

Thinks for your interest into this issue

QT

@Quicktrader,

The way I see it is that the solver uses another n-gram list for the n-grams you wish to mark. You supply this list yourself so you can do whatever you want. For instance I make a secondary 5-gram list with entries: ZODIAC, OFTHE, ABCDE. The solver will select a 5-gram from that list randomly to the 5-grams you marked in the cipher everytime it makes a change. So eventually it’ll end up with the best fitting 5-gram for that piece of ciphertext. Is that okay?

Download AZdecrypt099.

– About 30% faster!
– Changed some of the terminology to better reflect what is going on. Changed "iterations" to "random restarts" and "keys per iterations" to "iterations per restart".
– Added a new solver mode, a QoL addition for just trying to solve one cipher.
– Some minor bug fixes.

Explanation of the new solver mode (progressive).

In the upper right corner there is a new box called Solver mode, normal is as the program has always been, a solver for many ciphers. When using the progressive mode the program will only read in the first cipher it encounters in the range of files you have specified (1.txt etc). The settings "random restarts" and "iterations per restarts" are still used.

To give an example, lets say you keep everything at default, change the solver mode to progressive and click on start processing. The solver will then process 10 (equal to the number of random restarts per cipher) copies of your ciphers at 500.000 iterations per random restart (equal to the setting you used). When these are processed the solver will then double the amount of iterations per random restart (from 500.000 to 1.000.000) and process another 10 copies. This continues until you end the program with the "x" key.

I’m not entirely sure yet what is optimal but I’d say you want to use at least 10 random restarts per cipher and 30 may be better. It depends on the cipher. The file output format includes the number of iterations used for each cipher in millions.

Example: 23274_654_132_32m.txt (32 million iterations).

Awesome progress! And I finally understand what you mean by "iterations". I suspected it was the same as a random restart, but now I know. 🙂

By the way, how do you handle "keys per iteration" (old name) / "iterations per restart" (new name)? What I mean is, you use Simulated Annealing, right? So you have a starting temperature, and then you reduce it by a small amount (delta) for each iteration. When increasing the number of iterations per restart, do you reduce the delta accordingly and always end up with the same final temperature, or do you keep the same delta, but let it run more iterations, so you end up with lower final temperature? Or is it both?

The reason I ask, is that in my experiments, I found that there is a sweet spot for the temperature when you get to the correct solution. And there is almost no reason to go lower as the algorithm becomes a purely greedy search (no exploration) past a certain temperature, which means if it missed the correct solution, it will never find it no matter how many more iterations it does. So if you are keeping the same delta and letting it do more iterations at lower temperatures, it’s probably not ideal. It is much better to let it do more restarts instead. At least that’s how my solver seems to behave. In any case, your solver might work differently, so I encourage you to test a bunch of different ciphers and record the temperature of when it gets to the correct solution, and use the minimum value as the final temperature in the algorithm. When I did the same test with my solver I was surprised to learn that I was using too low value for the final temp, so I was wasting a lot of time unnecessarily.

Thanks daikon,

I know what you mean and are aware of the sweet spot. The temperature is reset for every restart. As you indicate, it is possible to find highly optimized values (sweet spot) for one or a even a bunch of ciphers but more difficult ciphers could (and do) have a lower sweet spot. That being said my solver does drop quite low and drops a bit lower as the iterations go up.

The temperature range is optimized (not only by score) to a wide variety of ciphers (multiplicities). I usually run 1000 iterarions of 40 different ciphers (some of them are partials) and then look at the recovery rate for every cipher and the average score for all the ciphers.

I have been thinking about a more adapative temperature system since that could be a very big improvement.

Hows your solver coming along? Any plans for a release or working on a GPU version?

The temperature range is optimized (not only by score) to a wide variety of ciphers (multiplicities). I usually run 1000 iterarions of 40 different ciphers (some of them are partials) and then look at the recovery rate for every cipher and the average score for all the ciphers.

I need to that still. I have about a dozen ciphers that I test my solver with, and probably need more variety. I just run 10 restarts for each cipher, and if each gets solved at least a couple of times, I’m happy. I need to do a proper optimization test: change each parameter in the algorithm, run a number of tests, and then optimize for the percentage of correct solutions.

I have been thinking about a more adapative temperature system since that could be a very big improvement.

I’ve played with the number of iterations per temperature, and starting/final temperatures a lot. I don’t keep track of number of overall iterations, I use the final temperature as the "out" condition. And I’ve found that the number of iterations per each step (I do 50-100 iterations per each temperature, before lowering it) and the final temperature are pretty stable parameters. Once you find the values that work, there is very little improvement in increasing the iterations per step, or lowering the final temperature. For harder ciphers, it is always better to do more restarts instead. But the starting temperature proved to be tricky. Some ciphers get solutions at higher temperatures, so you need to keep it pretty high, and some at lower temperatures. I’ve even considered using a similar "progressive" system that you came up with: start with lower starting temperature, and then gradually raise it with each restart. For now, I just keep it high. It takes more time for each restart, but at least it covers all possible cases.

Hows your solver coming along? Any plans for a release or working on a GPU version?

I’m stuck, with no new ideas. 🙂 I am planning to work on an OpenCL (GPU) version next. I even got a new graphics card with 2048 cores. It has a slower clock rate than CPU (~1Ghz vs ~4Ghz), but I think it can do more instructions per cycle, and the memory is much faster (about 10x regular RAM). So it should be able to handle about 1000 times more ciphers vs CPU. Well, 250 times, since I have 4 CPU cores. But the problem is, I’m not sure where to throw all this power yet. It’s still not enough to handle 17! transpositions in a reasonable time. I keep working on a hill-climber/SA algorithm that does both transpositions and substitutions, but it has yet to solve even a simplest test. It can solve just transpositions, without substitutions. And subscriptions alone, of course. But doing both proves to be tricky.

Meanwhile, my main computer keeps churning through the wildcards idea. I set it to do all possible combinations of 3 wildcards out of top 10 symbols, forwards and in reverse. It’s been at it for 3 weeks now. Nothing to report. I’ll let it keep running, even though it went through all permutations 7 times already. But I don’t have any better ideas at the time, and it could be a matter of luck with wildcards, as you end up working with very high multiplicity ciphers.

Meanwhile, my main computer keeps churning through the wildcards idea. I set it to do all possible combinations of 3 wildcards out of top 10 symbols, forwards and in reverse. It’s been at it for 3 weeks now. Nothing to report. I’ll let it keep running, even though it went through all permutations 7 times already. But I don’t have any better ideas at the time, and it could be a matter of luck with wildcards, as you end up working with very high multiplicity ciphers.

I’m running a somewhat similar experiment. I’ve made a number of expanded versions of the 340. The 1st one only has the highest count symbol expanded, the 2nd one the 2 highest count symbols, the 3rd one the 3 highest and so on… When they are all done I plan to look for similarities between the versions. Solving an expanded cipher is easier, so higher multiplicities can be attempted.

Just to clarify, what do you mean by "expanded"? Same idea as we had for wildcards? I.e. replace the symbol with a new unique one for each occurrence?

Yes, that was your idea and terminology actually.

You guys are always coming up with new ideas, so I can never be sure if you are talking about the same thing as before, or if it’s already something completely new. 🙂

Hows your solver coming along? Any plans for a release or working on a GPU version?

So, I’ve finally implemented an OpenCL version of my solver running on GPU. It turned out to be quite disappointing. I didn’t get the speed-up I was hoping for. Not even close. It was kind of fun rewriting everything into the shortest possible C code. Turned out you only need about 100 lines of code for the innermost loop (excluding all initializations, loading of the N-gram table, etc. etc.). The normal version of my solver runs about half a million iterations per second on the CPU. So, for a 4-core CPU, you get around 2M iterations/sec (4 "restarts" in parallel). The new OpenCL/GPU version runs about 4M iterations/sec on a 2000-core GPU.

I thought it was a 2000-core GPU, but turns out the GPU cores are not quite the same as CPU cores. In reality, it’s more like 16 cores, that can run 32 threads in parallel, each of which can process 4 bytes/ints/floats at the same time. Which translates to 16*32*4 = 2048 sort-of "cores". But not quite. They just like to throw those "core" numbers around, as it sounds impressive. Nothing more than a marketing hype. I thought maybe I screwed up and when I was rewriting the code for OpenCL, I made it much slower somehow. Which is possible, but kind of unlikely, as it’s just 100 lines and I was staring at them for several days now, trying to optimize the hell out of them. Also, modern CPUs (Core i3/i5/i7) can actually run OpenCL code as well, and when I run the OpenCL version of the solver on the CPU, I get 2.5M iterations/sec. Which actually improves the old, non-OpenCL, plain-CPU solver numbers (2M iterations/sec) a bit, so I think it’s not the implementation, but the GPU architecture that’s the problem.

One reason, GPUs are optimized for sequential access to memory. They access memory in 128-bit chunks. So if you need to read 1 byte, it actually has to load a 16-byte "line" that contains the byte you need. Which is good if you need to read 4 floats, or 4 integers, or 4x 32-bit pixels in a texture, but not if you only need 1 byte. So it ends up being about 16 times as slow, compared to normal RAM. And then there are 16K banks, for which I still haven’t quite grasped the rules for optimal access. But the worst of all, I think, is the size of the cache. Even on my pretty high-end card it’s only 48K, which is shared with all threads. So you end up with just 24 *bytes* per thread (if you are running 2000 of them in parallel). It’s not even enough to fit Z340 ciphertext that you are trying to solve, so it’s like not having any cache at all. Modern CPUs usually have at least 1Mb of cache per core. So, all in all, it seems that the cipher cracking is not the type of task that’s well suited for OpenCL/GPU. I’ll keep working on it to see if I can get a better performance out of it, but at this point, it doesn’t seem to be much of an improvement over plain old CPU. We’ll have to find a different way to get through all 17! possible transpositions for Z340. 🙂