Hello all,

Here is a modest attempt to advance a little in the understanding of the famous Z32 cipher of the Zodiac.

As you know, this cipher was supposed to reveal the location of a bomb intended to "anilate a full school buss" and was accompanied by a map which should help in its resolution.

A full decryption of this code is made nearly impossible due to its short length : it only has 32 characters, of which only 3 are repeated. Unlike the Z408 or Z340 ciphers, and if the Z32 is indeed based on an homophonic substitution method, it is almost impossible to detect patterns and therefore to find the right solution.

The starting idea here is very simple : build a large number of plausibles solutions and test them to identify those which satisfy the constraints derived from the following hypothesis :

This is a homophonic substitution cipher, written from left to right and from top to bottom, without words written backwards or misspellings (which is not the case in the other decrypted codes, but we can hope that the short length of the Z32 cipher protects us from these difficulties ?).

This code contains two pieces of information, as specified by the Zodiac in a letter sent one month after sending the original cipher : an angle (called "RADIANS") and a distance (measured in “INCHES”). From the map accompanying the Z32, it is clear that the origin of the coordinates must be the Mount Diablo.

Regarding the angle, the drawing on the map suggests that it is measured like on a clock : it is highly probable that the term RADIANS does not refer to true radians measured with the pi number (who measures angles with fractions of PI in the real world ?). The angle here is expected to be measured in hours and possibly minutes. Finally, it should be noted that the reference of this angle is indicated as being the magnetic north which, in the San Francisco region and in 1970, deviates by 17° from the geographic north.

Regarding the distance, we expect a measurement in inches, in the form of an integer and a fractionnal part (1/16, 1/8, 3/16, …).

The solution must obviously contains 32 letters. Even if this is not certain, we can think that there is a separation in the solution : a first part with 17 characters, then and a second on with 15, corresponding to each of the two lines of the cipher. The fact that the Zodiac didn’t choose to write 2 lines of 16 characters could indicate that one line concerns the angle and the other one the distance. But this is a fragile hypothesis and I didn’t use it in the following process.

And the most important point : we have three repeated letters: C, Delta and O, that the solution must respect.

These last two constraints will help us to find what messages the cipher could contain. Obviously, this method will give several possible answers, but we will see later that they are finally quite few (for those which have been tested, of course).

The idea is therefore to build two portions of cipher based on the following models :

For the distance, we’re looking for two numbers (X and Y) written in several possible forms: X AND Y ; X AND Y INCHES ; INCHES X AND Y ; X AND Y IN ; IN X AND Y ; LENGTH X AND Y ; X AND Y LENGHT

For the angle, we also look for one integer X and one fraction Y (X and Y), written in the form : X Y ; RADIANS X Y ; X Y RADIANS ; X H Y M ; X HOURS Y ; HOURS X Y : ANGLE X Y ; X Y ANGLE.

Other patterns are of course possible, but these seem to be simple for a first approach. The solution consists in joining these two portions of code and to test if they respect the constraints of length (32 characters in total) and repeated letters (C, Delta, O).

Note that the precision of the location hidden in the cipher should be of the order of 1km/0.6mi, because the distance is only known with a precision of 1/16 inches (0.4mi with the scale of the map) and I considered that, if minutes are used to express angles, they are only multiples of 5 (wich implies a precision of 2.5°).

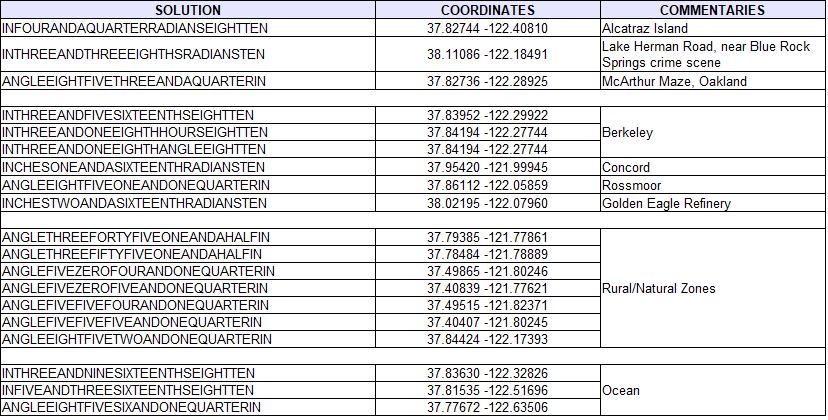
In short, this method leads to testing nearly 4 million possible solutions. Of these 4 million, 65 meet all the constraints (0.0017%). 46 of them lead to locations outside the map and are to be eliminated. Among these 19 solutions, 10 are in the ocean or in completely natural/rural areas. So we have 9 potentially viable solutions that are shown on the map below.

I must confess I have a preference for three of these solutions (in red on the previous map) :

Alcatraz Island, corresponding to the solution "IN FOUR AND A QUARTER RADIANS EIGHT TEN" (4"1/4 8:10)" (note that the exact point of the solution is located at 1.3km/0.8mi from the island, but it’s in the precision range) : this unexpected solution has of course no obvious connection with school buses but I find it interesting : it would simply be a new joke from Zodiak (the bomb was also never found). This is the only solution that respects the separation into two lines of 17 and 15 characters.

A site along Lake Hermann Road, corresponding to the solution "IN THREE AND THREE EIGHTHS RADIANS TEN" (3"3/8 10:00) : this site is located about 1.7km/1.1mi from the Blue Rock Springs scene crime and about 4,0km/2.5mi from the Lake Herman Road scene crime. Here again, there are no obvious references to schools or school buses, but this route is obviously strongly linked to the activity of the Zodiac.

The Mc Arthur Maze in Oakland, corresponding to the solution "ANGLE EIGHT FIVE THREE AND A QUARTER IN" (8:05 3"1/4). An interesting site if the target is indeed road traffic…

Among the six other solutions, five are located in urban areas where it would certainly be easy to find schools nearby given the uncertainties of the measurement : three in Berkeley (three solutions but only two sites, one in Concord, one in Rossmoor). And the last one is located on the site of the Golden Eagle in Avon refinery, East of Martinez.

Below is the full list of the 19 sites: Obviously, it would not be serious to think that this quick review allowed us to find all the possible solutions : but the few solutions that appear with this simplified method already provide some interesting solutions !