As demonstrated before, the z340 exhibits a peculiar characteristic: the 2 most frequent symbols (‘+’ and ‘B’) fall almost exclusively on non-prime positions. Of all 36 instances, only 2 fall on a prime position. This is statistically odd, as measured by Doranchak:
Shuffle experiments show that + will fall only on 0 or 1 prime positions in 3% of shuffles. In 0.7% of shuffles, + and B each fall on 0 or 1 prime positions. So, I can’t easily dismiss the phenomenon as coincidence. More info here: http://www.zodiackillerciphers.com/?p=319
While this primephobia of the most frequent symbols could be a coincidence, it could also be a symptom of the cipher’s construction methodology.
The purpose of this post is to present 2 encryption methods that substantially augment the odds of inducing such primephobia in the resulting ciphers.
Primes in columns
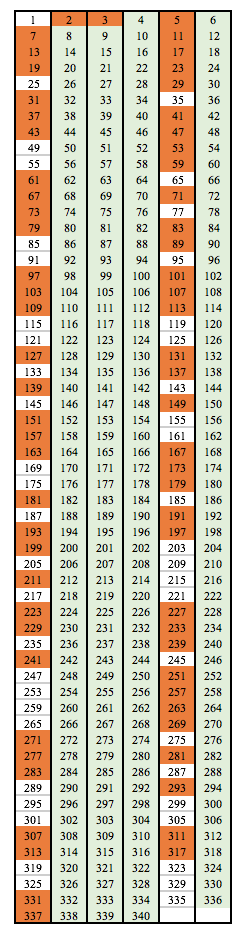
When listing a series of numbers in a table format, an interesting phenomenon can be observed. For example, let’s list all numbers from 1 to 340 in a table of 6 columns. In this table, I have highlighted all the prime numbers in orange:
You’ll notice that, if we exclude the very first line of numbers, all the prime numbers are positioned in columns 1 and 5. Columns 2, 3, 4 and 6, highlighted in green, are prime-safe (again, excluding the first line), meaning that no prime number can be found in these columns. This is because all numbers in columns 2, 4 and 6 are at least divisible by 2 and numbers in column 3 are at least divisible by 3.
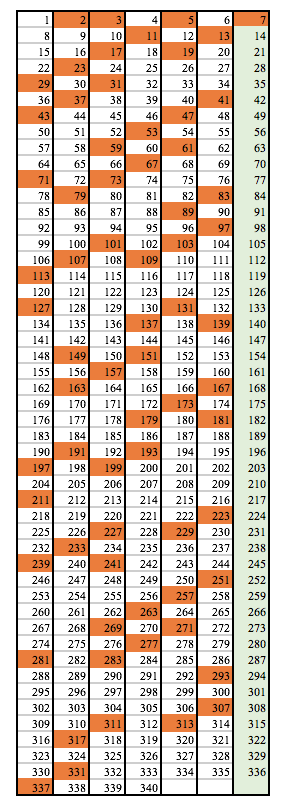
The appearance of these "prime-safe" columns is entirely dependant on the number of columns chosen to display the list of numbers. As a second example, here is the same list of numbers organised in a 7-column table:
You’ll notice that, excluding the first line, only the 7th column is prime-safe, since all the numbers in that column are at least divisible by 7. All other columns potentially can host a prime number.
Here are a few examples of prime-safe columns according to the number of columns used to display the list of numbers :
# Columns Prime-safe Columns --------------------------------------- 5 5 6 2, 3, 4, 6 7 7 8 2, 4, 6, 8 9 3, 6, 9 10 2, 4, 5, 6, 8, 10 ... 17 17 ...
If a cipher construction method were to intrinsically exploit this prime-safe columns phenomenon, it would increase the probabilities of yielding primephobic ciphers. In other words, if the construction method was somehow funneling high-frequency symbols in prime-safe columns, it would greatly increase the yield of primephobic ciphers.
Recipe #1: Vigenère
The Vigenère cipher is a method of encrypting alphabetic text by using a series of different Caesar ciphers based on the letters of a keyword. It is a simple form of polyalphabetic substitution.
[…]
In a Caesar cipher, each letter of the alphabet is shifted along some number of places; for example, in a Caesar cipher of shift 3, A would become D, B would become E, Y would become B and so on. The Vigenère cipher consists of several Caesar ciphers in sequence with different shift values.
[…]
The alphabet used at each point depends on a repeating keyword. – Wikipedia
This repeating keyword makes the Vigenère encoding very cyclical. If the keyword is 5 characters long, it means that there will be 5 different encoding alphabets, repeated over: 1,2,3,4,5,1,2,3,4,5,1,2,etc. Another way to look at this is, for a 5-letter keyword, displaying the plaintext in a grid of 5 columns, every letter of a column will be encoded with the same alphabet. This cyclical quality of Vigenère is therefore very compatible with the prime-safe notion explained above.
For example, given a random english plaintext of 340 characters, we would find on average about 43 letter E and 30 letter T. By formatting this plaintext in a grid of 6 columns, these letters would be randomly spread out across all columns. Now, let’s say we encode this plaintext using Vigenère with the keyword "QDEEZE". When an E in the plaintext is encoded with an E in the keyword, an "I" is obtained. When a T in the plaintext is encoded with a D in the keyword, a "W" is obtained. Since the keyword is 6 characters long, and the keyword letters D and E are in positions 2, 3, 4 and 6 (all prime-safe columns), this encoding process will funnel a high amount of resulting I and W symbols in prime-safe columns.
By generating random english plaintexts of 340 characters and Vigenère encoding them with that "QDEEZE" keyword and only selecting the resulting ciphers where the number of symbols I and W total 36 (to mimic the frequency of + and B in the z340), we get a staggering 54% of ciphers which exhibit a primephobia on these symbols equal or higher than the + and B of the z340. This is in comparison with 0.7% of random shuffles of the z340 exhibiting equal or higher prime phobia than the original z340.
The size of the keyword, its letters and their positions in the keyword will have a dramatic impact on the likelyhood of producing a primephobic cipher.
Recipe #2: progressive key polyalphabetic cipher
This method consists in switching encoding alphabets for each letter of the plaintext. If 5 alphabets are defined, the 1st plaintext letter is encoded using alphabet #1, the 2nd with alphabet #2, etc. The 6th letter is encoded with alphabet #1 and so forth… The number of defined alphabets will dictate how frequently the encoder cycles through these alphabets. This is the same principle as the number of characters in a Vigenère keyword.
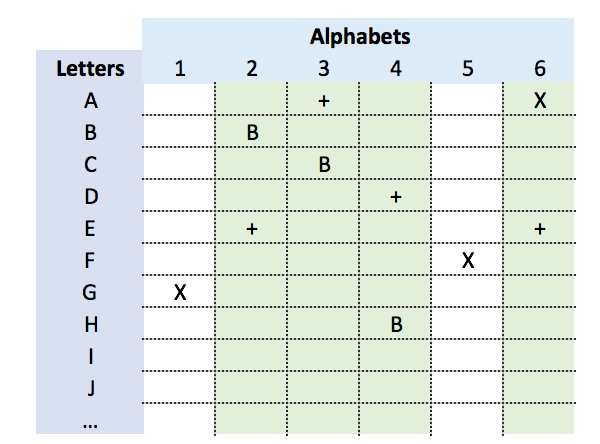
For example, let’s consider this partial encoding table consisting of 6 alphabets where only the +, B and X symbols are mapped:
This means that a + symbol would be decoded to either a E, A or D, depending on where that symbol is found (i.e. which alphabet is used) and a B symbol would correspond to the letters B, C or H. With such an encoding table, the + and B symbols would only fall on columns 2, 3, 4 and 6 (all prime-safe columns), thus yielding a rate close to 100% of ciphers being more primephobic than the z340.
Again, the number of alphabets and how the symbols are assigned to plaintext letters will greatly affect the primephobic cipher yield. But, as with Vigenère, the interesting conclusion is that both these encoding schemes have a demonstrable and significant impact on primephobia by concentrating symbols in prime-safe columns.
I think it is possible that the prime phobia exhibited by the z340 is an indication that a similar cyclical approach (polyalphabetic or otherwise) was used with favorable conditions as to concentrate + and B symbols in prime-safe columns.
_pi
_pi-
That is fantastic work, and absolutely fascinating. I have never thought about nor seen "primes in columns" like that before!
Now what to actually DO with it, I don’t know… But I’m certainly interested in where this goes. 
-glurk
——————————–
I don’t believe in monsters.
I agree that Zodiac could have cycled multiple keys and that could be the explanation for the prime phobia phenomenon. Thank you for showing that with such an easy to understand presentation.
Nice job, pi! This is a very compelling avenue to explore. Thanks for taking the time to put this writeup together. It would be interesting to simulate these possible construction methods more closely, to see how much the results resemble the actual 340.
Interesting and refreshing post _pi.
If a cipher construction method were to intrinsically exploit this prime-safe columns phenomenon, it would increase the probabilities of yielding primephobic ciphers. In other words, if the construction method was somehow funneling high-frequency symbols in prime-safe columns, it would greatly increase the yield of primephobic ciphers.
Can we come up with something like that which is not specifically vigenere and also distributes over a chosen number of characters which behaves like the 340? What we believe to be homophonic substitution in the 340 may be such a process. I have made such an example algorithm like this a while ago but it doesn’t seem to correlate well with the 340: viewtopic.php?f=81&t=2218&p=29105&hilit=mimic#p29105
Also I’m not 100% sure but I remember something about the "+" symbol positions being close to modulo 5 and 10. It was just an observation without a math check.
Here is a cipher which uses vigenere and homophonic substitution encoding with a 5 letter keyword.
1 2 3 4 5 6 7 8 9 5 10 11 12 13 14 15 16 17 10 18 19 8 9 20 21 22 23 24 25 26 13 27 2 28 29 1 30 31 32 24 17 4 7 8 20 33 9 34 23 3 35 36 37 27 14 38 39 40 25 6 11 28 24 38 14 41 42 31 38 22 11 29 43 37 39 44 26 45 46 10 33 11 36 35 26 5 28 1 28 30 12 25 43 15 47 19 41 31 20 25 4 16 48 49 50 12 32 14 2 26 40 24 37 17 6 44 7 21 18 20 3 13 34 17 24 27 16 32 8 35 45 42 41 29 43 21 38 40 17 14 1 5 21 2 46 9 42 37 2 10 42 23 13 15 39 19 30 8 47 11 21 4 28 29 23 1 2 30 10 18 44 34 12 9 45 27 32 33 38 34 35 25 22 36 46 41 47 45 15 35 43 47 40 20 36 19 3 29 49 12 11 28 28 29 30 45 4 9 42 44 1 47 7 10 20 39 25 31 37 15 10 26 3 47 35 4 7 48 49 46 8 9 50 20 36 24 13 40 27 50 28 17 16 18 8 43 5 33 43 21 26 7 14 46 17 41 16 43 35 34 26 38 1 29 11 19 24 7 1 19 41 11 9 37 15 8 36 50 21 10 41 23 1 2 14 40 16 34 49 6 45 7 40 27 42 23 31 50 38 34 22 30 24 25 14 8 27 33 6 14 26 38 27 3 5 41 16 27 34 15 14 50 45 35 49 11 28 32 49 28 44 20 10 24 2 46 30 3 49 12 5G&7J?FD[J;<*'M=Y C;B:D[,3UNQ1+'@GS .5"V2QC7FD,
Forget it ,a 1000 people working for a 1000 years could not crack it and if they did how would they know they have it , with out the code key ……but + is all but one vowel and frequent letters…I think
Thanks doranchak,
I meant 5 or 10. And that some are close, 64, 81, 159, 201, 211, 291. It’s something that I noticed more than a year ago, when I first started working on the 340. I guess it ain’t much but _pi’s 5 column distribution example reminded me of that.
Modulo 5: 20, 40, 64, 65, 72, 81, 105, 128, 133, 140, 142, 159, 162, 172, 201, 211, 237, 238, 255, 276, 282, 290, 291, 340.
Hmm, too many numbers would be included if we marked the "close" matches too.
[1] 2 3 [4] [5] [6] 7 8 [9] [10] [11] 12 13 [14] [15] …etc…
60% of all integers are divisible by 5 or are only 1 away from such a number.
Thanks for the good words and feedback!
Can we come up with something like that which is not specifically vigenere and also distributes over a chosen number of characters which behaves like the 340? What we believe to be homophonic substitution in the 340 may be such a process.
One way I found to channel certain symbols into prime-safe columns, as I described in my original post, without involving a poly-alphabetic approach, is to assign a homophonic symbol to a letter based on its position in the plaintext. This way, you again find the cyclical component required to induce this prime-safe effect.
So, in the context of a purely homophonic substitution cipher, let’s say the letter E can be mapped to the following 6 symbols: !, @, #, $, % and ?. When encoding the letters E in the plaintext, instead of randomly assigning a symbol or following a traditional cycle through all the 6 symbols, you would advance in the cycle at each position in the cipher. At position 1 in the cipher, if an E is present, it would be mapped to !. For position 2, if an E is present, it would be mapped to @. Etc. Following this logic, symbols @, #, $ and ? would be highly prime phobic in the resulting cipher as they lie in prime-safe columns in this homophonic assignment cycle.
This approach was clearly not used in the z408 and probably not in the z340 but, for the sake of this conversation, it would be a homophonic mono-alphabetic encoding methodology yielding a high ratio of prime phobic ciphers.
Pushing this idea further, using such a positional way of assigning homophonic symbols could be a way to avoid confusion in the case where polyphones are involved. Let’s say that the z340 is similar in construction to the z408 but it contains way more polyphones. One way to make the cipher decodable would be to select the polyphone assignment based on its position. For example, the + symbol could be translated to E in position 1, B in position 2, etc.
One way I found to channel certain symbols into prime-safe columns, as I described in my original post, without involving a poly-alphabetic approach, is to assign a homophonic symbol to a letter based on its position in the plaintext. This way, you again find the cyclical component required to induce this prime-safe effect.
Interesting, could you make an example cipher?
Interesting, could you make an example cipher?
cDBPbqcDDBs8u+STh +4+k3yWaBCBxxtQy5 o7ysBCdW2SU+mXsC9 3sqcDDBP8ZBDKM3r+ Bsf9amSUU+xC4+J3y x+rHscxC9brtxClHR n+USXxiPBrHDtL3Dh CtqBDhxtQ+C9BRnnB Y+x2+Co+2SWCfNUBD DdsM+EVbUaP5+dCcW +zbs4+CCbUe93RM+e CBsnFtyUwO5qxSmLA cCo38BUDC9b4axCTH weSmBfBxCo3fZo+sB 6BaBZBhDI+w+ISUsB Ru3w3lBk+is63hDe9 +B93Y+qBhDa6ABhD4 +JS2+rFWDHYaWBZdD gPSCnBY+1SXrFP3Qb jaJ3XW+FSXAdDgCUF fSWDSZlSZRSwxCtu2 1JSgD+JfBsnSmWDiz +xLSUQ137CaVDBL+a j+SUBaC+rbCNoVBfB
I re-encoded the z408’s plaintext using this scheme. The resulting cipher is easily solvable in a few seconds in zkdecrypto.
This homophonic cipher is therefore of length 408. It uses 59 different symbols. The most frequent symbols are B, +, C, D, S and 3; together, they occur 148 times, covering 36% of the cipher. Of all of these 148 occurrences, only 2 are primes, making these symbols 99% prime phobic.
The encoding scheme, in more details, is the following:
For the following letters, choose the symbol whose position in the list cyclically corresponds to the plaintext’s letter’s position in the cipher:
Letter: Symbols --------------- A: i 3 3 3 H 3 E: a + + + b + I: c B B B d B L: g D D D h D O: t S S S O S T: e C C C f C
In other words, if X is the position of the letter in the cipher, pick the symbol at position X % 6.
For all the other plaintext letters, randomly choose a symbol from the list allocated to that letter.
This is obviously an exaggerated example but it demonstrates that, under the right conditions, using such a cyclical way of picking symbols when constructing a homophonic substitution cipher, the resulting cipher could exhibit prime phobia for 1 or more frequent symbols.
_pi
Thanks _pi.
This is obviously an exaggerated example but it demonstrates that, under the right conditions, using such a cyclical way of picking symbols when constructing a homophonic substitution cipher, the resulting cipher could exhibit prime phobia for 1 or more frequent symbols.
Yes, I think your cipher is about 4 times as prime phobic as the 340. There is also a huge odds/even discrepancy which can be noted for the 340 also (though not to this extent). I tested your cipher with my m_s2_cycles measurement for homophone sequences and it scores below average so the cycles are fully randomized.
That’s really interesting because that correlates with the 340 to some degree. I wonder if a similar table was used, where one non-prime column is selected as a polyalphabetic. This could explain some of the randomization and the prime phobia!
Letter: Symbols --------------- A: i 3 3 3 H 3 E: a + + + b + I: c B B B d B L: g D D D h D O: t S S S O S T: e C C C f C
I also wonder if it could relate to this: http://cypherpunks.venona.com/date/1993 … 00354.html Although I don’t understand how to apply the encoding, which is described as second order homophonic substitution.
I made a measurement for this. For each set of symbols sum all the modulo frequencies using c*(c-1) and divide that number by the frequency of the symbol. It seems to work perfectly! It filters out the "prime" suspects in the 340, 408 and pi2 ciphers. Sorted by score, the field on the right is the score.
Stats for: 340.txt ----------------- Symbol number by appearance, ASCII symbol, frequency, score. ----------------- 19 + 24 21.83 20 B 12 12.5 16 2 9 8.88 3 R 8 8 56 C 5 6.4 8 V 6 5.66 51 F 10 5.6 23 O 10 5.4 28 . 6 5.33 22 # 5 5.2 21 ( 7 5.14 50 5 7 5.14 29 < 6 5 39 Z 4 5 6 l 7 4.85 42 S 4 4.5 5 p 11 4 7 ^ 6 4 18 N 5 4 10 k 5 3.6 48 t 4 3.5 36 c 10 3.2 31 K 7 3.14 40 z 9 3.11 4 > 4 3 62 A 2 3 33 ) 5 2.8 12 1 3 2 43 7 3 2 47 9 4 2 49 j 2 2 53 4 6 2 61 b 3 2 55 - 5 1.6 44 8 4 1.5 11 | 10 1.4 14 T 5 1.2 17 d 5 1.2 26 W 6 1 27 Y 4 1 30 * 6 1 32 f 4 1 52 & 2 1 2 E 3 0.66 9 P 3 0.66 46 _ 3 0.66 54 / 3 0.66 58 ; 3 0.66 37 M 7 0.57 25 D 4 0.5 41 J 4 0.5 38 U 5 0.4 15 G 6 0.33 1 H 4 0 13 L 6 0 24 % 2 0 34 y 5 0 35 : 2 0 45 3 2 0 57 q 2 0 59 X 2 0 60 @ 1 0 63 6 3 0 Stats for: 408.txt ----------------- Symbol number by appearance, ASCII symbol, frequency, score. ----------------- 26 q 16 16.37 6 U 10 11 7 B 12 9.83 14 W 9 9.33 2 % 11 8.18 1 9 14 8 36 D 6 8 29 ^ 6 7.66 32 T 7 6 15 V 9 5.55 11 = 7 5.42 3 P 11 5.27 8 k 9 4.88 22 H 8 4.5 50 8 8 4.25 23 @ 6 4 30 I 11 4 33 t 7 4 39 S 6 4 42 A 8 4 45 E 9 4 27 M 8 3.75 4 / 6 3.66 13 X 9 3.55 10 R 12 3.5 21 6 8 3.5 37 5 8 3.5 54 _ 8 3.5 46 L 8 3.25 17 e 10 3 9 O 7 2.85 41 # 10 2.8 49 5 2.8 16 + 8 2.75 47 d 6 2.66 38 ) 8 2.5 5 Z 8 2 44 l 5 2 19 Y 10 1.8 48 r 7 1.71 28 J 6 1.66 12 p 6 1.33 43 f 3 1.33 52 c 6 1.33 24 K 5 1.2 25 ! 5 1.2 20 F 6 1 40 ( 4 1 35 Q 5 0.8 34 N 6 0.66 18 G 7 0.28 31 7 3 0 51 z 4 0 53 j 1 0 Stats for: pi2.txt ----------------- Symbol number by appearance, ASCII symbol, frequency, score. ----------------- 3 B 33 39.03 10 + 33 35.51 2 D 23 30.26 20 C 24 25.91 11 S 20 23.4 16 3 15 16.8 7 s 13 8.15 36 r 7 8 21 x 14 7.85 4 P 6 6.66 29 U 13 6.61 23 Q 4 6 18 W 9 5.55 41 R 5 3.6 32 9 8 3.5 8 8 3 3.33 6 q 5 3.2 51 F 5 2.8 52 w 5 2.8 24 5 3 2.66 30 m 5 2.4 12 T 2 2 59 j 2 2 33 Z 6 1.66 31 X 5 1.6 44 L 4 1.5 13 h 7 1.42 25 o 6 1.33 48 V 3 1.33 54 A 3 1.33 19 a 11 1.27 14 4 5 1.2 27 d 5 1.2 1 c 6 1 5 b 8 1 49 z 2 1 28 2 5 0.8 35 M 3 0.66 58 1 3 0.66 38 J 5 0.4 39 H 5 0.4 42 n 6 0.33 22 t 7 0.28 37 f 7 0.28 9 u 3 0 15 k 2 0 17 y 5 0 26 7 2 0 34 K 1 0 40 l 3 0 43 i 3 0 45 Y 4 0 46 N 2 0 47 E 1 0 50 e 4 0 53 O 1 0 55 6 3 0 56 I 2 0 57 g 3 0
Here’s the measurement function that gives a raw score for the full cipher. Requires the input cipher to be numbered by appearance. I named it m_spmf, stands for symbol position modulo frequencies. What else?
Usage for 340: m_smpf(cipher(),340,63,2,170). The last two arguments determines the from-to modulo range. No more than half of the total_symbols needs to be entered for the mod_to value since only 2 numbers can be modulo 170=0 by this length, 170 and 340.
Output:
340: 181
408: 205
pi2: 268
To compare it to other ciphers it’s probably best to calculate the percentual difference from the randomized average. I think the 340 is fairly normal in this regard but some symbols stick out.
function m_spmf(cipher()as short,byval total_symbols as short,byval unique_symbols as short,byval mod_from as short,byval mod_to as short)as double dim as integer i,j,k,t dim as double score dim as short symbols(unique_symbols,100) for i=1 to total_symbols symbols(cipher(i),0)+=1 symbols(cipher(i),symbols(cipher(i),0))=i next i for i=1 to unique_symbols for j=mod_from to mod_to for k=1 to symbols(i,0) if symbols(i,k)mod j=0 then t+=1 next k score+=t*(t-1)/symbols(i,0) t=0 next j next i return score end function
