Posted by: @richard-grinell

We don’t actually know how the Zodiac calculated the distance in miles …

He didn’t. Map in ‘inches’. Ruler measures ‘inches’. Code in ‘inches’.

Posted by: @richard-grinell

… some technique using code solving rather than cipher solving, probably needs applying.

My own personal approach is, certainly, one based upon a degree of optimism that feel I can be justified in taking as the biggest gain of all from the recent success, in 2020, of seeing the 340 finally solved. Clearly, the first two ciphers were, despite the presence of somewhat distracting ‘errors’, of sufficient coherence that they could finally be cracked. From their content, particularly in the case of the Z340, it is further evident that it has always been the expectation of the Zodiac that success would be reached, in both cases, if only with effort. In my optimism, then, I am looking to begin with the assumption that the same is the case with the Z32 — that, despite how it superficially appears, we have in all likelihood been given enough to derive the intended solution in some way that can be demonstrated to be correct.

Of course I have to acknowledge, with everyone else, that the meagre constraints posed by a 32 character cipher comprising 29 unique symbols give nothing of any real help of themselves. This is why, in my optimistic mindset, I am testing out the view that this is, in fact, not actually the limit of the constraints upon the 32 at all.

Certainly, it would not be helpful just to randomly start introducing arbitrary additional constraints with no rhyme or reason. So, we look elsewhere and notice — I’m sure not for the first time — that there are patterns of cipher symbols, or n-grams that, to some degree or another (certainly as to order), repeat in both the Z32 and the Z13 in a manner that I, for one, am keen to test as to their being intentional — that the keys for these two ciphers, at the very least, are not independent.

The question for me, then, becomes whether it is possible to clarify just what the specific scope and nature of their apparent inter-dependency might be, and for this I introduced a set of assumptions proposing not only a common key for both, but actual common words across both ciphers. The result of doing so — as was expected, and as was my intention — is that this went on to add significantly to the constraints now imposed on the Z32, such that the likelihood of any attempt at solution to the same producing a random incorrect result would be likewise reduced in some degree. As it turned out this applied set of constraints, arising just from the initial assumptions, was such as to all-but dictate how the solution fell out. Then, once obtained, the resultant key was open to be analysed for further indication of intention, through the search for features therein that would be considered to rise significantly above random occurrence.

It’s this evaluation stage that I’m currently at, and would still invite others to help with. That said, I do strongly feel that the above provides the general method that ought to be pursued in search of a definitive (!) solution to the Z32.

We cannot, of course, demand that the Zodiac was successful in giving us something of this nature to direct us to a unique solution, but I’m more than ever convinced that he did, and that he will have given it a good try.

Posted by: @shaqmeister

Of course I have to acknowledge, with everyone else, that the meagre constraints posed by a 32 character cipher comprising 29 unique symbols give nothing of any real help of themselves. This is why, in my optimistic mindset, I am testing out the view that this is, in fact, not actually the limit of the constraints upon the 32 at all.

Ok, so I’m not exactly sure what it is I might be hoping for here, but I’m wondering whether we can get any help towards evaluating the scope of the field of potential solves from, first, applying the extended constraints from the assumptions in my first post to the Z32 and then letting AZdecrypto take a look at it. At this point I can only admit that I have little to no acquaintance with the functionality that this software offers that might be useful in this instance, although its evident power in tackling ciphers of reasonable length, such as the Z340, is proven.

Just to be clear, though, with the extended constraints being even now only such as are summarised in the following graphic, as so …

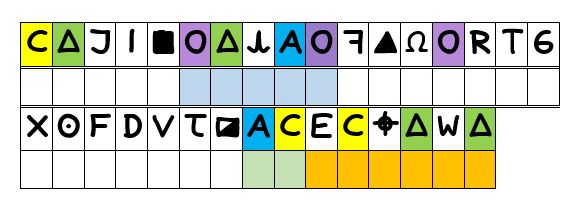
… it has to be acknowledged at the outset that feeding the text equivalent of the above into any such software — that is:

C9J|#O9[AOf8?ORTG
X6FDVj%ACECz9W9

would not, of itself, be sufficient to capture all of the required internal constraints, which have to likewise include those imposed by the limits of the three identified word blocks. Recall, it was in the nature of the assumptions that the very occurrence of the extended plaintext repeats arose out of first delimiting the words blocks such that, subsequently, these two constraint forms cannot be separated out.

Equally, alongside the internal constraints as can be readily laid out in precise fashion, as above, the situation with the Z32 is that there is a necessarily present, but unfortunately vaguer, body of external constraints to be taken into consideration. We know the plaintext helps us to pin down a specific location with the aid of the map. There are, therefore, words that we would like to give priority to in limiting viable solves — numbers as words, such as ‘ONE’, ‘TWO’, … ‘NINE’; units for both a bearing and a range; ‘INCHES’ is almost certainly going to be in there somewhere; possibly some or other conjunctive, such as ‘AND’. Again, it would be necessary to investigate first whether advanced decryption software such as AZdecrypto includes the functionality to set prioritised crib lists and such.

That, and start to familiarise myself with the internals of how such software operates generally, which might take some time!

Posted by: @shaqmeister

That, and start to familiarise myself with the internals of how such software operates generally, which might take some time!

But, before launching out on such a challenging venture, maybe it’s worthwhile to first run a little math. Specifically, let’s first make an attempt at calculating that magic number — the ‘unicity distance’ — as it relates to the Z32 as given, and as assumed to comprise a simple homophonic substitution cipher. Deavours (below) explains why this is a measure worth applying in the context of the current evaluation.

Deavours (1977), p. 46

“The unicity point of a cipher is the message length beyond which decipherment using a known system becomes a unique process. For messages shorter than the unicity point distance, plural decipherments are the rule and the would-be cryptanalyst has no possible method of selecting the correct decipherment from the many available ones.”

The formula that Deavours offers for calculating the unicity distance, U, is (loc. cit.):

U = H(k)/D

Alongside U, and in the manner in which I will make use of this formula here as applying to the solution of a simple homophonic cipher, the remaining terms can be given as:

• k: the size of the theoretical key space (with formulae to come, below);
• H: function giving the resultant ‘entropy’ of the key space, k, corresponding to log₂(k); and
• D: the ‘redundancy’ of the English language in bits per character, with a current generally accepted value of 3.2.

As for determining the size of the theoretical key space, k, Dhavare et al. (2013, p. 253) give the following equation:

k = ⁿC₂₆ × 26! × 26^{n − 26}

where n is the number of unique symbols in the cipher key.

Plugging in the appropriate numbers, for the Z32 (n = 29) we get a calculated unicity distance of 36.

Needless to say, therefore, with a cipher length of just 32 characters, by the above method the Z32 is deemed to be too short, of itself, for its “decipherment using a known system [to become] a unique process.”

Of course — and stepping aside for a moment from the Z32 — were we to reduce n down from 29 to 26, equal to the length of the plaintext alphabet, we would reach the unicity for a simple substitution cipher without homophones. The equation for k would reduce to just its middle term on the right-hand side — i.e., we would have k = 26!. In turn, U would then become 28 (rounded).

There is, however, no meaning to reducing n below 26 for the plaintext alphabet size, and the equation for k correspondingly fails at the attempt on the first term. Thus, we cannot claim that we have improved the unicity distance for the Z32 through having reduced the number of unique symbols to 24 through the introduction of the tighter constraints, as above.

That said, there might be some superficial meaning to calculating the unicity distance for a cipher set of 24 unique symbols against a partial plaintext alphabet of, say, 15 letters, this being the size of the partial alphabet corresponding to the same set of common symbols as they occur in the Z340. This would then allow us to propose a refined unicity distance of 30, which might just seem enough. However, in reducing the alphabet in this way we have merely introduced the further unknown of not being able to specify just which these 15/26 letters are and have thus, in fact, gained nothing.

It certainly looks, therefore, like the efficient and agile hill-climbing of AZDecrypto is not going to be of any help here after all.

---

References

• Deavours, C. A. (1977). “Unicity Points in Cryptanalysis.” Cryptologia. 1(1): 46–68
• Dhavare, A., Low, R. M. & Stamp, M. (2013). “Efficient Cryptanalysis of Homophonic Substitution Ciphers.” Cryptologia. 37(3): 250–281

Posted by: @shaqmeister

It certainly looks, therefore, like the efficient and agile hill-climbing of AZDecrypto is not going to be of any help here after all.

As it happens, there is little to worry about here in any case, and a separate manual attack has been found to be sufficient in the investigation of the widest possible set of potential candidate sets for the Z32. This has been added elsewhere to the thread ‘Approaching the two remaining ciphers as chess ‘problems’’ so that, here, we can be freed up for other things.

Given that the outcome of the work offered in this thread has been to result in what is effectively a co-solution to both the Z32 and the Z13, it would seem appropriate to expend a little effort seeing if it may be possible to reconstruct how the Zodiac may have progressed, in composition, from the one to the other. This could only be a speculative pursuit, even were we to be certain that the solution given is the correct one. Nonetheless, we shall give it a go and commence with the possibility that the Z13 actually started out as a nothing other than a condensed variant of what was later the Z32.

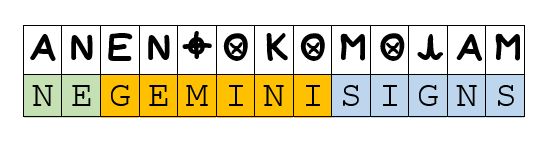
As in the noted analysis elsewhere of the Z32 (see link, above) it would be reasonable to propose that in the case of the Z13 also the plaintext was originally composed in ordered and coherent fashion. For this reason, therefore, it will be speculated that the cipher originally began its life as below:

The implication here is that, once solved (if at all possible, on its own), we would be in some way expected to notice the number in the thrice-repeated ‘8-ball’ and understand the whole as conveying “eight signs NE Gemini.” In line with the interpretation given for the solution from the Z32, what is yet lacking here is any specification of either where the envisaged starting point of the bearing is to be (Mount Diablo), or to what range we are to look from it once found.

Two things, of course, assist in regarding the information given in this manner as not wholly deficient. The first is merely the presence of Mount Diablo in close proximity to the Bay Area, coupled with a historical context for regarding this as the focal point of the geological surveying of large swathes of the eastern seaboard, including California. Second, it should only really have been the expectation of law enforcement at the time that the Zodiac had moved his hunting ground and overall focus into the City of San Francisco in any case, so a mere bearing pointing in that direction can have been expected to have given enough of a prompt. Whether this is, or was, a misguided position to take doesn’t need to be considered further for our purpose here.

So, having the cipher and its plaintext as suggested above, what might the Zodiac have wanted to do next? Send it as it is? Possibly, but then its not difficult to notice, even without the benefit of hindsight, that there is a lot of potential in the repeating cipher symbols for mixing things up, just a little, to gain a gratifying, multi-layered symmetry. I propose that this symmetry was, then, something that the Zodiac would have strived for at this point.

He doesn’t want to mess things up too much, of course, so the first step is to merely get the three ‘8-balls’ nicely spaced, and this is easily achieved without breaking up words, as here, through simply shifting over ‘SIGNS’ from the beginning to the end.

Only now, it is far too distracting not to picture the three ‘8-balls’ nicely aligned about the very centre of the cipher, and so this is permitted to be achieved, even at the expense of having to break up the first two characters, and we thereby end up with the familiar Z13 as we know it.

Note that the choice of shifting the second cipher symbol, ‘N’, all the way up to the third from the end not only brings about the sought-after centralisation, but further adds itself into a symmetry relation with the now third symbol in the final cipher.

So now, having noted that not only has no-one succeeded yet in deciphering this first attempt at giving his bomb location, but even the previous longer cipher sits untouched, awaiting a further half a century to reach solution, the Zodiac, therefore, seeks to try again with the bomb code and this time, at the very least, sends a map too to pin down the starting point on Mount Diablo.

Symmetry is not going to be a concern in relation to his new, longer, cipher so, instead of the Z13 as we have it, the Zodiac sets out from the contextually-ordered version given above as likely the former’s first incarnation. Having feared that the value for the bearing specifically was missed in the ‘8-balls’, he wants to add this in at the start explicitly as ‘EIGHT’. Likewise, his feeling is that he probably ought to give the range also and so, with the implicit help of the scale on the map, he looks to interpolate ‘PLUSFOURINCHES’. So now, having reached the encoding stage, he is beginning again with:

So, how to proceed from here?

Well, as discussed in detail elsewhere in the linked thread (see above), we shall continue under the assumption that the Zodiac’s intent — whether actually met, or not — was always for the cipher to be decoded and the bomb location retrieved. For this reason, then, he is expected to have intentionally introduced the helpers we have identified.

Firstly, then, he manifests the clear link between the Z13 and his new cipher through directly carrying over the relevant symbol from the former in a number of selected places, as below (red).

It is the Zodiac’s hope, and expectation, that we should easily spot these parallels.

Next, he wants also to carry over the fact that the three ‘8-balls’ are all ‘I’s, but he does not wish this to be too obvious. So, instead of merely copying these over to the new cipher also, he does something different instead to the same effect — he replaces each in turn, uniquely, with one of the four symbols that had encoded ‘I’ in his first cipher, the 408, and hopes that we shall pick up on this also.

As the penultimate step, then, the Zodiac introduces a sparse few symbols that will form the only repeats in the cipher text that will be present in the end result.

The choice of where to set the duplicates appears not to be random either. There is a clear and apparent tendency to mark the beginning and end of words or, at the very least, blocks of words. Further, the duplication of the symbol encoding the final ‘I’ at position 2 effectively pins down the bearing, whilst the duplicate ‘C’ from the first letter of the cipher does the same to get the second letter of ‘NE’.

All that is left to do, at this point, is to randomly fill in the remaining encodings with unused symbols and copy the ciphertext into a letter for posting along with the Phillips map.