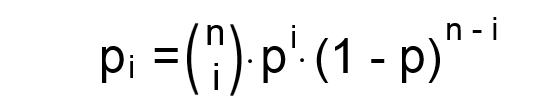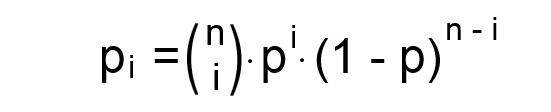Ok…for the first time ever I can see an approach of how the 340 might be cracked..

Facing 63 symbols, all possibly representing 26 alphabetical letters leads us to the broad range of 63^26 or 60.65 x 1,000,000,000^5 theoretical combinations of how the letters can be placed. Tough task.

Luckily we got some linguistic issues, such as vowels or consonants in such a cleartext. Plus some statistical values for letters, bigrams and trigrams etc. from other texts.

Now an approach is to combine some of those methods together. If this doesn’t help, even with guessing the cipher probably will never be solved.

However we can make some assumptions to get closer to a solution (for a homophone cipher):

1. Double letters are frequent ones, therefore not QQ, XX etc. but e.g. LL, EE, TT,…we therefore are able to focus on the e.g. the eight most frequent double letters. The 340 has two different double letters, ‘pp’ and ‘++’ and can those be combined to each other, resulting in e.g. 8×8=64 different varieties. In fact, we can rank those combinations according to their double letter frequencies.

2. We also got two reverse trigrams, ‘pO+’ and ‘+Op’. Therefore we can take some dozens of frequent reverse trigrams (cleartext) such as FIL and LIF which could represent the words FILL and LIFE. Those we can combine with our varieties of double letters, leading to e.g. 64 x 120 = 7.680 different varieties.

3. Then we got two repeating trigrams, those luckily being combined to a five letter combination, the ‘IoFBc’ symbols. Some frequent trigrams combined with a some other frequent trigram will give us a variety of approximately 400 different combinations (e.g. ‘THERE’), therefore 400 x 7.680 = 3.072.000 different varieties. This is an amount which is at least ‘computable’. Those 400, however, can be ranked according to their frequency, the correct combination might therefore be amongst the first few 7.680’s, e.g. 76.800 varieties.

4. Finally we go for a frequent bigram, e.g. ‘SP’, and will we get a 10-letter text phrase out of which 3 letters are still unidentified. This however could be completed by a.) guessing or b.) by comparison to the 9-letter text phrase which includes the ‘IoFBc’ trigram combination.

Besides the fact that – given the framework above – we have identified 32% of the cipher, the two text phrases of length=9 and length=10 should be enough to find some partial linguistic solution. The problem, of course, is the remaining amount of varieties (had stopped with the Dorabella cipher for that reason, with approximately 250,000 varieties left over and no clue left over to proceed..).

So far, except computer solving methods or simple guessing, I can’t see any closer approach to crack it..

Please note that the reverse trigram infact defines the two double letters, although we still might not know which one is representing the ‘p’ and which one defines the ‘+’ (because it’s a reverse one..). However we may select the reverse trigram according to the double letter frequencies of its first & last letter.

QT

thanks for the thorough and well presented work. you said "or simple guessing" but i’d like to make the point that there is nothing wrong with guessing as long as it’s consistent and the less we have to guess (by using methods such as yours to place as many characters as possible) the easier it is to guess correctly.

the problem with every "solution" ive seen is that they’re almost completely random. a character is "e" here and "g" there, or the "solution" is found by randomly choosing decoded letters to spell things out. the real solution will be similar to the 408 in that it will follow a simple set of rules consistently (except for maybe a mistake or two, since we know he made a lot of mistakes).

the rub to the 340 is that he took another step, one not present in the 408, and we don’t know what that step is. we do know that solving by using previous words of his hasn’t helped at all, dictionary attacks haven’t worked, the hill climbing approach can’t find anything, etc. to me this indicates one of two things – 1) it’s not a substitution cipher, or 2) it’s a substitution cipher with a trick such as no "e" usage, or he intentionally used a carefully crafted set of words (say a pool of 150 words), or the cipher isn’t read left to right. my concern with #1 is minimal. if someone figures out what he was doing it’ll be obvious when the cipher is solved. #2 worries me more because if he simply did a substitution with scrambled letters then we’ll never in a million years get a consensus on what he was saying. he wasn’t a gifted encoder so scrambling letters makes sense as an easy way to make the cipher harder, however we’ve seen in this forum and others that you can give ten people twenty letters and they’ll come up with fifty things the letters unscramble to say.

as always, just my 2 cents.

…i’d like to make the point that there is nothing wrong with guessing…

…the rub to the 340 is that he took another step, one not present in the 408, and we don’t know what that step is…

…he wasn’t a gifted encoder so scrambling letters makes sense as an easy way to make the cipher harder…

…and they’ll come up with fifty things the letters unscramble to say…

as always, just my 2 cents.

Absolutely, guessing is a good approach, however so far it didn’t work due to the huge amount of possibilities.

He made the 340 harder by using a shorter cleartext combined with more homophones than in the 408, we do know that sort of. Nevertheless it could be solved by e.g. ZDK..this still doesn’t work, many reasons for that: E.g. certain vowel/consonant constellations, rare double letters, using of names, settings of the solving options etc.

The good thing is that it’d be hard if not impossible to find a second (different) solution if one is found..this however would still not work because a solution will give some content, the message, so finding a linguistic correct solution would not necessarily deliver some text message to be understood by the reader. So if a valid solution can be found which has some sense in it, we can be sure that it is finally the correct one.

QT

Quicktrader et al., I’m sorry to be so dense but do admire your work even though I cannot begin to understand it as I’d have to take an entire bottle of Excedrin to rid myself of the cipher headaches I get when I try!
With that being said, those double letters got me thinking. The ++’s of course remind me of Z and the TT’s made me think of words like "betting", "netting", "getting."

FWIW, it made me recall a conversation I had with my guy while sitting on the beach many years ago when we were talking about any and everything under the sun. One of them was computer programming as I’ve mentioned elsewhere. He proceeded to write his name in code for me in the sand and I had to guess what it was. After several tries, I gave up and once he explained it, I couldn’t see how I’d failed to get it the first time.

We then went on, talking about time and LEAP YEAR which it was that year or was going to be the coming year. (We met in 1970 so it was then or the following year that this convo took place IIRC.) I’m almost positive then that he made some pretty coy remarks about "leapfrog" in his playful manner and I asked him if he’d ever played that as a kid and he made some rather mysterious remark about it.

Sorry to be so long but just trying to give you an idea about where my idea is coming from. I tried googling to see if there was a leapfrog code but get all the current stuff that wasn’t around back in the 1970’s. I then googled leap frog ciphers and think there are some but I can’t understand enough to even guess if that was used to write the codes. I did see something about double letters and "TT" so am just commenting here for you as a possible clue in case this is a real way to write codes and ciphers and hasn’t already been considered.

the problem with the double letters is not knowing if they’re in the same word or the end/beginning of two words. in either case, combos like "xx" or "zz" are unlikely, but others are more likely as parts of two words.

the problem with the double letters is not knowing if they’re in the same word or the end/beginning of two words. in either case, combos like "xx" or "zz" are unlikely, but others are more likely as parts of two words.

True..the first ‘++’, for example would determine the previous symbol ‘o’ to be either the opposite of ‘+’ being a vowel/consonant or could both be consonants if there is a word gap inbetween, e.g. ..STTE..

QT

Sloooowly we are getting closer.

We do know some statistical data out of millions of letters used in various books. And we do know that a bigram consists of 26×26, therefore 1 out of 676 possibilities. Out of those, however, only 44 are expected to appear more often than twice, e.g. 2.09 times in a 340 cipher. Let’s assume that those 44 consequently are ‘interesting’, however we’ll only check out the 20 most frequent ones.

Then we’ve got a list of some 180 (frequent) trigrams, with few of those being readable in both directions. We had previously called those ‘RevTrigs’. Let’s assume them to be a group of 68 of such revtrigs. Some of those might not match the (individual) overall letter frequency of e.g. the ‘+’ symbol, therefore the group is reduced to 41 different revtrigs.

And we got our combination of two trigrams (‘IOFBc’). Those trigrams are expected to appear at least once (if not twice) as they show up twice in the 340. Not all of them can be combined together, therefore we received a list of 403 ‘pentgrams’, most of them to be expected to appear less than 1% in a 340 cipher. But let’s take all of them, in many cases their fourth letter (‘B’) is the same. And rather not an unfrequent one such as Q. So we may get a list of 17, not 26, alphabetical letters that could be placed for the symbol ‘B’. If we only focus on the pentgrams having a chance of 1% to appear in the 340, we even get a list of only 9 letters represented by the ‘B’ (ACEHLNRSV). Then again,

And finally we can start guessing: Let’s simply start and guess two symbols, multiplying all considered above with 676 variations (26×26 again). However those two symbols I got in my mind both appear at least 5 times in the 340, so approximately 6 alphabetical letters might be ruled out, leading to 20×20=400 variations. So far we have not yet considered any of them to be vowels or not.

We get an amount of approximately 20x41x9x20x20=2,952,000 variations. What now? We could and can sort them somehow out, regarding e.g. one of the letters of the bigram and/or one of the guessed ones to be a vowel. That is speculation, but ok.

The point is, it might reduce the varieties to approximately 300,000-400,000, which could be overviewed in a view hours if a linguistic result/word might show up. The list to be checked could then look like this:

Although still long, this would cover the most frequent combinations of two areas of the 340. One starting with the 15th letter in line one, the second starting with the 62nd letter in line four of the cipher. As we can see, it’s quite easy (~) to check out if such two letter combinations might match to English language. The good part of it, the variations are ranked according to their probability to show up in the 340. Just an idea, so far.

QT

Long time no news here around..had to fight with a broken laptop, last file sadly completely gone. But now there is some news.

Some of us may have thought about the chances that three double symbols occur in a 340 cipher. Me too. And it is not enough to simply go for some probabilities of how often a double letter would actually occur in a normal text.

Because his statistical observation fades away with the usage of homophones. Therefore we got to review this issue under consideration of the amount of homophones Z might have used. Compared to the 408, by using 63 homophones, Z has in average increased the amount of homophones per alphabetical letter in the 340. We do assume, however, that he had used a similar (or identical) amount of homophones, nevertheless has increased the homophones in low-frequency letters. I do so because otherwise the statistical significance (later to be focussed on) would even grow higher.

Three main criteria are essential in the following consideration:

The amount of letters expected (overall frequency)
The amount of homophones
The statistical expectation regarding double letters.

Latter I have received from this list ( http://www.wordfrequency.info/free.asp?s=y ) which appears to be more precise (450m words). Indeed, it also covers the main 5,000 words, many of them might have been used by Z.

Let’s jump quickly into a preliminary example:

1. The letter Q, for example, is not frequent (overall frequency) nor frequent as a double letter (double letter frequency). Our double symbol which shows up three times is the ‘++’. Generally, ‘+’ alone has a frequency of 24, therefore Q can be ruled out for two (later even three) reasons:
a.) Q is not frequent enough as it should show up approximately 0.37 times only
b.) Q as a double letter (QQ) doesn’t occur in 5,000 words even once.
It therefore is most unlikely that ‘++’ is representing ‘QQ’.

2. The letter ‘E’, instead, is very frequent (overall frequency) and somehow frequent as a double letter (33 times in 5,000 words). It therefore could – on first view – represent the ‘+’ symbol.

However I will now demonstrate why this is not possible at all.

Please would you allow me a short introduction?
The main reason is that the statistical expectation of three double letters showing up, in homophone ciphers, is in advance being influenced by the amount of homophones. Assume that ‘EE’ would show up, let’s say, 200 times in 5,000 words. With an average length of 5 letters per word (assumed), we could now think about the 340 cipher consisting out of approximately 68 words.

This leads us to

200 / 5000 x 68

therefore an expectation of 2.72 times the ‘EE’ is present in the 340 (this amount is incorrect, in fact it’s much lower). Nevertheless, in fact it could be represented by the three (and this is crucial!) ‘++’ symbols.

BUT:
The letter ‘E’ is represented not only by one symbol. It is rather estimated that ‘E’ is represented by at least 5 or up to 8 different symbols! Even if ‘EE’ would show up three times in the 340, it is most unlikely that those three double letters – accidentially – are represented by always (3×2 times) the same out of those 5 to 8 different homophones! The very reverse, chances are even much greater that other homophones come into play to represent at least one or more symbols in those three expected double letters. Therefore even only one or two different double symbol would show show up in the cipher. This difference is significant as we do not only discuss the double symbols being present twice or three times in the cipher, no…instead we do understand that, assuming ‘E’ being represented by e.g. 8 symbols, the chances for ‘EE’ to be represented three times all by the same symbols is actually very low! It even is low for just the first double symbol!

Shortly described…the MORE homophones a letter is represented by, the LESS is the chance that a double letter (such as ‘EE’) would show up us a double symbol (‘++’) in the 340, too. Even less likely, that the following double symbols are existing of the same symbols.

So what to do? In fact, we do already talk about combinatory mathematics. Everybody of us does know the chance to throw a dice to a 6, which is, throwing once, 1/6. This is easy. But what we’ve got here is way more complicated:

Scenario 1:
Imagine 16 balls in a bowl…with 8 different colors (two each – representing the double letter – and the 8 colors representing some 8 different homophones). We are now allowed to draw 3 times (representing e.g. the expected 2.72 double letters (‘EE’)). Now guess how low is the chance that you draw three times after another ALWAYS the SAME COLOR for BOTH BALLS. In this scenario, not even one ball would be allowed to have a different color. This most likely won’t work, even if you may want to try it at home with your kids.

Scenario 2:
Imagine 2 balls in a bowl only, both of the same color. This would be the case if only one homophone existed for the letter, therefore ‘+’ representing a letter such as Z. Then we definitely get the double homophones all being the same, without any problems. But what is the issue now? First, the letter Z usually doesn’t occur 24 times in a 340 cipher. Second, with only 9 times in 5,000 words it is a bad candidate for showing up three times as a ZZ in a 340. Although ‘everything is possible’, this scenario is even less realistic than our first one.

Scenario 3:
The favorite…what if the amount of homophones (colors of the balls in a bowl) is quite limited, e.g. to three different homophones, AND the expectation of the letter to occur as a double letter is quite high, e.g. 7 times? And in addition to that, let this letter be even a medium to frequent one, too?

All those scenarios above can be calculated.

We therefore are able to say which letter (based on a certain number of assumed homophones and certain assumed double letter frequencies) is the most likely to be represented by three double ‘++’. In the beginning I thought this would be easy to calculate, but I soon realized that it is actually not. Mainly because we got two criteria of ‘balls’ to be drawn, the first double letter symbol and the second one (thus drawing two balls at the same time with the goal for them having the same color). This is circumstantial as we can write down all those combinations even manually down on a piece of paper in form of a probability tree. To make that easier, however, there is the great Bernoulli method to evaluate those chances considered above. Those, however, are still depending on the amount of homophones.

An example:
Let’s assume two homophones for one letter, the symbols A and B. Therefore a double letter can be represented by AA, AB, BA or BB. The chance to get an AA is 0.25 or 25%, same with BB and the others. To get a 3 times in a row ‘AA’ situation is therefore 0.25^3 or 1.5625%. This might be doubled as we are completely satisfied with three BB’s, too (however we don’t expect BAs and ABs hanging around..maybe additionally but that again is against our double letter frequency expectation).

Probabilities for getting an ‘AA’ situation are:

1 homophone: 100% – AA
2 homophones: 25% – AA, AB, BA, BB
3 homophones: 11.11% (1/9) – AA, AB, AC, BA, BB, BC, CA, CB, CC
4 homophones: 6.25% (1/16) – AA, …, DD
..
7 homophones: 2.04% (1/49) – AA, …, …, GG
(every homophone may be combined with every other homophone, therefore e.g. 7×7 in the latter example)

If we now have look at the ‘E’, with – let’s now say 7 – homophones, this is getting different: 1/7 = 0.14285^3 = 0.00291545 or approximately 0.3%. This is simplified, as we only deal with three draws to get those identical double letters in a row.

But what if out of 7 draws, no matter when, 3 identical pairs of homophones show up? What are the odds then?

Great Bernoulli developed a formula for shortening up this tree of probabilities. It can be tested on both, a low and a high numbered basis, and does go like this (German link: http://www.mathe-online.at/lernpfade/Ko … ?kapitel=4):

With

n=number of ‘tries’ (expected double letters of a specific alphabetical letter in a 340 cipher text)
i=number of ‘successes’ (the required three double symbols present in the 340 cipher text)
p=probability of success (the odds of e.g. getting an ‘AA’ instead of an ‘AB’ or ‘AC’,..)

Putting it into the formula, we simply get the probability of how likely it is to get three double symbols at all. This we can do for each alphabetical letter seperately. Beware: We now do assume a certain amount of homophones for each letter, too, so the chances (‘p’) is differing for each individual letter of the alphabet, fully depending on how many homophones are expected to be represented by.

I did make a tableau consisting of ‘overall letter frequency’ & ‘amount’, ‘double letter frequency’ & ‘amount’ and went into the possibilities of getting an ‘AA’ situation which shall depend on 2, 3, 4 etc. homophones. In my excel sheet the formula for each alphabetical letter looked somehow like this:

=FACULTY(G3)/FACULTY(3)*IF(H3=3;P$3^3;IF(H3=4;R$3^3;IF(H3=2;N$3^3;IF(H3=1;L$3;IF(H3=7;T$3;fehler)))))*((1-IF(H3=3;P$3;IF(H3=4;R$3;IF(H3=2;N$3;IF(H3=1;L$3;IF(H3=7;T$3;fehler))))))^(G3-3))

which should be no more and no less than the Bernoulli formula (the ‘if’ refers to the different amount of homophones expected).

I have to admit that I was suprised:

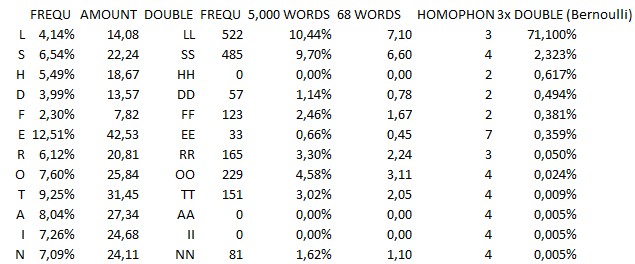
1. Three letters showed up with an ‘error’ as I had not yet defined the precondition of ‘0’ homophones, e.g. Z, Q, J. Didn’t take much care about those.
2. All letters with only one homophone expected showed up with a different error (because the square in Bernoullis formula gets into zero or negative), those were the letters PCMGBZUJKQVWXY. All those letters have an overall expected frequency of 0.09% to 3.06%, therefore would most of them not even be considered to show up more than 10 times (as double and single letterS) – please reconsider: The ‘+’ is present 24 times. Therefore those letters didn’t even reach 46% of what ‘+’ is coming up with. Also none of those letters is expected to show up even twice (therefore not even three times) as a double letter.
3. The letters LSHDFEROTAIN, however, went into a closer Bernoulli-consideration: Those letters gave values on what the chances are that they would show up in the cipher with three identical double symbols.

And guess what:

This is the result. Both, depending on a certain amount of homophones as well as oncertain double letter expectations (latter one based on 450m words). It is the statistical expectation for a letter to appear three times as a double symbol in a 340 cipher.

EVEN IF we assume e.g. the letter ‘O’ to show up with four different types of its homophones (therefore satisfied not only with AA but also BB, CC, DD), the probability doesn’t even increase above the benchmark of 0.1 percent (0.024% x 4 = 0.096%).

Why is that? Why is this so low?

Well that’s explained quicker than what I had written above:
‘O’ is expected to show up only 3.11 times as a double letter (‘OO’). And, due to it’s overall letter frequency, it is expected to have 4 homophones. To draw three times two identical balls at the same time out of a bowl with 8 balls (with putting them back), all of those being colored colored the same, is simply extremely hard.

With 71% it is obviously way easier to draw 7 times, with three colors in the bowl only, to get three times a pair of two identical colored balls (or symbols). It is, imo, not possible to follow that thought ‘immediately’ as such a drawing of balls could look like this (or completely different..many ways, seven levels):

AC, BB, BC, CA, BA, CB, BB, AA, BC, AC, BB

As you can see, in this example it took us 11 draws to complete the three double homophones.

And this is exactly what the table above had told us:
It is not enough to draw 7.1 times and expect three double ‘LL’ symbols. Instead even 10-11 draws are expected to be needed to get those three identical symbol double patterns in the ciphertext.

Accidentially, in the 340, 7.1 draws (occurrances) were enough. Or had Z used the double letter ‘LL’ not only 7.1 times but 10 or more times in his cipher?

What is a fact, however, is that due to a higher amounts of homophones (caused by a higher overall frequency of the letter) and due to lower expected amounts of double letters (e.g. the ‘DD’, which is rather seldom compared to ‘LL’), the other letters do not (significantly!) come into consideration to be represented by the three double ‘++’ symbols.

The first solved symbol, therefore, imo based on valid, significant statistical data, is therefore the ‘+’ representing the consonant ‘L’ (and only that one, as long as no error or absolutely extreme outliers exist).

It should be mentioned, however, that assuming different amounts of homophones (higher ones) would even reduce this probability (lower ones would increase, however the 340 has more, not less homophones). ‘LL’ to occur three times in the 340 is not even expected at all. This would actually requre a value of 100%. Instead it’s 71%. With Z using ‘LL’ a bit more often or the symbols accidentially falling into a good pattern, the triple (definitely exist more in the cleartext) ‘LL’ represented by the triple ‘++’ is, as far as I can say, the only correct solution.

QT

QT-

That’s a good analysis. I haven’t checked your math – WAY too much work for me right now – but I’m sure you are probably correct. The problem, as I see it, and I’ve mentioned this before, is that the 340 is probably NOT just a normal homophonic substitution cipher like the 408 was. So I’m not sure that all of this really helps… That said, I do enjoy reading your posts and I’m glad that people are still working on the 340. I’m a bit lost on what to do with it at this point, to be honest.

-glurk

QT-

That’s a good analysis. I haven’t checked your math – WAY too much work for me right now – but I’m sure you are probably correct. The problem, as I see it, and I’ve mentioned this before, is that the 340 is probably NOT just a normal homophonic substitution cipher like the 408 was. So I’m not sure that all of this really helps… That said, I do enjoy reading your posts and I’m glad that people are still working on the 340. I’m a bit lost on what to do with it at this point, to be honest.

-glurk

I understand as we don’t get any solution so far. Well I can still modify some issues such as the double letter frequencies…the one I took assume that words have blanks inbetween which the 340 surely has not. ‘TT’, ‘EE’, ‘RR’ and ‘NN’ could get a better ranking then although none would exceed 30% I guess. I did do the calculation very carefully so I’m quite full of hope that further analysis with trigrams and reversal trigrams and/or vowel-consonant analysis could now bring us better results..not to forget, this cipher has way more homophones than the 408, which was even longer, too. Meanwhile, the ZDK program is running..it can solve the 408 in seconds – but not always – sometimes it doesn’t find the solution immediately. So it could be with the 340.

BTW, if you assume that it eventually could be a different cipher than the 408 – what type of cipher should that be? We can think about that, too. But Vigenere, for example, doesn’t work (symbols, not alphabet). So do simple substitution ciphers, Enigma, book cipher, Caesar, substitution, Playfair, ADFGVX, transposition…they all don’t use additional symbols for the chiffre alphabet. Some could still work, such as XOR or Skytale, however I see no clue that Z might have changed his encryption method that dramatically. Still possible, though.

QT

QT-

That’s a good analysis. I haven’t checked your math – WAY too much work for me right now – but I’m sure you are probably correct. The problem, as I see it, and I’ve mentioned this before, is that the 340 is probably NOT just a normal homophonic substitution cipher like the 408 was. So I’m not sure that all of this really helps… That said, I do enjoy reading your posts and I’m glad that people are still working on the 340. I’m a bit lost on what to do with it at this point, to be honest.

-glurk

I agree that the 340 is probably not a normal homophonic substitution cipher like the 408 and probably QT does as well. But I am thinking it is possible that the first stage of the 340 solves mostly as a normal homophonic substitution cipher, with a second stage employing a Caesar or something else. But before we get there we have to solve the first stage. Parts of this first stage solution may read like normal English language words and sentences and parts may read very strange until we discover the second stage to apply.

Long time no news here around..had to fight with a broken laptop, last file sadly completely gone. But now there is some news.

Some of us may have thought about the chances that three double symbols occur in a 340 cipher. Me too. And it is not enough to simply go for some probabilities of how often a double letter would actually occur in a normal text.

Because his statistical observation fades away with the usage of homophones. Therefore we got to review this issue under consideration of the amount of homophones Z might have used. Compared to the 408, by using 63 homophones, Z has in average increased the amount of homophones per alphabetical letter in the 340. We do assume, however, that he had used a similar (or identical) amount of homophones, nevertheless has increased the homophones in low-frequency letters. I do so because otherwise the statistical significance (later to be focussed on) would even grow higher.

Three main criteria are essential in the following consideration:

The amount of letters expected (overall frequency)
The amount of homophones
The statistical expectation regarding double letters.

Latter I have received from this list ( http://www.wordfrequency.info/free.asp?s=y ) which appears to be more precise (450m words). Indeed, it also covers the main 5,000 words, many of them might have been used by Z.

Let’s jump quickly into a preliminary example:

1. The letter Q, for example, is not frequent (overall frequency) nor frequent as a double letter (double letter frequency). Our double symbol which shows up three times is the ‘++’. Generally, ‘+’ alone has a frequency of 24, therefore Q can be ruled out for two (later even three) reasons:
a.) Q is not frequent enough as it should show up approximately 0.37 times only
b.) Q as a double letter (QQ) doesn’t occur in 5,000 words even once.
It therefore is most unlikely that ‘++’ is representing ‘QQ’.

2. The letter ‘E’, instead, is very frequent (overall frequency) and somehow frequent as a double letter (33 times in 5,000 words). It therefore could – on first view – represent the ‘+’ symbol.

However I will now demonstrate why this is not possible at all.

Please would you allow me a short introduction?
The main reason is that the statistical expectation of three double letters showing up, in homophone ciphers, is in advance being influenced by the amount of homophones. Assume that ‘EE’ would show up, let’s say, 200 times in 5,000 words. With an average length of 5 letters per word (assumed), we could now think about the 340 cipher consisting out of approximately 68 words.

This leads us to

200 / 5000 x 68

therefore an expectation of 2.72 times the ‘EE’ is present in the 340 (this amount is incorrect, in fact it’s much lower). Nevertheless, in fact it could be represented by the three (and this is crucial!) ‘++’ symbols.

BUT:
The letter ‘E’ is represented not only by one symbol. It is rather estimated that ‘E’ is represented by at least 5 or up to 8 different symbols! Even if ‘EE’ would show up three times in the 340, it is most unlikely that those three double letters – accidentially – are represented by always (3×2 times) the same out of those 5 to 8 different homophones! The very reverse, chances are even much greater that other homophones come into play to represent at least one or more symbols in those three expected double letters. Therefore even only one or two different double symbol would show show up in the cipher. This difference is significant as we do not only discuss the double symbols being present twice or three times in the cipher, no…instead we do understand that, assuming ‘E’ being represented by e.g. 8 symbols, the chances for ‘EE’ to be represented three times all by the same symbols is actually very low! It even is low for just the first double symbol!

Shortly described…the MORE homophones a letter is represented by, the LESS is the chance that a double letter (such as ‘EE’) would show up us a double symbol (‘++’) in the 340, too. Even less likely, that the following double symbols are existing of the same symbols.

So what to do? In fact, we do already talk about combinatory mathematics. Everybody of us does know the chance to throw a dice to a 6, which is, throwing once, 1/6. This is easy. But what we’ve got here is way more complicated:

Scenario 1:
Imagine 16 balls in a bowl…with 8 different colors (two each – representing the double letter – and the 8 colors representing some 8 different homophones). We are now allowed to draw 3 times (representing e.g. the expected 2.72 double letters (‘EE’)). Now guess how low is the chance that you draw three times after another ALWAYS the SAME COLOR for BOTH BALLS. In this scenario, not even one ball would be allowed to have a different color. This most likely won’t work, even if you may want to try it at home with your kids.

Scenario 2:
Imagine 2 balls in a bowl only, both of the same color. This would be the case if only one homophone existed for the letter, therefore ‘+’ representing a letter such as Z. Then we definitely get the double homophones all being the same, without any problems. But what is the issue now? First, the letter Z usually doesn’t occur 24 times in a 340 cipher. Second, with only 9 times in 5,000 words it is a bad candidate for showing up three times as a ZZ in a 340. Although ‘everything is possible’, this scenario is even less realistic than our first one.

Scenario 3:
The favorite…what if the amount of homophones (colors of the balls in a bowl) is quite limited, e.g. to three different homophones, AND the expectation of the letter to occur as a double letter is quite high, e.g. 7 times? And in addition to that, let this letter be even a medium to frequent one, too?

All those scenarios above can be calculated.

We therefore are able to say which letter (based on a certain number of assumed homophones and certain assumed double letter frequencies) is the most likely to be represented by three double ‘++’. In the beginning I thought this would be easy to calculate, but I soon realized that it is actually not. Mainly because we got two criteria of ‘balls’ to be drawn, the first double letter symbol and the second one (thus drawing two balls at the same time with the goal for them having the same color). This is circumstantial as we can write down all those combinations even manually down on a piece of paper in form of a probability tree. To make that easier, however, there is the great Bernoulli method to evaluate those chances considered above. Those, however, are still depending on the amount of homophones.

An example:
Let’s assume two homophones for one letter, the symbols A and B. Therefore a double letter can be represented by AA, AB, BA or BB. The chance to get an AA is 0.25 or 25%, same with BB and the others. To get a 3 times in a row ‘AA’ situation is therefore 0.25^3 or 1.5625%. This might be doubled as we are completely satisfied with three BB’s, too (however we don’t expect BAs and ABs hanging around..maybe additionally but that again is against our double letter frequency expectation).

Probabilities for getting an ‘AA’ situation are:

1 homophone: 100% – AA
2 homophones: 25% – AA, AB, BA, BB
3 homophones: 11.11% (1/9) – AA, AB, AC, BA, BB, BC, CA, CB, CC
4 homophones: 6.25% (1/16) – AA, …, DD
..
7 homophones: 2.04% (1/49) – AA, …, …, GG
(every homophone may be combined with every other homophone, therefore e.g. 7×7 in the latter example)

If we now have look at the ‘E’, with – let’s now say 7 – homophones, this is getting different: 1/7 = 0.14285^3 = 0.00291545 or approximately 0.3%. This is simplified, as we only deal with three draws to get those identical double letters in a row.

But what if out of 7 draws, no matter when, 3 identical pairs of homophones show up? What are the odds then?

Great Bernoulli developed a formula for shortening up this tree of probabilities. It can be tested on both, a low and a high numbered basis, and does go like this (German link: http://www.mathe-online.at/lernpfade/Ko … ?kapitel=4):

With

n=number of ‘tries’ (expected double letters of a specific alphabetical letter in a 340 cipher text)
i=number of ‘successes’ (the required three double symbols present in the 340 cipher text)
p=probability of success (the odds of e.g. getting an ‘AA’ instead of an ‘AB’ or ‘AC’,..)

Putting it into the formula, we simply get the probability of how likely it is to get three double symbols at all. This we can do for each alphabetical letter seperately. Beware: We now do assume a certain amount of homophones for each letter, too, so the chances (‘p’) is differing for each individual letter of the alphabet, fully depending on how many homophones are expected to be represented by.

I did make a tableau consisting of ‘overall letter frequency’ & ‘amount’, ‘double letter frequency’ & ‘amount’ and went into the possibilities of getting an ‘AA’ situation which shall depend on 2, 3, 4 etc. homophones. In my excel sheet the formula for each alphabetical letter looked somehow like this:

=FACULTY(G3)/FACULTY(3)*IF(H3=3;P$3^3;IF(H3=4;R$3^3;IF(H3=2;N$3^3;IF(H3=1;L$3;IF(H3=7;T$3;fehler)))))*((1-IF(H3=3;P$3;IF(H3=4;R$3;IF(H3=2;N$3;IF(H3=1;L$3;IF(H3=7;T$3;fehler))))))^(G3-3))

which should be no more and no less than the Bernoulli formula (the ‘if’ refers to the different amount of homophones expected).

I have to admit that I was suprised:

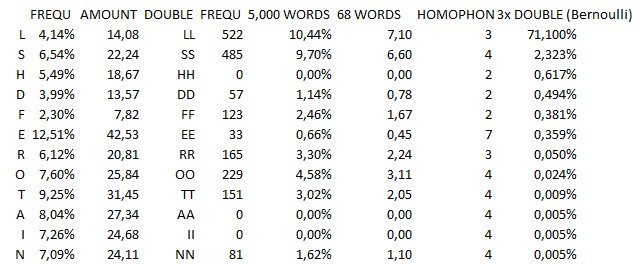
1. Three letters showed up with an ‘error’ as I had not yet defined the precondition of ‘0’ homophones, e.g. Z, Q, J. Didn’t take much care about those.
2. All letters with only one homophone expected showed up with a different error (because the square in Bernoullis formula gets into zero or negative), those were the letters PCMGBZUJKQVWXY. All those letters have an overall expected frequency of 0.09% to 3.06%, therefore would most of them not even be considered to show up more than 10 times (as double and single letterS) – please reconsider: The ‘+’ is present 24 times. Therefore those letters didn’t even reach 46% of what ‘+’ is coming up with. Also none of those letters is expected to show up even twice (therefore not even three times) as a double letter.
3. The letters LSHDFEROTAIN, however, went into a closer Bernoulli-consideration: Those letters gave values on what the chances are that they would show up in the cipher with three identical double symbols.

And guess what:

This is the result. Both, depending on a certain amount of homophones as well as oncertain double letter expectations (latter one based on 450m words). It is the statistical expectation for a letter to appear three times as a double symbol in a 340 cipher.

EVEN IF we assume e.g. the letter ‘O’ to show up with four different types of its homophones (therefore satisfied not only with AA but also BB, CC, DD), the probability doesn’t even increase above the benchmark of 0.1 percent (0.024% x 4 = 0.096%).

Why is that? Why is this so low?

Well that’s explained quicker than what I had written above:
‘O’ is expected to show up only 3.11 times as a double letter (‘OO’). And, due to it’s overall letter frequency, it is expected to have 4 homophones. To draw three times two identical balls at the same time out of a bowl with 8 balls (with putting them back), all of those being colored colored the same, is simply extremely hard.

With 71% it is obviously way easier to draw 7 times, with three colors in the bowl only, to get three times a pair of two identical colored balls (or symbols). It is, imo, not possible to follow that thought ‘immediately’ as such a drawing of balls could look like this (or completely different..many ways, seven levels):

AC, BB, BC, CA, BA, CB, BB, AA, BC, AC, BB

As you can see, in this example it took us 11 draws to complete the three double homophones.

And this is exactly what the table above had told us:
It is not enough to draw 7.1 times and expect three double ‘LL’ symbols. Instead even 10-11 draws are expected to be needed to get those three identical symbol double patterns in the ciphertext.

Accidentially, in the 340, 7.1 draws (occurrances) were enough. Or had Z used the double letter ‘LL’ not only 7.1 times but 10 or more times in his cipher?

What is a fact, however, is that due to a higher amounts of homophones (caused by a higher overall frequency of the letter) and due to lower expected amounts of double letters (e.g. the ‘DD’, which is rather seldom compared to ‘LL’), the other letters do not (significantly!) come into consideration to be represented by the three double ‘++’ symbols.

The first solved symbol, therefore, imo based on valid, significant statistical data, is therefore the ‘+’ representing the consonant ‘L’ (and only that one, as long as no error or absolutely extreme outliers exist).

It should be mentioned, however, that assuming different amounts of homophones (higher ones) would even reduce this probability (lower ones would increase, however the 340 has more, not less homophones). ‘LL’ to occur three times in the 340 is not even expected at all. This would actually requre a value of 100%. Instead it’s 71%. With Z using ‘LL’ a bit more often or the symbols accidentially falling into a good pattern, the triple (definitely exist more in the cleartext) ‘LL’ represented by the triple ‘++’ is, as far as I can say, the only correct solution.

QT

IMO this is excellent work QuickTrader! And not only is LL a combination that occurs often in normal English language usage, the Zodiac in particular used the LL combination more than any other. look at this past work for reference, with comments from myself, glurk and doranchak. In terms of solving the first stage of the 340, I agree with you very much that as a working hypothesis it makes very strong sense to solve ++ as LL.

AK Wilks:

In the first Zodiac Code he used "S" 24 times. Only once was there a "SS", and that happened in the phrase "it iS So much fun". Zodiac neved used a word that has "SS" in it, not once. Compare that to the number of words he used in the first code that had "LL" – SEVEN different words! And they are words we might think it is likely he also used in the 340 code. They were:

Zodiac also used these words with a single "L". – like, people, wild, girl, slaves, slow, animal, afterlife.

By my rough quick count, the letter "L" appears 33 times in the 408 code. About 8.1% of the letters are "L", which is about double normal usage, as it happens that many words Z liked to use have either L or LL in them. So if Z used "L" 8.1% of the time in the 408, it seems to me that 9.7% use in the 340 code is within normal deviation, really only two more uses of a word like kill, killing, collecting, etc., would do it. And if we strike the untranslated last 18, leaving us 390 translated letters, the 33 uses of "L" amount to 8.5%, which is even closer to my proposed 9.7%. in the 340 code.

GLURK: I’ve done a small bit of work on this, and I’m going to have to say that as far as Zodiac’s use of the doubled letter "L," he did in fact use it a lot.
More than would be expected in normal writing. Even in words that, properly spelled, would not have the letter doubled.

I did not do exact word counts, sorry, but in a quick study I’ve found:

ALL, ALLREADY
AWFULLY
BILLIARD
BILLOWY
BULLET
BULLSHIT
CALLED
CELLING
COLLECT, COLLECTING
CONTINUALLY
FILLING
FULL
HELL
HILL, HILLS
HOLLY
KILL, KILLED, KILLER, KILLING
PULLED
REALLY
ROLLED
SHALL
SMALL
SQUEALLING
TELL, TELLING
THRILLING
TITWILLO
UNTILL
VALLEJO
WACHAMACALLIT
WALL
WELL
WILL

This should be all of them, I think, unless I missed something… I probably did miss something…
I don’t, however, believe that the 340 is simply a homophonic cipher like the 408. But I also don’t have any doubt at all that Zodiac often used "LL" in his writings. He clearly used it more than would be expected.

DORANCHAK: Here are some others:

ALLEY (confession letter)
ALLEYS (confession letter)
ALLWAYS (1971-03-13-times)
BALL (confession letter)
BELLI (1969-12-20-melvin-envelope)
CALL (confession letter, 1969-11-09-chronicle, 1970-07-26-chronicle)
CELL (1970-07-26-chronicle)
FALL (1970-06-26-chronicle-cipher)
FELLOWS (1970-07-26-chronicle)
FOLLOWED (confession letter)
UNWILLING (desktop poem)
SPELL (1974-02-14-sla)
SPILLING (desktop poem)
WILLING (confession letter)
WILLINGLY (confession letter)
YOULL (1970-10-05)

Is it possible that this cipher could be a Vingiere cipher with a Caeser shift?

If that were the case then it would negate the effectiveness of distribution frequency analysis.

Based on the card that the Cipher was enclosed with perhaps the Key Word was "Thing" and if we multiply Thing x4 we would have a good explanation of the 20 rows in the 340 with Thing repeated 4x then codes to be adjusted by the letter value of T=20 H = 8 I= 9 N =14 G = 7

We also see Thing underlined 6 times with 6 exclamation points and we know 6×6 =36 + 26 = 62. Is it possible that the shifts don’t happen alphabetically but on a Typewriter keyboard?

For example in Line 1 H + 20 = B or N depending on the direction. if we add twenty to H we get B or N depending on which direction you go. Then 6 spaces on the Typewriter keyboard would yield a shift key or backspace each of which would carry a numerical value assigned by placement on the typewriter based on location. 54 keys on some old typewriters.

I know sounds a bit convoluted but it seems that given the struggles with frequency that Z must have chosen a system that would guard against frequency analysis and cribbing.

Those are all good posibilities. I think Z left multiple clues of 3-6-9, including the ones you mention, plus the +09 that keeps showing up in the 340, the 0-3-6-9 on the map he sent in and others. I think that could be clues for a 0-3-6-9 Caesar shift in the second stage of the code. But before we get there we have to solve the first stage.

I think Quicktrader has shown an excellent analysis of why LL is likely to recur more than EE, OO or anything else. And the comments from me, glurk and doranchak show that Z specifically used LL more than any other combination. For all those reasons I agree with QT that it makes sense to provisionally solve the ++ as LL.

Using the excellent analysis by Quicktrader showing the ++ very likely solves as LL, and from Glurk and the FBI files that normal F and normal B possibly solves as L, this is what we get:

Building from that, as Graysmith also solves + , F, and B all as L, I then add in strong logical possible word solves from the Raw Graysmith of SEE A NAME and THESE FOOLSHALL SEE this is what we get:
Note: I did not intentionally create the 1st line THE or the 2nd line HELLTOO. Those were cteated by applying the QT solves, the Glurk/FBI solves and the RG word solves of SEEANAME and THESEFOOLSHALLSEE.