i’d put my money on what daikon said about z not being meticulous or patient. i think your work shows he did at least two things – likely homophonic substitution coupled with some other method. the "other method" is likely to be something done quickly with elementary knowledge of encoding techniques. daikon’s thoughts on him literally cutting up the cipher by column and rearranging it mirrors exactly the kind of methods we see in his writing. hurried, self-aggrandizing, but not really substantively difficult. i get that the 408 took lucky guessing and years for a computer to be able to reliably decrypt, but is that because it was a difficult technique for him to master or more because any method that has a short ciphertext relative to the number of symbols in its key is inherently difficult to crack?

also, thanks to all of you who answered my questions about bifids in the other thread too.

@doranchak, I’m not sure how big the google word level dataset is but perhaps you can convert the words to numbers and then just have an array which holds the word for each number. That could possibly save allot of memory.

Looks like all the 1-gram files add up to 5.3 GB of compressed files. I imagine that will be rather large when unzipped to plain text. But maybe we would only care about a top percentile of them.

Things get really hairy when you go up to 2- or 3-grams. For example, the compressed file for 2-grams starting with "th" is 4.4GB compressed. I think even a good sampling of the most popular 2-grams would still be quite large.

Just for fun I checked the file size for the compressed file of 3-grams starting with "th". It is 80 GB. Yikes!

It’s a nice "big data" challenge.

I think having such a database of popular word-level n-grams available would be very handy for the manual phase of solving the cipher. For instance, you could have a partially solved plain text with no word breaks (a result of zkdecrypto or azdecrypt), and the user could be shown close matches of phrases from the corpora. Word combinations that score highly will appear in the top of the list. Then the search can be refined to produce the selection of crib phrases that maximizes the appearance of other highly-ranked phrases within the plain text.

There is also the chance to find high-scoring phrases directly from such a large database. If you look at sections of cipher text, if there are enough repeated symbols within that section, then the probability of accidentally matching a full phrase is very low. So, looking up phrases, subjected to those constraints, from the huge database should produce high-probability matches (in theory). There could be two contributions to the scoring of such matches: 1) the likelihood of an accidental match, and 2) how often the matched phrase occurs in the English language.

It’d be kind of like when Google suggests ways to finish your search terms, except it compares the candidate phrases to the snippet of cipher text, to test if the constraints are violated (such as: "the 3rd, 10th, 17th, 18th, and 30th letters in this phrase are identical" or "the bigram at position 4 repeats at position 10", etc)

Of course, this would only be useful for simple substitution ciphers. And I think it’s only practical if you have a really fast way to index this humongous dataset.

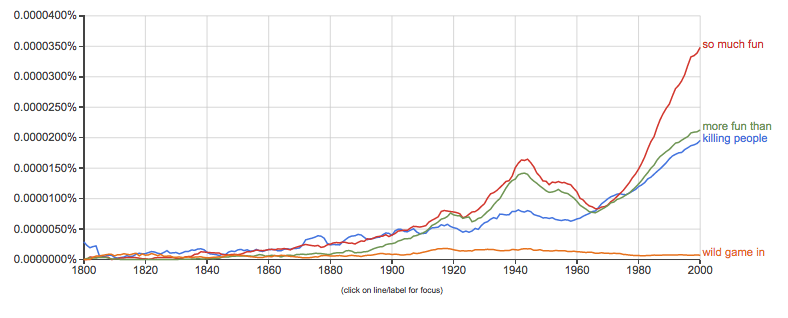
Here’s a way to visualize the ranking of n-grams, using real snippets from the 408’s solution: https://books.google.com/ngrams/graph?c … in%3B%2Cc0

About columnar transposition (for a 17×20 grid). I’ve done some work on this. I don’t think it’s actual after homophonic encoding …

Wait, why would it matter if the transposition was done before or after homophonic encoding? The result should be pretty much the same, with the exception of the homophone cycles being destroyed in the ciphertext if the transposition was applied afterwards.

Somewhere at the end of last year I wrote a secondary hill climber for columnar transposition w/o any additional intelligence. I was able to retrieve columnar transposition for up to 10 columns with a searchspace reduction factor of about 3 or 4. Not very impressive, the problem is that it’s very hard to hill climb, the solution is very spikey. It’s sits on a telephone pole in hill climber terms.

I bumped into the same issue! With any optimization algorithms, be it hill-climb, or simulated annealing, etc., you want the solution field to be as smooth as possible. In case of a columnar transposition, when doing the hill-climb, you only want to swap the adjacent columns. Reason being, it only changes the adjacent letters in the solution, so it touches/affects much fewer N-grams compared to changing columns that are far apart, so it will change the overall score much less. I also did a test with my own cipher with columnar transposition, and when I had my SA solver swap random columns, it couldn’t converge on a solution once I went past 6 columns, I think. But when I restricted changes to only adjacent columns, it managed to solve ciphers with a couple columns more, up to 8, I think.

I already talked about the smoothness of the solution field before regarding a cipher with a relatively high-frequency symbol (such as ‘+’ in Z340). Hill-climbers, and SA-based solvers as well, tend to have hard time with such ciphers (i.e. they require more restarts to converge to the correct solution), because changing that high-frequency symbol hugely affects the score, because it changes a lot of letters in the solution. So the solution field has a distinct roughness, or a "wall", along that high-frequency symbol, which the solver hangs up on, so to speak.

I’m not sure if higher order n-grams will help much.

It should help avoid the issue of the solver converging on the solution that scores higher than the correct solution. Basically, you need a much better LM (language model), once you start randomly shuffling letters around, or you end up with a lot of anagrammed nonsense similar to the multitude of proposed "solutions" you see on the Internet. We might even have to start using word N-grams, which scares me. 🙂

Some ideas that I have, is to implement a special anagram algorithm to the rows and combine scores. Another one is to use some form of skip-grams, where not every letter has to be a match.

That’s actually how the Beam Search algorithm works. At its core, it does what a human would do when solving a cryptogram, which is why I had such high hopes for it. You start with all cipher symbols unassigned (i.e. unknown). Then you pick one of the symbols and try to plug all possible English letters. You end up with 26 partial solutions (one for each letter), with lots of empty spaces (for unassigned cipher symbols). Then you pick another symbol and again plug all possible letters, separately for each of the previous partial solutions. You end up with 26 * 26 partial solutions. Now hopefully you picked your symbols in such a way that you have some bigrams in the partial solutions and you can score them according to their frequencies. You repeat the same with the third symbol and so on. Each time you score the partial solutions based on the available N-grams. If you only have a non-interrupted bigram, you use the bigram table, if you have 3 letters together, or a 3-gram, you use 3-gram table, and so. Basically, you always use the highest available N-gram table for each uninterrupted string of letters. Now, if you keep doing that as I described so far, you’ll end up brute-forcing all possible keys, which is obviously going to take a very long time. So the trick is, you only keep a number of the top partial solutions at each step. That number is called the "beam width", and you need to adjust it based on the multiplicity of the cipher. For lower multiplicity ciphers, such as very long ciphers, or 1-to-1 substitutions, you can get away with perhaps only 1,000 top partial solutions. For higher multiplicity ciphers, you need millions. Malte Nuhn claims that they had to use the beam width of 10M to algorithmically solve the 2nd Beale cipher, which has an even higher multiplicity then Z340.

Here’s my problem with the Beam Search method though, and why I can’t see how it can solve higher-multiplicity ciphers without luck being the deciding factor, or a lot of manual analysis beforehand. To get even remotely reliable scores for the partial solutions, you need to get at least a few separate 5-grams in the partial solution. Which means, you’ll need to assign at least 5 separate symbols, and keep at least 26 ^ 5 = 1,1881,376 top solutions. And you have to be very smart about which symbols you choose to expand and in which order. I’ve implemented Beam Search, and when I tried to get it to solve Z408, it was getting nowhere with 10M beam width, no matter which expansion order I chose (and I even tried random order). I’m sure after careful manual analysis of which symbols to pick first, or cheating by using hindsight and picking the symbols for "KILL", I can get it to solve Z408, but that would be, well, cheating.

Math is supposed to be a universal language right? Often, what is actually going in is not difficult at all, it’s just in another language.

Yes, you are correct, it’s just another language of sorts. But the thing is with math, it often relies on a lot of prior knowledge. For example, when you see the phrase "we use the Noisy Channel approach with Gibbs sampling over Hidden Markov Chain Model and Viterbi Algorithm to choose the plaintext decoding p that maximizes P(p)·Pθ(c|p)^3, stretching the channel probabilities.", what does it mean? You can look up all individual "components" of that phrase, but it will involve even more unknown terms, which you’ll have to look up as well, and deeper and deeper it goes. Unless you want to spend weeks learning (or re-remembering) the whole related field of science, you’ll likely need to do a Beam Search on that phrase to get to the bottom of it. 🙂 With programming (i.e. looking at just the source code), there is very limited prior knowledge involved. You need to know about loops, arrays and variables, and that’s pretty much it. 🙂 If the source code is clean and un-optimized, and well commented in especially tricky places, you won’t need to learn anything else before you can understand what it does.

I’ve been thinking about that problem, too, especially when considering Google’s humungous n-gram datasets

Using word N-grams would be awesome, but as you pointed out, the memory requirements are just astronomical. You do already get to use the word-level 2-gram stats if you go beyond letter-wise 4-grams. The reason is that the average length of English words is between 4.7 and 5.1 (depending on who you ask, and what corpus they used). Which is why you generally get a good improvement in quality of automatic solutions if you start using 5- or 6-gram stats. Your frequency counts now span more than one word on average, and you get the advantage of word-level 2-grams and even 3-grams for shorter words, so meaningful sequences of words start to get much higher scores.

I also wonder about compressing the ngram data in RAM. A byte can hold 256 different values but we only care about 26 different values of a letter of an ngram. Can we apply something like modular arithmetic to encode more than one letter per byte?

You don’t actually need to store the individual N-grams in memory if you use an N-dimensional array. I.e. for 2-bigram stats, all you need is an array of 26*26 frequencies (or, rather, logs of frequencies). To get the frequency for, say, "BC", you just take 2gram_freq[2][3] (i.e. in a table, it would be 2nd row for ‘B’, 3rd column for ‘C’). No need to store the actual "BC" string anywhere. Same for 3-grams and so forth. For higher-order N-grams, it’ll probably be better to store the data as a long list, as Jarlve is/was doing, then it might make sense to start using bit-fields to store letters, as you are proposing.

Have you contacted the authors? They are often glad to share.

I was thinking about it. 🙂 I don’t know how they would feel about someone emailing them out of the blue and asking to share their source code. I might have to start with simple questions, and see how it goes.

would it work to use word n-grams of words he was more likely to use? you could probably eliminate a significant percentage based on an analysis of his writing level.

would it work to use word n-grams of words he was more likely to use? you could probably eliminate a significant percentage based on an analysis of his writing level.

It’s an interesting idea, but the problem is that we don’t really have a very big corpus of Zodiac texts, so we can’t really be sure about his vocabulary. I actually have the stats from his letters (I only included the ones that are very likely his, and skipped a few that are only "possibly his"). I have 1,018 distinct words, and out of those he used only 386 words more than once. Which means 62% of the words were only used just once, so we can’t be sure if they are in his normal vocabulary. 386 words is way too small to be representative. What’s the technical term? Statistically insufficient sample?

Interestingly enough, Zodiac’s most frequently used word is, as expected, "THE", however his 2nd most frequent word is "I". Looking at English word frequencies, the word "I" is actually 11th. "MY" is Z’s 10th favorite word. It is actually 44th for an average text. Hardens were correct to guess that he liked to talk about himself a lot. 🙂

Wait, why would it matter if the transposition was done before or after homophonic encoding? The result should be pretty much the same, with the exception of the homophone cycles being destroyed in the ciphertext if the transposition was applied afterwards.

Because the encoding has its tendency to create bigrams in its direction. On average there should be less bigrams in the cipher if the transposition was done after encoding. At least that’s what I observed a while back. It’s not conclusive though, since it also relates to extent of the transposition.

would it work to use word n-grams of words he was more likely to use? you could probably eliminate a significant percentage based on an analysis of his writing level.

It’s an interesting idea, but the problem is that we don’t really have a very big corpus of Zodiac texts, so we can’t really be sure about his vocabulary. I actually have the stats from his letters (I only included the ones that are very likely his, and skipped a few that are only "possibly his"). I have 1,018 distinct words, and out of those he used only 386 words more than once. Which means 62% of the words were only used just once, so we can’t be sure if they are in his normal vocabulary. 386 words is way too small to be representative. What’s the technical term? Statistically insufficient sample?

Interestingly enough, Zodiac’s most frequently used word is, as expected, "THE", however his 2nd most frequent word is "I". Looking at English word frequencies, the word "I" is actually 11th. "MY" is Z’s 10th favorite word. It is actually 44th for an average text. Hardens were correct to guess that he liked to talk about himself a lot.

i agree entirely with your assessment of the words he used in his letters. i was thinking more along the lines of analyzing his word usage to determine what reading/writing level he exhibits. if he is, say, safely in the "eighth grade reading/writing level" then we can develop a corpus of words that meet that criteria which should eliminate a large percentage of all of the words in the natural english language. e.g. – i’d be willing to bet the cipher doesn’t contain the words "copious", "banal", "obsequious", etc (all twelfth grade reading words).

it may be a fruitless endeavor but i’d be willing to undertake some analysis if a positive end result would be beneficial to the cause.

the idea reminds me of randall munroe from xkcd’s book, the thing explainer, that only uses the top 1000 most common words in the english language to describe technology.

After seeing doranchak’s post about a new Gareth Penn cipher I did a Google search for him and eventually found this page: http://www.zodiackillerciphers.com/?p=179

There is an image of numbers in a matrix which could be used for transposition in a grid. The distance between following numbers is often 19. The 340 bigrams peak at a period (distance) of 19! It is not normal for a cipher to show a significant peak at a distance so great. That got me thinking, is this it? Anyone know more about this image? I tried to recreate a numeric form of the matrix thinking that it was just numeric shift using its length (441) as a modulo but the numbers came out different.

The numbers aren’t a code but just an offset grid of the numbers from 1 to 441. Move 2 to the right and up one for the next number in sequence. Could this be used in a transposition encoding?

So yes, move 2 to the right and up one for the next numbers in sequence. And when you go out of bound of the cipher wrap it around to the other side. But this creates problems as at some point you’ll run into an old number, so the author then decided to go down one spot and continue the process. So there is at least one extra rule necesarry. When applying this scheme with a straightforward numeric shift distances that are prime numbers, not even or a factor of the grid are the way to go or otherwise you’ll run up into old numbers. So the author of the matrix seems to have been aware of that as he used a distance of 19. But then did it different?

In the image you’ll see that after 21 the author runs into 1 again and just places 22 one spot down below 21 and then continues the process. Would such a scheme also be more prone to create pivots? It has a really interesting coincidence with one of the stranger (out of place) observations for the 340.

So yes, move 2 to the right and up one for the next numbers in sequence.

I might be mistaken, but there is an easier way to read this matrix. As displayed, it has the width of 21. If you rearrange it into a matrix of width 19, it will be as easy as reading it "columnary": by columns, just starting in the middle (where 1 is) and going up. You’ll have to step down 2 rows and move 2 to the right for each subsequent column though.

I think it’s different. Because the author ran into his old numbers at some point and introduced a new rule.

Well, if you read a matrix by columns you’ll do the same for each column, if you wrap around the edges. This matrix appears to describe a regular columnar transposition of width 19, read bottom to top, with the key: 15 6 16 7 17 8 18 9 19 10 1 11 2 12 3 13 4 14 5. The only quirk is the starting point (first row and then you go up), and there is a two row shift down when going from one column to another (i.e. when going to the next column, you start reading it from the character 2 rows below the previous).

Jarlve-

Regarding that grid you posted above, I REALLY don’t think it has anything to do with ciphers or transposition. It is a "magic square" like the (different) one Gareth Penn created in "Times 17":

"A magic square is a square divided into a number of smaller squares. Each of the smaller squares contains a number. When all of the numbers of each row, each column, and each of the two major diagonals are added up, you get the same sum every time."

Penn even explains how to create one. It’s also the background on the cover of the book. His is 17 x 17 of course,

They are interesting things unto themselves, but since there are infinitely many of them possible, I don’t think trying to apply them to transpositions would be very helpful.

-glurk

EDIT: doranchak made an online tool to create these, see here: http://zodiackillerciphers.com/gridmaker/

EDIT: doranchak made an online tool to create these, see here: http://zodiackillerciphers.com/gridmaker/

That’s cool! I wasn’t aware of it.

Whatever it may be I still can’t get it out of my head that it coincides with the bigram peak at a distance of 19 in the 340. I’ve already tried various ways of untransposing the 340 in this manner at all possible offsets (offsets don’t really matter if no secondary rule) and distances. A solution was not found but the examples with a distance of 19 scored slightly higher than the other distances (they were on top). Maybe something is there or more bigrams = higher score.