QT —

Are you assuming that the 340 is not a transposition cipher? I would think that if the 340 was like the 408 that one of the other decryption methods would have nailed it.

There is already an implementation of Aho-Corasick here.

I’m willing to work on the decryption problem, just need to understand more about the proposed process.

Anybody an idea of how to check dictionary entries against any text by using Python and, ideally, by using the Aho-Corasick algorithm in Python? Any idea is welcome..

I would have one or a couple of arrays, lists which hold words sorted by length and then by alphabet. And then check the searchstring for the longest words first, and when they are found mark these parts in the searchstring as locked. Generally, when comparing one list versus another the computer has to go through the list one by one.

Example searchstring: "iamcollectingslavesfortheafterlife"

Found collecting: "iamCOLLECTINGslavesfortheafterlife"

Found afterlife: "iamCOLLECTINGslavesfortheAFTERLIFE"

Found slaves: "iamCOLLECTINGSLAVESfortheAFTERLIFE"

Found forth: "iamCOLLECTINGSLAVESFORTHeAFTERLIFE"

And here we run into a problem with the approach I just suggested. Because it reads "for the" and not "forth e". So better would be to generate a series of probable word matches and score these with word-grams. An excellent example of this http://quipqiup.com/

QT —

Are you assuming that the 340 is not a transposition cipher? I would think that if the 340 was like the 408 that one of the other decryption methods would have nailed it.

There is already an implementation of Aho-Corasick here.

I’m willing to work on the decryption problem, just need to understand more about the proposed process.

Thank you for the link.

A transposition is quite unlikely as it usually would transform alphabetical cleartext letters to alphabetical cipher letters and vice versa (A-Z <> A-Z). How would you transposite multiple homophones on letters? Regardless of how this would be done, it then would be a homophone substitution (A-Z <> Homophones). It appears to methat the 340 is similar to the 408 with one main difference: The homophones have not been used in a specific order:

1st, 2nd, 3rd,…1st, 2nd, 3rd,…

but have they been used irregularly:

1st, 2nd, 3rd,…2nd, 3rd, 1st,…

As there are no or at least not many repeating sequences, the sequential analysis fails. This must not be necessarily true for the whole cipher, but if you look at certain homophones, e.g. the ‘w’ symbol, you can see that those appear only in certain areas of the cipher. Some homophones show up rather in the 1st third, others in the second or the in last third of the cipher. Such homophones could in fact be ‘relatives’ representing the same cleartext letter.

In the third part of the 408 this behaviour was similar, however it had solid structures in the beginning (e.g. letter ‘E’ repeating with 7 homophones in a row a few times). It therefore was solvable by methods of sequential homophone analysis. The non-sequential use of homophones plus a shorter cipher text plus more homophones make the 340 so hard to crack. Sequence analysis methods wouldn’t work as there are no or at least no longer sequences to rely on. It seems as if the only way to solve it is to focus on the structures inside the cipher itself, the way the homophones are connected to each other (e.g. n-grams).

Of those structures there are many bigrams etc but not even one single 4-gram. However we’re lucky with other double letters and the two repeating trigrams which are connected to each other (‘IoFBc’). These structures deliver enough material to create an array of strings that can be analyzed.

QT

Thank you both for jointing this topic..Jarlve, you’re correct with searching for a longer word first. Based on the cipher structures, it is possible to create an array of strings (which I call FCCPs) that can be analyzed for words. The length of the string is given according to how many homophones you choose. Using all at the same time would end up in 55^26 variants, impossible to calculate. Choosing four homophones only in general ends up with a string that is too short to analyze. Finding a string between 8-15 letters is better to analyse, especially if there can be found multiple words in it.

To approach with a long word first is fine, especially if a second word can be found, too. With Aho-Corasick it is much easier, however. It delivers all pattern solutions simultaneously, thus does not ignore any possible solution. It tells us if e.g. zero or up to 5 words can been found in the string. And it also tells us their position inside the string.

It is also quicker than any other method to compare an dictionary with a text. Setting up the criteria on finding two words, one with Length > 4 and one with Length >5 should deliver all potential solutions. Your point with ‘locking’ is a good one, I had received problems when doing similarly with excel (it found two words..WHO and WHOSE although it apparently was only one word.

QT

QT-

Just to test your idea, can you create a homophonic cipher similar to the 340 that my ZKDecrypto, or Jarlve’s AZDecrypt CANNOT solve?
Because I (among many others) am fairly certain that if the 340 were a normal homophonic like the 408, it would have been solved ages ago.

-glurk

QT-

Just to test your idea, can you create a homophonic cipher similar to the 340 that my ZKDecrypto, or Jarlve’s AZDecrypt CANNOT solve?
Because I (among many others) am fairly certain that if the 340 were a normal homophonic like the 408, it would have been solved ages ago.

-glurk

Hi Glurk,

your tool works perfectly..but do you know if it can handle 340 ciphers with 55 mixed homophones lacking of any sequences, toos? You are right when you say that it would have been solved. What I believe is that Z had differed the substitution to the extend that there are no sequences. In the first encryption, the 408, he had used one homophone after another, repeating their order. I doubt that he had done so in the 340, he rather took any homophone out of the letter’s homophone group. It is even likely that he structured them according to how far he had proceeded with the encryption, e.g. used the w symbol not earlier than somewhere in the lower third of the cipher. This makes it very hard to find repeating sequences for any software tool.

By the way:
The tool is already running. I can now add dictionary entries and search the strings for them. Thus a list of cleartext phrases is printed if one (so far..) of the dictionary entries is found. Could not implement the Aho-Corsick algorithm, however it works quite well with this

Lex = ("rat", "rat,...)
chain = C+kl+pl+F+l+w+B+I+ö+L+pl+pl+ö+w+C+z+w+c
if any(x in chain for x in lex):
    print (chain)
else:
    print ("no strings found in chain")

The code alone doesn’t alone as no definitions for C etc. has been made in this example, but on my Python it already works. To check a dictionary of five words only on 3,000,000 strings (FCCPs) takes about 18 seconds. To check those five words on all possible strings would take approximately half an hour. And not even using Aho-Corasick, yet.

QT

Quicktrader, it seems as though your are having a lot of fun writing your new computer program. I have a new spreadsheet that generates homophonic substitution messages and I can randomize the selection of symbols that all map to the same plaintext when encoding. If you are interested and want to test your new program, let me know and I will volunteer to make a message like the one you are talking about, including making sure that there are a few double symbols like the ++. Smokie.

Quicktrader, it seems as though your are having a lot of fun writing your new computer program. I have a new spreadsheet that generates homophonic substitution messages and I can randomize the selection of symbols that all map to the same plaintext when encoding. If you are interested and want to test your new program, let me know and I will volunteer to make a message like the one you are talking about, including making sure that there are a few double symbols like the ++. Smokie.

That’s great, thanks for the offer..would like to try on it (guess Glurk’s tool works on those, too?).

I have now added a dictionary with approximately 2,000 words of length >5. Only searching for one word, so far. To check all strings takes approximately 21 hours of computation (based on + = L and looking for the five most frequent 5-grams). Wish I had a faster pc D

QT

UPDATE:

Program is working..all strings with words >5 letters pop up one after another..still not perfect but basically it’s ok:

Few seconds later:

QT

Here is a message with 62 symbols, strictly homophonic with no other cipher steps, non-cyclic encoding and four occurrences of "LL" which is symbol 30.

32 22 15 47 12 11 27 9 37 32 51 14 15 33 32 39 5
16 2 37 62 39 18 55 21 12 33 27 36 27 38 28 23 15
4 45 52 5 57 32 52 22 31 45 31 59 4 51 3 37 62
2 33 41 57 37 54 39 17 6 47 25 19 22 55 37 14 51
49 1 36 10 10 2 44 29 38 31 51 48 18 2 27 45 26
16 50 2 37 10 20 42 6 30 26 35 48 62 42 56 45 33
41 55 21 13 47 30 26 28 16 9 19 40 7 30 27 37 49
2 48 60 16 30 30 22 42 6 19 41 7 30 26 38 50 7
56 19 4 7 42 39 51 55 21 13 18 31 36 40 9 12 47
31 31 52 23 13 18 40 30 30 12 53 55 25 59 27 53 24
32 23 16 27 45 7 56 54 52 12 47 17 30 62 60 25 35
20 51 48 23 31 29 37 13 60 53 24 12 34 2 30 30 51
40 59 31 19 1 58 31 61 41 56 4 43 27 30 16 42 17
43 27 8 54 56 47 14 5 41 42 29 48 50 2 52 11 41
60 36 42 35 54 24 13 46 56 19 7 15 49 26 9 14 61
41 56 1 35 9 25 7 13 20 2 37 54 41 44 13 2 11
34 14 20 20 27 31 30 12 4 37 16 11 23 31 45 21 12
1 10 2 20 1 26 37 50 53 34 39 51 48 22 41 57 30
9 15 45 4 36 10 48 54 2 44 14 10 2 53 53 24 13
16 33 43 53 61 60 1 30 30 48 23 14 48 2 59 24 13

I will post the solution and key upon request.

II ___ =
_ _ _ _ /_ _ / _ _ _ / _ _ _ /_ /_ _ _ _

@ smokie: I’ll try it asap..nice to find a new cipher

UPDATE:

The first test run is complete. The run itself took about 40-50 hours of computation. However, we have now checked all (!) possibilites with the combination of the following settings

+ symbol: L
L symbol: A, E, I, O, U
IoFBc: "TIONS", "CTION"

on words with a length >5 (~ 2,000 dictionary entries).

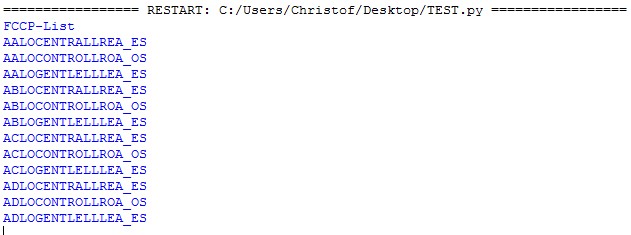
As a result, there is now a list with approximately 20,000 entries. These, however, appear to be grouped into certain words matching the criteria. Amongst those, there are entries such as:

ABLOCONTROLLROA_OS
ALLOCENTRALLREA_ES
BELONGNTEOLLEGB_GS
COLONYNTWULLWYC_YS
ADLIFSOCIALLISA_SN
BELIEFOCSILLSFB_FN
ONLINEOCXELLXEO_EN
POLICEOCPILLPEP_EN

For each word found there exists a group of 20 to 5,000 comparable text strings.

Obviously, additional words can now be found in accordance with both, the cipher structure and the settings (e.g. frequency expectation of ‘IoFBc’ or the letter ‘L’ as representing the + symbol). The list can be used for further analysis, e.g. finding a second word.

A total of 118,813,760 potential text combinations (considering the settings above) has thus now been reduced to approximately 20,000 potential cleartext phrases only. Thus, the elimination quota of ‘nonsense’ text strings has been 99.9974% (or approximately 6,000:1). IMO this is a nice method to get closer to the cleartext of the cipher.

So far, none of the results appear to consist of any complete logical text, however. This may have different reasons:

– no word with a length >5 in the phrase
– word >5 does exist. however is not present in the dictionary
– + symbol is a different letter than ‘L’ (79% unlikely, but still possible)
– ‘IoFBc’ 5-gram is different than the 5-grams considered above (most likely the case)
– solution is there, but hasn’t been found inside the 20,000 results

Potential improvements:

1. Extended range of 5-grams
2. Improved computation method (e.g. would a >10 Tflop machine still take approximately 5 minutes to perform the calculation..)
3. Implementation of an algorithm for better lexical analysis (e.g. Aho-Corasick)
4. Alternative settings (larger dictionary etc.)

Next step is to get get a bit deeper into the Aho-Corasick issue…this should somehow lead to improved results: Only a few or even only one single result instead of 20,000. However the algorithm might come with additional problems: Words such as I, A, AM, BE etc. could possibly be found in a variety of results, e.g. IAMBEHOWASIF etc..

We’ll see what will work best. If you have any ideas to improve, especially regarding the lexical analysis, lease let me know.

QT

Success..step by step. The tool is now working, so we can find multiple words in our text strings. It looks similar to this one:

..
__LOCENTRALLRE__ES
[{'index': 4, 'word': 'central'}]

__LOCONTROLLRO__OS
[{'index': 4, 'word': 'control'}, {'index': 4, 'word': 'control'}]

__LOGENTLELLLE__ES
[{'index': 4, 'word': 'gentle'}, {'index': 4, 'word': 'gentle'}, {'index': 4, 'word': 'gentle'}]
..

One thing still to do is to delete the double/triple etc. entries regarding the words found.

BUT: The tool is able to find multiple words inside a string and it does use the Aho-Corasick algorithm . This is quite interesting if we consider the string to be of length =18, which would generally include at least 3-5 words..selecting the strings with at least three words in it should then deliver us the cleartext solution.

If we can solve the final problem mentioned above, the program may run through multiple possibilities (for a year if it is necessary..) and will spit us all the text strings containing multiple words out..for each constellation desired (ngrams, + symbol etc..as we like).

The bad news is that I still believe we need a faster computer… (both computational efforts…creating the text strings and comparing the dictionary via Aho-Corasick).

QT

The FCCP analyzer is running..

1. Setting up a variety of strings consisting of variables complying to the 340 cipher’s structure, e.g. ordered by frequency of n-grams (FCCPs)
2. Aho-Corasick-Algorithm for an improved multi-pattern (dictionary word) search function
3. Returning all strings with e.g. at least two words found as a list

..it is therefore..

a.) searching for multiple words
b.) considering the cipher’s structure and specific frequencies (e.g. trigrams)
c.) returning potential cleartext results

..and is doing all this automatically

Some more comments:

– So far, the results are ‘overlapping’, which is necessary as non-overlapping results would require a full dictionary including 1-letter words (currently >3) which might contort our finding at least two words (with sense).
– Aho-Corasick algorithm is not very much faster than any [any (for x in string for x in lex)} function, imo
– Serious overlapping may still be avoided by dictionary modification (e.g. ‘sell’ but no ‘sells’ in it)
– Python is incredibly slow

This runs specifically considers a string of length = 12. The good part of it, however, is that with a faster computation this tool is able to select e.g. all varieties of minimum 5 words in a string of 18 letters (!). Although due to the iteration of variables this would still be a list, one may expect that – sooner or later – the cleartext solution is produced into that list. And, instead of trying zillions of varieties, the FCCP analyzer delivers all potential cleartext phrases without asking how many calculations still follow. Best results due to frequency tables. If the cleartext can’t be found on that list (e.g. because it is too long), a computational cross-comparison of results from other areas of the cipher would still work.

Give me a faster computer and Z won’t be crackproof anymore.
(Hope he’s reading this: It’s your last chance to confess..)

Update:

Here’s an update that shows how it works..first I’ve reduced ‘sells’ from the dictionay to ‘sell’. And we’ve got already two nice cleartext solutions (for this short phrase only):

LEEARTHALLHA – ‘..whole earth. All had..’
LETARTSELLSA – ‘..let art sell sandwiches..’

which could, in fact, already be part of the solution (I have to admit that ‘art’ had actually been searched as ‘arts’, same with all/hall…also this string is probably too short to analyze). Nevertheless..it’s two words found in a string of 12.

The set-up is currently with three A-Z variables, a list of (statistically) selected 5-grams plus one AEIOU, vowel variable. With 9 instead of 3 A-Z variables, on a very fast computer, it is possible to create a string of length = 24 (!) under the same conditions. Would be interesting to look into those to find multiple words (the string starting from the second letter in line 17 of the 340).

UPDATE II:

Another – huge – step forward: Today I modified the programmed code in a way that the so-called ‘trie’, the dictionary tree for the Aho-Corasick search algorithm, is not created for every single text string (taking ~1-2 seconds each ) but is now given as a constant in advance of the decryption process itself (text string creation & word analysis).

The result is astonishing: To check through 5,272,800 variations (considering frequencies and cipher structure simutaneously), took approximately two minutes only. That means it is possible to check out almost 4 billion variations in 24 hours only. With the correct set-up, the cleartext – if amongst those – will definitely show up amongst the results.

Out of the 5,272,800 variations, the tool was able to find 19,606 text strings with two words of length >4 letters inside. Expanding the 12-letter string and eventually combining it with other parts of the cipher, should lead to a final result. Due to the massively increased speed of the 63kb program, it now is possible to eliminate – in that specific run – 98.88% of all those variations that do not contain at least two words >4 letters.

Further analysis will be done, e.g. searching for three words, longer text string, cross-checking various parts of the cipher.

QT